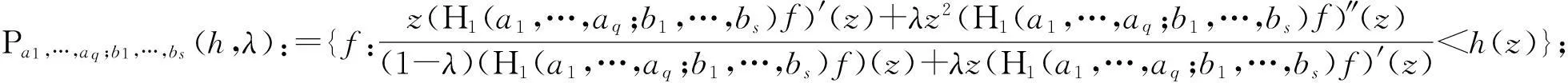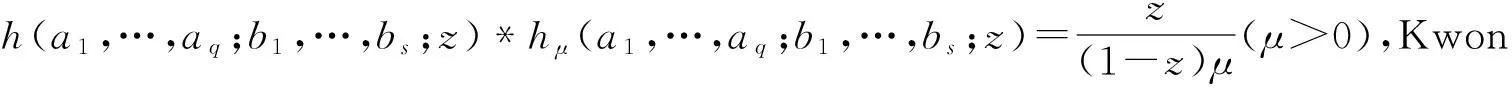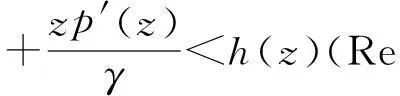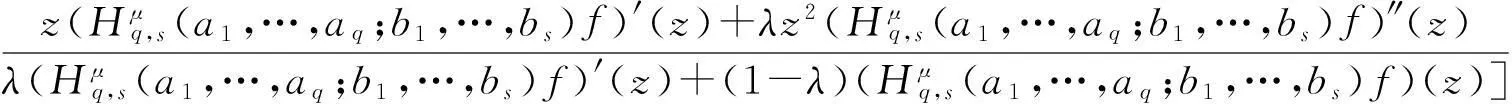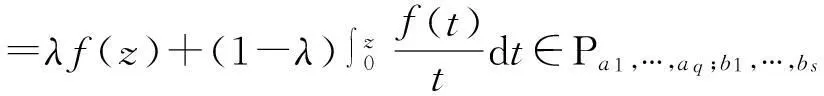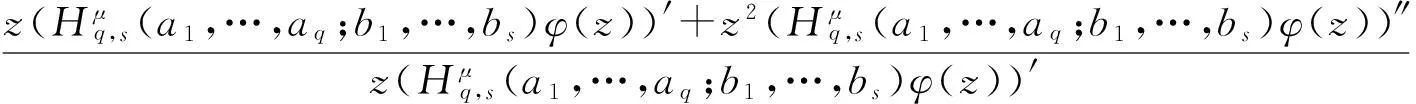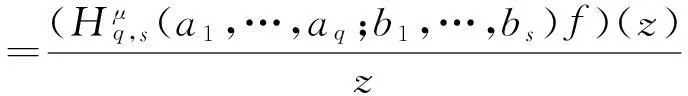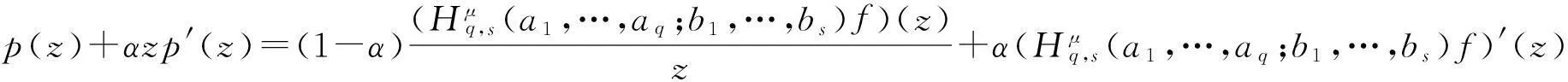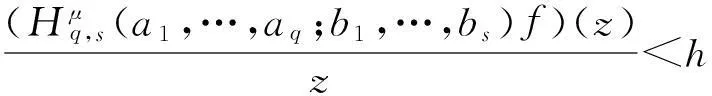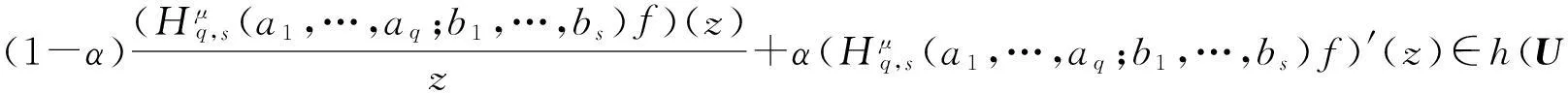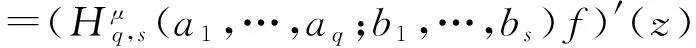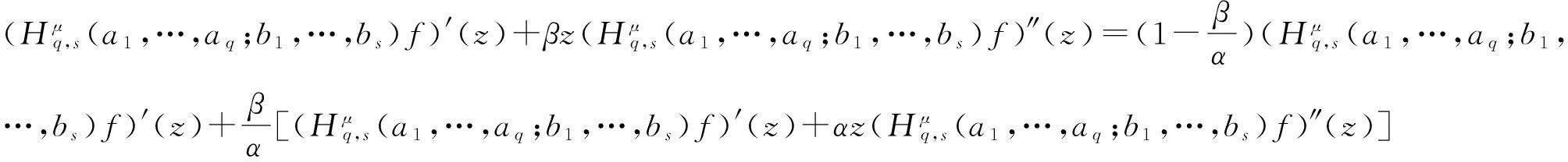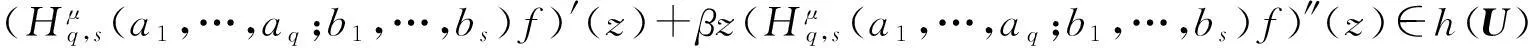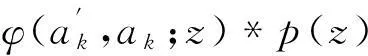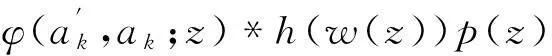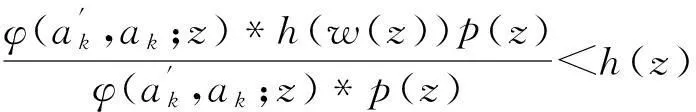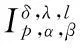由微分从属和卷积定义的解析函数类的包含性质

都俊杰，秦　川，邹发伟，李小飞

(1.长江大学工程技术学院，中国 荆州　434020; 2.长江大学信息与数学学院，中国 荆州　434000;3.澳门大学科技学院，中国 澳门　519040)



由微分从属和卷积定义的解析函数类的包含性质

都俊杰1*，秦川1，邹发伟1，李小飞2,3

(1.长江大学工程技术学院，中国 荆州434020; 2.长江大学信息与数学学院，中国 荆州434000;3.澳门大学科技学院，中国 澳门519040)

摘要本文由微分从属和卷积定义了在单位圆盘U={z∈C:|z|<1}内的三类单叶解析函数类Pa1,…,aq;b1,…,bs(μ,h,λ),Ta1,…,aq;b1,…,bs(μ,h,α),Ra1,…,aq;b1,…,bs(μ,h,α),并利用从属性质和凸函数的理论，研究得到了它们的包含关系.

关键词从属；卷积；包含性质；星象函数；凸函数

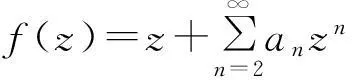
记N表示由单位圆盘U内的单叶解析凸的函数h(z)组成的正实部函数类，即满足Re{h(z)}>0.Ozkan和Altintas[1]定义了下面的函数类:

Ra(h,α):={f:(ka*f)′(z)+αz(ka*f)″(z)

Ra,c(h,α):={f:(L(a,c)f)′(z)+αz(L(a,c)f)″(z)

Ra1,…,aq;b1,…,bs(h,α):={f:(H1(a1,…,aq;b1,…,bs)f)′(z)+αz(H1(a1,…,aq;b1,…,bs)f)″(z)

z(hμ(a1,…,aq;b1,…,bs;z)*f(z))′=hμ(a1,…,aq;b1,…,bs;z)*zf′(z),

(1)

hμ(a1,…,aq;b1,…,bs;z)*z2f″(z)=z2(Hμq,s(a1,…,aq;b1,…,bs)f)″(z).

(2)

h(z),f∈A,z∈U},0≤λ≤1;h∈N;

(3)

h(z),f∈A,z∈U},α≥0;h∈N;

(4)

h(z),f∈A,z∈U},α≥0;h∈N.

(5)

本文利用从属性质与凸函数的理论，研究得到上述函数类的包含性质.

1基本引理

引理2[12]设0<α≤β,若β≥2或α+β≥3,则

引理3[13]若f(z)∈K,g(z)∈S*,则对于U内任意解析函数h(z),都有

2主要结论

定理1设g(z)=λzf′(z)+(1-λ)f(z),则f(z)∈Pa1,…,aq;b1,…,bs(μ,h,λ)当且仅当g(z)∈Pa1,…,aq;b1,…,bs(μ,h,0).

证利用(1)、(2)式，得

因此，g(z)∈Pa1,…,aq;b1,…,bs(μ,h,0).反过来，若g(z)∈Pa1,…,aq;b1,…,bs(μ,h,0),按同样的方法容易得到f(z)∈Pa1,…,aq;b1,…,bs(μ,h,λ).

证设f(z)∈Pa1,…,aq;b1,…,bs(μ,h,λ),zφ′(z)=λzf′(z)+(1-λ)f(z)=g(z),由于g(z)∈Pa1,…,aq;b1,…,bs(μ,h,0),故zφ′(z)∈Pa1,…,aq;b1,…,bs(μ,h,0).经计算，得

因此，φ(z)=Pa1,…,aq;b1,…,bs(μ,h,1).

定理3若f(z)∈Ta1,…,aq;b1,…,bs(μ,h,α),则f(z)∈Ta1,…,aq;b1,…,bs(μ,h,0).

定理4若α>β≥0,f(z)∈Ta1,…,aq;b1,…,bs(μ,h,α),则f(z)∈Ta1,…,aq;b1,…,bs(μ,h,β).

证当β=0时，由定理3容易得到结论.当β>0时，设f(z)∈Ta1,…,aq;b1,…,bs(μ,h,α),由函数类的定义和从属性质知

故f(z)∈Ta1,…,aq;b1,…,bs(μ,h,β).

定理5若f(z)∈Ra1,…,aq;b1,…,bs(μ,h,α),则f(z)∈Ra1,…,aq;b1,…,bs(μ,h,0).

定理6若α>β≥0,f(z)∈Ra1,…,aq;b1,…,bs(μ,h,α),则f(z)∈Ra1,…,aq;b1,…,bs(μ,h,β).

证当β=0时，由定理5容易得到结论.当β>0时，设f(z)∈Ra1,…,aq;b1,…,bs(μ,h,α),由函数类的定义和从属性质知

故f(z)∈Ra1,…,aq;b1,…,bs(μ,h,β).

定理7f(z)∈Ra1,…,aq;b1,…,bs(μ,h,α)⟺zf′(z)∈Ta1,…,aq;b1,…,bs(μ,h,α),

(6)

Ra1,…,aq;b1,…,bs(μ,h,α)⊂Ta1,…,aq;b1,…,bs(μ,h,α).

(7)

证由函数类的定义和式(5)、(6)并经计算得

上式意味着式(6)成立.设f(z)∈Ra1,…,aq;b1,…,bs(μ,h,α),并令

证设f(z)∈Pa1,…,aq;b1,…,bs(μ,h,λ),则存在Schwarz函数w(z)使得

h(w(z)).

即f(z)∈Pa1,…,aq;b1,…,bs(μ,h,λ).

参考文献：

[1]OZKAN O, ALTNTAS O. Applications of differential subordination [J]. Appl Math Lett, 2006,19(3):728-734.

[2]TROJNAR-SPELINA L. On certain applications of the Hadamard product [J]. Appl Math Comput, 2008, 199(4):653-662.

[3]EL-ASHWAH R M, AOUF M K, ABD-ELTWAB A M. On certain classes ofp-valent functions invoving Dziok-Srivastava operator [J]. Acta Univ Apulensis, 2013,35(2):203-210.

[4]XU Q H, XIAO H G, SRIVASTAVA H M. Some applications of differential subordination and the Dziok-Srivastava convolution operator [J]. Appl Math Comput, 2014, 230(3):496-508.

[5]SEOUDY T M, AOUF M K. Inclusion properties for some subclasses of analytic functions associated with generalized integral operator [J]. J Egypt Math Soc, 2013,21(3):11-15.

[6]KWON O S, CHO N E. Inclusion properties for certain subclasses of analytic functions associated with the Dziok-Srivastava operator [J]. J Inequal Appl, 2007，35(4):1-10.

[7]刘竟成，张学军.Cn中单位球上Bergman型空间的一种积分算子[J].数学年刊A辑， 2013,34(3):257-268.

[8]李小飞，严证.某类积分算子解析函数的性质[J].湖南师范大学自然科学学报, 2013,36(4):11-15.

[9]田琳，韩红伟.算子解析函数的系数不等式[J].数学的实践与认识, 2014，44(18)：239-245.

[11]MILLER S S, MOCANU P T. Differential subordinations: theory and applications, series on monographs and textbooks in pure and applied mathematics [M]. New York: Marcel Dekker Incorporation, 2000.

[12]RUSCHEWEYH S. Convolutions in geometric function theory [M]. Montreal: Les Presses de l’Universite de Montreal, 1982.

[13]RUSCHEWEYH S, SHEIL-SMALL T. Hadamard product of schlicht functions and the polya-schoenberg conjecture [J].Comment Math Helv, 1973,48(4):119-135.

(编辑HWJ)

Inclusion Properties for Subclasses of Analytic Functions Defined by Differential Subordination and Convolution

DUJun-jie1*,QINChuan1,ZOUFa-wei1,LIXiao-fei2,3

(1.College of Engineering and Technology, Yangtze University, Jingzhou 434020, China;2.School of Information and Mathematics, Yangtze University, Jingzhou 434020, China;3.College of Science and Technology, University of Macau, Macau, 519040, China)

AbstractIn this article, we define three subclasses of analytic functions Pa1,…,aq;b1,…,bs(μ,h,λ),Ta1,…,aq;b1,…,bs(μ,h,α),Ra1,…,aq;b1,…,bs(μ,h,α) by using of differential subordination and convolution in the open disc U={z∈C:|z|<1}. Inclusion properties of these subclasses are obtained by employing properties of subordination and theories of convex functions.

Key wordssubordination; convolution; inclusion properties; starlike function; convex function

中图分类号O174.51

文献标识码A

文章编号1000-2537(2016)02-0077-05

*通讯作者,E-mail：29149875@qq.com

基金项目：湖北省自然科学基金资助项目(2013CFAO053);湖北省教育厅科研基金资助项目(B2013281)；长江大学科研基金资助项目(2013cjy01);长江大学工程技术学院科技创新基金资助项目(2015J0802)

收稿日期：2015-11-12

DOI:10.7612/j.issn.1000-2537.2016.02.013