钢桥面板U肋对接焊缝疲劳寿命研究*
王益逊 傅中秋 孙 童 徐 捷 朱 伟
(河海大学土木与交通学院1) 南京 210098) (安徽省招标集团股份有限公司 造价咨询部2) 合肥 230051)
钢桥面板U肋对接焊缝疲劳寿命研究*
王益逊1)傅中秋1)孙童1)徐捷1)朱伟1,2)
(河海大学土木与交通学院1)南京210098)(安徽省招标集团股份有限公司 造价咨询部2)合肥230051)
摘要:以江阴长江大桥为研究对象,建立正交异性钢桥面板局部有限元模型,计算各种标准疲劳车作用下U肋对接焊缝处的疲劳应力幅,结合BS5400规范得到该细节相应位置的疲劳损伤度;建立车辆轮迹分布模型,将影响疲劳损伤的各参数矩阵化,根据实桥车流模拟结果,提出一种考虑轮迹改变的疲劳损伤计算方法.结果表明,U肋对接焊缝腹板处的损伤相对较小,靠近顶板部位、腹板与底板交接部位,以及U肋底部的损伤较为严重;考虑车辆轮迹改变后的疲劳寿命与实测结果吻合度较高,因此考虑车辆轮迹位置的改变可以提高寿命评估的精确度.
关键词:车辆轮迹;钢桥面板;U肋对接焊缝;应力幅;损伤度;疲劳寿命
0引言
正交异性钢桥面板因为结构自重小、受力性能好、施工速度快、承载能力大等优点而获得广泛应用[1-3].根据实际工程调研结果,正交异性钢桥面板由于长期直接承受车辆荷载,疲劳损伤问题愈发严重,导致结构的耐久性和安全性受到削弱,某些情况下会引发桥梁倒塌事故.钢桥面板易开裂的原因主要是纵横加劲肋交叉多,构造复杂,在车轮荷载作用下容易在焊缝处产生集中应力,引起焊缝疲劳开裂[4].由于U肋在桥面体系中受力关键,发挥着纵梁的作用,如果出现疲劳失效,定然会威胁结构的整体安全,而U肋对接焊缝又是容易产生疲劳损伤的部位,因此开展U肋对接焊缝疲劳性能研究尤为重要.
钢桥面板局部疲劳寿命评估方式有实测疲劳寿命评估和有限元疲劳寿命评估.前者较为准确,但需要花费较大的人力物力,且实测过程中受环境干扰性较大;后者较为方便,但由于未考虑车辆轮迹改变的因素,结果往往偏保守.因此,有必要研究一种考虑车辆轮迹改变的有限元疲劳寿命评估方法.
文中以江阴长江大桥为研究对象,建立正交异性钢桥面板局部有限元模型,首先计算各种标准疲劳车作用下U肋对接焊缝处的疲劳应力幅,结合BS5400规范得到了该细节相应位置的疲劳损伤度;然后建立车辆轮迹分布模型,利用矩阵运算理论,将影响疲劳损伤的各参数矩阵化,根据实桥车流模拟结果,提出一种考虑轮迹改变的疲劳损伤计算方法.
1有限元分析模型
首先建立江阴长江大桥桥面板局部有限元模型,分析车轮荷载横向分布对正交异性钢桥面板构造细节疲劳应力幅的影响,模型见图1.顺桥向间距为4个横隔板间距,横桥向间距为7个U肋宽度.取U肋腹板尺寸为300 mm×6 mm×280 mm,钢桥面板厚度为12 mm,横隔板间距取为3.2 m ,U肋间距为300 mm,拟采用shell63单元进行模拟,钢的弹性模量取为206 GPa,泊松比取为0.3.模型加载工况与测点见图2.图中,e为车辆轮迹中线与待测U肋中心的横向距离,以150 mm作为一个加载工况,在一个车道长度范围内加载,共26个工况,考虑到对称性现仅计算13个工况,用以分析车辆轮迹分布对开裂前U肋对接焊缝疲劳的影响.

图1 模型示意图
在实桥监测过程中,发现U肋对接焊缝处的疲劳裂纹分布位置差异性较大,虽然大部分产生在U肋底板,但U肋腹板靠近顶板的位置也是一重要的裂纹源,因此有必要分析整个U肋对接焊缝的损伤分布情况.现分别布置C1(U肋腹板靠近顶板处)、C2(U肋腹板中间位置)、C3(U肋底板与腹板交接位置)、C4(U肋底部中间位置)四个测点进行整个U肋对接焊缝处损伤分布研究.

图2 加载工况与测点示意图
2标准疲劳车损伤度
2.1车辆荷载模型
根据文献[5],统计江阴长江大桥的8月份实际交通流量,见表1.

表1 2009年8月北网等效车辆模型轴重表 kg
根据统计结果,按照疲劳损伤等效原理,求出每一种模型车辆中各个轴的等效轴重,各个等效轴重之和为模型车辆的等效总重.货车等效轴重的计算公式为:
(1)
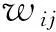
最终得到的车辆荷载模型见表2.
2.2标准疲劳车应力历程分析
根据江阴长江大桥实测应变历程数据,获得各标准疲劳车作用下U肋对接焊缝的应力历程曲线.现以二轴车为例,根据车辆荷载模型,前轴与后轴之间的距离为5.5 m,前轴轴重与后轴轴重分别为30,55 kN.各工况作用下各测点的应力历程曲线见图3.
综合各测点的疲劳在各轴车作用下的应力变化曲线,各轴车的应力变化规律如下.
1) 各轴车作用下,测点C2,C3,C4应力变化规律相同,当车轮离焊缝位置较远时,该细节主要承受较小的拉应力,随着车辆的移动,该细节逐渐由拉应力变为压应力,车辆行驶至焊缝正上方时,该细节处的应力急剧增大,并由压应力转换为较大拉应力,车辆驶离焊缝时,该细节的疲劳应力又会继续减小并变化为压应力.

表2 江阴大桥等效车辆荷载模型

图3 二轴车作用下各测点应力变化曲线(e单位:mm)
2) 各轴车作用下,测点C1与C2,C3,C4应力变化规律相反,当车轮经过该细节时,该测点主要表现为压应力,这主要是由于车轮作用下,U肋腹板、顶板相互约束,使得U肋腹板与顶板部位局部受压,该部位的应力分布见图5.
3) 各轴车作用下,U肋对接焊缝处所产生多个应力峰值数与车轴数对应,且较重的车轴会产生较大的应力峰值.
4) 各轴车作用下,U肋对接焊缝处的应力对车轮位置较为敏感,随着车辆位置横向偏移量增大,相同轮载作用下所产生的疲劳应力逐渐减小.

图4 U肋对接焊缝顶板处横向应力分布
2.3标准疲劳车损伤度计算
为了更加直观的分析箱梁局部区域在不同车轮位置作用下的损伤差异,基于上述计算结果,根据Miner线性累积损伤理论[5-6]计算不同车辆位置作用下U肋对接焊缝各部位的标准损伤度.即
(2)
式中:ni为第i个应力幅的循环数;Ni为对应于第i个应力幅的疲劳失效寿命.根据英国桥梁规范BS5400中对于σr-N(S-N)关系规定进行计算,即
(3)
式中:N为在应力幅σr作用下构件发生破坏所需要的次数;参数K0,Δ,m可根据构造细部的疲劳等级由规范得到;d为概率因子,取d=2,对应失效概率为2.3%.
对于低于疲劳极限σ0的σr,根据BS5400规范中“低值应力循环的处理”方法,按下式处理.
(4)
综合各测点的疲劳在各轴车作用下的疲劳损伤度,各轴车作用下的疲劳损伤度变化规律如下.
1) 各标准疲劳车作用下,随着车辆位置横向偏移量增大,相同轮载作用下所产生的疲劳损伤度逐渐减小,且呈先急剧下降后趋于平稳的趋势.对于各标准疲劳车作用下的相同测点,当偏心距大于750 mm的时,标准疲劳车作用下的疲劳损伤度比偏心距为0 mm时的疲劳损伤度降低均大于99%,表明当偏心距大于750 mm时,车辆荷载对疲劳细节的寿命基本没有影响.
2) 各标准疲劳车作用下,随着标准疲劳车轴重的增加,对U肋对接焊缝处的疲劳损伤也逐渐增加,如二轴车作用下C4测点的疲劳损伤度为2.860 29×10-8,六轴车作用下C4测点的最大疲劳损伤度为7.145 94×10-7,为二轴车的24.9倍,因此,实桥应加强对重车以及超载车辆的管理,重车的疲劳所引起的疲劳损伤往往是轻车的几十倍.
3) U肋对接焊缝处的疲劳损伤分布差异较大,计算结果显示,U肋对接焊缝靠近顶板部位、以及腹板与底板交接部位以及U肋底部的损伤较为严重,而U肋对接焊缝腹板处的损伤相对较小,如六轴车作用下,e=600 mm时,计算结果显示,C1部位的疲劳损伤度1.005 39×10-8,C2部位的疲劳损伤度为1.140 58×10-14,C3部位的疲劳损伤度为5.944 28×10-12,C4部位疲劳损伤度为7.525 81×10-13,C1部位的疲劳损伤度约为C2部位的8.86×105倍.
3车轮分布模型及考虑轮迹改变的疲劳损伤评估方法
3.1车轮分布模型
根据国内外车轮分布模型的研究成果[7-9],现针对江阴长江大桥做如下假定:(1)江阴长江大桥各车道随机车流的相互独立;(2)江阴长江大桥各车道随机车流的车轮分布位置服从正态分布.
此时,江阴长江大桥的车轮分布模型为
(5)
根据以上假定,将该车轮分布模型沿着车道宽度积分(江阴长江大桥车道宽度3.75 m).
(6)
求得σ=539,则最终江阴长江大桥的建议车轮分布模型为
(7)
车辆在路面上行驶时,车道具有一定的宽度,见图5,轮迹的横向分布是不均匀的,实际上车辆轮迹仅具有一定宽度,车辆通过时只能覆盖小部分.因此,车轮经过不同位置所产生的概率是不同的.为了得到江阴长江大桥车道各部分的车轮分布情况,现将该模型进行分段(沿着车轮的宽度)积分,获得车道各部分的随机车流概率分布,见图6.

图5 车道分段示意图

图6 车辆概率分布
3.2考虑轮迹改变的疲劳损伤评估方法
根据计算结果,再将整个车道每一部分的概率分布转化成1×13的车轮横向分布概率矩阵μ,以车道位置为“行”,以概率为“列”.即
(8)
根据2计算结果,以车辆类型为“行”,以车道横向分布位置为“列”,将5种疲劳车的标准疲劳损伤度转化为5×13的损伤度矩阵w.
将损伤度矩阵与横向分布位置矩阵相乘即为损伤矩阵S,再将损伤矩阵各项相加即为该疲劳细节在车流作用下的疲劳损伤度U.
公式表达为
(9)
(10)
式中:U为总损伤度;w为损伤矩阵;μ为分布概率矩阵.
4U肋对接焊缝疲劳寿命评估
4.1实桥车流模拟
本文所使用的行驶模型为以泊松分布原理的断面[10]发车模型,以车辆之间的时间间隔为随机变量,并作如下假定:(1)在不相重叠的时间区间内车辆的产生是互相独立的;(2)对充分小的Δt,在时问区间[t,t+Δt]内有一辆车产生的概率与t无关,而与区间长度Δt成正比,即车辆的产生具有平稳性;(3)对于充分小的Δt,在时间区间[t,t+Δt]内一条车道上有2辆或2辆以上车辆产生的概率极小.
(11)
式中:P(k)为在计数间隔t内到达k辆车的概率;λ为单位间隔时间的平均到达率,辆/s;t为每个计数间隔持续的时间或距离.
车流随机模拟结果见图8.

图7 车道随机车流模拟
由图7可知,其中类型2~6表示不同轴数的货车,类型1表示轿车、小型客车,对桥梁疲劳损伤影响较小.在快车道主要以2轴车与客车居多,多轴数的货车数量较少,慢车道则以多轴数的货车为主.根据实测车流结果,该车流模拟结果与实桥车流情况相符.因此利用该车流模拟结果进行疲劳损伤分析是可行的.
现根据车流模拟结果,各种类型车辆的数量建立13×1车流矩阵Q,以车辆类型为矩阵的“行”,以各类型车辆的数量为“列”.
4.2考虑轮迹改变的疲劳寿命计算
根据2.1各工况作用下U肋对接焊缝处的标准疲劳损伤度、3.2考虑轮迹改变的疲劳损伤计算方法,以及4.1随机车流模拟结果,该部位一段时间内的疲劳损伤度最终为
(12)
式中:U为总损伤度;W为损伤矩阵;Q为车流矩阵; μ为分布概率矩阵.
再将疲劳损伤疲劳转化为疲劳寿命(年),见表3.

表3 考虑轮迹改变的疲劳寿命
通过与文献[11]实测疲劳寿命对比,发现考虑车辆轮迹改变后的U肋对接焊缝疲劳寿命与实测结果吻合度较高,如快车道相同位置(U肋对接焊缝底板中部)处实测结果为471 a,考虑轮迹改变后的寿命计算结果为447 a,而不考虑轮迹改变的计算结果为152 a.因此在疲劳寿命计算中考虑车辆轮迹位置的改变可以提高寿命评估的精确度.
5结论
1) 对于各标准疲劳车作用下的相同测点,当偏心距大于750 mm的时,标准疲劳车作用下的疲劳损伤度比偏心距为0 mm时的疲劳损伤度降低均大于99%,表明当偏心距大于750 mm时,车辆荷载对疲劳细节的寿命基本没有影响.
2) U肋对接焊缝处的疲劳损伤分布差异较大,计算结果显示,U肋腹板处的损伤相对较小,U肋对接焊缝靠近顶板部位、腹板与底板交接部位以及U肋底部的损伤较为严重,该三处疲劳细节需要给予足够的重视.
3) 通过与实测疲劳寿命对比,发现考虑车辆轮迹改变后的U肋对接焊缝疲劳寿命与实测结果吻合度较高.因此在疲劳寿命计算中考虑车辆轮迹位置的改变可以提高寿命评估的精确度.
参 考 文 献
[1]吉伯海,田圆,傅中秋,等.正交异性钢桥面板横隔板切口疲劳应力幅分析[J]. 工业建筑,2014(5):128-131,153.
[2]王春生,冯亚成.正交异性钢桥面板的疲劳研究综述[J].钢结构,2009(9):10-13+32.
[3]蒲黔辉,高立强,刘振标,等.基于热点应力法的正交异性钢桥面板疲劳验算[J]. 西南交通大学学报,2013(3):395-401

[5]吕磊,吉伯海,马麟,等.基于实测车流的大跨度悬索桥振动响应研究[J].土木工程学报, 2011,44(S):102-108.
[6]崔闯,卜一之,张清华,等.基于热点应力法的正交异性钢桥面板疲劳寿命评估[J].桥梁建设,2014(4):62-67.
[7]潘鹏,李全旺,周怡斌,等.某公路大桥车辆荷载调查与局部疲劳分析[J].土木工程学报,2011,44(5):94-100.
[8]刘黎萍,孙立军.高速公路不同车道车型组成分析[J].中外公路,2004,24(1):48-51.
[9]李星新.基于健康监测的钢桥面板疲劳寿命评估[D].长沙:中南大学,2012.
[10]莫智锋,余嘉,孙跃.基于泊松分布的微观交通仿真断面发车数学模型研究[J].武汉理工大学学报(交通科学与工程版),2003,27(1):73-76.
[11]吉伯海,朱伟,傅中秋,等.正交异性钢桥面板U肋对接焊缝疲劳寿命评估[J].重庆交通大学学报(自然科学版),2015(1):16-21.
Fatigue Life Study of U-rib Butt Weld of Steel Bridge Deck
WANG Yixun1)FU Zhongqiu1)SUN Tong1)XU Jie1)ZHU Wei1,2)
(CollegeofCivilandTransportationEngineering,HohaiUniversity,Nanjing210098,China)1)
(CostConsultancyDepartment,AnhuiTenderingGroupInc.,Hefei230051,China)2)
Abstract:The Jiangyin Yangtze River Bridge is studied in this paper. The local finite element model of orthotropic steel bridge deck is established. The fatigue stress amplitude of U-rib butt weld under all kinds of standard vehicle loads is calculated and thus the fatigue damage degree of a certain position is obtained according to the specification BS5400. Then, the vehicle wheelmark distribution model is built up. By matrixing all parameters that affect the fatigue damage and considering wheelmark changes, a fatigue damage calculation method is proposed based on the simulation results of traffic flow. The results show that the damage of U-rib web butt weld is relatively less while that near the roof, of web-floor joint and of U-rib floor is more serious. In addition, the fatigue life of U-rib butt weld by considering wheelmark changes matches well with the measured results. Therefore, the accuracy of fatigue assessment could be improved by considering wheelmark changes in the calculation of fatigue life.
Key words:wheelmark; steel bridge deck; U-rib butt weld; stress amplitude; damage degree; fatigue life
doi:10.3963/j.issn.2095-3844.2016.02.030
中图法分类号:TG405
收稿日期:2016-02-14
王益逊(1994- ):男,硕士,主要研究领域为桥梁与隧道工程
*国家自然科学基金面上项目(51478163)、高等学校博士学科点专项科研基金(20120094110009)、江苏省交通科学研究计划项目(2014Y02)资助

