基于拓展Kalman滤波的船舶自由横摇参数辨识*

霍　聪　董文才

(海军工程大学舰船工程系　武汉　430033)



基于拓展Kalman滤波的船舶自由横摇参数辨识*

霍聪董文才

(海军工程大学舰船工程系武汉430033)

摘要：提出一种基于拓展Kalman滤波的船舶自由横摇辨识算法，可以对横摇阻尼及回复力系数进行参数辨识.该算法可使用横摇角位移、角速度、角加速度信号或者它们的组合作为辨识输入.通过对非线性横摇的仿真运动进行辨识，确定了有效参数初值的选取范围，同时发现即使在观测误差较大时该算法仍能获得较精确的辨识结果，且减小测量误差,有助于提高辨识精度.在确定了适用于目标船模的阻尼模型后，根据试验数据,辨识其自由横摇参数并以此进行横摇运动仿真，所获得的仿真曲线与试验测量值匹配良好.

关键词：自由横摇；参数辨识；拓展Kalman滤波

0引言

可靠的横摇阻尼估计是准确预报船舶在波浪中横摇运动的重要条件，当波浪频率接近船的固有频率时船体将产生大幅横摇，此时由于摩擦阻力、涡流阻力、兴波阻力等作用的存在，横摇阻尼受粘性影响显著且回复力非线性开始显现，横摇阻尼的预报方法必须有效计及这些因素的影响.自由横摇试验是获取船舶在固有频率下横摇运动参数的一种有效途径，充分高效地提取、处理和利用自由横摇数据则是获取横摇阻尼及回复力的关键.

根据船舶横摇运动数学模型描述方法的不同，船舶自由横摇阻尼的辨识方法可以分为参数化方法和非参数化方法.参数化方法通常是基于特定的横摇阻尼及回复力模型，根据指定的算法寻找满足目标函数最优的参数解，常用的减灭曲线法和能量法都属于参数化方法.减灭曲线法[1]利用自由横摇衰减曲线的峰值点作为能量的度量对横摇阻尼进行辨识，该方法所获得的横摇阻尼分布通常较为分散，因此在阻尼曲线拟合的过程中往往需要讨论阻尼模型的适用性.能量法则根据机械能守恒原理，通过引入能量函数并利用横摇角位移和角速度时历曲线对横摇阻尼模型的参数进行估计.Roberts[2]利用三次样条曲线拟合角位移的峰值点并基于最小二乘对横摇阻尼进行辨识，发现初始横摇角的测量精度对能量函数影响很大，直接关系到非线性阻尼模型的适用性.Bass等[3]基于能量法探讨了8种横摇阻尼模型的适用性，发现“平方”“立方”和“平方+线性角”阻尼模型的适用性较高.Wilson[4]、马山等[5]为了克服测量噪声对能量函数积分误差的影响，采用余弦衰减函数拟合横摇曲线从而获得高精度的同步横摇运动时历信号.针对常用的参数化方法在大幅横摇时出现辨识参数为“负值”的问题，Fernandes等[6]提出将横摇阻尼划分为大幅横摇和小幅横摇的双线性模型，但是尚需要讨论该模型对不同船型的适用性.Jang等[7]还提出了一种非参数化的方法，通过引入Tikhonov正则化方程求解Volterra第一类积分直接获取横摇阻尼值.该非参数化方法虽然免去了引入阻尼模型假设的误差，但是由于所得横摇阻尼为离散化的散点，仍需要通过其他数学模型对阻尼离散点进行拟合，从而引入了新的误差.

本文提出一种新的船舶自由横摇参数化辨识方法，通过将待辨识参数作为状态变量，在时历点上采用拓展Kalman滤波原理进行递推得到参数的最小方差估计.此外，新引入了角加速度信号，可以单独或者同时采用角位移、角速度和角加速度信号作为辨识算法的输入，拓宽了横摇参数辨识输入的选取范围，并可实现辨识结果之间的相互佐证.

1横摇运动方程辨识算法

1.1运动模型

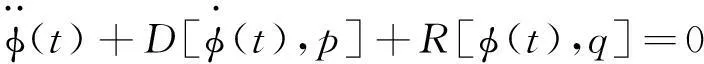
(1)

(2)

1.2状态方程

(3)

(4)

1.3观测方程

分别选取角位移、角速度和角加速度Yi[k](i=1,2,3)作为观测量时，相应的观测方程见式(5)～式(7).

式中：vi[k](i=1,2,3)分别代表均值为零的高斯观测误差，满足E[v·vT]=Rijδij，δij为Kroneker符号.当同时采用角位移、角速度和角加速度多个观测量进行辨识时，观测方程可扩展为式(8).

(7)

(8)

式中：Y[k]={Yi[k]}；H[k]={Hi[k]}；V[k]={Vi[k]}，i=1,2,3.

1.4状态参数辨识

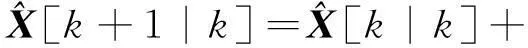
(9)

2辨识算法特性研究

船舶自由横摇运动的参数辨识是基于所建立的数学模型，借助观测结果对物理过程的特征参数进行揭示的过程，影响辨识精度的误差主要来源于测量误差和模型误差本身.

2.1辨识输入的观测组合

表1　自由横摇仿真参数值

表2　辨识输入的观测量组合形式

2.2参数辨识初值敏感性分析

1) 图1统计了所有初值组合的参数辨识误差，发现误差集中在非线性阻尼系数p2和p3，误差的绝对值最大可以达到25%.由此可见非线性阻尼系数的辨识精度对参数初值的变化较为敏感，参数初值的选取对辨识结果的正确性至关重要.

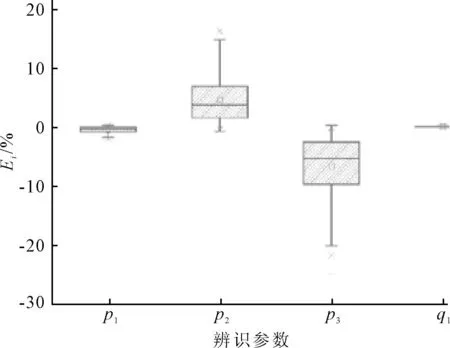
图1　辨识参数相对误差统计

2) 将所有对p2和p3的辨识误差小于5%的参数初值点单独分离出来，然后以这些点的线性阻尼系数p1int与回复力系数q1int的初值作平面分布如图2所示，发现这些点几乎均匀分布在整个线性参数初值的取值空间内.由此可知线性阻尼系数和回复力系数的初值选取对参数辨识结果没有决定性的影响.

图2　Ei<5%初值点的p1int-q1int分布

3) 进一步分析非线性阻尼系数p2,p3辨识误差的分布规律发现，如果以辨识误差的绝对值作高程，以非线性阻尼系数初值p2int和p3int为平面横纵坐标作云图见图3～4.图中横纵坐标均以相应参数的真值进行比例化.可见p2和p3的辨识误差随非线性阻尼系数初值的变化呈平面对角分布，当参数初值落于0到真值1.3倍的区间内时，辨识误差小于3%.因此，辨识时参数的初值通常可取一小值,如p1取10-5.

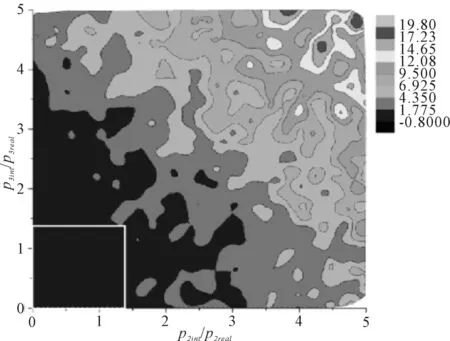
图3　p2辨识误差受初值影响

图4　p3辨识误差受初值影响

2.3测量误差对辨识的影响

表3　各观测量测量误差取值

3自由横摇试验参数辨识

以图5所示深V船型作为研究对象，模型的主要参数见表5,以水线长Lwl进行无因次化.针对目标船模开展初始横倾角为5°，10°，15°，20°的静水自由横摇试验，利用试验测量数据对横摇阻尼和回复力系数进行辨识，并以辨识所得参数进行横摇仿真，将仿真结果与试验测量时历曲线对比从而检验辨识的精度.

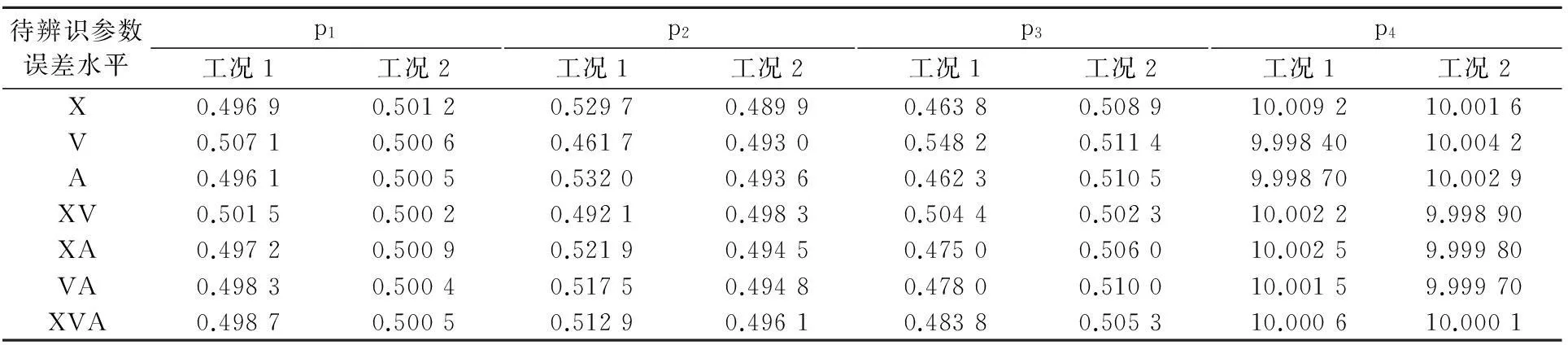
表4　不同测量误差下参数辨识结果

3.1横摇阻尼模型适用性

为获得准确的横摇参数估计，首先需要确定适合于目标船型的横摇阻尼模型.以横摇角位移作为辨识输入，分别采用平方阻尼(quadratic)和立方阻尼(cubic)模型进行参数辨识.Bass，Haddara认为可靠的阻尼模型应当在整个横摇角度范围内都具有良好的适用性.为此，根据不同阻尼模型的辨识结果计算横摇阻尼进行对比，结果见图6.在不同初始横倾角下，由平方阻尼模型所预报横摇阻尼的一致性较好，而采用立方模型所预报横摇阻尼在15°～20°大幅横摇时偏差较大.鉴于共振频率附近主要研究船舶的大幅横摇，因此对目标船型采用平方阻尼模型更加合适.

图5　深V型船体几何

表5　目标船模主要参数

图6　不同初始横倾角下横摇阻尼变化情况

3.2参数辨识仿真对比

图7　各种输入对3种横摇运动的辨识仿真(SI)精度对比

图8　横摇角位移曲线的辨识仿真与试验对比

图9　横摇角速度曲线的辨识仿真与试验对比

图10　横摇角加速度曲线的辨识仿真与试验对比

4结 束 语

文中提出一种可以兼容角位移、角速度和角加速度的船舶自由横摇参数辨识算法，研究表明：该算法对参数初值的选取具有较强的稳定性，可以适应观测量存在较大测量误差的情况，采用多种信号组合较单独采用某一种信号作为辨识输入可使参数辨识精度总体上有所提升.

参 考 文 献

[1]彭英声.舰船耐波性基础[M].北京:国防工业出版社,1989.

[2]ROBERTS J B. Estimation of nonlinear ship roll damping from free-decay data[J]. Journal of Ship Research, 1985,29(2):127-138.

[3]BASS D W,HADDARA M R. Nonlinear models of ship roll damping[J]. International Shipbuilding Progress, 1988,35(401):5-24.

[4]Wilson R V, Carrica P M.Unsteady RANS method for ship motions with application to roll for a surface combatant[J]. Computers & Fluids, 2006(35):501-524.

[5]马山,曹宇.基于能量法的船舶静水横摇试验阻尼估算方法研究[J].船舶力学,2010,16(10):1122-1130.

[6]FERNANDES A C, OLIVEIRA A C. The roll damping assessment via decay model testing (new ideas about an old subject)[J]. Journal of Marine Science and Technology, 2009(8):144-150.

[7]JANG T S,KWON S H.Recovering the functional form of the nonlinear roll damping of ships from a free-roll decay experiment: An inverse formulism[J]. Ocean Engineering, 2010,37:1337-1344.

[8]DALZELL J F. A note on the form of ship roll damping[J]. Journal of Ship Research, 1978,22(3):178-185.

[9]李培勇,冯铁城,裘泳铭.三体船横摇运动[J].中国造船，2003(1)：55-58.

[10]谢楠，VASSALOS V，LEE B S，等.带舭龙骨柱体的横摇阻尼的粘性流计算[J].船舶力学，2007(6)：43-48.

[11]纪东方,朱良生,JI Dongfang,等.黏性流中船舶自由横摇衰减运动数值模拟[J].科学技术与工程，2009(23)：24-28.

[12]张杰.集装箱船迎浪参数横摇的数值模拟方法研究[D].哈尔滨：哈尔滨工程大学，2014.

Identification of Ship Roll Parameters from Free-roll Decay Based on Extended Kalman Filtering

HUO CongDONG Wencai

(DepartmentofNavalArchitecture,NavalUniversityofEngineering,Wuhan430033,China)

Abstract：This paper proposes an identification method of ship roll parameters based on the extended Kalman filtering theory, which can be used to obtain the damping and restoring force coefficients of ship free-roll decay. Inputs to the identification algorithm can be widely chosen from signals including angle, angular velocity, angular acceleration or their combinations. The range of initial parameter value is determined through identification tests of nonlinear roll simulations. High identification accuracy can still be achieved with relatively big measurement errors and the reduction of measurement error is helpful to improving the identification accuracy. The free-roll decay simulation based on the parameters identified from ship model tests and proper damping model confirmed from model tests, shows good agreement with the experimental data.

Key words：free-roll decay; parameter identification; extended Kalman filtering

doi:10.3963/j.issn.2095-3844.2016.02.004

中图法分类号：U661.32

收稿日期：2016-01-18

霍聪(1989- )：男，博士生，主要研究领域为舰艇流体动力性能

*国家自然科学基金项目资助(50879090)