IRP理论和IEEE Std 1459-2010在变流器驱动电机能效测试中的应用比较

杨立敏, 李耀华, 王 平, 李子欣, 崔冬冬

(1. 中国科学院电工研究所大功率电力电子与直线驱动技术研究部， 北京 100190；2. 中国科学院大学， 北京 100049)

IRP理论和IEEE Std 1459-2010在变流器驱动电机能效测试中的应用比较

杨立敏1,2, 李耀华1, 王 平1, 李子欣1, 崔冬冬1,2

(1. 中国科学院电工研究所大功率电力电子与直线驱动技术研究部， 北京 100190；2. 中国科学院大学， 北京 100049)

由于变流器输出的非正弦电压电流波形具有多样性和复杂性，传统的功率理论在变流器驱动电机能效测试中已经失去实用性。本文将两种主流的非正弦条件下的功率理论，即瞬时无功功率理论(IRP)和标准IEEE Std 1459-2010，引入变流器驱动电机的能效测试中，对比分析其实用性。首先基于数学分析，提出了一种考虑铁耗的三相异步电机仿真模型，并以此构建了一个典型的两电平PWM变流器电机驱动系统。以此系统作为算例，通过利用IRP理论、标准IEEE Std 1459-2010中提供的方法以及电机仿真算例中的内部变量，对电机的有功功率、视在功率进行了对比。结果表明，在变流器驱动电机能效测试中，这两种理论对电机效率的评估效果相同，与通过仿真算例内部变量计算得到的效率相吻合；在视在功率评估上，采用标准IEEE Std 1459-2010更合适。

电机能效； 电机损耗仿真模型； 瞬时无功功率理论； IEEE Std 1459-2010

1 引言

在以电磁场能量守恒和基本电路原理为基础的电气系统功率理论中，单相正弦以及三相正弦平衡条件下的功率定义已经很完善，在工业生产生活实践中能够很好地解决所遇到的问题。而在非正弦和三相不平衡条件下传统的功率定义将失去其有效性。如今，随着电力电子装置在电机驱动和输配电领域的广泛应用，电气系统的非线性化日趋严重，文献[1]对此现状做了详细的阐述。

三相异步电机作为各种设备的动力来源，被广泛应用在各行各业中。据统计，2010年我国全社会耗电量达到4.19万亿kW·h，其中工业耗电量占约70%，电机系统耗电量则又占工业总耗电量的60%～70%[2]。因此，通过分析电机系统的能耗，为电机行业实现节能降耗是十分有意义的。在常用的异步电动机模型中，为方便控制分析，常常忽略电机的铁耗。但铁耗是真实的，研究表明[3]，在高硅钢片做铁心材料的大型电机中，其铁耗所占的比例约为铜耗的10%～20%；而在采用较普通硅钢片的小容量电机中，铁耗所占的比例可达铜耗的50%。显然，在电机损耗分析中，应该将铁耗考虑在内。目前，国内外的学者就三相异步电机的仿真模型做了很多研究[4-9]，这些模型能够说明电机内部的损耗情况，但是计算公式较为复杂，在要求快速性和精确性的系统级损耗仿真实践中较少用到。本文在上述文献的基础上，基于数学分析，在Matlab/Simulink环境中，建立了一种新的a-b轴系下考虑铁耗的三相异步电机模型。本文的第2节将详细介绍此电机模型，并给出实际的仿真模型结构，同时将此模型空载工况下的计算机仿真结果与真实电机空载实验结果作对比，说明其正确性。

到目前为止，在众多的功率理论中，有代表性并且应用很广泛的两种理论分别是瞬时无功功率(Instantaneous Reactive Power，IRP)理论[10]和标准IEEE Std 1459-2010中所提的功率分析理论[11]。日本学者Akagi等人在1984年提出的IRP理论是一种基于时域变换的功率理论，此功率理论从一个新的角度解释了无功功率的物理意义，可以用于分析稳态和暂态下三相电气系统的功率特性。因此，该理论一经提出便在国际上引起了强烈的反响。然而，标准IEEE Std 1459-2010中所提功率分析理论在总结前人的研究成果的基础上，将单相电路和三相电路在不同工况下的功率评估理论做了统一的规范。本文第3节将详细介绍这两种理论。

IRP理论和标准IEEE Std 1459-2010中所提功率理论各具特色，都有其适用的场合。但是在PWM驱动电机能效测试领域，鲜见其应用特性的比较。因此，在本文第4节，将首先利用第2节所建立的电机损耗模型搭建一个典型的PWM驱动电机系统算例，然后分别利用IRP理论和标准IEEE Std 1459-2010中所提理论，对电机的损耗进行评估。最后，在第5节结论中，比较两种理论下电机损耗的评估结果，总结出两种功率理论在PWM驱动电机能效测试领域中的应用特点。

2 考虑铁耗的电机损耗模型

目前，由于没有统一的标准提供评估真实电机的方法，且真实电机在非正弦电压电流作用下的内部变量获得具有一定的难度，文献[8]指出，附加损耗所占电机损耗的比例很低，因此本文忽略了附加损耗，建立了考虑损耗的电机损耗模型，并在正弦条件下，将其外特性和效率与实验室真实电机的空载特性和根据标准实测出的额定负载工况下效率作对比，旨在验证使用此模型的内部变量计算得到的电机损耗在一定程度上是真实可信的。

2.1 等效数学模型

在对电机进行数学分析之前，先作如下假设：①定、转子三相绕组完全对称；②定、转子表面光滑无齿槽效应，且气隙磁动势在空间呈正弦分布；③定转子绕组的匝数相等。考虑到异步电动机的铁心损耗，根据电机学[12]知识，在a-b静止坐标系下的异步电动机的数学模型表示如下。

定、转子电压方程为：

(1)

励磁电流方程为：

(2)

磁链方程为：

(3)

电磁转矩方程为：

(4)

电机运动方程为：

(5)

根据式(1)～式(5)，可以得到异步电动机的等效电路，如图1所示。

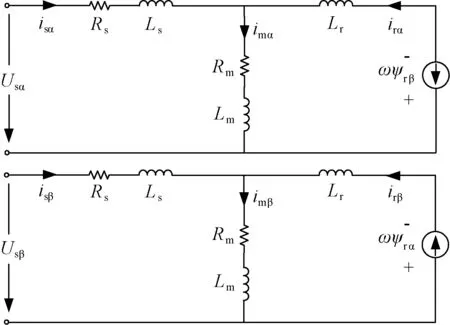
图1 α-β静止坐标系下，考虑铁耗的三相异步电动机等效电路图Fig.1 Motor equivalent circuit with iron loss in α-β static frame

在上述模型中，Rs、Rr和Rm分别表示定、转子以及铁损的等效电阻；Ls、Lr和Lm分别表示定、转子漏感及互感；Usa、Usb分别表示α，β轴定子电压；isα、isβ、irα、irβ分别表示α、β轴定、转子电流；imα、imβ分别表示α、β轴励磁电流；ψsα、ψsβ、ψrα、ψrβ分别表示α、β轴定、转子磁链；ψmα、ψmβ分别表示α、β轴主磁链；Te、TL分别表示电磁转矩和负载转矩；np、J分别表示电机极对数和电机转动惯量；ω、p分别表示电角速度和微分算子。

2.2 Matlab仿真模型

本仿真模型选择定子电压Usα和Usβ、负载转矩TL作为输入变量，定子电流isα和isβ、电磁转矩Te和转子电角速度ω作为输出变量，其他作为中间变量。根据式(1)～式(5)在Matlab/Simulink环境中搭建考虑铁耗的三相异步电动机仿真模型，如图2所示。

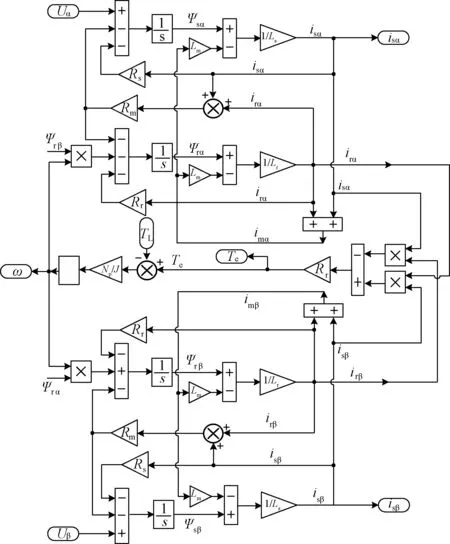
图2 α-β静止坐标系下，考虑铁损的三相异步电机仿真模型图Fig.2 Motor simulation model with iron loss in α-β static frame

2.3 仿真与实测结果对比

为证明仿真模型的正确性，本文选用实验室用JZR211-6型电机(额定功率2.2kW，额定电压380V，额定转矩23.3N·m，50Hz，3对极，其他参数如表1所示)进行仿真和实验验证，同时选取额定电压380V、频率50Hz电源驱动电机。在此条件下，按照电机空载试验的步骤，在不同电压下，对此电机做空载实验。同时利用此参数，在相同供电情况下，对仿真模型进行仿真实验。图3为根据实验数据和仿真数据绘制的输入功率(Pin)与定子电压(Us)曲线图。从图中可以看出，在给定相同的定子电压时，本文所建立的考虑铁耗的电机仿真模型的输入功率与实际电机输入功率的平均误差小于5%。在电机空载时，由于附加损耗可以忽略不计，其输入功率即为电机的实际损耗。因此，由图3可知，使用此损耗模型计算得到的电机损耗与电机的真实损耗相差较小，可以将此损耗模型内部变量计算的损耗认为是电机真实损耗。

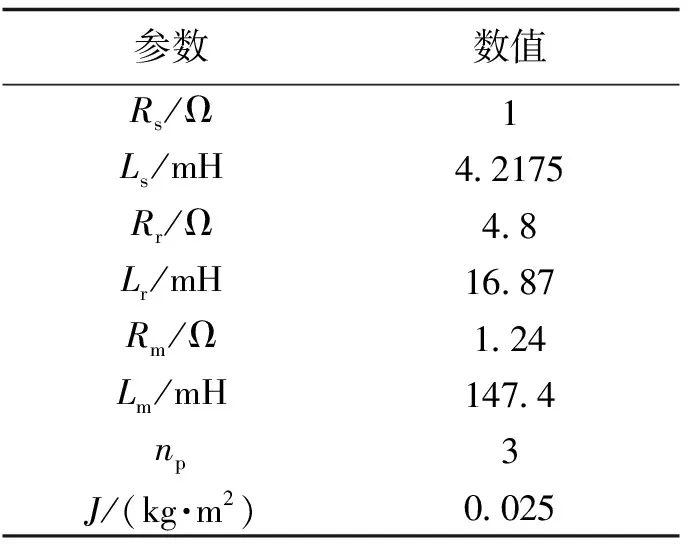
表1 考虑铁耗的异步电机仿真参数

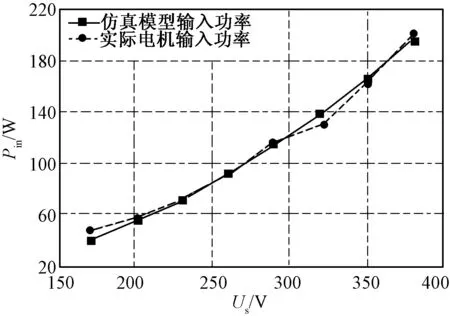
图3 输入功率-定子电压关系曲线Fig.3 Pin(input power) versus Us(stator voltage) curves of motor and simulation model

3 IRP理论和标准IEEE Std 1459-2010

3.1 IRP理论

设三相电路各相电压和电流的瞬时值分别为va(t)、vb(t)、vc(t)和ia(t)、ib(t)、ic(t)，如图4所示。

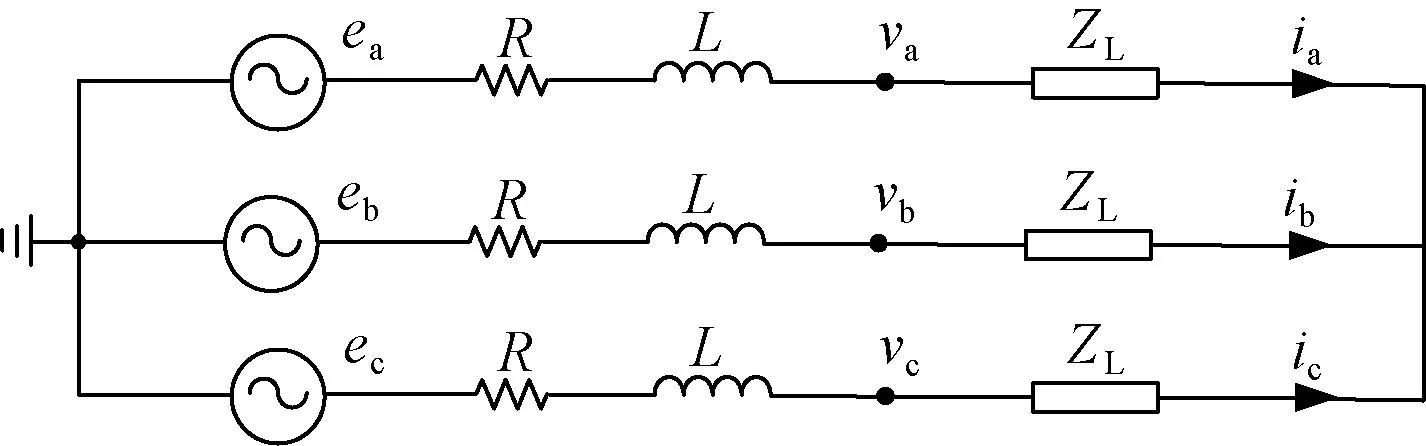
图4 三相电路示意图Fig.4 Three-phase circuit

日本著名学者在文献[10,13]中，将瞬时实功功率p和虚功功率q定义如下，其中，电压和电流都通过Clark变换到了α-β坐标系下，并分解得到α，β轴上的有功电流iαp、iβp和无功电流iαq、iβq。

(6)

即有：

(7)

因此，可得α、β轴上的电流分量为：

(8)

此时，α、β轴上瞬时有功功率和无功功率分别定义为：

(9)

(10)

式中

(11)

此理论中，将瞬时视在功率定义为：

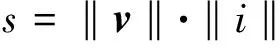
(12)

式中，v=(vα,vβ)；i=(iα,iβ)。本文在原有IRP理论的基础上对瞬时视在功率的表达式进行更深入的推导可得：

(13)

式中，q为IRP理论中定义的瞬时虚功率。因此可知，IRP理论中的视在功率的本质是由实功率和虚功率合成的。实功率中包含有功功率和无功功率，虚功率中包含的是α、β轴间的交换功率。

3.2 标准IEEE Std 1459-2010

在周期的非正弦三相电路中，IEEE Std 1459-2010标准[10]对各种功率的计算进行了描述。首先，规定了需测量的电气量有线电压vab、vbc、vac和相电流ia、ib、ic，并据此定义了三相瞬时有功功率p：

(14)

然后在固定周期T(一般取市电工频50Hz)下，求得有功功率P：

(15)

定义视在功率为：

Se=3VeIe

(16)

该标准将等效相电流Ie分解为等效基波电流Ie1和等效总谐波电流IeH，在三相系统中，其表达式分别为：

(17)

(18)

(19)

式中，Ia、Ib和Ic为三相总电流有效值;Ia1、Ib1和Ic1为三相基波电流有效值;IaH、IbH和IcH为三相总谐波电流有效值。

同理，等效电压分量Ve也可以分解基波电压Ve1和总谐波电压VeH，其表达式分别为：

(20)

(21)

(22)

式中，Vab、Vbc和Vca为总线电压有效值;Vab1、Vbc1和Vca1为三相基波电压有效值;VabH、VbcH和VcaH为三相总谐波电压有效值。

因此，总视在功率可以分解为基波视在功率Se1和非基波视在功率SeN，其中

(23)

而非基波视在功率又可以细分为电压畸变功率DeI，电流畸变功率DeV和谐波视在功率SeH，其数学关系式为：

(24)

式中

(25)

4 算例分析

4.1 算例搭建

为了验证第3节所述两种理论在PWM驱动电机能效测试中的适用情况，本文在Matlab/Simulink环境中搭建了一个仿真算例，示意图如图5所示。

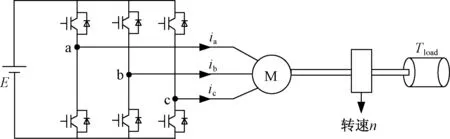
图5 PWM驱动电机能效测试仿真算例示意图Fig.5 Simulation example of PWM-fed motor efficiency estimation

图5中，逆变器直流侧电压E为800V，采用SPWM调试方法，开关频率为1500Hz，调制比为0.7757，驱动带有恒转矩负载为Tload(N·m)的异步电动机，并测量电机的转速，其中，异步电动机的仿真模型采用第2节中所提出的考虑铁耗的三相异步电动机损耗模型。

4.2 结果与分析

根据4.1节仿真算例，分别在不同负载(0～TN)工况下测量稳态时三相异步电机的输入电压、输入电流、转子电流、励磁电流和转速，然后分别采用IRP理论和标准IEEE Std 1459-2010中的功率理论评估此电机的能效，并将其与通过电机内部变量计算的实际电机损耗比较，得到的电机输出功率曲线和电机效率对比结果图，分别如图6和图7所示。

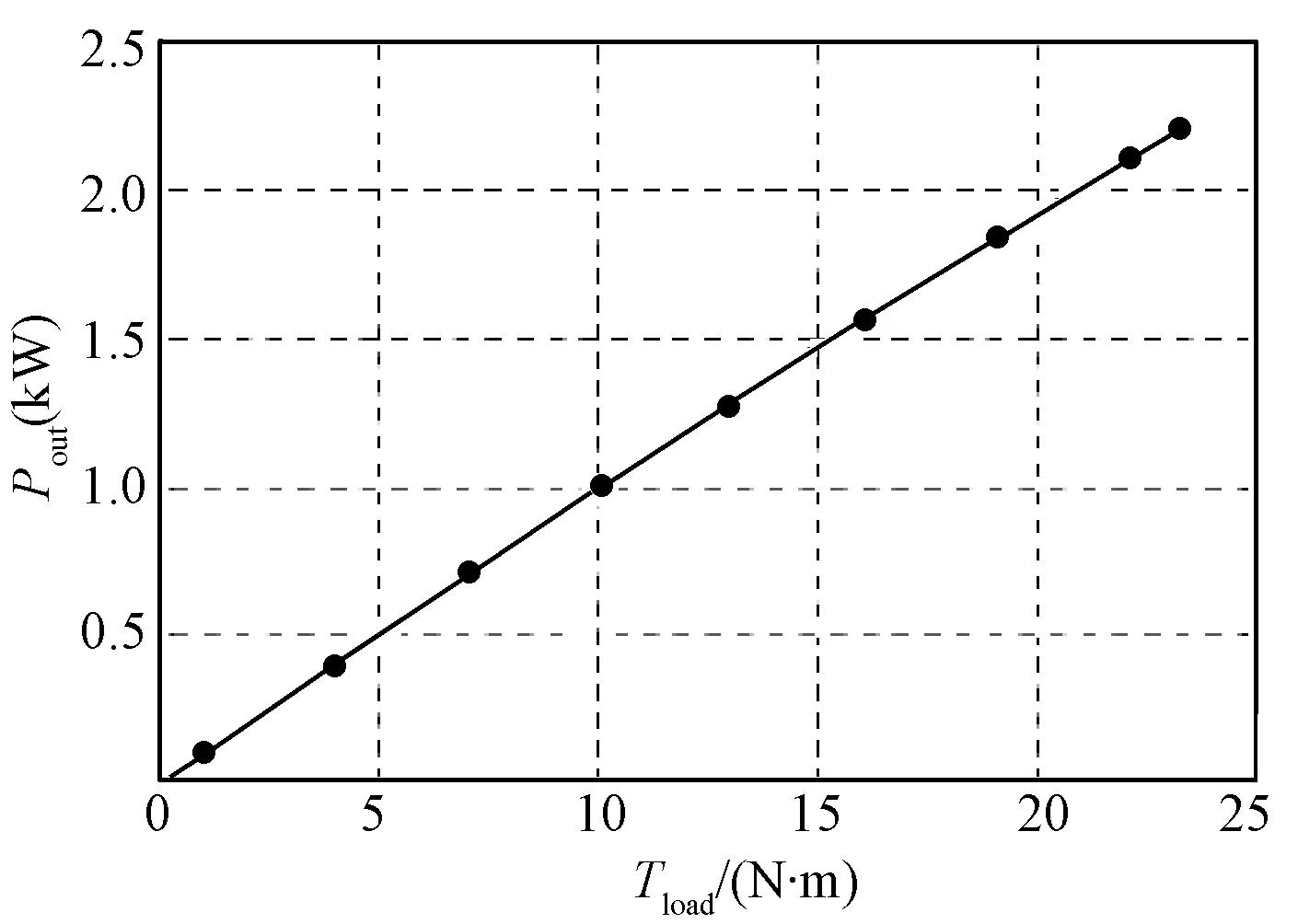
图6 不同负载工况下，电机输出功率曲线Fig.6 Output power curve of motor with different loads

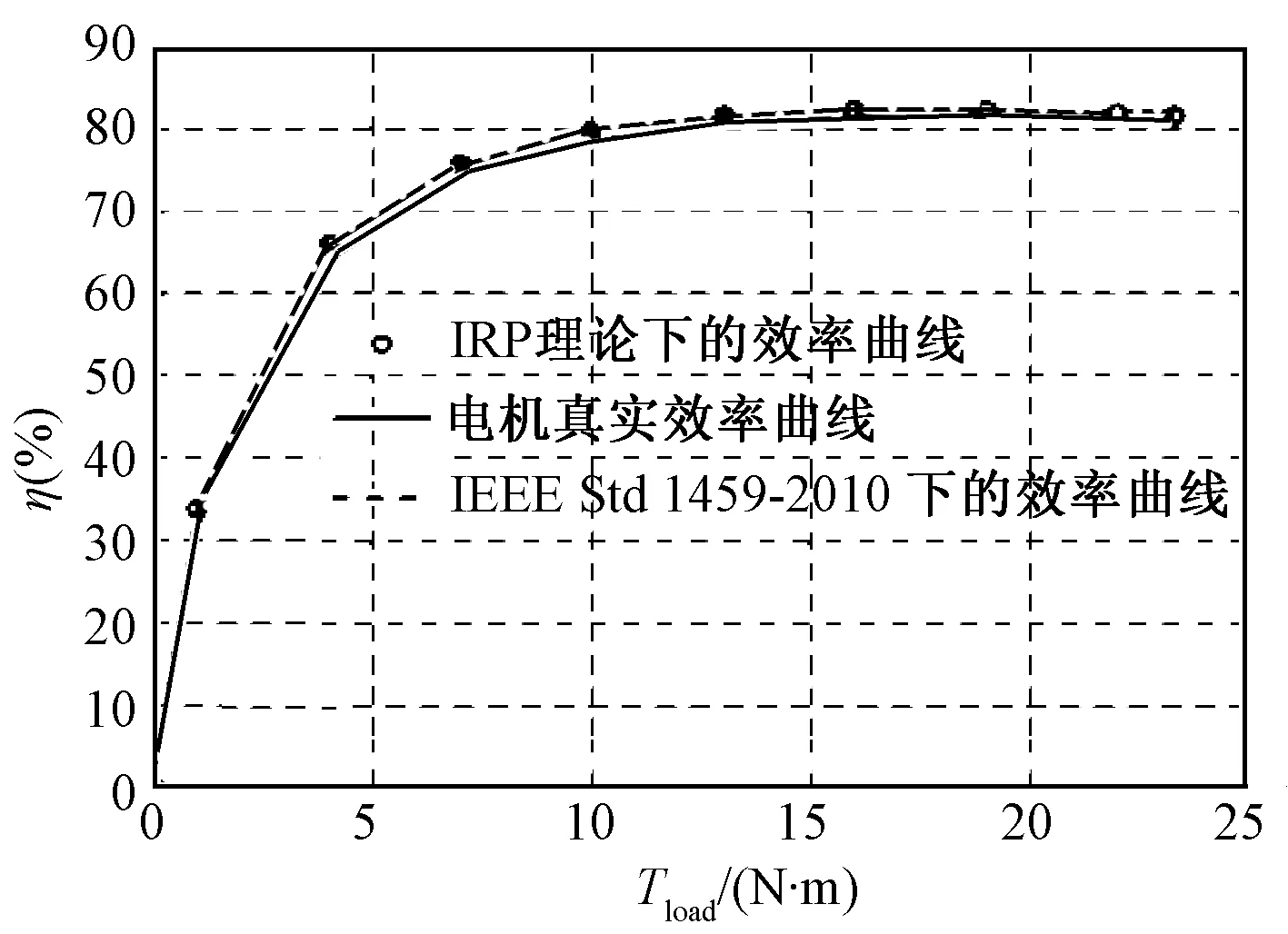
图7 不同负载工况下，两种功率理论对电机效率评估效果的对比图Fig.7 Contrast of motor efficiency estimations between IRP theory and IEEE Std 1459-2010 method with different loads

由图6的仿真分析可知，在额定基波电压下，PWM驱动电机的输出功率随着负载转矩在0～TN的变化而逐渐增大。图7为在额定基波电压、不同负载转矩的工况下，将IRP理论和IEEE Std 1459-2010标准对电机效率所作的评估，与由电机内部实际损耗计算得到的电机真实效率分别作对比。由第3节中对IRP理论和标准IEEE Std 1459-2010的介绍可知，两种理论对瞬时有功功率的定义是等价的，因此在电机进入稳态后，输入电机的有功功率在两种功率理论下的计算结果应该是完全一致的，这与图7中实际算例的效率评估结果相符。对比图7中的电机真实效率曲线和两种理论的效率评估曲线可知，在额定负载下，这两种功率理论可以很精确地评估电机的效率，但是在电机轻载时，这两种功率理论对电机吸收的有功功率的评估略偏小。

当PWM驱动电机所带恒转矩负载在0～TN变化时，分别使用IRP理论和标准IEEE Std 1459-2010评估输入电机的视在功率，结果如图8所示。由此算例分析可知，标准IEEE Std 1459-2010的电机视在功率始终比IRP理论大。这主要是由于两种理论对视在功率的定义不同。IRP理论通过式(12)定义了视在功率，但是根据式(13)的分析可知，此视在功率中不包含IRP理论定义的无功功率，因此IRP理论中定义的视在功率不能真实地反映系统的容量。而标准IEEE Std 1459-2010视在功率包括了非正弦非周期电路中所有种类的功率现象，比IRP理论能更全面地反映系统的容量。

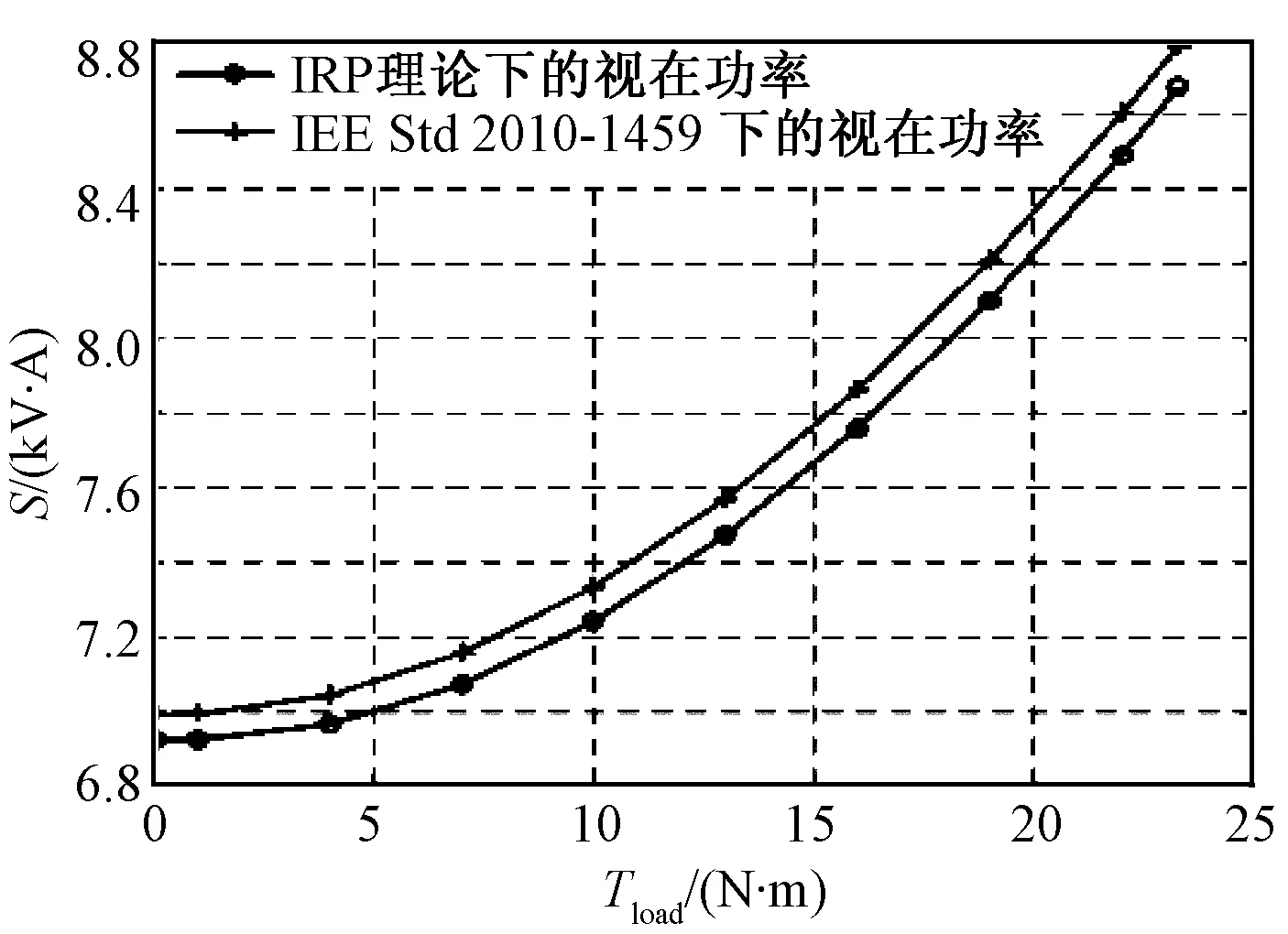
图8 不同负载工况下，两种功率理论对电机输入视在功率评估效果的对比图Fig.8 Contrast of motor apparent power between IRP theory and IEEE Std 1459-2010 method with different loads

5 结论

本文首先通过对电机的数学分析，在a-b静止坐标系下推导了考虑铁耗的电机数学模型，并在Matlab/Simulink环境中搭建了三相异步电动机的仿真模型，经过与实验室真实电机对比，验证了仿真模型的正确性和使用模型内部变量计算电机损耗的有效性。本文利用此考虑铁耗的电机仿真模型构建了一个PWM驱动电机能效测试仿真算例，分别利用IRP功率理论和IEEE Std 1459-2010标准中提供的功率计算方法，对算例中的电机进行能效评估。通过将其与利用电机模型内部电压、电流和模型参数计算得到的电机能效相比，可以发现：①两种功率理论对有功功率的评价是等效的，在额定负载下，两种功率理论对有功功率的评价与电机真实吸收的有功功率基本一致，但是在电机轻载时，这两种功率理论对电机吸收的有功功率的评价略偏小；②经过理论和仿真分析可知，在变流器驱动电机视在功率的评估方面，相比于IRP理论定义的视在功率，IEEE Std 1459-2010标准对非正弦三相平衡系统中的视在功率的分析全面、精细，更适用于评估变流器驱动电机视在功率。但是标准IEEE Std 1459-2010也有一大缺点，即没有对无功功率做出更加详细的描述，并且其物理意义不明确，这一问题亟待进一步解决。

[1] 肖湘宁，罗超，陶顺 (Xiao Xiangning, Luo Chao, Tao Shun). 电气系统功率理论的发展与面临的挑战 (Development and challenges of power theory in electrical power system) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2013, 28(9): 1-10.

[2] 刘陵顺，田锦昌 (Liu Lingshun, Tian Jinchang). 考虑铁损时异步电动机的最佳效率控制 (Optimal-efficiency control of asynchronous motor taking core loss into account) [J]. 微电机(Micromotors), 2001, 34(4): 50-53.

[3] 赵海森 (Zhao Haisen). 超高效异步电机损耗模型及降耗措施研究 (Study on loss model and loss reducing measures of premium asynchronous motors) [D]. 北京: 华北电力大学 (Beijing: North China Electric Power University), 2011.

[4] Sousa G C D, Bose B K, Cleland J, et al. Loss modeling of converter induction machine system for variable speed drive [A]. Proceedings of the 1992 International Conference on Industrial Electronics, Control, Instrumentation, and Automation [C]. 1992. 114-120.

[5] 陈其工 (Chen Qigong). 变频调速异步电机模型研究 (Research on the model of variable frequency motor) [J]. 微特电机 (Small & Special Electrical Machines), 1996,24 (2): 2-4.

[6] 陈其工 (Chen Qigong). 变频运行感应电动机谐波电流计算与转矩、损耗分析 (The computation on harmonic current and analysis on ripple torque and loss of induction motor equipped with the converter) [J]. 微特电机 (Small & Special Electrical Machines), 1999, 27(3): 33-35.

[7] Nicol Hildebrand E, Roehrdanz H. Losses in three-phase induction machines fed by PWM converter [J]. IEEE Transactions on Energy Conversion, 2001, 16(3): 228-233.

[8] 张立伟，温旭辉，陈桂兰 (Zhang Liwei, Wen Xuhui, Chen Guilan). Matlab/Simulink 环境下异步电机建模及其工程应用 (The modeling of induction motor in Matlab/Simulink and its techno-application) [J]. 电气应用 (Electrotechnical Application), 2006, 25(4): 119-122.

[9] 宋鹏先，李耀华，王平, 等 (Song Pengxian, Li Yaohua, Wang Ping, et al.). 三相电力电子负载谐波分析与抑制(Harmonic analysis and inhibition of three-phase power electronic loads) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(2): 25-33.

[10] Akagi H, Kanazawa Y, Nabae A. Instantaneous reactive power compensators comprising switching devices without energy storage components [J]. IEEE Transactions on Industry Applications, 1984，IA-20 (3): 625-630.

[11] IEEE Std 1459-2010, IEEE standard definitions for the measurement of electric power quantities under sinusoidal, non-sinusoidal, balanced, or unbalanced conditions [S].

[12] 辜承林，陈乔夫，熊永前 (Gu ChengLin, Chen Qiaofu, Xiong Yongqian). 电机学 (Electric machinery) [M]. 武汉：华中科技大学出版社(Wuhan：Huazhong University of Science & Technology Press), 2001.

[13] Akagi H, Watanabe E H, Aredes M. Instantaneous power theory and applications to power conditioning [M]. John Wiley & Sons, 2007.

(，cont.onp.12)(，cont.fromp.6)

Comparisons on application of IRP theory and IEEE Std 1459-2010 for converter fed motor system efficiency evaluation

YANG Li-min1,2, LI Yao-hua1, WANG Ping1, LI Zi-xin1, CUI Dong-dong1,2

(1. Key Laboratory of Power Electronics and Electric Drive, Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)

Converters have been widely used in motor driving systems. However, the traditional power theory does not work well at evaluating motor efficiency under the non-sinusoidal situations. So the IRP theory and IEEE Std 1459-2010, which are popular in the field of describe the power phenomenon under the non-sinusoidal situations, are introduced. In this paper, a new motor simulation model with iron losses has been proposed based on mathematical analysis on motors. Then a typical PWM fed motor system has been built on the base of the proposed motor simulation model with iron losses above. The system is used as an example, with which the power phenomenon has been researched by the methods in IRP theory and IEEE Std 1459-2010. The results show that the motor efficiency can be evaluated accurately by using both IRP theory and IEEE Std 1459-2010. However, IEEE Std 1459-2010 is more suitable for evaluating apparent power then IRP theory, and IRP theory works more better then IEEE Std 1459-2010 in reactive power evaluation.

motor efficiency; motor loss simulation model; instantaneous reactive power theory; IEEE Std 1459-2010

2015-06-08

中国科学院重点部署课题资助项目(KGZD-EW-302-2)

杨立敏(1991-)， 男， 山西籍， 博士研究生， 研究方向为高压大功率电力电子变流器； 李耀华(1966-)， 男， 河南籍， 研究员， 博士生导师， 研究方向为电力电子与电机驱动。

TM46

A

1003-3076(2016)01-0001-06