采用阶跃函数分析经历地震的大坝安全监测数据

陈　容，冉　蠡，杨　杰，程　琳

(1.大唐碧口水力发电厂，甘肃省文县　746412；2.西北旱区生态水利工程国家重点实验室培育基地，西安　710048)



采用阶跃函数分析经历地震的大坝安全监测数据

陈容1，冉蠡2，杨杰2，程琳2

(1.大唐碧口水力发电厂，甘肃省文县746412；2.西北旱区生态水利工程国家重点实验室培育基地，西安710048)

摘要：大坝经历大地震后，坝体位移监测数据会发生明显突变。利用传统统计模型对监测数据进行建模，拟合程度较低、效果较差。为此，将阶跃函数引入传统统计模型中，重新构建回归分析模型。以碧口大坝竖向位移监测数据资料为例，分别采用传统统计模型和阶跃函数模型进行逐步回归分析，并利用阶跃函数监测模型分离地震分量，通过分析地震对大坝竖向位移的影响规律，以验证阶跃函数模型的优越性。分析结果表明，阶跃函数模型的拟合精度及预测效果均高于传统模型，可供类似工程参考。

关键词：大坝监测；阶跃函数；地震突变；逐步回归分析；地震分量；统计模型

0前言

大坝安全监测是对水利工程相关结构、设施及周围环境通过仪器监测或人工巡视所做的测量及观察。而所得到的相关数据及其变化是对大坝运行情况的真实反映。因此，真实、准确地分析监测数据对于确定大坝运行状态与大坝安全鉴定有着重要意义。大坝监测数据在遭受地震等自然灾害后，由于地震荷载作用或仪器损坏而出现突变点，给建立大坝安全监测模型与数据回归分析增加了难度，使得传统统计模型对大坝监测数据的回归分析结果与实测值的拟合效果较差，进而不能较好地体现出各影响因子对效应量的影响程度。此情况表明，传统统计模型不适用于经历地震的大坝监测数据，需要重新建立新模型。鉴此，本文基于传统统计模型，运用单位阶跃函数构建出大坝安全监测数据回归分析的阶跃函数监测模型，并将该模型运用于碧口大坝监测数据的回归分析中。通过与常规模型相比，证明阶跃函数监测模型具有精度高、拟合效果好、能较好地反映各影响因子与效应量间的关系等优点。

1单位阶跃函数

单位阶跃函数具有许多特性，若一般函数能用它表示出来，那么对研究问题或运算将十分有益。

阶跃函数定义为：

(1)

式中：uA为阶跃函数；t、t0分别为变量；A为常数。

函数图像如图1所示。

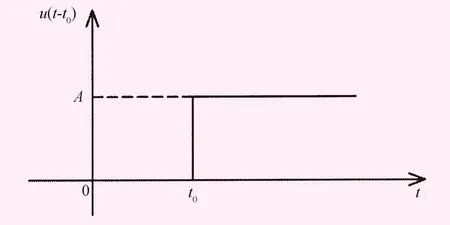
图1　阶跃函数图像图

当常数A=1时，式(1)为单位阶跃函数，记作：

(2)

利用阶跃函数，将分段函数用1个函数来表示[1-2]。如分段函数：

(3)

式中：f1(t)和f2(t)分别为[0，t0]和[t0，+∞]上的连续函数，则有：

(4)

2土石坝位移监测模型

2.1传统统计模型

影响大坝坝体竖向位移的主要因素有库水压力、温度变化和时效等，因此，竖向位移由水压分量δH、温度分量δT和时效分量δθ组成，即：

(5)

作用在坝体的静水压力，与坝体在水压荷载下的因渗流影响产生竖向位移，是水压荷载对大坝竖向位移作用的2个主要方面。由于渗流的产生时间相对于库水位的变化时间具有滞后性，所以水压因子的取值为测点在监测日前1～3 d、4～10 d、11～30 d、31～60 d所对应的上游库水位的平均值。水压分量δH表示为：

(6)

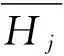
因为气温为周期性变化，因此温度分量用正弦函数与余弦函数的周期项来表示。温度分量δT为：

(7)

式中：t为监测日至监测基准日的累计天数；t0为第1个测值日至监测基准日的累计天数；b1i、b2i分别为温度因子回归系数。

选择时效分量δθ表达式为：

(8)

式中：θ为监测日至监测基准日的累计天数除以100；θ0为第1个测值日至监测基准日的累计天数除以100；c1、c2分别为时效因子回归系数[3]。

通过上述分析得出，大坝竖向位移的统计模型如下：

δ=δH+δT+δθ+a0

c1(θ-θ0)+c2ln(θ-θ0)+a0

(9)

式中：a0为常数项。

2.2基于阶跃函数的大坝竖向位移监测模型表达式

为提高监测模型精度与拟合效果，使之能较好地模拟监测资料的突变和波动变化，并能正确地反映出各影响因子与效应量间的关系，故在传统统计模型基础之上引入单位阶跃函数，以进行拟合修正[4-7]。单位阶跃函数主要用于修正传统统计模型中的时效分量，修正后的竖向位移监测模型为：

δ=δH+δT+δθ+a0

(10)

2.3突变点判定

在实际监测数据中，地震与观测误差均能使监测数据产生突变。地震引起的突变是由于地震荷载作用或仪器损坏而致，虽突变后监测值较突变前监测值呈整体增大或减小，但测值变化仍可正确反映所监测项目的真实性态；观测误差是由于观测者主观疏忽或外界客观因素影响，使个别监测数据较其前后测值呈突然增大或减小。存在观测误差的监测值属于错误的监测数据，其不能正确地反映出监测项目的真实性态，应对其进行剔除。一般用来剔除监测数据系列中观测误差的方法有：格罗布斯准则、狄克松准则、肖维勒准则、罗曼诺夫斯基准则、3σ准则等，其中3σ准则是最简单、最常用的处理观测误差的方法[8-9]。

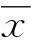
3实例

3.1工程及监测概况

位于甘肃省文县碧口镇的碧口水电站是白龙江干流上最早开发的梯级电站。此工程布置了较为全面的监测措施，其中，土石坝的竖向位移监测为主要监测项目之一。在施工期，用于监测竖向位移的15支沉陷监测管，分别布置在坝身的3个断面、深墙顶、宽墙等部位。但到1974年底，这些监测管全部损坏。大坝竣工后，分别在原坝体上下游7个纵断面上又增设多个横断面监测点，共布设了47个测点以监测大坝竖向位移。从施工结束后至1977年9月开始起测时，有47个大坝竖向位移测点可以监测，随着设备失效老化、地质活动等原因，其中部分测点仪器已经损坏，但经过不断修缮，到目前仍在进行监测的测点有42个[12-13]。测点标号及位置见图3。对这42个测点的监测数据资料，分别建立传统统计模型和阶跃函数模型进行逐步回归分析，并对模型计算结果进行对比分析。

图2　回归计算流程图

3.2回归计算分析

现以大坝坝体D9-1测点的竖向位移监测资料为例，观测资料时间序列为1995年1月7日至2014年12月9日，此期间监测资料因2008年5·12地震和地震后监测仪器的修复和升级改造而出现突变点。建立传统模型、分段模型和阶跃函数模型，利用matlab软件分别进行逐步回归分析，以检验阶跃函数模型的分析效果。其中，分段模型是利用传统模型在数据突变处两侧分别建模。阶跃函数模型中分别设置2008年5月13日和2009年1月8日为数据突变点。

利用式(9)、(10)对测点D9-1的竖向位移监测数据进行回归计算。复相关系数R、剩余标准差S与显著水平F见表1，图4所示是对测点进行3种回归模型计算的实测值与拟合值过程线。

表1　2种模型回归分析参数对比表

由表1可看出，阶跃函数监测模型的复相关系数(0.993)大于传统统计模型的复相关系数(0.885)，传统统计模型剩余标准差(41.2)大于阶跃函数监测模型剩余标准差(10.3)。采用传统模型进行分段建模的复相关系数分别为0.999、0.628，两者复相关系数相差较大、拟合效果不稳定，同时剩余标准差分别为11.7、17.2，两者均大于阶跃函数监测模型。当数据资料突变点较多时，进行分段建模分析的工作量会大大增加，效率降低。由此可知，阶跃函数监测模型的精度和运行效率高于传统模型。

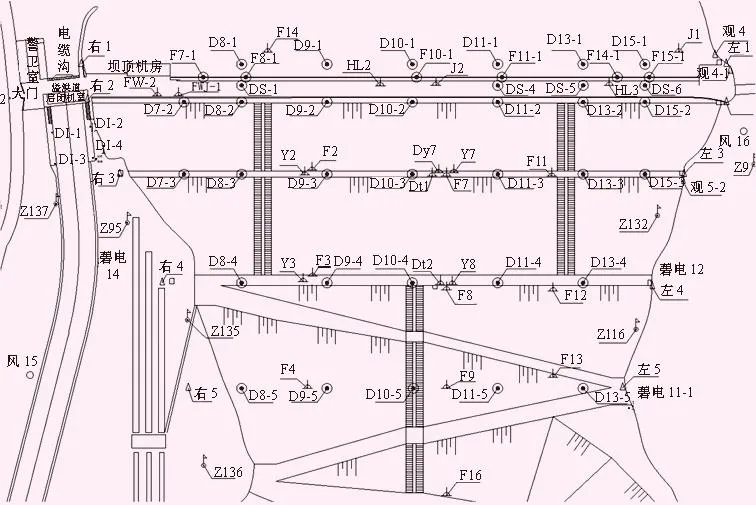
图3　碧口大坝监测布置图

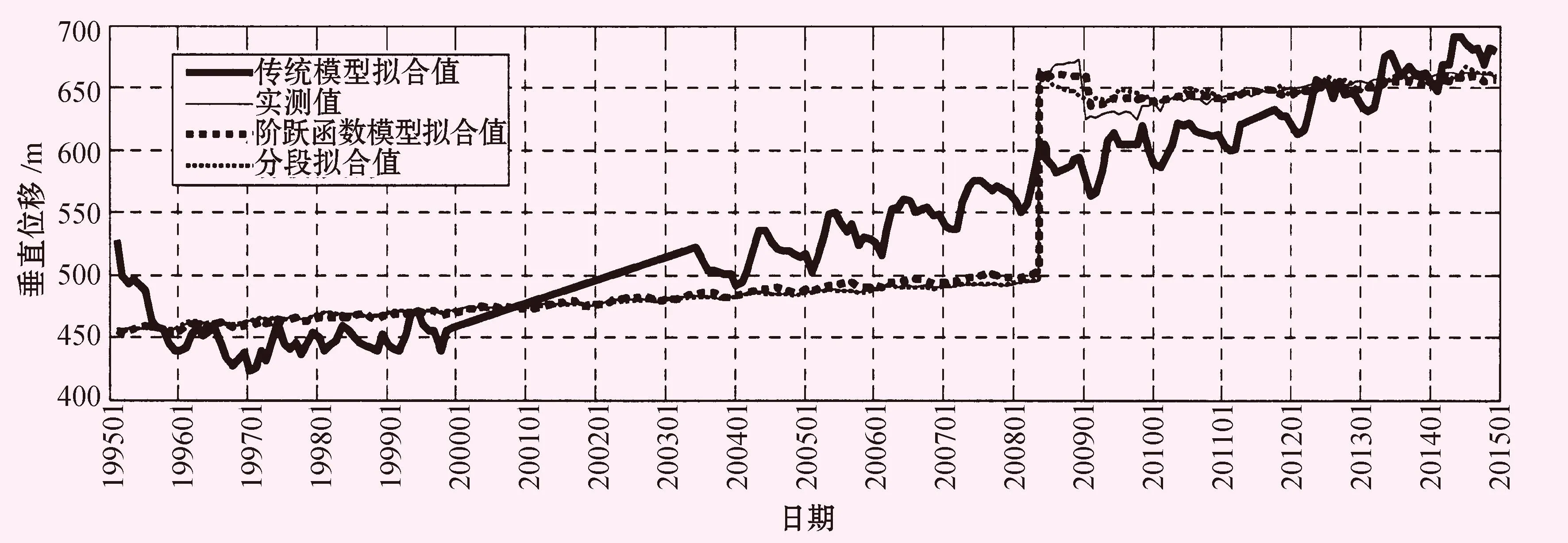
图4　3种模型回归分析后的拟合值与实测值过程线图

由图4可看出，在2008年5月13日和2009年1月8日这两处监测数据发生突变的时间点前后，阶跃函数监测模型的拟合值比传统模型的拟合值更接近实测值。与分段建模相比较，阶跃模型与分段1的拟合程度相似；在分段2处，阶跃模型的拟合值更接近实测值。由此可见，阶跃函数监测模型的拟合效果好于传统模型和分段建模，拟合值更为接近实测值。

3.3地震效应分离与大坝竖向位移变化速率分析

大坝在经历地震后，地震分量在时效分量中占有绝大比重。从时效分量中分离出地震分量，通过分析地震分量大小可得出地震效应对大坝各部分的影响情况。现对大坝下游0+041.80 m(下游纵断面)，坝左0+224.00 m(最大横剖面)，0+304.00 m(岸坡横断面)3个断面的测点拟合值分离地震分量，分离出的地震分量见图5～7，大坝位移变化速率见表2。

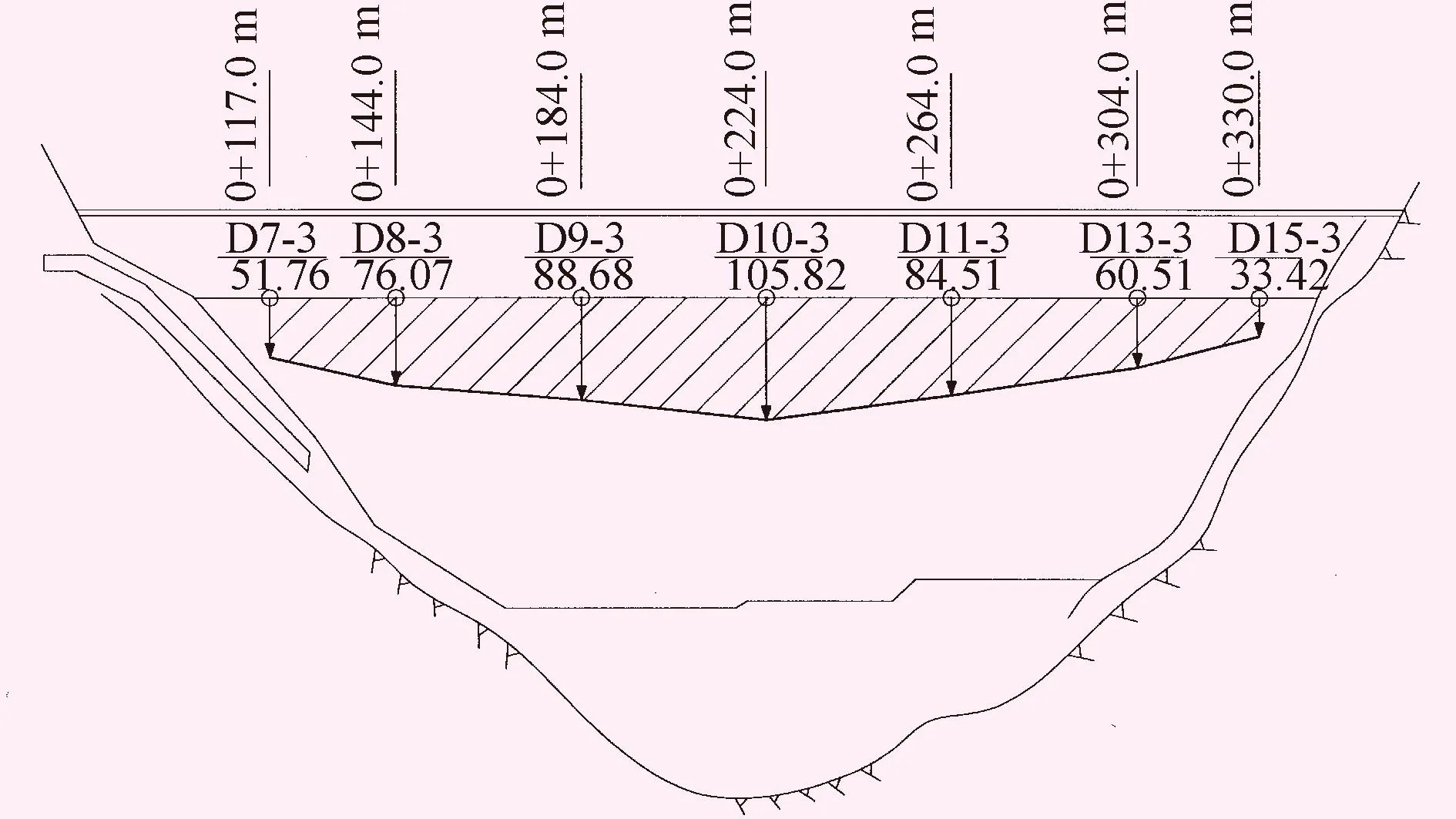
图5下游纵断面(0+041.80 m)各测点地震分量　单位：mm

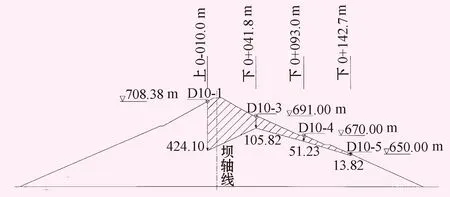
图6最大横断面(0+224.00 m)各测点地震分量　单位：mm

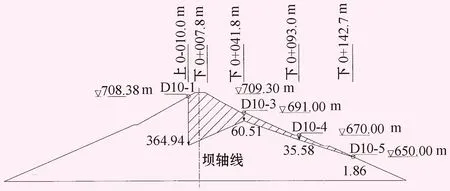
图7岸坡横断面(0+304.00 m)各测点地震分量　单位：mm

由图5可看出，各测点的地震分量并不相同，表明地震对大坝各部分的影响不同。在图5所示断面中，在大坝中部D10-3测点处的地震分量最大，向两岸坝肩方向的测点地震分量依次减小。表明地震对大坝中部河床坝段的影响大于岸坡坝段，越靠近两岸的坝体，地震对其影响越小。在图6、7所示横断面中，大坝中部靠近坝顶处的测点的地震分量大于下游坝段，越往下游地震分量越小。表明地震对大坝坝顶处的影响大于下游坝坡，且越靠近下游的坝体，地震对其影响越小。此分析结果符合以往土石坝地震模拟试验的相关结论[14-16]。

表2　大坝竖向位移变化速率表　mm/a

由表2可看出，地震时因地震荷载作用，坝体部分土体液化或松动而不稳定。在地震后的几年中，大坝土体在自重和水压力等作用下重新稳定，即地震后大坝竖向位移变化速率较地震前明显加快，之后速率逐年递减，随时间推移而趋于平稳。

3.4结果分析

由上述分析可知，相较于传统统计模型，阶跃函数监测模型的精度高、拟合效果好。且通过模型分离的地震分量，分析得出地震(影响因子)对于大坝各部分竖向位移的影响程度(效应量)关系相同于以往的相关实验结论，即符合土石坝坝体竖向变形的一般规律。表明在分析经历地震的大坝监测数据中，阶跃函数监测模型较传统模型具有先进性、客观合理性。可用该模型对因地震等自然灾害或其他原因而产生突变的监测资料分离各分量，进而进行定量分析。

4结语

以碧口大坝监测资料为例，在传统统计模型中引入单位阶跃函数，修正为阶跃函数监测模型。同时建立传统统计模型和阶跃函数监测模型，利用matlab软件分别进行逐步回归分析，比较两者模型精度与拟合效果，并运用阶跃函数监测模型分离出地震分量，以分析地震对大坝竖向位移影响性态。分析结果表明，阶跃函数监测模型回归分析效果远优于传统统计模型，回归计算参数更为合理、拟合效果好，计算分析成果符合相关实验规律，可供类似监测项目参考使用。

参考文献:

[1]李祖斌,黄淑贞.一般函数的单位阶跃函数表达式[J].集美航海学院学报,1994,12(1):71-74.

[2]田社平,陈洪亮,李萍.阶跃函数的定义及其在零点的取值[J].电气电子教学学报,2005,27(2):38-40.

[3]陈德平,韩云峰,雷剑,等.碧口土石坝竖向位移监测的逐步回归模型拟合与分析[J].西北水力发电,2006(22):142-145.

[4]杨金凯,包腾飞,朱凯,等.棉花滩碾压混凝土重力坝裂缝计阶跃函数监控模型[J].水电能源科学,2013,31(10):67-69.

[5]徐波,程琳,荆凯.岩滩大坝钢板计阶跃函数监控模型[J].水电能源科学，2010,28(2):75-77.

[6]陈龙.溢流坝段水平位移混合模型的建立[J].大坝与安全，2003(01):60-62.

[7]李铮,李宏恩,袁启旺,等.阶跃函数模型在龙江水电站压力钢管监测中的应用[J].水电能源科学，2011,29(7):97-100.

[8]熊艳艳,吴先球.粗大误差四种判别准则的比较和应用[J].大学物理实验，2010,23(1):66-68.

[9]梁晓红. 轧辊测量数据粗差剔除的3σ应用研究[J].科技信息，2006(12):66-68.

[10]许贝贝,崔晨风.大坝自动化监测数据粗差处理方法研究[J].测绘地理信息，2015,40(2):59-61.

[11]覃欣,熊娟.LabVIEW数据处理中3σ准则的应用[J].中国测试，2009,35(5):66-69.

[12]陈容,刘林.震后碧口大坝安全监测资料分析[J].大坝与安全，2011(03):43-46.

[13]朱晟,石高峰,周建平.碧口心墙堆石坝抗震复核分析[J].岩石力学与工程学报，2011，30(增1):2954-2962.

[14]陈宁,杨正权,袁林娟,等.两河口水电站高土石坝地震反应地震模拟振动台模型试验研究[J].水利水电技术,2010,41(10):80-86.

[15]杨正权,刘小生,汪小刚,等.高土石坝地震动力反应特性大型振动台模型试验研究[J].水力学报,2014,45(11):1361-1372.

[16]刘福海. 土石坝地震破坏机理振动台试验研究[D].大连：大连理工大学，2012.

Analysis on Safety Monitoring Data of Dam Experiencing Earthquake by Step Function

CHEN Rong1, RAN Li2, YANG Jie2, CHENG Lin2

(1. Datang Bikou Hydropower Plant, Wenxian, Gansu746412, China;2. State Key Laboratory Base of Eco-Hydraulic Engineering in Northwest Arid Area, Xi'an710048, China)

Abstract:After dam experiences earthquake, the monitoring data of the dam body displacement will change promptly and obviously. The fitting is lower in degree and the result is poor in quality provided that the traditional statistic model is applied for building the model of the monitoring data. Therefore, the step function is introduced into the traditional statistic model and the regression analysis model is re-built. With the case of the monitoring data of the vertical displacement of Bikou dam, both the traditional statistic model and the step function model are applied for the stepwise regression analysis as well as the step function monitoring model is utilized to separate the earthquake component. Through analysis on the influence law of the earthquake to the vertical displacement of the dam, the superiority of the step function model is verified. The analysis demonstrates that the fitting precision and forecast effect of the step functional model both are higher than those of the traditional model. It provides similar projects with reference.

Key words:dam monitoring; step function; earthquake prompt change; stepwise regression analysis; earthquake component; statistic model

中图分类号：TV698.1

文献标识码：A

DOI:10.3969/j.issn.1006-2610.2016.02.021

基金项目：国家自然科学基金(51409205)；陕西省创新研究计划(2013KCT-15)

作者简介：陈容(1981- )，女，四川省隆昌县人，工程师，从事大坝运行管理工作.

收稿日期：2016-02-02

文章编号：1006—2610(2016)02—0080—05