氧化锆微型齿轮的粉末微注射成形数值模拟研究

何振宇 黎 力 龙继才 刘 琳

(中国矿业大学(北京)机电与信息工程学院 北京 100083)

氧化锆微型齿轮的粉末微注射成形数值模拟研究

何振宇 黎 力 龙继才 刘 琳

(中国矿业大学(北京)机电与信息工程学院 北京 100083)

微系统与其相关产品的蓬勃发展，使得市场对微型零件的需求急剧增加，而粉末微注射成形技术为其大规模生产提供了商业化的可能。重点研究了氧化锆陶瓷粉末-粘结剂微注射成形过程中三维充填模拟以及相关的实验验证。采用Power Law模型+Arrhenius模型，研究适于齿轮微注射成形用的注射温度。经研究发现，最适于齿轮微注射成形的注射温度为150 ℃。通过验证实验，Ansys-CFX软件模拟出来的结果能预测喂料的流变情况。

氧化锆陶瓷 齿轮粉末微注射成形 数值模拟 粘度方程

前言

近年来，粉末微注射成形技术愈来愈受到科研人员的关注，主要是由于它可近净成形具有复杂形状的纯金属、合金及陶瓷零件。与其它微制造技术相比，粉末微注射成形(简称μPIM)技术具有材料加工范围广、批量生产和低成本的优势，因此它更适合于制造陶瓷或金属微型零件[1]，是一种很有发展前景的微制造工艺。

粉末微注射成形主要分为4个步骤：混料、注射成形、脱脂和烧结[2]。由于粉末微注射成形通常是生产微尺寸结构产品，故而对原料、成形设备、注射成形和热处理工艺均提出了更为严格的要求，这也正是粉末微注射成形技术与传统粉末注射成形技术的主要区别之处[3]。

自20世纪90年代初虚拟制造技术出现以来，利用计算机进行模拟设计，得到最优设计后再进行生产，这样大幅缩短了产品生产周期,降低了费用,提高了产品质量[4]。数值模拟中描述单相流体的方程模型已经得到广泛研究，因陶瓷粉末注射成形喂料包含粉末和粘结剂，熔融的PIM喂料属于密相流，因此在将粘结剂处理为连续介质时，把粉末颗粒处理为拟流体，从而建立粉末-粘结剂双流体模型。这样既考察了粘结剂和粉末的流动行为，也省略了颗粒模型处理大量粉末颗粒的大规模计算，具有可行性。

1 实验过程与条件

1.1 喂料

实验采用平均粒径为0.8 μm，装载量为50 vol%的氧化锆粉末。粘结剂体系为蜡基粘结剂体系，其主要聚合物原料组分为：石蜡(PW)、乙烯-乙酸乙烯(醋酸乙烯)酯共聚物(EVA)、高密度聚乙烯(HDPE)、硬脂酸(SA)。

纯粘结剂的粘度方程Arrhenius模型[5]：

(1)

式中：E——材料粘性流动活化能，表示材料中温度对粘度的敏感程度,J/mol；

R——气体常数,8.314J/mol·K；

T——材料的温度,K；

η——T0温度下喂料的粘度值(Pa·s)，其粘度值与粘结剂本身剪切速率符合幂律关系；

T0——初始条件下的温度,K;

K——稠度系数。

在一定的温度和剪切速率下，纯粘结剂混合物的粘度η由对数叠加原理进行估算[6]：

(2)

式中:η——各个粘结剂成分的粘度值;

Wi——各成分的质量分数;

n——成分数目。

根据μPIM的拟流体假设，μPIM充模过程中的粉末本身具有粘度，且由于真实粉末与粘结剂体系的界面的复杂相互作用，使形成的等效粉末具有很高的粘度值。描述粉末等效粘度的模型有：

1)Cross模型[6]：

(3)

Powerlaw模型[6]：

(4)

式(3)、(4)中:η0——零剪切粘度，Pa·s;

τ*——零剪切粘度所对应的剪切应力,Pa；

m——与材料相关的常数；

n——非牛顿指数，当n=1时，表示该流体为牛顿流体。

本研究采用的粉末-粘结剂的粘度表达式：

(5)

式中：φp、φb——分别为粉末拟流体和粘结剂流体所占体积分数；

ηp、ηb、ηe——分别为粉末拟流体、粘结剂流体和喂料流体的粘度。

通过经验公式(1)、(2)、(3)、(4)、(5)可以得到等效粉末-粘结剂喂料的粘度值。

1.2 微齿轮充模流动的初始及边界条件

粉末注射成形充模模拟流动的初始条件是为处于t=0(充模开始)时各因素的加载状态。μPIM的充模流动边界条件见表1。

表1 μPIM的充模流动边界条件

1.3 粘度模型组合

Arrhenius模型与Cross模型的区别在于只是前者考虑温度变化对于粘结剂粘度值的影响，而后者则是考虑粘结剂流动过程中压力的变化对于粘结剂粘度值的影响。Power Law模型着重于描述喂料本身随剪切速率变化时对粘度的影响。根据实际工况和各模型特点，本实验采用的是Arrhenius模型+Power Law模型。

φpηp(PowerLaw)+φbηb(Arrhenius)=ηe

(6)

式中：m0——与材料有关的常数；

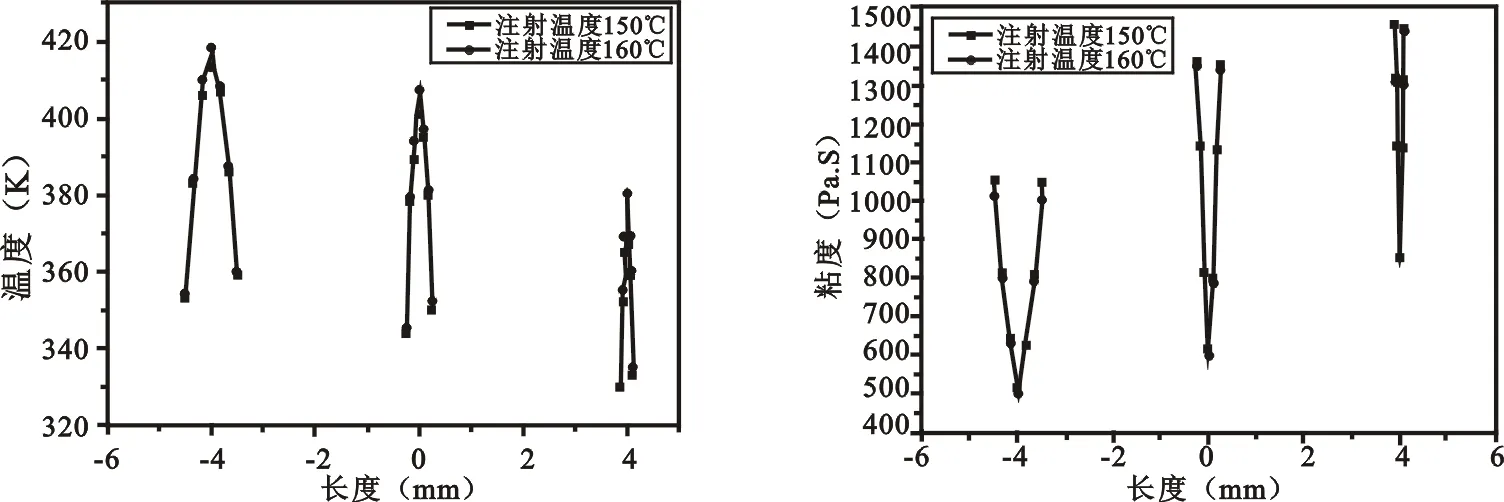
n——剪切稀化指数，0

2 结果与讨论

图1为不同的注射温度150 ℃、160 ℃粘接剂速度分布情况。由图1可以看出，注射温度为150 ℃、160 ℃时，流动的规律均为远浇口-近浇口，从模腔左边流向模腔右边的流动规律，当注射温度为160 ℃时流场分布不均匀，而注射温度为150 ℃时流场分布很均匀，这是因为粘结剂的粘度随着温度的升高而降低，粘度降低从而使得流动速度变大。

由图2可知，齿轮从左至右依次为φ1、φ0.5、φ0.2。由图2(a)可以发现，当注射温度为150 ℃、160 ℃时，对于φ1、φ0.5、φ0.2齿轮的温度场分布变化情况来说注射温度160 ℃时的温度略大于150 ℃；且对于齿轮温度分布为φ1>φ0.5>φ0.2。这同齿轮分布同浇口位置有关，随着齿轮距离浇口越远，粘结剂在传播中损耗的能量越多，表现在温度降低；也与比表面有关，齿轮越小比表面越大，热传导越多，温度越低。

图2(b)中粘度的规律与图2(a)中温度的规律相反，这是因为根据Arrhenius方程，粘度与温度之间呈负相关。从粘度值大小来看齿轮φ1<φ0.5<φ0.2处粘度值，这说明φ1成形最容易，φ0.2齿轮成形最难。在实际注射成形过程中，从理论角度应该优先考虑φ0.2齿轮成形。

(a)150 ℃ (b)160 ℃

(a)不同注射温度下温度场分布 (b)不同注射温度下粘度场分布

图3为不同注射温度下粉末-粘结剂速度差以及不同尺寸齿轮的PVF值(粉装量)分布。由图3(a)可以看出，随着齿轮直径的减小粘结剂同粉末的速度差值增加。图3(b)、图3(c)、图3(d)分别为φ1、φ0.5、φ0.2齿轮PVF值分布，从中可以发现，不同齿轮的PVF值随注射温度由150 ℃增至160 ℃时，整体上PVF值有所增加。当齿轮直径由φ1变为φ0.5时，可以看到最大粉装量由59.5%变为了65%，增加了5.5%。

综合上述在不同注射温度下，温度场、粘度场、速度差值、PVF值分布模拟结果，对于齿轮成形尤其是φ0.2齿轮成形，以及降低齿轮两相分离缺陷角度来说，注射温度为150 ℃最适宜齿轮成形。

(a)速度差分布 (b)φ1齿轮PVF值

(c)φ0.5齿轮PVF值 (d)φ0.2齿轮PVF值

图3 不同注射温度下齿轮速度差及各齿轮PVF值分布

Fig.3 Different injection temperatures of speed difference and the gear PVF value distribution

图4 注射温度为150 ℃时齿轮成形图

Fig.4 The SEM of gear under the injection temperature at 150 ℃

由图4、图5可以看出，注射温度为150 ℃时，φ1齿轮齿心圆成形良好，齿顶充填完整，表面粗糙度小，φ0.2齿轮表面粗糙度较大，但充填完整；注射温度为160 ℃时，φ1齿轮齿心圆成形良好，但齿顶圆出现凸起，φ0.2齿轮表面粗糙度很大，且齿顶圆充填不完整。从实际实验结果看，无论是φ1齿轮还是φ0.2齿轮，其注射成形均为150 ℃时成形质量均优于在160 ℃时成形质量，因此证明数值模拟得到的结果能很好地指导实践。

图5 注射温度为160 ℃时齿轮成形图

Fig.5 The SEM image of green of micro gear at 160 ℃

3 结论

笔者采用数值模拟，利用Arrhenius模型+Power Law模型考察了氧化锆粉末微注射成形充模过程中注射温度的影响，确定了150 ℃为最佳注射温度。最后在模拟的基础上，进行了粉末微注射成形实验来验证模拟结果，发现实验结果与模拟结果吻合，说明模拟设置模型及参数符合齿轮微注射成形使用Ansys-CFX模拟能准确预测及描述微齿轮成形的成形过程及成形质量情况。

1 Junhu Meng,Ngiap Hiang Loh,Bee Yen Tay,et al.Tribological behavior of 316L stainless steel fabricated by micro powder injection molding[J].Wear,2010,268(7～8):1 013～1 019

2 Liu Z Y,Loh N H,Tor S B,et al.Micro-powder injection molding[J].Jounal of Materials Processing Technology,2002,127(2):165～168

3 Tay B Y,Loh N H,Tor S B,et al.Characterisation of

micro gears produced by micro powder injection moulding[J]. Powder Technology, 2009, 188(3):179～182

4 胡忠. 材料加工过程计算机模拟的现状与未来[J].塑性工程学报,1998,5(2):1～8

5 Li Yimin,Khalil K A,Huang Baiyu.Rheological mechanical and corrosive properties of injection molded 17-4PH stainless steel[J].Trans Nonferrous Met Soc China,2004,14(5):934～939

6 蒋炳炎,许静静,谢磊,等.金属粉末注射成形W-Ni-Fe喂料粘度模型研究[J].机械科学与技术,2003,22(6):980～981

国家自然科学基金(项目编号：51304214)。

何振宇(1990-)，在读研究生；主要从事材料加工工程和陶瓷注射成形的研究。

刘琳(1978-)，副教授、硕士生导师，现任中国矿业大学(北京)材料系副主任；主要从事微钠制造、粉末微注射成形、材料成形过程的模拟仿真、表面强化技术及涂层材料的研究。

TF124

A

1002-2872(2016)05-0022-05