应用图像法的织物弯曲刚度计算
韩 蓉, 胡 堃, 毋 戈, 钟跃崎,2
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
应用图像法的织物弯曲刚度计算
韩 蓉1, 胡 堃1, 毋 戈1, 钟跃崎1,2
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
为评估虚拟服装所采用织物模型的准确性,有必要全面对比虚拟织物和真实织物的弯曲性能,因此提出采用图像法来计算织物的弯曲刚度。为采集织物在悬臂梁上弯曲形态的图像,设计了织物弯曲仪。真实织物在自重弯曲状态边缘存在翘曲现象,必须从翘曲织物的侧面形态中确定一条可以代表其弯曲性能的曲线。分别计算了翘曲织物上、下边缘曲线的弯曲刚度,提出采用中值曲线表示织物弯曲性能的方法。实验结果表明,通过中值曲线得到的弯曲刚度和KES法得到的弯曲刚度存在很好的线性相关度,且在45°和41.5°斜面上的测试结果具有很好的一致性。
图像处理; 织物翘边; 弯曲形态; 弯曲刚度; 中值曲线
Abstract To evaluate the accuracy of the fabric model used in virtual cloth, it is necessary to compare the bending properties between the virtual fabric and real fabric. A new method is proposed to test the bending property of woven based on image processing. An instrument has been made to collect the bending shape of woven fabrics under the cantilever beam tests. The real fabric bending under its own weight comprises warps which is inevitable in most cases. Therefore, certain curve selected from the side shape of curve fabric has to be proved suitable for representing the bending shape of the fabric. An approach of the mid-line representing the fabric′s bending properties has been developed after calculating the bending stiffness of fabric′s five different curve. This calculation and test method have been validated by experimental observations and correlation with KES test method. The results of tests on 45° and 41.5° inclined plane also reached a good consistency.
Keywords image processing; cloth warping edge; bending shape; bending stiffness; mid-curve
从20世纪80年代开始,虚拟试衣渐渐成为学术界研究的热点。虚拟试衣的核心技术是如何精确的对织物进行建模,模拟出栩栩如生的虚拟服装。基于物理建模的织物仿真建模工作经过二十多年的发展,主要涉及织物的力学模型[1],隐式积分方法的改进[2],基于包围盒以及基于GPU加速的碰撞检测分析与优化等。近年来,如何更精确地模拟织物非线性各向异性的力学响应特性是一个较为热门的方向。
基于现有织物模型和积分方法,虚拟服装是否能够准确的表达出服装的真实形态还没有定论。为解决这个问题,就必须对比真实织物和虚拟织物的力学性能。描述织物力学性能的指标有很多,其中织物的弯曲性能因对其服用性和风格有很大影响,故成为表征织物形态的重要指标。目前用于测量织物弯曲性能的仪器主要有硬挺度仪、FAST弯曲仪和KES-FB2弯曲仪等,硬挺度仪和FAST弯曲仪的测试原理是基于斜面法测出织物弯曲长度,该方法无法对虚拟织物弯曲性能进行评价。KES-FB2弯曲仪是通过测试织物弯曲曲率与外加力矩的关系,再计算弯曲刚度[3],该仪器较为昂贵,无法大面积推广。因此,有必要研究效果良好且性价比较高的测试仪器,用于衡量织物的弯曲性能,从而进一步地用于提高虚拟织物仿真建模的精度。
文献[4]提出了基于图像处理的织物弯曲性能测试方法,利用织物实际弯曲形态计算织物的弯曲性能。但其选取的试样都为不发生翘曲或翘曲很小的织物,即其算法是建立在织物边缘不发生翘曲的前提下。大量的观察发现,根据现有的国家标准和国际标准,斜面法测量织物弯曲时,由于内应力的作用,大多数织物在自然弯曲时边缘都会发生翘曲。而且实验证明一般的预处理并不能消除翘曲,较大程度的预处理如熨烫也不能完全消除翘曲,反而会影响织物的弯曲性能。故上述方法具有很大的局限性。
虽然上述方法存在缺陷,但也为本文提供了良好的思路。首先,斜面法测试简单、方便,无论是对虚拟织物进行模拟还是对真实织物进行操作都较易于实现。其次,图像法的采用可以分别得到虚拟织物和真实织物在自重下的自然弯曲形态,便于进行直观全面的对比,二者弯曲形态越相似,就表明虚拟织物采用的数学模型越准确。由于现有的虚拟织物大都基于质点弹簧模型,在自然弯曲时其侧面边缘并不会发生翘曲,而是一条平滑的曲线。为了采用上述方法实现虚拟织物与真实织物弯曲形态的对比,还必须从真实织物翘曲的侧面形态中找到一条可以代表其弯曲性能的曲线。
本文针对文献[4]的不足,设计加工了更加适用于图像采集的织物弯曲仪,采用图像法提取了织物上、下边缘及其中间的3条曲线并分别计算了这些曲线的弯曲刚度。与用KES测得的相同织物的弯曲刚度进行对比,分析了不同曲线形态和织物弯曲性能的关系。
1 试 验
1.1 试验仪器
织物弯曲仪:由于现有的织物弯曲仪并不适用于图像采集,故本文设计制作了便于图像采集和分析的织物弯曲仪,如图1所示。
弯曲仪具有41.5°和45°2个斜面,可以对比织物在不同斜角下的弯曲形态。斜面上标有刻度可以方便的读取织物的弯曲长度。弯曲仪后侧采用透明的有机玻璃板并装有照明装置,可以根据织物外观调整背景颜色及亮度,便于织物轮廓的提取。
数码相机(分辨率为1 800万像素),三脚架,KES-FB2织物弯曲仪。
1.2 试样制备
选用7种纯棉织物和6种涤/棉(60/40)混纺织物,参数如表1所示。依据GB/T 18318—2001《纺织品 织物弯曲长度的测定》,将这些织物分别按经、纬向裁剪成20 cm×2.5 cm的试样。测试前先将试样浸湿,然后放置于标准大气条件下24 h,轻压使其平整,以消除织物褶皱、折痕等对弯曲形态的影响。
1.3 图像采集及校正
测试时将织物试样的短边与弯曲仪的平台边缘对齐,盖上压板,推着织物向斜面方向缓慢移动。当织物的自由端接触到斜面时停止移动,用固定在三角架上的数码相机对其进行拍照。需要注意的是,为了消除透视形变的影响,拍照前要调整相机位置以保证弯曲仪的斜面和上平面重合为一条直线,如图2所示。图2(a)为斜面和上平面没有重合时的错误拍摄位置,图2(b)为斜面和上平面重合时的正确拍摄位置。

表1 织物参数
用13个试样分别在弯曲仪的41.5°和45°斜面上进行测试,共拍摄52张图像。因为相机镜头畸变的存在,拍摄到图像的尺寸、形状等会发生改变,还需对其进行校正才能进一步使用。本文选用GML Camera Calibration软件[5-7],先对相机进行标定,再对拍摄到的图像进行校正。以1号织物经向试样在45°斜面上的测试为例,给出校正后的图像如图3所示。
1.4 目标曲线的提取
从图3可以看出,即使进行了充分的预处理,织物在自然弯曲时边缘仍会发生翘曲。这并不是偶然现象,几乎所有的试样都存在这种现象。受纱线捻度、织物组织结构等因素的影响,不同织物在弯曲时发生翘曲的程度不同。由于翘曲的存在,从侧面看织物有上、下2条弯曲形态相差甚远的边缘,并且理论上在它们中间还存在着无数条代表织物弯曲形态的曲线。本文将上、下边缘及其中间的3条曲线作为目标曲线进行提取。提取目标曲线的主要流程为:1)提取织物图像轮廓;2)检测轮廓拐点;3)提取轮廓上、下边缘;4)计算上、下边缘间的3条曲线,分别命名为上四等分线,中值线和下四等分线。记上边缘曲线坐标为(x1i,y1i),i=1,2,…,M;下边缘曲线坐标为(x2i,y2i),i=1,2,…,N;则上四等分线的坐标为 (x3i=(3x1i+x2i)/4,y3i=(3y1i+y2i)/4),i=1,2,…,min(M,N);中值线的坐标为(x4i=(x1i+x2i)/2,y4i=(y1i+y2i)/2),i=1,2,…,min(M,N);下四等分线的坐标为(x5i=(x1i+3x2i)/4,y5i=(y1i+3y2i)/4),i=1,2,…,min(M,N)。本文以1号织物经向试样在45°斜面上的测试为例,给出织物图像的5条目标曲线,如图4所示。
1.5 弯曲刚度的计算
假设织物为弹性体,根据伯努利-欧拉理论,织物弯曲刚度与弯曲力矩、曲率之间的关系为
(1)
式中:B为弯曲刚度;M为弯曲力矩;K为曲率。
以目标曲线的自由端为原点建立直角坐标系,(xi,yi)为曲线上的点坐标,如图5所示。
在图5的坐标系下,曲线弯曲力矩(M)和曲率(K)分别可以表示为
(2)
(3)
式中:w为织物面密度;x′为x坐标轴上一点;θ为曲线段上当前点的切线与y轴的夹角;s为曲线线段长度;s′为x-x′对应的曲线。根据文献[4]的方法,可以计算曲线上任意点的弯曲力矩和曲率,进而得到曲线上任意点的弯曲刚度。
2 结果与讨论
2.1 目标曲线的弯曲刚度
本文通过MatLab编程实现了目标曲线任意点弯曲力矩和曲率的计算,以1号织物经向试样在45°斜面上的测试为例,结果如图6所示。
根据式(1)对弯曲刚度的定义,图6曲线上任一点的斜率就表示该点的弯曲刚度。可以看出,5条曲线的弯曲刚度都随着曲率的增加而逐渐减小,并渐渐趋于稳定,表现了织物弯曲刚度非线性的特点。可以观察到在曲率大于0.4后,所有曲线形态都近似为直线,为了避免弯曲刚度的微小波动,本文取曲率大于0.4的曲率和弯曲力矩曲线段的平均斜率作为其弯曲刚度,计算结果如表2所示。其中B1、B2、B3、B4和B5分别表示根据图像法求得的织物上边缘曲线、上四等分曲线、下四等分曲线、下边缘曲线、和中值曲线弯曲刚度。为了分析不同弯曲形态曲线和织物弯曲性能间的关系,采用KES-FB2织物弯曲仪测试了所有试样的弯曲刚度(Bk)。测试时将织物两端夹持,一端固定而另一端施加弯曲力矩发生弯曲变形,得到织物弯曲力矩与弯曲曲率间的变化关系,这种测试方法是纯弯测试,消除了剪切刚度对弯曲的影响。
2.2 相关性分析
本文是在斜面法的基础上利用织物弯曲形态计算织物的弯曲刚度,研究织物在重力作用下所受力矩对织物曲率的影响[8-9]。图像法测织物弯曲刚度与KES-FB2织物弯曲仪的理论是相同的,但并没有消除织物剪切对弯曲的作用,但在重力作用下织物的剪切变形非常微小,可以忽略不计。分别用表2中不同曲线的弯曲刚度B1、B2、B3、B4、B5和Bk进行相关分析,结果如图7所示。
从图7可以看出,B5与Bk相关性最好,线性相关系数R=0.888,说明在本文提取的5条目标曲线中,中值曲线的弯曲刚度(B5)与KES弯曲刚度(Bk)的变化规律最为相似,能够较好地用来计算织物的弯曲性能,它们之间的关系为Bk=0.613B5+0.000 2。这是由于织物边缘的纱线较为松动且受力不均匀,织物的剪切与弯曲变形往往是耦合的,中值曲线位于织物的中间位置,受交织纱线的作用力较为均匀,故其能够较好地反映织物在自重下弯曲的真实形态及性能。
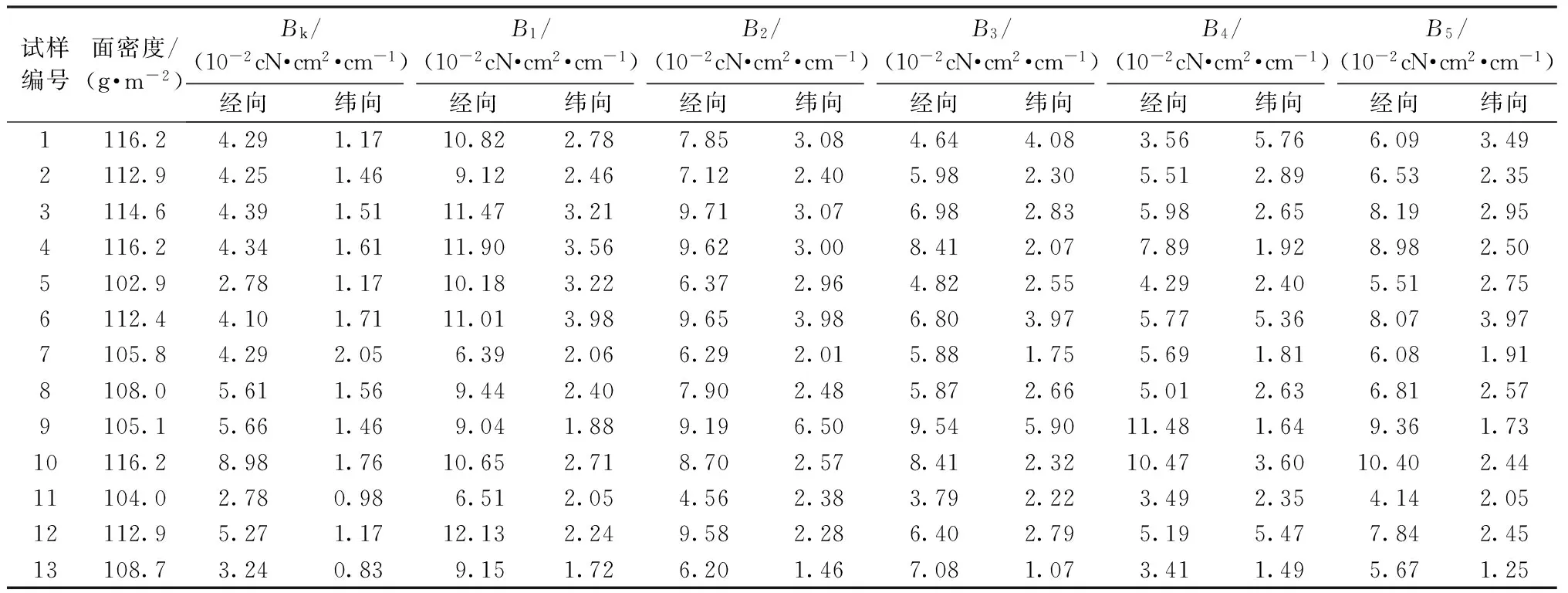
表2 弯曲刚度对比
2.3 不同斜面弯曲刚度的关系
本文采用织物弯曲仪设计了45°和41.5°2个斜面是为了丰富织物的弯曲形态以更好的与虚拟织物进行对比。为了分析织物弯曲形态和弯曲刚度之间的关系,对每种织物试样分别在45°和41.5°斜面上进行测试,并求出它们对应中值曲线的弯曲刚度B5(45)和B5(41.5)。对这2种斜面测试下的弯曲刚度进行相关分析,结果如图8所示。
从图8可以看出,B5(45)和B5(41.5)的相关系数为0.87,且拟合出的直线方程为B5(41.5)=1.17B5(45)+0.01,其斜率接近1,说明二者之间有着较好的一致性。
3 结 论
采用自主设计加工织物弯曲仪完成了基于图像处理计算织物弯曲刚度的完整算法,提出了采用中值曲线计算边缘存在翘曲织物的弯曲刚度的方法,得出以下结论:
1)绝大多数织物在自然弯曲时边缘都会在内应力作用下发生翘曲现象,且不易通过预处理消除。其原因在于织物的内应力是由织物结构和纱线性质决定的,故预处理对其影响有限。
2)对于边缘发生翘曲的织物,可以通过中值曲
线的弯曲刚度(B5)来表示其真实弯曲刚度,其与KES法得到的弯曲刚度(Bk)有着较好线性相关度,二者之间的关系为Bk=0.613B5+0.000 2。
3)同一织物在45°和41.5°斜面测试时,其弯曲形态的中值曲线所对应的弯曲刚度具有较好一致性。
[1] TERZOPOULOS D, PLATT J, BARR A, et al. Elastically deformable models[J]. ACM Siggraph Computer Graphics. ACM, 1987, 21(4): 205-214.
[2] VOLINO P, MAGNENAT-THALMANN N. Comparing efficiency of integration methods for cloth simulation[C]//Computer Graphics International 2001. Proceedings. [S.L.]: IEEE, 2001: 265-272.
[3] ZHOU N, GHOSH T K. On-line measurement of fabric bending behavior: part III: dynamic considerations and experimental implementation[J]. Textile Research Journal, 1999, 69(3): 176-184.
[4] 何琦辉, 王正伟. 利用织物实际弯曲形态测试其弯曲性质的算法[J]. 纺织学报, 2006, 27(12): 52-54. HE Qihui, WANG Zhengwei. Arithmetic of bending property of the fabric based on its actual bending shape[J]. Journal of Textile Research, 2006, 27(12): 52-54.
[5] KANG T J, JOO K H, LEE K W. Analyzing fabric buckling based on nonlinear bending properties[J]. Textile Research Journal, 2004, 74(2): 172-177.
[6] 石风俊,胡金莲. 织物的弯曲性能[J]. 纺织学报,2005,26(3):15-18. SHI Fengjun, HU Jinlian. Bending behavior of woven fabrics[J]. Journal of Textile Research,2000,26(3):15-18.
[7] 汪学骞,金世伟. 织物弯曲性能的测试及基本风格的分析[J]. 纺织学报,1999,20(5):270-273. WANG Xueqian, JIN Shiwei. Fabric bending performance test and the analysis of the basic style[J]. Journal of Textile Research, 1999,20(5):270-273.
[8] HODSON M. Woven fabric structure: US, Application, 11/559,994[P]. 2006-11-15.
[9] WANG Fumei, WU Xiongying. Study on the bending properties of woven fabrics and its yarns[J]. Journal of Donghua University, 2002, 19(4): 7-11.
Calculation on bending stiffness of woven fabrics by image processing method
HAN Rong1, HU Kun1, WU Ge1, ZHONG Yueqi1,2
(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLabofTextileScienceandTechnology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)
10.13475/j.fzxb.20141102206
2014-11-10
2015-08-20
上海市自然科学基金资助项目(14ZR1401100)
韩蓉(1990—),女,硕士生。研究方向为基于图像处理的织物弯曲仪的研制。钟跃崎,通信作者,E-mail:zhyq@dhu.edu.cn。
TS 941.2
A

