基于仿射传播聚类算法的广义负荷稳态特性建模及其应用

褚壮壮 ，梁 军 ，张 旭 ，董晓明 ，张永亮

（1.山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061；2.国网济南市供电公司，山东 济南 250012；3.国网滨州市供电公司，山东 滨州 256600）

0 引言

大规模新能源并网对电力系统安全稳定运行造成很大冲击，可再生能源发电的接入改变了电力网络节点的功率传输走向及其特性，特别是分布式新能源的不断涌现，使传统的负荷节点向电网倒送功率成为可能［1］。因此，含新能源的广义负荷建模是对传统负荷建模在新场景下的发展和延伸。新能源具有随机波动性、间歇性，而负荷本身具有时变性，这两者的相互作用加剧了广义负荷节点的不确定性，对系统潮流分布、仿真计算、电网安全运行等会产生较大影响［2-5］，因此考虑风电随机波动性的广义负荷节点特性建模对电力系统分析具有重要意义。

传统建模方法采用分类与综合的思想，通过总体测辨法得到负荷的准确模型，拟合效果较好［6-13］，推进了负荷建模工作的发展和应用。其中文献［6］首次提出了动态负荷特性的分类与综合问题，并提出了基于系统回响辨识和基于模型回响辨识的动态负荷特性综合办法；文献［7］以标准电压激励响应和负荷有功运行水平作为特征向量，采用KOHONEN神经网络映射到高维空间进行分类；文献［8］对K-means聚类算法进行改进并定义了评估指标，以此进行负荷聚类分析；文献［9］运用模糊聚类方法给出了长沙主要变电站的分类结果；文献［10］通过日负荷最大、最小负荷率构造分类判据，将特殊负荷分为电解铝类负荷和铁合金类负荷，并分别对2类特殊负荷模型进行验证；文献［11］以感应电动机综合负荷模型参数和动态负荷所占比例为特征向量，提出了基于模糊C均值聚类的负荷特性分类方法，采用直接综合和加权平均综合2种综合方法对分类结果进行综合建模；文献［12］以各负荷节点-变电站的不同类型负荷比例为特征向量，运用基于模糊等价关系的传递闭包法对实测数据进行了模糊分类；文献［13］建立山峰密度函数自适应确定聚类数和聚类中心。

传统负荷建模聚类方法处理负荷的时变性效果较好，但其采用的聚类方法需人为设定聚类数、聚类中心等，较为主观，在考虑风电接入的复杂场景下不具有普遍适用性。由于风电接入规模的不断扩大，渗透率逐渐增加，改变了传统负荷节点单纯消耗功率的情况，使得负荷节点组成成分和功率流向发生本质改变，传统简单聚类策略及聚类方法对新场景下由风电和负荷叠加产生的复杂数据进行合理聚类存在不足，因此研究考虑风电接入新场景下广义负荷不确定性的合理聚类与综合以及建模成为亟待解决的问题。

为解决上述问题，本文提出基于仿射传播AP（Affinity Propagation）聚类算法的广义负荷稳态特性的聚类与综合方法。该聚类算法属于无监督聚类算法，因特殊的消息传递机制与竞争机制自适应确定聚类数，能够自动消除聚类振荡并自动寻找最优聚类结果，面对复杂场景，聚类质量高，效果明显。首先对节点根母线功率数据进行特征分析，利用动力学的波动强度理论选取功率波动序列的最小时间长度，然后以时段序列内各最小时间长度的波动强度以及时段序列的数字特征为指标构造特征向量，利用日时段特征向量作为聚类指标，应用AP聚类算法自适应调整样本数据的聚类数和聚类中心。采用依概率分区间的广义负荷建模方法［14］，利用RBF神经网络对各类样本数据建立概率广义负荷模型，并通过模式验证判断测试样本所属类别，以确定待测试样本属类并检验该聚类方法的有效性。通过仿真算例与K-means算法对比，说明AP聚类算法聚类质量优越，解决了K-means聚类随机初始聚类中心导致的聚类结果不稳定问题。最后将聚类后的模型应用于风电接入后的风险分析仿真计算，验证了本文方法的实用性，可为系统决策提供参考。

1 AP聚类算法描述

传统负荷建模领域通常采用K-means聚类算法［15-16］、模糊神经网络聚类算法［7-8，11］等，大部分需人为设定聚类数和聚类中心等，主观因素较强，不具备客观普遍性，因此本文引入AP聚类算法［17］。AP聚类算法是一种新的无监督聚类算法，无需事先定义类数。算法开始时把所有的数据点均视作类中心，通过数据点间的“信息传递”来实现聚类过程。在迭代过程中不断搜索合适的聚类中心，自动从数据点间识别聚类中心的位置及个数。AP算法是在数据点的相似度矩阵上进行聚类的，聚类的目标是使数据点与其聚类中心之间的距离达到最小，因此选用欧氏距离作为相似度的测量指标，即任意2个向量Xi和Xk的相似度为：

在聚类之前，每个数据点被赋予偏向参数P（i）=S（i，i），表示数据点 i被选作聚类中心的倾向性，该值越大则聚类数越多。AP聚类算法用代表矩阵［r（i，k）］（responsibility）和适选矩阵［a（i，k）］（availability）来表示数据点之间的 2 类信息，其中 r（i，k）是从 Xi指向候选聚类中心Xk，它反映了Xk适合作为Xi的聚类中心所积累的证据，该值越大表明候选聚类中心k成为真正聚类中心的可能性越大；a（i，k）从候选聚类中心Xk指向Xi，它反映了Xi选择Xk作为其聚类中心的合适程度所积累的证据，如图1所示。在邻近传播结束时，Xi的聚类中心确定为Xk，k满足：

图1 AP算法消息传递机制Fig.1 Message transfer mechanism of AP algorithm

基于AP算法的聚类过程具体计算步骤如下。

a.初始化。确定样本点数N、迭代次数M、聚类样本数据的特征向量，按式（1）计算N个样本点的相似度矩阵S作为输入量，其中对偏向参数P赋值，初始化r和a为0。

b.计算各点间 r（i，k）和 a（i，k）。

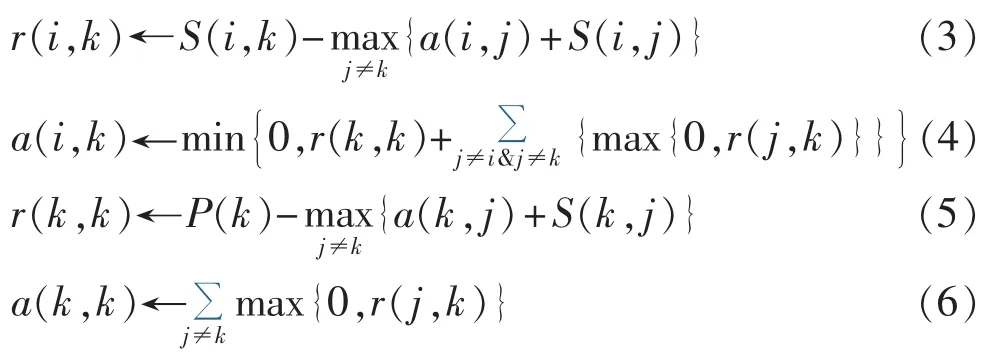
c.由于AP聚类过程中容易产生振荡，因此通过设定阻尼系数λ来控制迭代速度，循环迭代更新r和a，如式（7）和（8）所示。

d.迭代满足式（2）所确定的k点，则k为样本点i的聚类中心。如果迭代次数超过设定的最大值或者当聚类中心在若干次迭代中不发生改变时终止计算，确定类中心及各类的样本点；否则返回步骤b继续计算。

2 基于日时段功率空间的特征向量

在传统负荷聚类与综合研究中，负荷场景简单，通过简单的聚类方法以及聚类策略进行聚类就可将样本数据区分不同的类别，而大规模风电接入负荷侧后，由于负荷时变性与风功率波动性相互叠加，节点呈现的特性包括幅值和流向具有随机性，场景更为复杂，需提出新的指标作为评价标准。广义负荷节点有功功率因其能够可靠表征节点特性、变化范围大、易于细化分段的特点，不但可定性分析节点呈现负荷特性还是电源特性，还可以将其定量细化到具体功率范围，因此以节点有功功率作为节点特性特征参数，通过时段细化节点功率空间，以时段内各最小时间长度的样本波动强度序列以及时段内样本数据统计量为指标构造日时段特征向量进行聚类分析。

2.1 波动强度概念

为构建聚类所需的特征向量，引入场均速度、波动速度和波动强度的概念。波动强度（fluctuation intensity）是动力学领域的一种统计物理概念［18］，可以表征信号序列曲线的波动程度，定义为波动速度的均方根与场均速度的比值，某一段序列波动强度越小则信号波动越小，反之波动越剧烈。

波动强度数学表达式为：

其中，γ 为波动强度；为场均速度；P′（t）为波动速度；K 为样本序列的点数；Tt为采样周期；p（i）为样本序列各点值。

2.2 波动强度最小时间长度

定义波动强度最小时间长度T为能保持该时段内广义负荷母线功率近似不变的最小时间段，为此该值的选取应满足在T内波动强度变化率不超过规定的变化率阈值，则近似认为该时段内近似功率不变，可将本时间长度内功率波动值作为特征向量的元素；同时为保证聚类数合适，最小时间长度不能过小，故T应取满足式（10）的最小值。

其中，tmin和tmax分别为采样时间和样本总体时间；t为待定时间长度，取采样时间的倍数，以分钟计；Nt为不大于采样样本数的自然数；φti为待定时间长度t内，采样样本序列i的功率波动强度；T为满足约束条件max｛φti｝＜σ的最小时间长度；P为负荷与风电组成的广义负荷根母线有功功率序列；av为待定时间长度t下，采样序列i的有功功率均值；j、k为功率序列号；σ为变化率阈值。

2.3 聚类特征向量

将全部训练样本数据按聚类时间间隔TJ统一分段。聚类时间间隔TJ由多个T组成，利用TJ内每个最小时间长度T内样本的变化波动序列表征数据波动趋势，并和实际有功功率统计量构成特征向量Wp：

其中，p为聚类时间间隔序列号；b为TJ中包含最小时间长度T的序列数；Wmaxp和Wminp分别为第p个聚类时间间隔内的最大有功功率和最小有功功率；p为第p个聚类时间间隔内有功功率的均值；φp1、φp2、…、φpb为TJ内b个最小时间长度波动强度序列。以φpi为例，其计算式如下：

其中，i为TJ中最小时间长度序列号；P为负荷与风电组成的根母线有功功率序列；j为广义负荷有功功率序列标号；为最小时间长度序列i内功率均值。

由波动强度序列计算公式可知，其幅值大小充分反映广义负荷节点功率波动的幅度，其值正负反映广义负荷节点功率的流向，因此以各最小时间长度内样本的波动强度序列为基础所构造的特征向量作为聚类指标可以合理区分不同时段广义负荷节点特性。

3 基于概率标识的广义负荷建模

通过构造日时段的特征向量并利用AP聚类算法可以获得复杂场景样本数据聚类结果，但如何得到每类数据的广义负荷模型以验证聚类效果，需采用广义负荷特性综合的方法。由于风电接入使得广义负荷节点的功率流向和幅值大小呈现不确定性，传统建模方法不具备随机特征描述能力，难以应用于风电接入不确定场景下的建模分析，因此本文采用带有概率信息的广义负荷建模进行聚类验证。

3.1 节点特性提取

针对风电接入后节点功率流向的改变，有功功率因其能够可靠表征节点特性、变化范围大而被选作节点特性参考变量。以消耗功率或发出功率为依据，将节点特性划分为负荷特性或电源特性；针对节点特性的不确定性变化，对有功功率样本空间进行自适应分段并统计其概率分布；对有功功率依据特性自适应划分区间，利用RBF神经网络法学习并提取各区间节点特征。

RBF神经网络是多维空间插值的传统技术，可以经过每个样本点，能够逼近任意的非线性函数，处理难以解析的规律性，具有良好的泛化能力和全局逼近能力，并有很快的学习收敛速度，克服了BP神经网络存在的局部最小值和收敛速度慢的缺陷［19］，因此本文采用RBF神经网络作为节点特性提取的模型。模型结构由输入层、隐含层和输出层组成，其网络结构如图2所示。

该网络从输入层到隐含层为非线性映射，隐含层到输出层为线性映射。隐含层径向基函数通常选用高斯核函数。RBF神经网络属于前向型神经网络，其结构具有自适应性，且输出与初始权值无关。相比其他前向型网络，RBF网络具有结构简单、训练简洁、收敛速度快、逼近性能好、需设置参数少等特点，因此被广泛应用于非线性优化、时间序列预测和模式识别等科学领域。

图2 RBF神经网络结构Fig.2 Structure of RBF neural network

本文采用RBF神经网络函数对区间样本进行模型特征提取。其中，输出变量为有功功率p，输入变量为节点电压u，表达式如式（13）所示：

其中，wr为输出层连接权值；M为区间样本个数；Rr（u）为第r层隐含层径向基函数。

计算模型结构如下：

其中，k为输出变量序号；n为输入变量序号；m为节点分段功率区间编号；Em为区间样本训练误差；Nm为区间样本数；No为输出神经元个数；Pk，n为区间样本功率实测值；pk，n为模型计算值；Xn为输入变量向量；Cj、δj分别为第j个隐含层神经元的中心和扩展常数；Nh为隐含层神经元的个数；wj，k为第j个输出变量与第k个隐含层神经元的连接权值；Ni为输入层神经元个数。

采用梯度自适应调整算法求解模型参数，调整公式为：

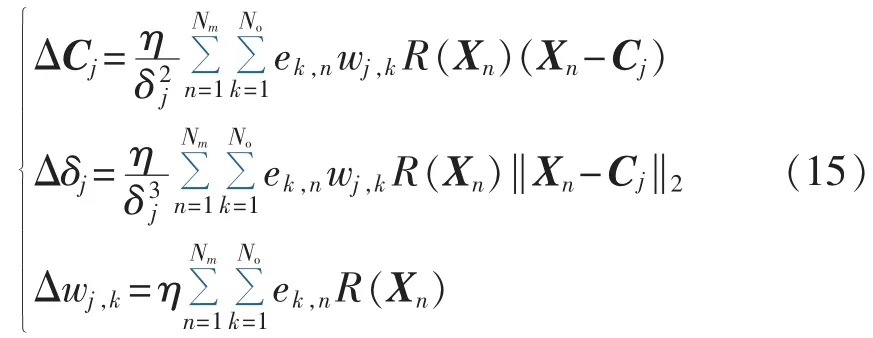
其中，ΔCj为误差对隐含层中心的调整参数；Δδj为误差对隐含层扩展常数的调整参数；Δwj，k为误差对隐含层输出权值的调整参数；η为训练学习系数。

3.2 模型结构

每类合并各段模型，形成如式（16）的统一模型结构。

其中 ，imid=10Pmin/Pbase，imax=10Pmax/Pbase，Pmin、Pmax分 别为节点电源特性功率最小值和最大值，Pbase为基准功率（本文中取风场基准功率 100 MW）；分别为各段下提取的电源特性和负荷特性关系表达式；为各段中根母线电压；i为分段区间标识；s表示电源特性区间；l表示负荷特性区间；Ps、Pl分别为电源特性区间和负荷特性区间的概率信息。

该基于概率标识的广义负荷建模方法充分考虑了风电接入复杂场景下节点特性呈现不确定性，解决了传统建模方法无法描述节点特性随机变化的问题。通过该建模方法，不但可以获得聚类后各类别的精确广义负荷模型，还可通过测试样本泛化以检验聚类的合理性与有效性。

3.3 聚类建模流程图

通过时段序列内各最小时间长度的波动强度以及时段序列的数字特征为指标构造特征向量，采用AP聚类算法对时段样本数据进行聚类，然后对每个类别内样本数据，利用RBF神经网络按照依概率分区间的方法建立节点特性统一模型，流程图如图3所示。

图3 聚类建模流程图Fig.3 Flowchart of clustering and modeling

4 算例验证及分析

本文风电数据采自2011年某月山东某沿海风场实测有功运行数据，负荷数据为该地某变电站110 kV侧出线的功率数据。取该月前25天数据为训练样本，后5天数据为测试样本，采样间隔均为5 min。利用风电场有功出力数据采用定功率因数的方式获得无功功率，与负荷叠加获得根母线功率，将根母线广义负荷节点视为PQ节点，并作为New England 39节点算例系统中母线16的功率数据，其他负荷母线功率数据满足以算例系统标准值为期望值、标准值的5%为标准差的正态分布，通过潮流计算获得母线16的电压样本，以此获得聚类与建模所需数据。

4.1 节点时段特性聚类分析

首先据式（10）确定待定时间长度内最大波动强度，结果如表1所示。

表1 待定时间长度内最大波动强度Table1 Maximum fluctuation intensity of candidate time lengths

文中合理选择波动变化率阈值σ为0.2，所以满足阈值限制的最小时间长度为15 min。

考虑聚类结果可靠性与模型的实用性因素，聚类时间间隔TJ取4 h，则单日被分为6个连续时段。以2011年某月前25天数据为训练样本，则训练样本按时间顺序共分为150个时段，构造特征向量进行聚类，结果如表2所示。

由表2可以看出，训练样本数据自动划分为4类，聚类中心分别为第 33（类别 1）、57（类别 2）、61（类别3）和78（类别4）段，其中数字为训练样本所划分时段序列数。由表2可知连续2天的时段特性也不尽相同，主观高峰低谷时段的划分方法不适用于风电接入的广义负荷场景，因此利用本文聚类方法充分统筹日时段的差异性和趋同性。

为充分说明AP聚类算法效果的优势，与传统K-means聚类算法进行对比。由于AP聚类算法自适应将训练样本分为4类，因此设定K-means算法的聚类数为4。为定量分析2种算法的聚类效果，定义评价函数E如下：

其中，E是全部样本点到所属类别聚类中心的总距离平方和；Xi为所属类别中心Cj的样本点；mCj为类别Cj的聚类中心；Nk为样本类别总数；NC为所属类别Cj的样本点Xi数量。计算结果如表3所示。

表2 聚类结果Table 2 Results of clustering

表3 AP算法与K-means算法聚类效果对比Table 3 Comparison of clustering effect between AP and K-means methods

其中，AP聚类算法与K-means聚类算法的距离平方和E分别为28.0350和42.9685，显然采用AP算法聚类后各类内样本点与聚类中心距离更近，聚类效果更好。K-means依赖于初始聚类中心的随机选择，若初始聚类中心选择不合理，聚类结果往往较差。同时，K-means算法对于离散和噪声数据比较敏感，少量此类数据就可产生较大影响，不适应于对负荷广义复杂场景下差别大、数据量大、较分散的样本进行聚类，而且需要聚类前人为规定聚类数目，较为主观，不能客观反映数据的类别属性。而AP算法不受离散和噪声数据影响，适用于大数据样本下的聚类，也无需规定聚类数，避免了主观影响，能够在数据本质属性规律的基础上，实现无监督、自适应聚类，结果更为客观。

4.2 聚类广义负荷建模分析

利用上文聚类方法得到样本数据的4类聚类结果，对每类数据以概率分区间分别建立广义负荷稳态模型，为保证样本数据充足，需利用各类中全部实测样本数据，限于篇幅仅呈现类别3的拟合效果以证明该方法描述能力，如表4和图4所示。

表4 类别3概率分布与拟合误差Table 4 Probability distribution and fitting error of Cluster 3

图4 类别3拟合图Fig.4 Fitting diagram of Cluster 3

由表4可知，本文选用的建模方法拟合误差较小，最大误差为 1.006×10-3，出现在区间［0.5，0.6），拟合效果较好。图4描述了类别3数据的整体拟合效果（纵轴有功功率为标幺值，后同），整体误差为6.743×10-4，仅在个别点处略有偏差，整体拟合效果较好，验证了本文聚类方法的有效性。

4.3 测试样本识别验证

为验证聚类结果正确性，取测试样本中某天的全部时段进行验证，通过构建特征向量，分别与训练样本聚类生成的聚类中心的特征向量按式（18）进行欧氏距离计算，结果如表5所示。

其中，ρ（Xj，Xc）为测试样本 Xj与聚类中心 Xc的欧氏距离；Nn为向量Xj与Xc所包含的元素个数。

表5 测试样本与各聚类中心欧氏距离Table 5 Euclidean distance between test sample and cluster center

由表 5 可知，测试时段 1、2、5、6 属于类别 4，而测试时段3、4属于类别2。分类结果表明，一天内各时段特性也不尽相同，这是由于不同时段内广义负荷母线风电随机波动性与负荷时变性叠加相互作用而使广义负荷所表现出的功率特性不同，从而产生了负荷母线特性的时段差异性。为充分验证聚类方法的有效性，分别用4类模型对测试样本时段3进行拟合，拟合效果如图5所示。

图5 待检验时段拟合效果Fig.5 Fitting effects of different models

可知，4 类模型拟合误差分别为 0.2967、4.3×10-4、0.3342、9.86×10-4。显然，利用类别2拟合效果较好，类别4拟合效果次之，类别1、3拟合脱离测试样本实测值，误差大，通过特性综合再次证明了本文提出聚类方法的正确性。用本文方法与传统最小二乘法［20］对训练样本中某天数据进行建模，拟合效果如图6所示。

图6 本文方法与传统建模方法结果比较Fig.6 Comparison between proposed and traditional modeling methods

可见，当广义负荷节点功率特性变化波动剧烈时，传统方法难以准确拟合，而本文方法先对数据进行聚类处理，利用同类数据建立广义负荷模型，建模结果更加精确。

5 基于AP聚类算法的广义负荷稳态建模在风险分析中的应用

针对日时段样本经过本文所提出聚类方法聚类后得到的广义负荷聚类类别信息，引入带有概率信息的RBF神经网络模型进行建模，能够在反映节点时段特性的基础上对不确定问题进行全局描述。因此，从风险评估角度综合考虑支路潮流临近度、节点电压临近度和场景发生概率，分析系统在稳态运行情况下的潜在风险。

本文以IEEE 5节点系统为例，将前文建立的4类广义负荷概率模型分别作为母线3的节点特性模型，修正功率不平衡量如下：

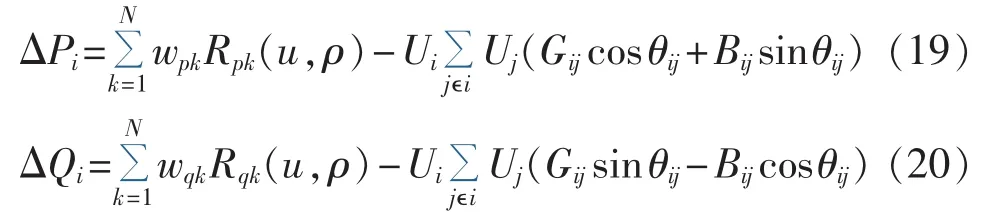
其中，N为区间样本数；u为节点电压输入量；wpk和Rpk（u）分别为求解有功修正量时第p个输出层连接权值和第p个隐含层径向基函数；wqk和Rqk（u）分别为求解无功修正量时第q个输出层连接权值和第q个隐含层径向基函数；Ui和Uj分别为节点i和节点j处的电压值；Gij、Bij和θij分别为线路电导、电纳和节点电压相角差。

按式（19）和（20）分别修正雅可比矩阵中对角元素，分别进行类别内各分段功率场景下的潮流计算，获取支路潮流和节点电压，定义支路潮流失稳临近度Pc和节点电压失稳临近度指标Uc考核系统运行的潜在风险。根据风险评估定义，风险度指标δP、δU为发生可能性与严重度乘积，如式（21）所示。

其中，Pmn为支路功率；分别为支路功率上、下限，分别为 2.5、-2.5 p.u.；U 为节点电压；Umax、Umin分别为节点电压上、下限，分别取 1.1、0.9 p.u.；Pm为类内功率区间m出力概率，即发生的可能性指标。

根据式（21），限于篇幅以类别4为例，风险分析结果如表6所示。

表6 节点3电压风险评估Table 6 Voltage risk assessment for node 3

表6从节点电压的角度，综合考虑Uc与功率区间发生可能性 Pm，得出其风险度 δU，其中［0，0.1）、［0.1，0.2）的 δU分别为 0.0172、0.015；表 7 从支路潮流角度，综合考虑Pc与功率区间发生可能性Pm，得出其风险度 δP，其中［0.2，0.3）、［0.3，0.4）的 δP分别为0.0569、0.0891。因此，当出现上述功率区间时应通过调度控制措施避免系统越限而造成损失。

表7 母线2、3间支路潮流风险评估Table 7 Power flow risk assessment for branch between bus 2 and bus 3

对于文中广义负荷聚类形成的4个类别，根据式（22），综合考虑每个类别内的每个功率区间对节点电压的影响进行风险分析统计。

其中，Pi，m为类别 i第 m 个功率区间概率值；为类别i内第m个功率区间电压失稳邻近度；Ni为类别i的功率区间分段数；为类别i的整体电压风险度。

对4类聚类类别中节点3风险分析结果进行对比，如表8所示。

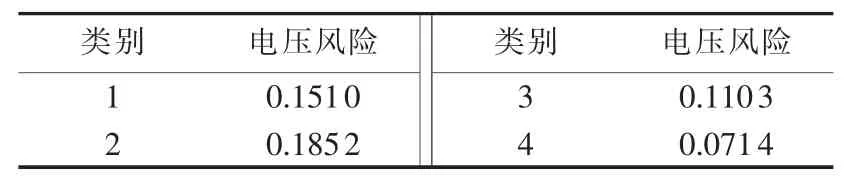
表8 风险分析对比Table 8 Comparison of voltage risk

由表8分析可知，类别2总体电压风险较高，这是由于类别2内风电接入水平较高，系统不确定性因素较强，节点越限风险大。因此，当判别时段特性样本归属于类别2时，应特别注意，否则易引起系统运行偏差，从而带来经济、安全隐患。

6 结论

本文将客观的、适用于复杂数据场景的AP算法应用于电力系统广义负荷特性聚类，通过实测样本空间的直观聚类结果与特性综合，并与K-means聚类算法比较，说明了该算法的有效性和优越性。

a.提出了按时间段划分并以时段内波动强度序列以及统计量构造特征向量的聚类方法。该聚类方法能够反映样本数据的日时段特性规律，不仅可以充分反映日时段内的差异性和趋同性，而且可以直观表达日间节点特性的差异性。

b.通过模式匹配判断样本所属类别，利用广义负荷建模检验聚类有效性。仿真结果表明，测试样本采用所属类别的模型拟合效果较好，因此通过本文AP聚类后综合能够得到精确广义负荷模型。

c.将聚类后综合得到精确广义负荷模型应用于风电接入后的风险仿真计算分析，结果指出了高风险节点功率区间，可为系统决策提供参考。

［1］李欣然，惠金花，钱军，等.风力发电对配网侧负荷建模的影响［J］. 电力系统自动化，2009，33（13）：89-94.LI Xinran，HUI Jinhua，QIAN Jun，et al.Impact of wind power generation on load modeling in distribution network［J］.Automation of Electric Power Systems，2009，33（13）：89-94.

［2］孙东磊，韩学山，李文博.风储共存于配网的动态优化潮流分析［J］. 电力自动化设备，2015，35（8）：110-117.SUN Donglei，HAN Xueshan，LI Wenbo.Analysis of dynamic optimal power flow for distribution network with wind power and energy storage［J］.Electric Power Automation Equipment，2015，35（8）：110-117.

［3］ENGELHARDT S，ERLICH I，FELTES C，et al.Reactive power capability of wind turbines based on doubly fed induction generators［J］.IEEE Trans on Energy Conversion，2011，26（1）：364-372.

［4］黄学良，刘志仁，祝瑞金，等.大容量变速恒频风电机组接入对电网运行的影响分析［J］. 电工技术学报，2010，25（4）：142-149.HUANG Xueliang，LIU Zhiren，ZHU Ruijin，et al.Impact of power system integrated with large capacity of variable speed constant frequency wind turbines［J］.Transactions of China Electrotechnical Society，2010，25（4）：142-149.

［5］杨悦，李国庆，王振浩.基于可信性理论的含风电电力系统电压稳定概率评估［J］. 电力自动化设备，2014，34（12）：6-12.YANG Yue，LI Guoqing，WANG Zhenhao.Probabilistic voltage stability assessment based on credibility theory for power system with wind farm［J］.Electric Power Automation Equipment，2014，34（12）：6-12.

［6］章健.电力系统负荷建模方法的研究［D］.北京：华北电力大学，1997.ZHANG Jian.Studies on modeling methodology of electric loads［D］.Beijing：North China Electric Power University，1997.

［7］张红斌，贺仁睦，刘应梅.基于 KOHONEN 神经网络的电力系统负荷动特性聚类与综合［J］. 中国电机工程学报，2003，23（5）：1-5.ZHANG Hongbin，HE Renmu，LIU Yingmei.The characteristics clustering and synthesis of electric dynamic loads based on KOHONEN neural network［J］.Proceedings of the CSEE，2003，23（5）：1-5.

［8］白雪峰，蒋国栋.基于改进K-means聚类算法的负荷建模及应用［J］. 电力自动化设备，2010，30（7）：80-83.BAI Xuefeng，JIANG Guodong.Load modeling based on improved K-means clustering algorithm and its application［J］.Electric Power Automation Equipment，2010，30（7）：80-83.

［9］李培强，李欣然，陈凤，等.模糊聚类在统计综合法负荷建模中的应用［J］. 电力自动化设备，2003，23（5）：43-45.LI Peiqiang，LI Xinran，CHEN Feng，et al.Application of fuzzy clustering in component-based modeling approach［J］.Electric Power Automation Equipment，2003，23（5）：43-45.

［10］鞠平，王耀，项丽，等.考虑特殊负荷的宁夏电网负荷建模［J］.电力自动化设备，2012，32（8）：1-4.JU Ping，WANG Yao，XIANG Li，et al.Load modeling for Ningxia grid special loads［J］.Electric Power Automation Equipment，2012，32（8）：1-4.

［11］鞠平，金艳，吴峰，等.综合负荷特性的分类综合方法及其应用［J］. 电力系统自动化，2004，28（1）：64-68.JU Ping，JIN Yan，WU Feng，et al.Studies on classification and synthesis of composite dynamic loads［J］.Automation of Electric Power Systems，2004，28（1）：64-68.

［12］黄梅，贺仁睦，杨少兵.模糊聚类在负荷实测建模中的应用［J］.电网技术，2006，30（14）：49-52.HUANG Mei，HE Renmu，YANG Shaobing.Application of fuzzy clustering in measurement-based load modeling［J］.Power System Technology，2006，30（14）：49-52.

［13］李培强，李欣然，陈辉华，等.基于减法聚类的模糊神经网络负荷建模［J］. 电工技术学报，2006，21（9）：2-6.LI Peiqiang，LI Xinran，CHEN Huihua，et al.Fuzzy neural network load modeling based on subtractive clustering［J］.Transactions of China Electrotechnical Society，2006，21（9）：2-6.

［14］张旭，梁军，贠志皓，等.考虑风电接入不确定性的广义负荷建模［J］. 电力系统自动化，2014，38（20）：61-67.ZHANG Xu，LIANG Jun，YUN Zhihao，et al.Generalized load modeling and application considering uncertainty of wind power integration［J］.Automation of Electric Power Systems，2014，38（20）：61-67.

［15］WANG Z，BIAN S，LIU Y，etal.The load characteristics classification and synthesis of substations in large area power grid［J］.International Journey of Electrical Power& Energy Systems，2013（48）：71-82.

［16］ORDONEZ C，OMIECINSKI E.Efficient disk-based K-means clustering for relational databases［J］.IEEE Transactions on Knowledge and Data Engineering，2004，16（8）：909-921.

［17］FREY B J，DUECK D.Clustering by passing messages between data points［J］.Science，2007，315（5814）：972-976.

［18］张学清，梁军，董晓明.基于累积指数的电网电压稳定性能的评估［J］. 电工技术学报，2012，27（7）：235-241.ZHANG Xueqing，LIANG Jun，DONG Xiaoming.An assessment for voltage stability performance of power grid based on cumulating index［J］.Transactions of China Electrotechnical Society，2012，27（7）：235-241.

［19］翟学锋，卫志农，范立新，等.基于相关向量机的发电机进相能力建模［J］. 电力自动化设备，2015，35（3）：146-151.ZHAI Xuefeng，WEI Zhinong，FAN Lixin，et al.Generator leading phase capability model based on relevance vector machine［J］.Electric Power Automation Equipment，2015，35（3）：146-151.

［20］徐兵.基于在线数据的负荷建模研究［D］.济南：山东大学，2013.XU Bing.Research on load modeling based on on-line data［D］.Ji’nan：Shandong University，2013.