微电网黑启动中考虑负荷恢复优化的分布式电源恢复方案

刘 仲，牟龙华，许旭锋

（同济大学 电气工程系，上海 201804）

0 引言

微电网黑启动，是指在整个微电网因外部或内部故障停运进入全黑状态后，不依靠大电网或其他微电网的帮助，仅通过启动微电网内部具有黑启动能力的分布式电源（DG），进而带动微电网内无黑启动能力的DG，逐步扩大系统的恢复范围，最终实现整个微电网的恢复［1］。微电网黑启动过程一般包括3个阶段，即DG恢复、网架重构和负荷恢复［2］。其中，DG恢复是整个恢复过程的基础，而负荷恢复则是黑启动的最终目的。

一些学者对传统电网黑启动的各个阶段进行了详尽的研究。在机组恢复方面，文献［3］提出了多目标的优化策略，将机组恢复过程划分为多个时步，并采用改进的遗传算法进行求解，但未对负荷恢复进行优化，难以保证机组恢复过程中系统的稳定性。文献［4］建立了单目标的优化模型，将模型离散化为多个“背包”问题，并采用回溯算法逐一求解，但文中优化模型的目标函数仅考虑了机组的发电量，忽略了机组所在节点的重要性，另外文献也未考虑负荷的优化控制及无功电压问题。在负荷恢复方面，文献［5］将机组启动过程中的负荷恢复分为两方面进行优化，即平衡机组出力的负荷恢复和向线路充电时的负荷恢复，但优化中所采用的二分法收敛速度较慢，并不适用于规模较大的系统。

相较于传统电网，微电网的黑启动研究正处于起步阶段。文献［6］通过对微电源及逆变器进行分析，建立了低压微电网的控制模型，并结合多代理技术，提出了有效的恢复策略。文献［7］提出了基于分层多代理技术的微电网黑启动策略，通过对具有黑启动能力的微电源进行预启动和同步运行，逐步实现了微电网系统的恢复，并在一定程度上提升了黑启动的稳定性。

鉴于微电网的黑启动研究尚未深入，本文针对微电网黑启动中的DG恢复阶段提出了DG启动的多目标优化策略，同时兼顾了启动过程中的负荷恢复问题，制定了一套完整有效的DG恢复方案。

1 DG启动的优化模型

DG恢复阶段是负荷恢复阶段的前提和基础，只有在确定DG启动顺序之后才能根据各DG的恢复情况确定应恢复的负荷节点、投入顺序以及投入量值，以达到维持系统功率平衡、电压频率稳定的目的，为此首先需完成DG恢复的优化，进而在优化结果的基础上完成负荷恢复的优化。

为了简化DG恢复过程，本文采用离散时间段的方法，即将连续的DG恢复阶段划分为多个时步，针对每一时步建立DG启动优化模型和负荷恢复模型并求解，最后综合所有时步的最优解按时序进行组合，得到最终的DG恢复方案。本文设定DG恢复阶段的优化总时间为T，被划分为N个时步，时步步长为Δt。为使分析具有普适性，以下将针对第k时步的DG启动和负荷恢复进行优化计算。

1.1 DG启动次序安排的一般原则

DG启动次序的确定是DG恢复阶段需要解决的首要问题，参考传统电网的机组恢复原则［8］，并分析各DG特性对启动的影响程度，提出以下几点原则。

a.优先安排容量大的DG启动。

DG恢复阶段的最终目标是得到尽可能多的系统出力以尽快恢复负荷供电。因此，优先启动容量大的DG能够在短时间内为负荷提供足量的恢复功率。

b.优先安排离重要负荷近的DG启动。

启动重要负荷附近的DG利于缩短向重要负荷供电时的送电路径，减少重要负荷的恢复时间。

c.优先安排带载能力强的DG启动。

带载能力强的DG能够在相同的时间内带动更多的负荷。为此，优先安排启动带载能力强的DG以尽快完成负荷恢复供电，DG的带载能力采用DG在单位时间内所能承载的负荷变化（单位：%/min）表示。

d.优先安排启动时间短的DG启动。

DG启动时间的长短直接关系到系统的恢复速度，启动速度较慢的DG将会给下一时步的DG出力和负荷恢复造成不良影响。

e.优先安排调压、调频能力强的DG启动。

在微电网的黑启动过程中，为了给系统提供参考电压和频率，具有黑启动能力的DG采用V/f控制，而无黑启动能力的DG则采用PQ控制，不同控制方式下的DG会表现出不同的调压、调频能力，V/f控制的DG可以缓冲恢复过程中的扰动，减少电压、频率越限情况的发生。DG的调压、调频能力可分为弱、较弱、一般、较强、强5个等级。

1.2 DG的黑启动能力评估

DG的黑启动能力是指不借助于外部电源的帮助，仅依靠自身启动电源平稳启动，并能在启动后给一定量的负荷提供稳定供电的能力。一般而言，具有黑启动能力的DG应具有以下特性：

a.电压源输出特性；

b.充足的发电容量与备用容量；c.启动迅速；

d.带载能力强；

e.较强的调压、调频能力。

因此，本文采用灰色多属性决策方法［9］，综合考虑DG的容量、启动时间、带载能力以及调压、调频能力，对不同类型的DG进行黑启动能力评估。

灰色多属性决策采用灰色系统理论效果测度的方法，对多个决策组合进行计算得到决策矩阵，进而根据决策矩阵和属性权重评估方案的优劣。

在灰色多属性决策中，决策组合包括事件集、对策集以及局势矩阵。事件集也即属性集，可记作E=｛ei|i=1，2，…，n｝；对策集是所有备选方案的集合，记作 C=｛cj|j=1，2，…，m｝；任一方案 cj在任一属性ei下的评估结果rij称为局势，根据每个方案在每个属性下的评估结果就可建立局势矩阵 R=［rij］n×m。灰色多属性决策过程如下。

a.效果测度。

类似于灰色关联分析，在任一属性ei下的方案评估结果序列｛ri1，ri2，…，rim｝中，各元素与虚拟标准列的相关关系以效果测度ηij表示。ηij的求取方法依属性期望的目标效果而定。

属性期望最大时，采用上限效果测度，即：

属性期望最小时，采用下限效果测度，即：

有特定属性期望时，采用特定中心效果测度，即：

其中，j=1，2，…，m；η′i为属性 ei下的特定评估结果期望。

b.决策矩阵。

以效果测度ηij为基础，对包含n个属性、m个备选方案的决策组合建立决策矩阵H：

c.决策评分。

对每个方案cj在所有属性下进行综合决策，在采用权重交换法［9］确定各属性权重ωHi后，结合决策矩阵对方案评分，综合评分结果如下：

其中，ωHiϵ［0，1］。

根据上述决策过程，对多个DG备选方案进行综合评分，并将各方案按分数从高到低排序，评分最高的即为黑启动能力最强的DG。

1.3 目标函数

在DG恢复阶段，为了尽快给系统提供尽可能多的有功出力，并有利于后续阶段中重要负荷的恢复供电，按照前文中所提的离散时间段的方法，将第k时步优化模型的目标函数设定为：

其中，第1个目标设为在当前时步内启动DG所提供的发电量最大，第2个目标设置为该时步内启动DG附近的负荷重要度之和最大；nG.k为第k时步待启动DG的数目；Δt为时步步长；aGi为第i个DG的启动状态，aGi=1表示DG启动，aGi=0表示DG未启动；Pi（t）为第 i个 DG 在 t时刻的有功出力；Zi为第 i个DG附近负荷重要度；ωZ.l为l级负荷的负荷权重；Zi.l为与第i个DG相连的所有节点负荷中l级负荷所占的比重。

1.4 约束条件

约束条件包括等式约束和不等式约束。等式约束即为潮流方程，包括有功功率和无功功率的平衡方程。不等式约束表述如下：

其中，分别为第i个DG有功出力的下限和上限；分别为第i个DG无功出力的下限和上限；分别为第i个节点上电压所允许的最小值和最大值；nP为系统节点总数；PXi为第i条线路流过的有功功率；为第i条线路上所允许流过的最大有功功率；nL为系统线路总数。

2 DG启动优化模型的求解

2.1 多目标粒子群优化算法概述

粒子群优化PSO（Particle Swarm Optimization）算法最早是受鸟群觅食行为的启发而被提出的，由于其具有收敛速度快、计算量小等优点而被广泛应用于工程领域。针对实际应用中的多目标问题，文献［10］提出了基于外部精英集的多目标粒子群优化（MOPSO）算法，通过 Pareto 支配关系［11］更新并选取粒子最优位置，以指导其他粒子寻优，并采用自适应网格法及轮盘赌选择法改善了Pareto前沿分布的均匀性，标准函数测试表明此算法具有与快速非支配排序遗传算法NSGA-Ⅱ、Pareto存档进化策略PAES等高性能多目标进化算法同等的高效性。

2.2 模型求解步骤

为了最大限度地满足1.1节中所述的DG启动原则，本文结合1.2节中对DG黑启动能力的综合评分，将适应值函数设置如下：

其中，γ1、γ2为自适应惩罚因子［12］；ΔGi为第 i个 DG 的黑启动能力综合评分（以下简称黑启评分）低于该时步黑启评分最低要求的值；γmax1、γmax2为最大惩罚系数；I为当前迭代次数；Imax最大迭代次数；Gkmin（k=1，2，…，N）为第k时步黑启评分最低要求，Gkmin值随k的增加而降低。

本文将各DG黑启评分低于该时步最低要求的值以惩罚函数的形式加入目标函数而形成适应度函数，目的是使黑启评分高于时步最低要求的DG优先启动，即黑启动能力强的DG优先启动，这样文中设定的适应值函数就较为全面地顾及了DG启动的各项原则。

求解该模型的具体步骤如下。

a.参数设置与种群初始化。

以nG维的粒子位置代表该时步nG个待恢复DG的启动状态，启动取1，否则取0。因此在种群初始化时需要随机得到一组二进制编码的粒子位置向量。

b.个体最优存档与外部精英集的形成。

将初始化的粒子位置保存至个体最优存档中，并依据Pareto支配关系将非劣适应值对应的粒子位置加入外部精英集中。

c.粒子速度与位置更新。

粒子的个体最优位置取自个体最优存档，而全局最优位置则运用自适应网格法［13］以及轮盘赌选择法从外部精英集中选取分布稀松区域中的1个粒子位置。结合个体最优位置和全局最优位置更新各粒子速度后，利用二进制粒子群算法中的位置更新公式更新粒子位置。

d.个体最优存档与外部精英集的更新策略。

个体最优存档保持其中成员为该粒子历史非劣适应值所对应的位置。而对于外部精英集，若其规模未达到规定大小，则将非劣粒子位置直接加入；否则根据支配关系判定是否将新粒子位置与精英集中成员交换。

e.迭代终止条件。

如果迭代次数达到了预先设定的最大迭代次数，则计算终止并输出结果，否则返回步骤c重新计算，直至满足迭代终止条件。

2.3 最优解选取

由于最优解集即为外部精英集，外部精英集的规模决定了最优解集的规模，因此求解模型后会得到多个互不支配的DG启动方案，为了根据决策者的预期选择最优启动方案，本文采用直觉模糊数多属性决策方法［14］进行决策分析。

在决策问题中，设 S=｛si|i=1，2，…，m｝为方案集，X=｛xj|j=1，2，…，n｝为属性集，W=｛ωj|j=1，2，…，n｝为与属性对应的权重集，其中ωj为属性xj的权重，并满足 ωjϵ［0，1］。

a.产生直觉模糊决策矩阵。

决策者对方案si关于属性xj进行评估得到直觉模糊数ij=（αij，βij），其中，αij为决策者评估方案si满足属性xj的程度，βij为决策者评估方案si不满足属性xj的程度。综合各直觉模糊数，即可构成直觉模糊决策矩阵

b.确定最优属性权重。

考虑本文中需解决的决策问题，此处采用属性权重信息不完全情况下的偏差最大化方法计算最优权重。构造方案si与其他方案sk关于所有属性xj的总偏差 Bi（ω）：

其中，为加权海明距离。

为求取最优属性权重值，现构造偏差函数：

结合各属性权重不完全信息集合V，得到以下线性规划模型：

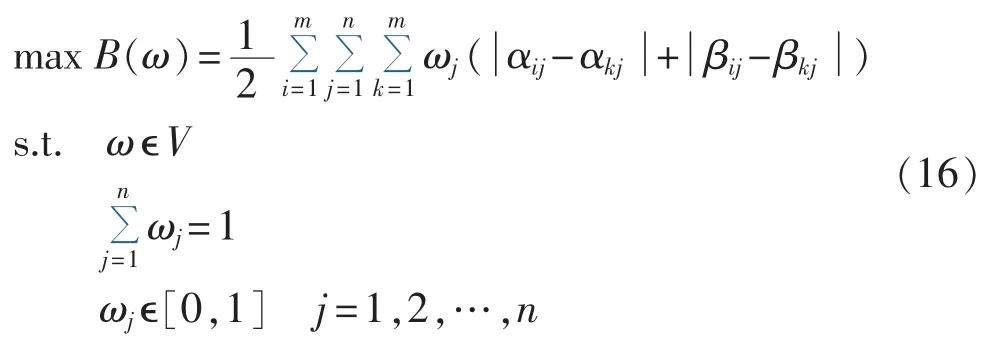
求解此模型即可得到各属性权重的最优值。

c.计算方案综合属性值。

采用直觉模糊加权平均（IFWA）算子计算方案si的综合属性值i：

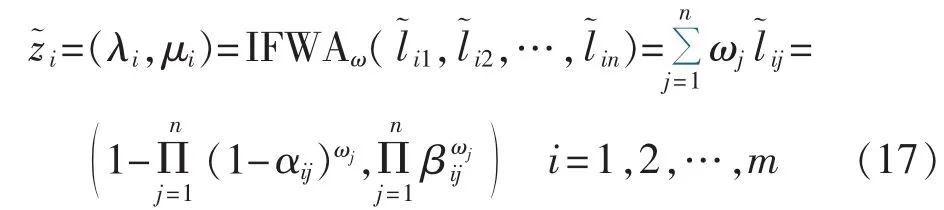
d.综合属性值评分。

对方案 si的综合属性值求取计分函数

若值相同，则进一步计算其精确函数

其中，λi和μi分别为方案si符合和不符合决策者预期的综合隶属度。

最后根据和值的大小对所有方案进行排序，函数值越大的方案越符合决策者预期。

2.4 DG恢复路径优化

DG恢复路径的优化，需要首先给待恢复网络中的每条线路赋予路径权值，然后以节点之间路径权值之和最小为原则，采用最短路径搜索算法为待恢复DG选择最优恢复路径。

为使得最优恢复路径所代表的恢复时间最短，采用文献［15］所述的线路操作时间对线路赋权，根据操作人员经验确定乐观操作时间L、悲观操作时间B以及最可能估计时间K，而线路的实际操作时间则在L和B之间呈贝塔分布，操作时间tCi的期望和方差分别为：

其中，E（tCi）为操作时间 tCi的期望值；σi为操作时间tCi的方差。

结合上述设置的路径权值，采用经典的狄克斯特拉（Dijkstra）算法为各待恢复DG搜索最优恢复路径，所得路径能有效缩短DG的恢复时间，加快黑启动进程。

3 DG启动过程中的负荷恢复优化

3.1 负荷恢复的优化模型

在确定DG启动顺序并搜索到最优恢复路径后，需要进一步考虑DG启动过程中的负荷恢复问题。而第k时步的负荷恢复优化模型是在求解了该时步DG启动优化模型后建立起来的，建模步骤如下。

3.1.1 目标函数

其中，nF.k为第k时步待恢复的负荷节点个数；aLi为负荷i的投入状态，aLi=1表示负荷投入，aLi=0表示负荷未投入；ωLi为负荷i的负荷权重；PLi为负荷i的有功功率。

3.1.2 约束条件

a.单次投入的最大负荷量约束。

对于某个负荷节点，单次投入负荷所引起的系统频率下降幅值不应超过标准的频率偏差限值。本文采用文献［16］中的方法计算第k时步中单次投入的最大负荷量Peach.max.k：

其中，Δf为系统所允许的频率最大下降值，取为负值；nQ.k为第k时步已启动并出力的DG个数；PNj为第j个DG的额定有功出力；frj为第j个DG在该时步负荷率下的频率响应值。

b.最大充电路径权值和约束。

在给负荷送电的过程中，为减少负荷的恢复时间，结合2.4节中的方法，根据系统恢复时间要求设定最大充电路径权值和ωsum.max。

c.时步最大可恢复负荷量约束。

第k时步的最大可恢复负荷量Psum.max.k应取该时步所有启动DG的有功出力增量之和。

d.网络约束。

网络约束包括潮流约束、DG有功/无功出力上下限约束、节点电压上下限约束以及线路功率传输极限约束等。

3.2 模型求解

3.2.1 约束条件的处理

对于约束条件a和b，根据该时步待恢复负荷节点的负荷量及其充电线路的路径权值和，将不满足这2个约束条件的负荷节点剔除，接下来的模型求解中只考虑剩余的负荷节点。

对于约束条件c，将此条件以罚函数的形式加入目标函数中，形成模型求解的适应值函数：

其中，γL为自适应惩罚因子；为最大惩罚系数。

3.2.2 基于二进制粒子群优化算法的模型求解步骤

鉴于所建模型的离散特性，本文采用改进的二进制粒子群优化（MBPSO）算法［17］求解模型，计算步骤如下。

a.参数设置与种群初始化。

类似于DG启动优化模型，以nF维粒子位置代表nF个待恢复负荷节点的投入状态，粒子位置取值为1表示投入，粒子位置取值为0表示未投入，因此粒子位置采用nF位的二进制编码。另外，为获得较好的最优解搜索效果，算法中的惯性权重采用自适应惯性权重。

b.最优位置的初步选取。

将粒子的随机初始位置作为个体最优位置，并以适应值最小为原则选取全局最优位置。

c.粒子速度与位置更新。

根据粒子的最优位置更新粒子速度，然后采用二进制更新公式更新粒子位置。

d.最优位置更新。

利用更新后的粒子位置计算各粒子适应值，然后再次以适应值最小为原则更新粒子的个体最优与全局最优位置。

e.迭代终止条件。

如果全局最优位置对应的适应值达到收敛精度或迭代次数达到最大值，迭代结束，输出结果；否则返回步骤c重新计算，直至满足迭代终止条件。

在得到负荷恢复优化模型的最优解后，综合前文所求得的DG启动优化模型最优解，就可形成一套完整的DG恢复方案，指导DG恢复阶段顺利进行。

4 算例分析

图1为综合文献［18］设计的算例以及IEEE 30节点算例得到的微电网模型，基于MATLAB仿真软件对DG恢复阶段进行了仿真计算，以验证所提方案的有效性。

图1 30节点微电网结构Fig.1 Structure of 30-bus microgrid

如图1所示，此微电网系统包括7个DG、30个负荷节点以及41条线路。各DG的相关参数如表1所示，由于DG2容量大，带载能力强且调压、调频能力强，因此将其作为黑启动微电源之一，并安排在第1时步之前启动并网。本文设置优化总时间T为24 min，时步步长 Δt为 8 min。

参照表1中各DG的容量、启动时间、带载能力以及调压、调频能力值，采用灰色多属性决策方法评估各自的黑启动能力，得到的黑启动能力综合评分如表1所示。

在第1时步中，系统中有6台待启动DG，首先进行DG启动的优化计算。在MOPSO算法中，设置粒子种群数为50，粒子速度和位置维数为6，最大迭代次数为50，惯性权重最大值和最小值分别为0.9、0.4，外部精英集规模设置为3。另外，本文设定1级负荷权重取1，2级负荷权重取0.3，3级负荷权重取0.08。计算得到3组互不支配的DG启动方案，每组方案对应的发电量和负荷重要度之和如表2所示。将发电量和负荷重要度作为方案的2个属性，应用直觉模糊数多属性决策方法从3个方案中选取最优。由于DG恢复初期最主要的目的是尽快给系统提供足够多的有功功率，故根据专家决策建议将发电量的属性权重范围设置为［0.73，0.80］，负荷重要度属性权重范围设置为［0.20，0.27］，计算得到计分函数值如表2最后1列所示，据此选择方案1作为该时步最优DG启动方案。按照选取的DG启动方案，结合路径权值并采用Dijkstra算法，搜索得到了待启动DG的最优恢复路径，应投入的线路为：2-6、6-10、10-21、21-22、6-28、28-27。然后进行此时步的负荷恢复优化，在MBPSO算法中，种群规模设置为30，速度限值设置为［-4，4］，惯性权重的最大、最小值分别设置为0.9、0.4。另外，系统所允许的频率最大下降值Δf设置为-0.2 Hz。优化计算得到该时步可恢复的负荷节点为节点 2、6、10、22、27。最后对该时步整体恢复方案进行潮流校验，未出现潮流越限情况，方案可行。

后续时步恢复方案的优化过程可参照第1时步进行。值得注意的是，在直觉模糊数决策过程中，发电量和负荷重要度的属性权重范围应随时步的推移而作相应的改变。故在考虑专家决策建议的基础上，将第2时步的发电量、负荷重要度的属性权重范围分别设置为［0.41，0.52］、［0.48，0.59］；第 3 时步的发电量、负荷重要度的属性权重范围分别设置为［0.32，0.43］、［0.57，0.68］。最终计算得到的各时步恢复方案如表3所示。

表1 DG的各项参数Table 1 Parameters of DGs

表2 第1时步的DG启动方案Table 2 DG startup scheme for Step1

表3 各时步的DG恢复方案Table 3 DG restoration scheme for all steps

在表3所示的DG恢复方案中，DG22、DG27由于具有较强的黑启动能力，且能在恢复初期快速为系统提供更多的有功出力，因而被优先启动。第2时步中，恢复重要负荷节点以初步形成恢复网架变得更加重要，因此优先恢复节点重要度更大的DG3、DG13。从算例结果可以看出，除去黑启动微电源的启动过程，整个系统的DG恢复在3个时步内完成，达到了黑启动快速性的要求；且方案初步实现了部分枢纽节点以及重要负荷的恢复供电，为后续网架恢复和负荷恢复阶段奠定了基础；最后在潮流检验中，网络中未出现潮流越限的情况，实现了黑启动的稳定性目标。

5 结论

本文针对微电网黑启动的DG恢复阶段制定了DG启动方案及启动过程中的负荷恢复方案。在DG启动的优化过程中，提出了兼顾发电量和负荷重要度的多目标优化模型，MOPSO算法的采用保证了所得最优解集的收敛性和多样性；在负荷恢复的优化过程中，算法所考虑的单次投入负荷量约束及充电路径权值和约束保证了系统频率和节点电压的稳定，计算所得的应恢复负荷节点集合初步构成了系统恢复的主网架，有利于网架恢复阶段顺利进行；最后通过30节点微电网的算例分析，验证了所提方案的可行性。

［1］孟强，牟龙华，许旭锋，等.孤立微电网的黑启动策略［J］.电力自动化设备，2014，34（3）：59-64.MENG Qiang，MU Longhua，XU Xufeng，et al.Research on isolated microgrid black-start［J］.Electric Power Automation Equipment，2014，34（3）：59-64.

［2］刘艳，张凡，顾雪平.大停电后的机组投运风险评估［J］.中国电机工程学报，2013，33（31）：106-113.LIU Yan，ZHANG Fan，GU Xueping.Risk assessment for restoring units following large-scale blackout［J］.Proceedings of the CSEE，2013，33（31）：106-113.

［3］朱冬雪，顾雪平，钟慧荣.电力系统大停电后机组恢复的多目标优化方法［J］. 电网技术，2013，37（3）：814-820.ZHU Dongxue，GU Xueping，ZHONG Huirong.A multi-objective optimization method for post-blackout unit restoration［J］.Power System Technology，2013，37（3）：814-820.

［4］刘强，石立宝，周明，等.电力系统恢复控制的机组优化启动策略［J］. 电力自动化设备，2009，29（4）：1-5.LIU Qiang，SHI Libao，ZHOU Ming，et al.Optimal start-up strategy ofunitsduringpowersystem restoration ［J］.Electric Power Automation Equipment，2009，29（4）：1-5.

［5］瞿寒冰，刘玉田.机组启动过程中的负荷恢复优化［J］.电力系统自动化，2011，35（8）：16-21.QU Hanbing，LIU Yutian.Load restoration optimization during unit start-up stage［J］.Automation of Electric Power Systems，2011，35（8）：16-21.

［6］MOREIRA C L，RESENDE F O，PEAS LOPES J A.Using low voltage microgrids for service restoration［J］.IEEE Transactions on Power Systems，2007，22（1）：395-403.

［7］CAIN，XU X，MITRA J.A hierarchicalmulti-agentcontrol scheme for a black start-capable microgrid［C］∥Power and Energy Society GeneralMeeting，2011 IEEE.San Diego，USA：IEEE，2011：1-7.

［8］谢夏慧，汪沨，黎灿兵.基于模糊AHP的DG启动顺序的优化［J］.电源技术，2014，38（7）：1367-1369.XIE Xiahui，WANG Feng，LI Canbing.Optimization of DG startup sequence based on fuzzy AHP［J］.Power Technology，2014，38（7）：1367-1369.

［9］简祯富.决策分析与管理［M］.北京：清华大学出版社，2007：157-359.

［10］COELLO C A C，PULIDO G T，LECHUGA M S.Handling multiple objectives with particle swarm optimization［J］.IEEE Transactions on Evolutionary Computation，2004，8（3）：256-279.

［11］栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划［J］. 电力自动化设备，2014，34（1）：6-13.LI Ran，MA Huizhuo，ZHU Jinyao，et al.Multi-objective optimization for DG integration into distribution system［J］.Electric Power Automation Equipment，2014，34（1）：6-13.

［12］姜文，程叶霞，严正，等.考虑可靠性约束的含风电场电力系统动态经济调度［J］. 电力自动化设备，2013，33（7）：27-33.JIANG Wen，CHENG Yexia，YAN Zheng，etal.Reliabilityconstrained dynamic economic dispatch of power system with wind farms［J］.Electric Power Automation Equipment，2013，33（7）：27-33.

［13］YUAN Q，ZHENG J，LI M，et al.A multi-objective evolutionary based on hybrid adaptive grid algorithm［C］∥2011 IEEE Seventh International Conference on Natural Computation（ICNC）.Shanghai，China：IEEE，2011：1237-1241.

［14］卫贵武.对方案有偏好的区间直觉模糊多属性决策方法［J］.系统工程与电子技术，2009，31（1）：116-120.WEIGuiwu.Method forinterval-valued intuitionistic fuzzy multiple attribute decision making with preference information on alternatives［J］.Systems Engineering and Electronics，2009，31（1）：116-120.

［15］曾顺奇，文福拴，薛禹胜，等.计及操作时间不确定性的电力系统网架重构策略优化［J］. 电力系统自动化，2012，35（23）：16-21.ZENG Shunqi，WEN Fushuan，XUE Yusheng，et al.Optimization of network reconfiguration strategy for power systems considering operating time uncertainty［J］.Automation of Electric Power Systems，2012，35（23）：16-21.

［16］ADIBI M M，BORKOSKI J N，KAFKA R J，et al.Frequency response of prime movers during restoration ［J］.IEEE Transactions on Power Systems，1999，14（2）：751-756.

［17］关龙，刘志刚，何士玉，等.离散二进制粒子群算法在基于模型配电网故障诊断中的应用［J］. 电力自动化设备，2013，33（9）：89-93.GUAN Long，LIU Zhigang，HE Shiyu，etal.Application of BPSO algorithm in model-based fault diagnosis of distribution network［J］.Electric Power Automation Equipment，2013，33（9）：89-93.

［18］彭克，王成山，李琰，等.典型中低压微电网算例系统设计［J］.电力系统自动化，2011，35（18）：31-35.PENG Ke，WANG Chengshan，LIYan，etal.Design ofa typical medium-low voltage microgrid network［J］.Automation of Electric Power Systems，2011，35（18）：31-35.