新型混合SVC模型及其基于人工免疫算法的控制策略
陈赛赛,李可军,王卓迪,闫文宁
(山东大学 电气工程学院,山东 济南 250061)
0 引言
随着经济和社会的发展,负荷结构日趋复杂,用户对电能质量要求进一步提高,传统的静止无功补偿器(SVC)逐渐暴露出响应速度慢、谐波含量高等缺点,严重影响其补偿效果[1]。而性能较好的静止无功发生器(SVG),尤其是大容量SVG,成本过高,一次性投资巨大,普通用户难以承受[2]。因此,研究一种既有SVC的成本优势又有SVG的性能优势的混合型无功补偿装置模型适应市场需求,具有较高的经济效益和现实意义。
针对该类混合型无功补偿装置,国内学者已经做了一些初步的研究[3-4],但仅限于电容器组与SVG的联合运行方面的研究,应用面过于狭窄且控制策略简单、适用性较差。
文献[3]为改善变电站动态无功补偿的效果,研究了人工投切电容器配合STATCOM联合运行的控制策略,并分析了其性能。然而,电能质量问题往往是瞬时性的,人工投切电容器难以做到实时调整,在实际应用中将严重制约其整体性能。
相比文献[3],文献[4]中电容器组部分采用了晶闸管投切电容器(TSC),解决了实时配合的问题,有较好的效果。但文献[4]的研究仅仅是针对异步电动机,应用面过于狭窄,并且在控制策略层面并未将其推广至负荷构成更加复杂的实际电网。此外,文献[4]未采用晶闸管控制电抗器(TCR),仅仅采用TSC配合SVG,故在输出无功变化的情况下,感性输出部分完全依赖SVG,这样会对SVG的容量要求更高,从而造成较高的制造成本,实际的经济效益将会受到制约。
基于智能算法的动态PI控制策略相关研究也较多[5],该类研究在硬件结构上都是基于传统的PI控制结构,在智能算法上多采用模糊控制等早期智能算法,应用面狭窄,在内部结构相对复杂的情况下并没有就模块间的协调问题作深入研究。
鉴于此,本文提出的混合型无功补偿器采用的是FC+TCR+SVG的模式,即SVC+SVG。TCR的引入将减轻SVG的负担,可以进一步减小SVG的容量。在结构上,将小容量SVG以模块的形式嵌入大容量SVC内部,同时引入了具有良好动态性能的改进型PI控制器结构,并针对模型的特点,设计了基于人工免疫算法的控制策略,实时整定控制器参数,以满足系统对各部分动态性能的要求。最后,给出了各模块间的协调控制策略。基于PSCAD的仿真验证了该控制策略的有效性和模型的经济性。
1 新型SVC电路结构分析
SVC模块电路由TCR与固定电容器组(FC)构成,其控制电路采用复合控制方法,即采用前馈与反馈相结合的控制策略[6-8]。SVG模块电路采用单桥路结构,其控制方法亦采用复合控制方法。
出于使用、维护、升级的灵活性以及可作为原SVC项目的改造手段的考虑,本模型采用模块化的设计思想,即装置内部在布局上需保持模块间相互独立。若将SVC(FC+TCR)看作整体,结合电源侧与负载侧的相对位置,有2种可能的布局方式:结构1与结构2。
1.1 模块布局结构1
SVC模块与SVG模块相互独立,SVC模块靠近电源侧,SVG模块靠近负载侧。电路结构如图1所示。
可见,该结构下,SVC的控制环与SVG的控制环互相独立,没有形成闭环,因此两模块的控制信号之间不会相互干扰,同时,SVC与SVG的控制系统均处于由电容C和系统阻抗Zs构成的谐振回路之外,故控制系统可靠性较高。
但这种结构下,SVG处于负载侧,仅能补偿负载的谐波,而TCR处于电源侧,工作时产生的谐波无法被SVG补偿,会对系统侧电网造成污染。

图1 结构1的拓扑结构Fig.1 Topology of Structure 1
1.2 模块布局结构2
SVC模块与SVG模块相互独立,SVC模块靠近负载侧,SVG模块靠近电源侧。电路结构如图2所示。

图2 结构2的拓扑结构Fig.2 Topology of Structure 2
可见,该结构下,与结构1一样,SVC的控制环与SVG的控制环互相独立,没有形成闭环,因此两模块不会相互干扰,工作时不会产生稳定性问题,同时TCR处于负载侧,其产生的谐波由SVG补偿,不会对系统侧电网产生污染。但此时,由电容C和系统阻抗Zs构成的谐振回路包含了SVC的控制系统,谐振会严重威胁SVC控制系统的正常运行,故该系统可靠性较差。
1.3 可行的结构
通过以上2种结构的分析可以发现,保持SVC模块与SVG模块相互独立无法很好地同时满足系统对性能与稳定性的要求。
针对这个实际问题,本文的解决方案是:将SVC模块进一步分解成TCR模块与FC模块。结合对TCR模块、FC模块和SVG模块各部分的特点,提出一种兼顾性能与稳定性的可行的结构。
TCR模块、FC模块和SVG模块相互独立,TCR模块靠近负载侧,FC模块靠近电源侧,SVG模块位于中间。电路结构如图3所示。

图3 可行的拓扑结构Fig.3 Feasible topology
将TCR靠近负载侧,使其产生的谐波被SVG补偿;FC靠近电源侧,使电容C与电网阻抗Zs构成的谐振回路不影响SVC与SVG的控制环,增强系统的稳定性。
但此时,SVC的控制环与SVG的控制环互相形成闭环,为避免控制环之间的相互干扰,同时为了提高两模块合作的效率,必须设计相应的协调控制策略,以提高系统的可靠性。
2 基于免疫算法的改进型PI控制器
针对SVC控制系统与SVG控制系统中均采用的PI调节器,提出了基于人工免疫算法的改进型PI环节,通过免疫算法实时动态调整PI控制参数,以达到最佳的响应性能及实现模块间的协同配合。
为提高该算法的适应性以及满足客户的差异化需求,本文引入支持向量机算法,根据不同环境下对性能的不同要求,优化免疫函数,增强该算法的适应性。
2.1 采用改进型PI控制环节
对于传统的PI环节(如图4所示,图中标记为“+”的信号,表示直接输入系统;标记为“-”的信号,表示取其负值后输入系统,后同),当通过调整参数提高系统的响应速度时,将会引起较大的超调量;当系统超调量为零,系统响应速度则过于缓慢。响应速度与系统超调量之间的矛盾是由系统结构造成的,只能从调整系统结构的角度加以解决[9]。
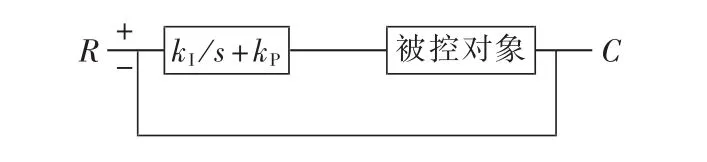
图4 传统PI环节结构Fig.4 Structure of traditional PI controller
本文将传统的PI环节改接成如图5所示的结构,对于比例环节kP,只与反馈信号C相乘,而不是与误差信号R-C相乘,这样,理论上可以实现无超调阶跃响应,同时,这种改进型调节器的比例增益和积分增益的变化并不影响负荷的调整。因此,改进型PI环节的综合动态性能更好。

图5 改进型PI环节结构Fig.5 Structure of improved PI controller
假设被控对象为纯积分环节,其传递函数为:

则传统PI环节的闭环传递函数为:

改进型PI环节的闭环传递函数为:
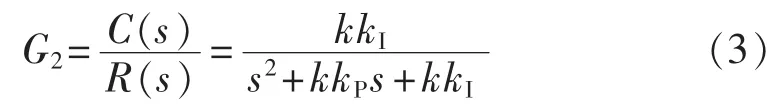
其阶跃响应对比曲线见图6(取k=kI=kP=1)。

图6 传统PI环节与改进型PI环节的阶跃响应对比曲线Fig.6 Comparison of step response curve between traditional and improved PI controller
可见,从超调量来看,相比传统PI环节的约30%的超调量,改进型PI环节的超调量非常小,几乎为零;从响应速度来看,改进型PI环节仅用了3 ms稳定于设定值,而传统型需要大约12 ms,改进型的响应速度是传统型的4倍。因此,改进型PI环节无论是响应速度还是超调量,均优于传统型PI环节,对于需要兼顾响应速度与超调量的新型SVC系统,这种改进型PI调节器是合适的选择。
2.2 PI参数的在线动态优化
传统PI控制器参数kP、kI在整个调节过程中始终保持不变,由于PI控制本质上是一种线性控制,其参数的整定值是局部最优值,而非全局最优值。这极大地限制了PI控制器性能的发挥,很难满足特殊情况下对系统响应速度的要求[10]。
针对这一问题,本文将改进型PI调节器和人工免疫算法相结合,利用免疫控制策略,根据不同的偏差、偏差变化率对PI控制器的参数kP、kI进行实时调整,用实时动态优化的PI参数去适应SVC控制的全过程,以提高其动态性能。在系统响应的初期,可以通过增大kP且减小kI来提高其响应速度;在系统响应的末期,系统目标值比较接近设定值时,可以通过减小kP且增大kI来减小其超调量。动态PI控制器兼顾了响应速度与超调量,使其响应性能获得全局最优。
2.3 免疫算法与控制器建模
免疫是生物体的一种生理反应,是一个极其复杂的自适应系统。人体免疫原理如图7所示[11-12],其中实线代表正向作用(在该作用下数量增加),虚线代表反向作用(在该作用下数量降低)。
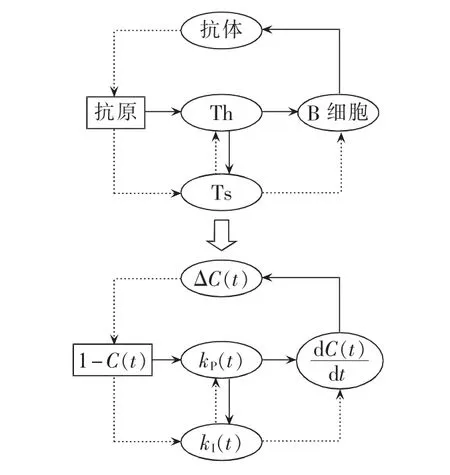
图7 人工免疫算法简化原理图Fig.7 Simplified schematic diagram of artificial immune algorithm
类比PI控制系统与生物的免疫响应过程,系统输出瞬时值与设定值之间的差值相当于抗原,比例系数kP相当于辅助细胞Th的数量,积分常数kI相当于抑制细胞Ts的数量。在系统控制的初期,抗原数量较大(输出瞬时值较小,系统输出瞬时值与设定值之间的差值较大),刺激产生较多的辅助细胞Th(增大kP,提高响应速度)和较少的抑制细胞Ts(减小kI),在系统控制的末期,抗原数量较小(输出瞬时值比较接近设定值),刺激产生较多的抑制细胞Ts(增大kI,提高系统稳态精度,降低超调量)减少辅助细胞 Th(减小 kP)。
假设t时刻系统的控制瞬时输出值为C(t),动态 PI参数瞬时值为 kP(t)、kI(t),则在 t+Δt时刻有:

其中,fTh(·)为辅助细胞函数,其选取反映了系统对响应速度的要求;fTs(·)为抑制细胞函数,其选取反映了系统对稳态精度与超调量的要求;fB(·)为B细胞函数,其选取反映了系统对整体性能的调节能力。
由式(4)可求得每个时刻动态PI参数瞬时值kP(t)、kI(t),从而实现对 PI控制器的全局动态优化,其流程图如图8所示。

图8 基于免疫算法的改进型PI控制流程Fig.8 Flowchart of improved PI control based on immune algorithm
2.4 支持向量机优化免疫函数
为了不失一般性,将不同的函数(fTh(·)、fTs(·)、fB(·))统称为免疫函数 f(x),根据不同要求(如响应速度、稳态精度、超调量和整体性能等),产生支持向量机优化算法所需的函数预期响应的样本集{(x1,y1),(x2,y2),…,(xl,yl)},将系统的 PI控制器参数kP、kI以及 1-C(t)共 3 个特征量作为支持向量机模型的输入量 xi=[kP,kI,1-C(t)],免疫函数对应的取值f(xi)作为模型的输出量,yi为样本集内预期输出的实际值,l为样本数。样本x通过非线性空间映射到高维空间,同时,依据结构风险最小定理[13-14],构造回归函数:

通过支持向量机训练可求得免疫函数f(x)的支持向量机拟合函数为(结构如图9所示):

其中,αi、α*i为引入的非负的 Lagrange 乘子;K(xi,x)为核函数,核函数采用径向基核函数[15-16],如式(7)所示。


图9 支持向量机优化结构图Fig.9 Optimal structure of support vector machine
3 基于免疫PI控制器的SVC模块与SVG模块协调控制
SVC模块与SVG模块的控制器之间差异较大,主要是其动态性能指标不同[17]。SVG响应迅速,其开环响应时间常数为1/4个周期,而SVC为2个周期,故两者控制器之间易发生相互干扰,影响整体性能的发挥。
此外,两模块间动作的先后顺序也较为关键。当无功缺额较大时,由于SVG响应时间常数非常小,其会率先动作,立刻进入极限的输出状态并保持极限运行,导致其没有充足的无功储备,严重影响后期滤波效果。
为了解决上述问题,本文提出了如图10所示的模块间协调控制方案,并且引入了基于人工免疫算法的改进型动态PI控制器,以保证系统跟踪电压波动、抑制闪变和滤波的性能要求,从而提高各模块的响应速度以及模块间的协调能力。

图10 模块间协调控制流程图Fig.10 Flowchart of coordinative control among modules
3.1 SVG模块控制策略
当电压缺额较大,超出SVG模块最大补偿能力时,SVG模块立即进入闭锁状态,防止其率先动作,不仅无法完成补偿要求,还会影响SVC模块的工作。待SVC模块完成初步粗补偿以后,再开始运行,完成最后的微补偿与消除谐波。
当电压缺额较小时,闭锁SVC模块,由SVG模块单模块运行,完成无功补偿与消除谐波。
3.2 SVC模块控制策略
当电压缺额较大,超出SVG模块最大补偿能力时,SVC模块立即动作,同时,改进型免疫PI控制器动态调整SVC模块的PI控制器参数,使其以最快的响应速度完成粗补偿,并向协调控制器发出粗补偿已完成的信号。
当电压缺额较小时,SVC模块立即闭锁,由SVG模块单模块运行,完成无功补偿与消除谐波。
4 仿真验证
为验证本文所提出的新型SVC控制策略的有效性和经济性,搭建了基于PSCAD的仿真系统,分别对传统的SVC和本文所提出的新型混合SVC进行仿真对比。同时,通过对比不同容量SVG接入后的补偿效果,确定合适的SVG与SVC模块容量比。该系统主电路如图11所示。

图11 仿真系统结构图Fig.11 Structure of simulation system
系统仿真参数如下:系统电压380V,频率50Hz;SVG模块与SVC模块容量比为1∶4;SVG模块PI控制器初始参数kP=3、kI=90;SVC模块PI控制器初始参数 kP=0.5、kI=60。
为了验证新型混合SVC的性能,通过大电感的投切来模拟负载侧电压的跌落现象。
4.1 动态性能对比
在t=1.5 s时,负载侧突然投入大电感,在0.75 s后再切除。
4.1.1 电压响应对比
传统SVC响应曲线与新型SVC的响应曲线对比图如图12所示(图中电压响应为标幺值)。
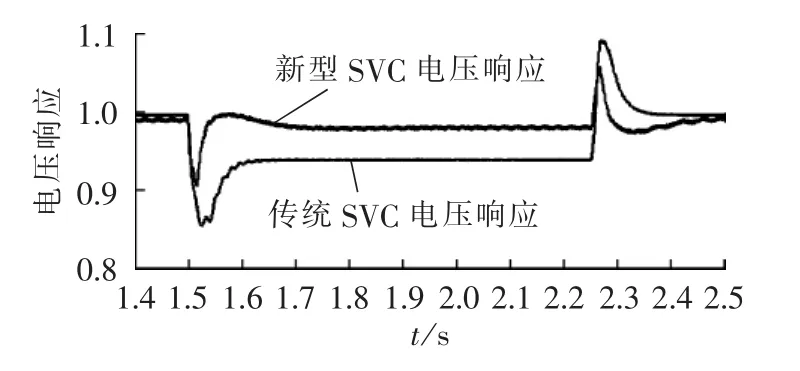
图12 电压响应仿真对比图Fig.12 Comparison of voltage response
从图中可以看出,新型SVC经过3 ms后电压稳定于0.98 p.u.,而传统SVC经过13 ms后稳定于0.93p.u.。可见,新型SVC调节时间更短且补偿效果更好。
4.1.2 功率因数对比
新型SVC与传统SVC的功率因数的变化如图13所示。
从图中可以看出,当大电感投入时,负载侧功率因数迅速下降,相比传统SVC(功率因数跌至0.85以下时才开始动作,最后稳定于0.92),新型SVC的响应速度更快,在功率因数跌至0.9时迅速动作,并很快完成补偿,稳定于0.98左右。由此可见新型SVC在功率因数补偿方面,响应速度更快,补偿效果更好。

图13 功率因数仿真对比图Fig.13 Comparison of simulative power factor
4.2 谐波含量对比
根据仿真结果(以A相为例)分析计算了在平衡负载与不平衡负载下的负载侧谐波含量,如表1、2所示。

表1 传统SVC的谐波含量Table 1 Harmonic contents of traditional SVC

表2 新型SVC的谐波含量Table 2 Harmonic contents of novel SVC
4.2.1 平衡负载
在平衡负载下(如图14所示),负载处5次谐波为主要谐波,含量较大(高达2.85%)。新型SVC补偿后,其5次谐波含量下降至0.54%,其他各次谐波也有不同程度的抑制,滤波效果明显。

图14 平衡负载下谐波含量对比图Fig.14 Comparison of harmonic contents for balanced load
4.2.2 不平衡负载
在不平衡负载下(如图15所示),原负载处3次谐波为主要谐波,含量较大(高达8.21%)。新型SVC补偿后,其3次谐波含量下降至1.51%,滤波效果明显。同时,其他各次谐波也有不同程度的抑制。可见,新型SVC对谐波有较好的抑制作用。
4.3 SVG配置容量优化与成本分析
一般而言,当容量较小时,同容量SVG的成本是SVC的2~3倍;当容量较大时,同容量SVG的成本是SVC的5倍左右。无论对用户还是厂家,成本都是他们最关心的问题之一,本文有必要就性能与成本的关系以及SVG配置容量的优化问题进行仿真,以得出可靠的结论。
基于上述仿真模型,分别设置SVG模块的相对容量(SVG容量占 SVC容量的百分比)为 0、5%、10%、15%、20%、25%、30%、35%,统计其响应速度与各次谐波含量分别如图16、图17所示。

图15 不平衡负载下谐波含量对比图Fig.15 Comparison of harmonic contents for unbalanced load
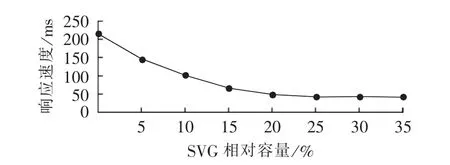
图16 系统响应速度随SVG相对容量变化曲线Fig.16 Curve of system response vs.SVG relative capacity
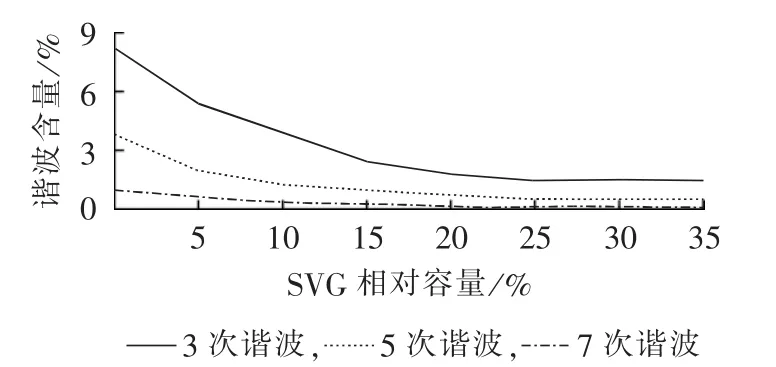
图17 各次谐波含量随SVG相对容量变化曲线Fig.17 Curve of harmonic content vs.SVG relative capacity for different orders
在初期,相对容量较小,随着SVG相对容量的增加,系统响应速度和谐波含量等性能的改善明显;在后期,尤其是相对容量大于25%以后,响应速度和谐波含量曲线趋于“饱和”,性能趋于稳定,但此时,成本却随着SVG相对容量的增大而继续增加。可见,混合型无功补偿器SVG模块相对容量的选取十分关键。
在本仿真算例中,25%是一个相对比较合适、性价比较高的SVG相对容量取值。若取同容量SVG价格为SVC的3倍,则SVG相对容量为25%的混合型无功补偿器的成本相比同容量SVG节省了53.3%,可见,SVG相对容量为25%的混合型无功补偿器既保证了性能的要求,又最大限度地控制了成本。
5 结论
本文结合SVC与SVG在成本和性能方面的特点,提出了一种性价比很高的混合型无功补偿器,并对其内部电路布局合理性以及在运行过程中不同模块控制系统间的协调问题进行分析,提出了基于人工免疫算法的改进型PI控制策略,显著改善了系统的性能。
仿真结果表明,新型混合SVC相比传统SVC响应速度更快、补偿效果更好,且对谐波有较好的抑制作用,性能媲美SVG。同时,混合型无功补偿器SVG模块相对容量的选取十分关键。配置合适相对容量的新型混合SVC(本算例为25%)在不损失性能的前提下,具有显著的经济效益(本算例节省成本53.3%)。
综上所述,本文研究的新型混合SVC模型及其控制策略,在达到同容量SVG相同性能要求的前提下可节省约50%以上的投资,是对国内现有SVC装置进行改造的可行方案之一。
参考文献:
[1]蒋玮,陈武,胡仁杰.基于超级电容器储能的微网统一电能质量调节器[J].电力自动化设备,2014,34(1):85-90.JIANG Wei,CHEN Wu,HU Renjie.United power quality conditioner based on supercapacitor for microgird [J].Electric Power Automation Equipment,2014,34(1):85-90.
[2]何圣仲,许建平,周国华,等.谷值V2控制Boost变换器原理及稳定性分析[J].电力自动化设备,2014,34(7):65-70.HE Shengzhong,XU Jianping,ZHOU Guohua,etal.Principle and stability analysis of valley V2controlled Boost converter[J].Electric Power Automation Equipment,2014,34(7):65-70.
[3]朱永强,崔文进,胡东辰,等.50 Mvar静止补偿器接入系统运行策略仿真研究[J].电力系统自动化,2004,28(21):77-80.ZHU Yongqiang,CUIWenjin,HU Dongchen,etal.Simulation study on the running strategy of the 50 Mvar STATCOM[J].Automation of Electric Power Systems,2004,28(21):77-80.
[4]胡国文,於锋,王威.STATCOM与固定电容组合的高压异步电动机动态无功补偿节能技术[J].电力自动化设备,2011,31(3):75-78.HU Guowen,YU Feng,WANG Wei.Energy-saving technology of dynamic reactive power compensation based on STATCOM and fixed capacitorforHV induction motor [J].Electric Power Automation Equipment,2011,31(3):75-78.
[5]李琼林,刘会金,孙建军,等.基于模糊逻辑的参数自整定PI控制在有源滤波器中的应用[J].电力自动化设备,2005,25(10):17-21.LIQionglin,LIU Huijin,SUN Jianjun,etal.Fuzzy-PIcontrol used in APF[J].Electric Power Automation Equipment,2005,25(10):17-21.
[6]付俊,赵军,乔治·迪米罗夫斯基.静态无功补偿器鲁棒控制的一种新自适应逆推方法[J].中国电机工程学报,2006,26(10):7-12.FU Jun,ZHAO Jun,DIMIROVSK G M.Robust control of SVC:a new adaptive back stepping method [J].Proceedingsofthe CSEE,2006,26(10):7-12.
[7]丁青青,王赞基.TCR-TSC型SVC的非仿射非线性控制器设计[J].电力系统自动化,2002,26(14):12-19.DING Qingqing,WANG Zanji.A new design of TCR-TSC SVC controller based on non-affined nonlinear model[J].Automation of Electric Power Systems,2002,26(14):12-19.
[8]牛伟,房大中.基于GATS混合算法的PSS与SVC控制器参数设计[J].电力系统及其自动化学报,2006,18(1):43-48.NIU Wei,FANG Dazhong.Coordination design of PSS and SVC damping controller using GATS hybrid algorithm[J].Proceedings of the CSU-EPSA,2006,18(1):43-48.
[9]杨火荣.快速响应和无超调的改进型PI调节器[J].工业仪表与自动化装置,1979,2(1):50-53.YANG Huorong.Improved quick response PI without overshoot[J].Industrial Instrumentation&Automation,1979,2(1):50-53.
[10]曾果,李兴源,段毅.基于内模控制理论的HVDC IMC-PID控制器设计[J].电力自动化设备,2014,34(4):162-167.ZENG Guo,LIXingyuan,DUAN Yi.Design ofIMC-PID controller based on internal model control theory for HVDC controlsystem [J].Electric Power Automation Equipment,2014,34(4):162-167.
[11]HUNT J E,COOKE D E.An adaptive,distributed learning system based on the immune system[C]//1995 IEEE International Conference on Systems,Man and Cybernetics.Vancouver,Canada:[s.n.],1995:2494-2499.
[12]DING Y,REN L.Fuzzy self-tuning immune feedback controller for tissue hyperthermia[C]//The Ninth IEEE International Conference on Fuzzy Systems.San Antonio,USA:[s.n.],2000:534-538.
[13]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.ZHANG Xuegong.Introduction to statistical learning theory and support vector machines[J].Acta Automatica Sinica,2000,26(1):32-42.
[14]KEERTHI S S,LIN C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation,2003,15(7):1667-1689.
[15]徐咏梅,柳桂国,柳贺.高斯径向基核函数参数的GA优化方法[J].电力自动化设备,2008,28(6):52-55.XU Yongmei,LIU Guiguo,LIU He.GA based parameter optimization ofGauss kernel function [J].Electric Power Automation Equipment,2008,28(6):52-55.
[16]何旭,姜宪国,张沛超,等.基于SVM的小样本条件下继电保护可靠性参数估计[J].电网技术,2015,39(5):1432-1437.HE Xu,JIANG Xianguo,ZHANG Peichao,et al.SVM based parameter estimation of relay protection reliability with small samples[J].Power System Technology,2015,39(5):1432-1437.
[17]杨振宇,许胜,许杏桃.高压大容量D-STATCOM主电路的比较与分析[J].电力自动化设备,2011,31(6):50-55.YANG Zhenyu,XU Sheng,XU Xingtao.Comparison and analysis ofhigh-voltage large-capacityD-STATCOM main circuit[J].Electric Power Automation Equipment,2011,31(6):50-55.

