变压器油中溶解气体浓度的区间预测

林湘宁 ，黄 京 ，熊卫红 ，翁汉琍 ，朱黎明 ，张 贞 ，谢志成

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.华中科技大学 电气与电子工程学院，湖北 武汉 430074；3.国家电网公司华中分部，湖北 武汉 430077；4.华能北京热电有限责任公司，北京 100023）

0 引言

通过变压器油中溶解气体浓度（每升绝缘油中溶解的气体体积）分析可以及时发现变压器中的一些潜伏性绝缘故障和缺陷，进行精确的变压器油中溶解气体浓度发展趋势预测，能够为变压器绝缘状态评估提供重要依据［1-2］。根据油中溶解气体浓度的变化趋势，可以追踪变压器的运行状态，进一步判断设备内部是否存在异常，推断故障类型，及时发现变压器内部存在的早期故障；若变压器将要发生故障，则能够提前安排检修计划，从而确保了电力系统的可靠稳定运行。

已有的变压器油中溶解气体浓度的预测方法［3-6］主要有径向基神经网络（RBFNN）、最小二乘支持向量机（LSSVM）、灰色理论（GM）及组合预测等。RBFNN具有唯一最佳逼近的特性，且无局部极小值；LSSVM能很好地解决小样本、非线性和局部极小值等问题；GM可以通过少量的、不完全的信息揭示事物的发展规律。但考虑到变压器油中溶解气体浓度可能受到其他因素的影响，仅使用待预测状态量的历史数据建立单一预测模型进行预测时，因单一预测模型本身有其局限性，使得预测精度有限且稳定性较低。也有研究者将多种单一方法进行组合，但组合预测模型的权重若基于专家经验［7-8］会过于主观，或者出现权重为负［9］的情况。此外，变压器油中溶解气体浓度可能受到随机性因素的影响，导致气体浓度产生波动，因此有必要对气体浓度构造预测区间以准确捕捉气体的波动范围。而传统区间预测［10-12］方法需要预测模型的误差样本服从正态分布，但若假设不成立则会导致构造的预测区间可信度不高，无法给状态检修决策者提供可靠的数据。

针对以上问题，本文首先应用关联度分析，将与待预测状态量关联度较高的影响因素引入预测模型的训练样本中以提高模型的预测精度。针对单一预测方法采用固定参数而不涉及参数自适应，引起局部最优，导致无法获得全局最优解的不足，结合RBFNN、LSSVM和GM的优势，建立了组合预测模型。权重的分配是实现组合预测的关键，为使组合预测的权重客观且更科学，采用熵权法［13-14］分配各单一模型的权重，依据信息熵计算出各单一模型的熵权，然后修正各模型的权重，从而得出更为客观的权重值。为了更准确地捕捉气体浓度的变化范围，本文提出基于比例系数法和粒子群优化算法的区间预测方法，用于构造一定置信水平下油中溶解气体浓度的预测区间，有效量化了气体浓度的波动范围，且无需预测模型的误差样本服从正态分布。

1 构造区间预测模型

1.1 数据样本关联度分析

关联度是基于灰色理论［15］提出的一种分析系统中各因素关联程度的方法，其根据曲线间的相似度来鉴别各因素的关联程度，曲线的几何形状越接近，即变化趋势越接近，各因素的关联程度也就越高。

设参考向量为x0，被比较向量为xi，且：

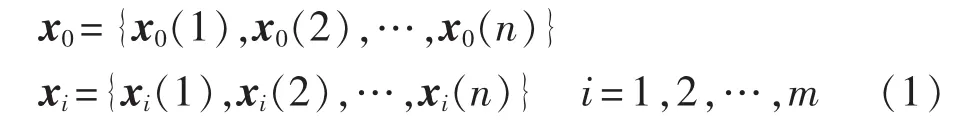
则向量 xi与第 k（k＝1，2，…，n）点的关联系数为：

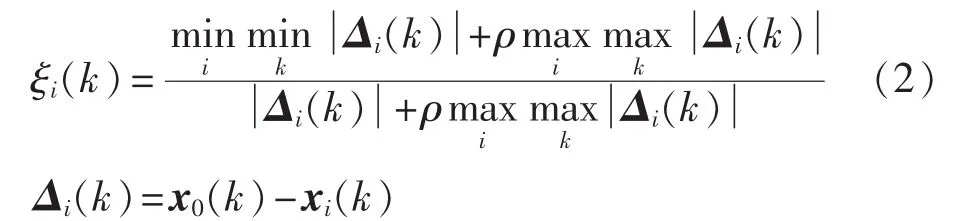
其中，Δi（k）为 x0（k）与 xi（k）之间的绝对误差；和分别为两级最小、最大差；ρ为分辨系数，一般取0.5。

由式（2）可推得xi与x0的关联程度ri为：

1.2 熵权法确定组合预测权重

熵权法综合了各预测模型的重要性和指标提供的信息量，可更客观地确定各模型的最终权重［8，15］。某个预测模型的信息熵越小，表示该模型的变异程度越大，所提供的信息量越多，即在整个预测过程中的作用越大，其权重也越大；反之则越小。

本文提出的组合预测模型使用多种评价指标来评判各单一预测方法的预测精度。第j个评价指标的重要性熵值 e（dj）为：

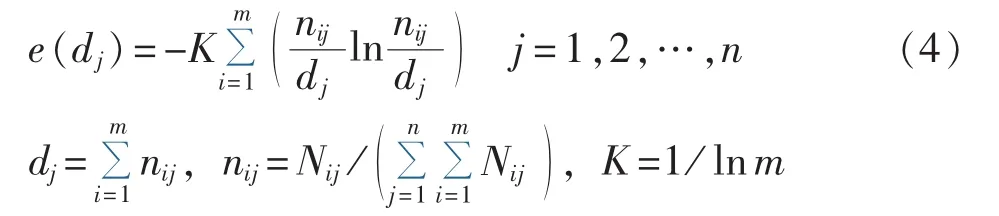
其中，Nij为各评价指标参数值相对于各评价指标的接近程度。

信息熵e（dj）可衡量第j个评价指标信息的有效程度，e（dj）越小则第j个评价指标的有效程度越高。第j个评价指标的信息效用程度hj=1-e（dj）。

熵值法实质上是利用该评价指标信息的效用价值系数来计算各评价指标的客观权重，效用价值系数越高，指标对评价结果的重要性就越大。第j个评价指标的客观权重值θj为：

则第i种预测方法的权重ωi为：

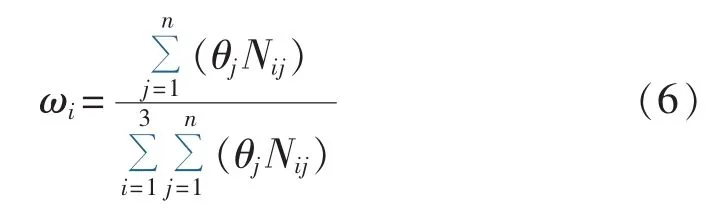
1.3 预测区间的评价指标

对油中溶解气体浓度未来变化趋势的点预测无法准确捕捉到由不确定因素引起的油中溶解气体浓度的波动。准确地量化油中溶解气体浓度的变化范围能够为状态检修决策者提供可靠的参考以便制定更合理的检修计划。因此构造一定置信水平［16］下油中溶解气体浓度的预测区间非常必要。

本文所提的区间预测方法主要是应用比例系数法构造预测区间的上界和下界，然后采用粒子群优化算法对预测区间各评价指标寻优以得到最优的比例系数和，从而构造油中溶解气体浓度的预测区间。预测区间的上界和下界如式（7）所示。

其中，UT和LT分别为未来T时刻预测区间的上界和下界；yT为未来T时刻的组合预测值。

为了更好地评价预测区间的质量，将引入以下评价指标［17-18］来量化预测区间的有效性。

a.预测区间覆盖概率（PICP）。

覆盖概率，也称为置信水平，其决定了预测区间的有效性。PICP表示目标值将处于上界与下界之间的概率，PICP越高，意味着更多的目标值被预测区间覆盖。PICP的定义如下：

其中，t为要预测的时间点数；为实测值。

b.预测区间归一化均方根宽度（PINRW）。

预测区间的质量一般由PICP进行评估，如果目标值都在预测区间内，则相应的PICP会达到100%覆盖。实际上，预测区间太宽是没有意义的，因为它们不能表示有关目标值变化的信息，因此还需要考虑预测区间的宽度。预测区间的宽度决定了它们的信息量，过宽的预测区间只能表达很少的信息并且不能被决策者所用。因此定义了一个可以对宽度进行定量测量的评价指标PINRW：

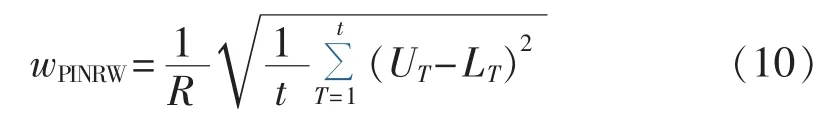
其中，R为目标值的范围，使用参数R的目的是标准化预测区间平均宽度的比例。

c.基于覆盖宽度的准则（CWC）。

PICP和PINRW仅能分别对预测区间的一个方面进行评估，且这2个指标分别为增益型和损失型指标，因此考虑采用一个综合评价指标全面评估预测区间的质量，定义为：

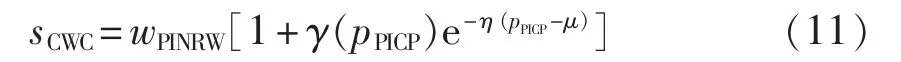
其中，μ由PICP预先定义；η为一个超参数，用于放大PICP和μ之间的差异性；如果对预先定义的PICP不满意，CWC在这方面以指数形式做惩罚；如果对预先定义的PICP满意，更加关注预测区间的宽度将更合理。因此，对于测试样本，γ（pPICP）为一个阶梯函数，它的值由PICP的满意度决定：

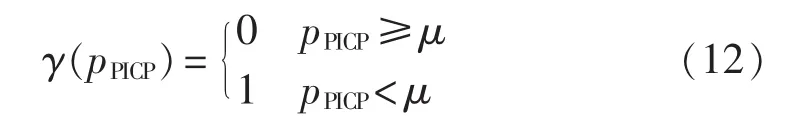
图1为粒子群优化算法［19］构造预测区间的流程。

2 算例分析

2.1 变压器油中溶解特征气体

变压器中绝缘油和固体绝缘材料在电或热的作用下会逐渐老化和分解产生相应的气体，变压器不同的绝缘故障类型［20］使得油中溶解气体的成分和含量也不同。其中对变压器绝缘故障诊断分析有作用的特征气体主要有氢气、甲烷、乙炔、乙烯、乙烷、一氧化碳、二氧化碳等（下文中关联度矩阵中的数据亦按此顺序对应）。

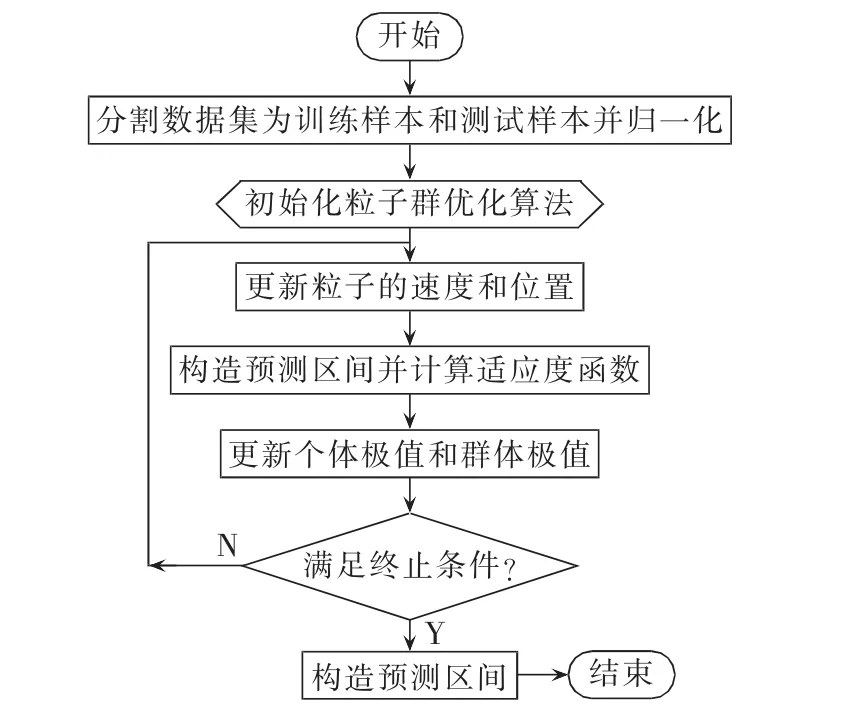
图1 利用粒子群优化算法构造预测区间Fig.1 Prediction interval construction by particle swarm optimization algorithm

2.2 区间预测模型求解步骤

a.通过式（3）对内部相关因素与待预测状态量的关联度进行分析，将关联度高的因素输入各点预测模型的训练样本中；

b.通过式（6）得到各单一预测模型的客观权重，建立基于关联度和熵理论的组合预测模型，对油中溶解气体含量进行点预测；

c.利用粒子群优化算法对预测区间的综合评价指标式（11）进行优化，得到最优的比例系数，通过式（7）构造油中溶解气体浓度的预测区间。

2.3 点预测方法评价指标

为了能对点预测的结果进行比较分析，本文采用点预测的百分比平均相对误差和最大相对误差来评价预测模型的精度，分别定义为：

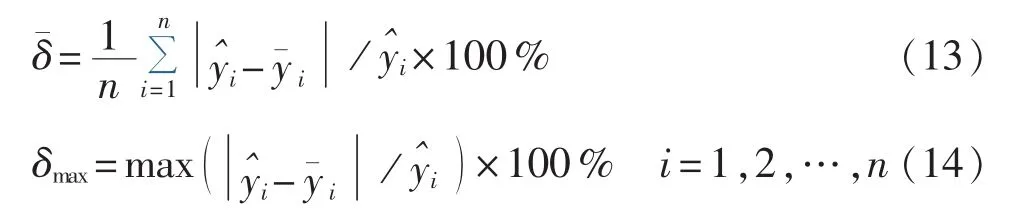
其中，为点预测值；n为未来样本点数量。

2.4 实例分析

本文采用浙江省某500kV变压器的油色谱数据［2］进行实测分析。待预测状态量以氢气为例，应用2004年1月至2009年1月的数据建立预测模型，应用2009年4月至2010年1月的数据来说明本文所提的区间预测方法的有效性。

由MATLAB编程计算得到的关联度矩阵为R=［0.585 0.653 0.593 0.629 0.584 0.708］，即氢气浓度与乙炔、乙烷和二氧化碳浓度的关联度较大，因此将这3种气体的数据样本输入预测模型的训练样本中。

利用关联度分析确定关联影响因素后，再利用熵权法确定各预测模型的权重，由式（6）确定权重矩阵W=［0.2964 0.3906 0.3130］（数据分别与 RBFNN、LSSVM和GM法对应），最终得到基于熵的组合预测模型，继而得到组合预测方法下氢气浓度未来的变化趋势。

图2给出了本文组合预测模型对变压器油中溶解的氢气浓度预测误差样本的概率分布直方图。由图2可见，预测误差样本的分布不完全服从正态分布，同时利用SPSS软件中的多种正态分布检验工具也均证实氢气浓度的预测误差样本为非正态分布。但本文的方法无论误差样本是否服从正态分布，均可构造一定置信水平下溶解气体的预测区间，并不受传统区间预测方法中服从正态分布的限制。

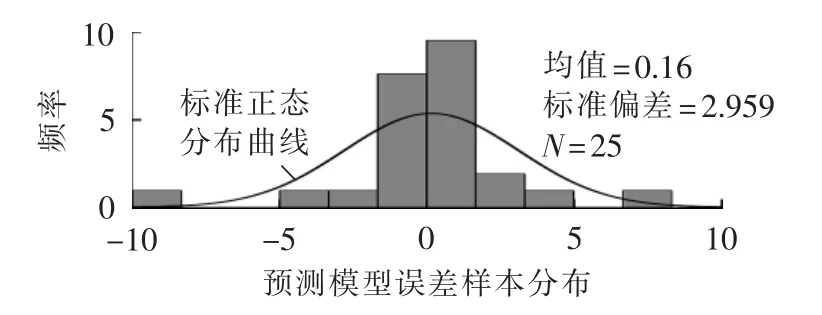
图2 预测误差样本概率分布直方图Fig.2 Histogram of probability distribution of prediction error samples

图3为是否考虑关联因素的熵组合预测模型对氢气浓度变化趋势的对比预测，其中基于熵的组合预测均结合了RBFNN、LSSVM和GM 3种方法。由图3可知，本文的组合预测模型与未考虑关联因素的熵组合预测模型相比，预测精度有所提升，因而能较好地拟合氢气浓度的发展趋势。

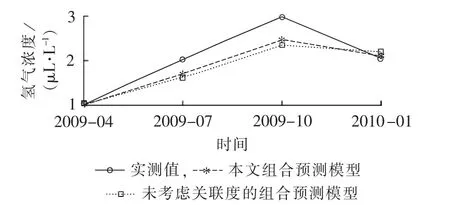
图3 氢气浓度的预测结果Fig.3 Results of H2concentration prediction

图4所示为CWC的迭代过程。由图4可见，CWC在迭代124次后稳定在0.567。

图5所示为95%置信水平（即μ=0.95）下构造的氢气浓度预测区间。迭代结束后得到的最优的比例系数分别为α=0.2136，β=0.0291。

未考虑关联因素的单一预测方法（RBFNN、LSSVM、GM）、基于熵的组合预测方法（CP1）和本文的组合预测方法（CP2）的预测结果见表1。其中，组合预测均是综合以上3种单一预测模型。从表1可见，本文组合预测方法的平均相对误差（8.04%）和最大相对误差（16.21%）均小于其他点预测模型的误差；氢气浓度在各时间点的预测区间在95%置信水平下完全覆盖了氢气浓度的实测值，且预测区间上界捕捉到了氢气浓度向上的波动，下界捕捉到了最后一个样本点向下的波动。

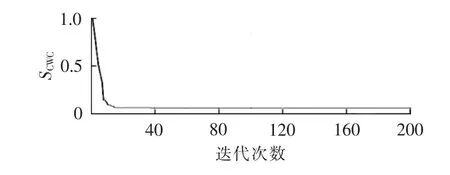
图4 CWC的迭代过程Fig.4 Iterative process of CWC

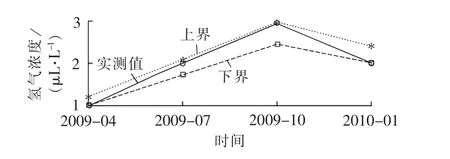
图5 氢气浓度的预测区间Fig.5 Predicted interval of H2concentration

表1 各预测模型的预测结果Table 1 Predicted results by different prediction models

3 结论

本文首先应用灰色关联度分析方法确定了内部各因素的影响程度，并建立了基于熵的组合预测模型，在此基础上构造了油浸式变压器油中溶解气体浓度的区间预测模型。以浙江省某500 kV变压器的油色谱数据样本建模分析并得到如下结论：

a.通过对变压器油中溶解的各气体浓度进行关联度分析，确定了各影响因素对待预测状态量的影响程度，并将关联度较高的因素用于单一预测模型的构造，提高了单一预测模型的预测精度；

b.在考虑关联因素的影响后，将RBFNN、LSSVM和GM 3种单一预测方法进行组合，并利用熵权法确定了组合预测模型的客观权重，此组合预测模型的精度相较于单一预测模型有了较大的提高；

c.利用比例系数法和粒子群优化算法在本文已构建的组合点预测模型的基础上，建立了一定置信水平下变压器油中溶解气体浓度的区间预测模型，解决了传统区间预测方法中预测误差样本必须服从正态分布的问题，所构造的预测区间有效捕捉到了氢气浓度的波动。

本文的方法相比传统区间预测仍是基于点预测来构造预测区间，然而点预测始终不能做到无偏估计，因此不依赖点预测模型构造预测区间是下一步将要研究的重点。

参考文献：

［1］方隽.变压器状态检修的研究与应用［D］.杭州：浙江大学，2008.FANG Jun.Research ofco ndition based maintenance and application on transformer［D］.Hangzhou：Zhejiang University，2008.

［2］陈安伟.输变电设备状态检修［M］.北京：中国电力出版社，2012：149-153.

［3］王晓兰，葛鹏江.基于相似日和径向基函数神经网络的光伏阵列输出功率预测［J］.电力自动化设备，2013，33（1）：100-103.WANG Xiaolan，GE Pengjiang.PV array output power forecasting based on similar day and RBFNN［J］.Electric Power Automation Equipment，2013，33（1）：100-103.

［4］刘文霞，徐晓波，周樨.基于支持向量机的纯电动公交车充/换电站日负荷预测［J］.电力自动化设备，2014，34（11）：41-47.LIU Wenxia，XU Xiaobo，ZHOU Xi.Daily load forecasting based on SVM for electric bus charging station［J］.Electric Power Automation Equipment，2014，34（11）：41-47.

［5］张哲，赵文清，朱永利.基于支持向量机回归的电力变压器状态评估［J］.电力自动化设备，2010，30（4）：81-84.ZHANG Zhe，ZHAO Wenqing，ZHU Yongli.Powertransformer condition evaluation based on supportvector regression［J］.Electric Power Automation Equipment，2010，30（4）：81-84.

［6］赵文清，朱永利，张小奇.基于改进型灰色理论的变压器油中溶解气体预测模型［J］.电力自动化设备，2008，28（9）：23-26.ZHAO Wenqing，ZHU Yongli，ZHANG Xiaoqi.Prediction model for dissolved gas in transformer oil based on improved grey theory［J］.Electric Power Automation Equipment，2008，28 （9）：23-26.

［7］孙德忠，喻登科，田野.一种基于专家组合多重相关的主观赋权方法［J］.统计与决策，2012（19）：88-90.SUN Dezhong，YU Dengke，TIAN Ye.A multiple correlation of subjective weightmethod based on combination experts［J］.Statistics&Decision，2012（19）：88-90.

［8］杨锡运，刘欢，张彬，等.组合权重相似日选取方法及光伏输出功率预测［J］.电力自动化设备，2014，34（9）：118-122.YANG Xiyun，LIU Huan，ZHANG Bin，et al.Similarday selection based on combined weight and photovoltaic power output forecasting［J］.Electric Power Automation Equipment，2014，34（9）：118-122.

［9］杨廷方，周力行，李景禄，等.基于最优权重的组合模型诊断变压器故障［J］.电网技术，2013，31（1）：190-194.YANG Tingfang，ZHOU Lixing，LI Jinglu，et al.Power transformer fault diagnosis based on optimal weights combined model［J］.Power System Technology，2013，37（1）：190-194.

［10］卞建鹏，廖瑞金，杨丽君.应用弱化缓冲算子与最小二乘支持向量机的变压器油中溶解气体浓度预测［J］.电网技术，2012，36（2）：195-199.BIAN Jianpeng，LIAO Ruijin，YANG Lijun.Concentration prediction of gases dissolved in transformer oil based on weakening buffer operator and least square support vector machine ［J］.Power System Technology，2012，36（2）：195-199.

［11］KHOSRAVI A，NAHAVANDI S，CREIGHTON D.Construction of optimal prediction intervals for load forecasting problems［J］.IEEE Trans on Power Systems，2010，25（3）：1496-1503.

［12］LIU W H.Forecasting the semiconductor industry cycles by bootstrap prediction intervals［J］.Appl Econ，2007，39（13）：1731-1742.

［13］罗毅，李昱龙.基于熵权法和灰色关联分析法的输电网规划方法综合决策［J］.电网技术，2013，37（1）：77-81.LUO Yi，LI Yulong.Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis［J］.Power System Technology，2013，37（1）：77-81.

［14］齐敏芳，付忠广，景源，等.基于信息熵与主成分分析的火电机组综合评价方法［J］.中国电机工程学报，2013，33（2）：58-64.QI Minfang，FU Zhongguang，JING Yuan，et al.A comprehensive evaluation method of power plant units based on information entropy and principal component analysis［J］.Proceedings of the CSEE，2013，33（2）：58-64.

［15］王娟.基于信息熵-灰色局势集的企业战略决策方法［J］.统计与决策，2014（4）：173-175.WANG Juan.Decision method of enterprise strategy based on information entropy and grey situation set［J］.Statistics&Decision，2014（4）：173-175.

［16］DYBOWSKIR，GANT V.Clinicalapplicationsofartificial neural networks［M］.Cambridge，UK：Cambridge University Press，2001：298-326.

［17］KHOSRAVI A，NAHAVANDI S，CREIGHTON D，et al.A lowerupperbound estimation method forconstruction ofneural network based prediction intervals［J］.IEEE Trans on Neural Network，2011，22（3）：337-346.

［18］KHOSRAVI A，NAHAVANDI S，CREIGHTON D，et al.Interval type-2 fuzzy logic systems for load forecasting：a comparative study［J］.IEEE Trans on Power Systems，2012，27（3）：1274-1282.

［19］胡旺，李志蜀.一种更简化而高效的粒子群优化算法［J］.软件学报，2007，18（4）：861-868.HU Wang，LI Zhishu.A simpler and more effective particle swarm optimization algorithm［J］.Journal of Software，2007，18（4）：861-868.

［20］梁帅伟.抗老化变压器油及其对绝缘纸热老化影响的研究［D］.重庆：重庆大学，2009.LIANG Shuaiwei.Study on antioxidation transformer insulation oil and its effects on oil-immersed paper thermal aging［D］.Chongqing：Chongqing University，2009.

［21］顾雪平，赵宝斌，刘文轩.结合多目标优化与灰色关联决策的负荷恢复方法［J］.电力自动化设备，2015，35（9）：6-13.GU Xueping，ZHAO Baobin，LIU Wenxuan.Load restoration based on multi-objective optimization and grey incidence decisionmaking［J］.Electric Power Automation Equipment，2015，35（9）：6-13.