基于奇异值熵和潮流分布熵的电网关键节点辨识
王 涛,岳贤龙,顾雪平,张 尚,赵宝斌
(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
0 引言
近年来,全球范围内发生的大停电事故[1-4]给人们带来了巨大的损失,造成了极为严重的社会影响和经济损失。这些事故有的是因多变的气候等外部因素引起的,有的是因电网自身的缺陷等内部因素引起的,其均与电网的关键节点具有紧密的联系。因此,为了减少大停电事故的发生,迫切需要在系统当前运行状态下,及时、准确地辨识出对电网连锁故障的传播起推波助澜作用的关键节点。
目前,对于关键节点辨识分析的相关研究取得了一些成果,但仍没有广泛认可的评估模型和评估指标,一方面,对图论方法进行改进,以提高其在电网中的适用性;另一方面,引入与电力系统相关的参量,以适用于实际电网的应用。文献[5-6]利用节点或支路的介数衡量节点或支路的关键性;文献[7]基于小世界网络理论提出输电线路的介数值指标对电网进行脆弱性评估;文献[8-9]基于复杂网络理论对电网的脆弱线路进行辨识;文献[10]基于复杂网络理论和有向权重图辨识出大型电力系统中的薄弱节点和薄弱线路。以上研究从网络结构角度评估电网脆弱区域,但仅考虑网络拓扑的方法对系统的评估略显粗糙,不能体现节点与支路之间相互作用的电气关系,难以满足大型互联电网应用的实际需求。
针对基于网络结构模型分析的缺陷,越来越多的研究引入电气参数对其进行改善。文献[11-12]提出电气介数指标和网络效能指标对系统脆弱环节进行识别,但是在指标处理过程中对参数进行了较多的假设;文献[13]基于网络最大流和复杂网络理论对电网进行关键节点辨识;文献[14]和[15]分别利用源流路径电气剖分信息和功率输送关系,并结合网络结构及系统运行状态辨识电网中的关键环节;文献[16]引入系统最小失负荷率表征网络的传输效率,并结合N-k故障时故障集的脆弱性识别关键线路;文献[17]利用节点电气耦合连接度辨识电力系统复杂网络中的关键节点,并利用异质网络理论分析了电网的动力学特性。上述文献分别综合了不同的电气参量,更加贴近于实际电网模型。
熵反映了一种自然界现象有序程度演化的规律,以其独特的内涵和渗透力被广泛应用于度量复杂系统的不确定性、稳定程度。对于电力系统而言,熵既可以定量描述系统潮流的分布情况,又可以在一定程度上揭示系统运行状态的脆弱性[18]。文献[19]改进了文献[18]中的方法,重新定义了潮流分布熵和潮流转移熵,提高了对电网脆弱性评估的准确性;文献[20]引入线路负载率对潮流转移熵进行改进,更加符合实际电力系统的要求;文献[21]基于潮流熵提出了复杂电网自组织临界态判断模型,从总体平均负载率的角度进行判断,并未定量地对电网的脆弱性进行评估;文献[22]基于熵度和网络能力,提出了一种扩展的拓扑方法评估电网脆弱性。以上基于潮流的熵指标能反映扰动冲击后系统潮流的分布情况,但仍缺少利用熵理论从节点电压幅值角度出发,考虑节点负荷变化对系统稳定带来的影响。
本文从熵理论出发,综合考虑奇异值熵和潮流分布熵辨识电力系统中的关键节点。奇异值熵反映了节点负荷变化对系统中节点电压幅值的影响,电压幅值的变化体现了对系统静态电压稳定性的影响;潮流分布熵表征了节点负荷变化对系统中线路潮流分布的影响,两者共同从电气学的角度解释了节点负荷变化对系统带来的威胁。此外,基于系统平均负载率和电力系统的能量熵提出了系统安全指标,以便于通过对节点的连续攻击验证本文所提方法的有效性和正确性。最后,以IEEE 39节点系统和河北南网系统作为算例进行仿真分析,验证了定义的节点综合评估指标在复杂电网关键节点辨识中的重要作用。
1 关键节点综合评估指标
1.1 熵理论
熵是对系统无序和混乱状态的一种度量,是一门应用十分广泛的科学理论,其在信息科学、系统科学、生命科学与管理科学等众多领域均取得了丰硕成果[18,21]。 熵理论起源于热力学定律,用于测量在动力学方面不能做功的能量总数,逐渐推广到其他学科,物理学中用于度量系统内部分子运动的混乱程度,信息学中用来描述离散系统不确定性的度量。
对于广义的复杂系统,熵能够描述系统的稳定程度,系统的混乱程度越高,系统熵值越大;系统状态越有序,系统熵值越小[20]。系统熵值定义如下:
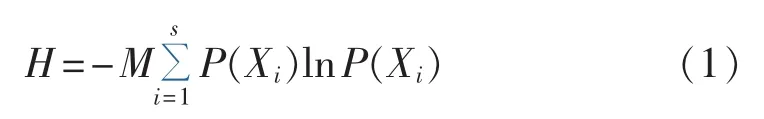
其中,M为常数;s为系统的状态数;P(Xi)为状态 Xi出现的概率。
由式(1)可知,如果系统仅有一个状态,出现概率为 1,系统为最有序运行状态,熵值为 0[23];如果系统有s个运行状态,且出现概率相同,系统为最混乱运行状态,熵值为lns。
1.2 系统模型
对于有n个独立节点、l个PV节点的电力系统,潮流方程的极坐标形式为[24]:

其中,i=1,2,…,n;j=1,2,…,n;Pi和 Qi分别为节点注入有功、无功功率;Ui和Uj为节点电压幅值;Gij和Bij为节点导纳矩阵中的元素;θij为电压相角差。
式(2)中的各参数可以划分为状态变量与控制变量 2 种,状态变量表示为 X= [UL,δL,δg]T,控制变量表示为 μ=[PL,QL,Pg,Ug,Uv,δv]T,其中,UL、δL、PL和QL分别表示PQ节点电压、节点电压相角、节点注入有功和无功功率,δg、Pg、Ug分别表示 PV 节点电压相角、节点注入有功功率和节点电压,Uv、δv分别表示平衡节点电压和电压相角。
将式(2)用泰勒级数展开,得到矩阵形式表示的修正方程式为:
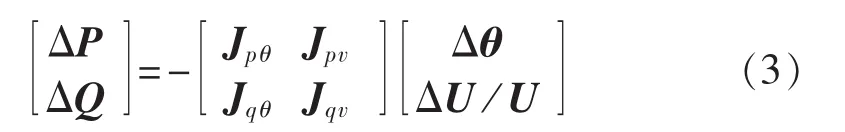
雅可比矩阵J的各元素可表示为:
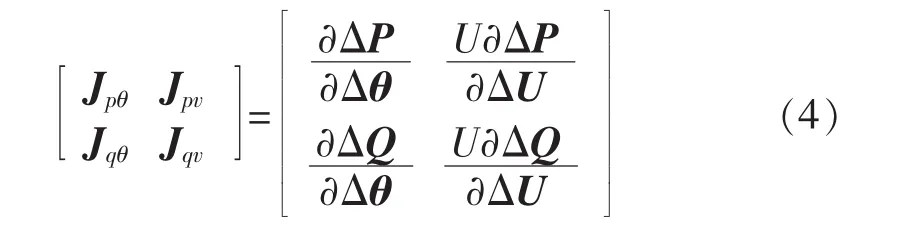
其中,Jpθ、Jpv、Jqθ、Jqv均可看作式(2)中状态变量对控制变量灵敏度的倒数,Jpθ和Jpv分别反映节点有功功率变化对系统中节点电压相角和幅值的影响,Jqθ和Jqv分别反映节点无功功率变化对系统中节点电压相角和幅值的影响。
1.3 奇异值熵的定义
奇异值是矩阵固有的特征[25],具有较好的稳定性,如果矩阵中元素发生变化,奇异值将发生变化。在电力系统等复杂系统中,当运行状态发生改变时,对应雅可比矩阵的奇异值将随之改变[26-27]。因此,为了定量描述系统状态的变化程度,基于信息熵的理论引入奇异值熵,以此表征不同扰动对系统稳定带来的影响程度。
对式(4)的雅可比矩阵J进行奇异值分解可得:
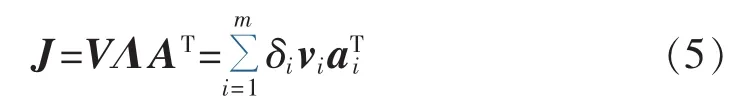
其中,若JϵRm×m,则V和A 均为m×m的正交矩阵,Λ为奇异值 δi(i=1,2,…,m)组成的非负对角阵,vi和 ai分别为V和A中δi对应的列向量。
由式(3)和式(5)可得:

式(6)中,当δi较小且几乎为零时,节点有功和无功功率的变化将引起节点电压幅值和相角的较大变化,此时,若系统处于弱稳定状态,将进一步加重系统的危险性;若节点电压接近于崩溃点,将对系统的安全运行构成较大的威胁。
对式(5)中Λ包含的元素进行归一化处理:

那么,根据信息熵的定义,雅可比矩阵J的奇异值熵可定义为:

由熵的定义可知,当ei均相等时,奇异值熵HΛ达到最大值lnm,此时各节点负荷变化引起的节点电压幅值和相角的变化越一致,从而对系统的冲击越均衡;反之,当Λ中仅有一个元素值不为0时,奇异值熵HΛ为最小值0,由式(6)可知,此时系统中节点负荷的微弱变化将会引起系统中节点电压幅值和相角的剧烈变化,对系统的冲击最大,极易引起支路越限故障。
HΛ对节点i有功功率Pi变化的灵敏度定义为:
HΛi越大,节点i有功功率Pi的变化引起HΛ的变化越大,说明Λ中元素的有序性变化越大,各奇异值发生较大的变化,此时,节点负荷的变化会引起系统中节点的电压幅值和相角较大差异程度的波动,而电压幅值的变化体现了对系统静态电压稳定性的影响,对应δi较小的节点负荷的波动将引起节点电压幅值和相角的较大变化,从而对系统的安全运行造成较大的威胁。反之,HΛi越小,节点i有功功率Pi的变化引起HΛ的变化较小,说明Λ中元素的有序性变化越小,节点负荷的变化不会引起系统中节点的电压幅值和相角发生剧烈的波动,系统的运行状态不会发生较大的变化,对系统安全运行造成的影响越小。
1.4 潮流分布熵的定义
节点负荷的变化不仅影响节点电压幅值和相角,同样会引起系统中线路负载率的变化。然而,线路受到热稳定极限的约束,如果线路处于重载状态,因保护动作将引起线路切除,此时,为了维持输电平衡,系统将发生较大的潮流转移,而大规模的潮流转移是引起电网连锁过载的重要因素[28-30]。
系统在正常运行状态下,当节点i发生单位负荷变化时,线路k上的潮流变化量为:

其中,为线路k的初始潮流;为节点i单位负荷冲击后线路k的潮流。
正常运行状态下,节点i单位负荷变化对系统潮流冲击总量为:

其中,C为系统中线路总数。
线路k因节点i单位负荷变化所引起潮流转移的冲击比率为:

式(12)中满足信息熵归一化的条件,那么,节点i发生单位负荷变化时系统的潮流分布熵为:

HTi越大,节点i负荷变化后,系统潮流冲击在线路上的潮流分布越均匀,对系统线路的潮流冲击越小;反之,HTi越小,系统潮流冲击在线路上的分布越不均匀,容易聚集在少数线路上,对线路的潮流冲击越大,极易引起线路过载,对系统安全运行造成的影响较大。
1.5 关键节点综合评估指标
奇异值熵表征了节点负荷变化对系统中节点电压幅值的影响程度,潮流分布熵表征了节点负荷变化对系统中线路负载率的影响。无论是电压越限还是线路过载,均可能引起系统连锁性故障,最终导致电网大面积停电。因此综合奇异值熵及潮流分布熵构建关键节点综合评价指标。
由式(9)和式(13)可知,节点对应的奇异值熵越大,该节点负荷变化对系统的冲击越大;节点对应的潮流分布熵越小,该节点负荷变化对系统的潮流冲击越大。因此,关键节点综合评估指标可定义为:

其中,Hi为节点i的综合评估指标;wT为节点的潮流分布熵影响权重因子;H′Ti为归一化后节点i对应的潮流分布熵;wΛ为节点的奇异值熵影响权重因子;H′Λi为归一化后节点i对应的奇异值熵;n为电力系统中节点总数。
式(14)中,权重系数需利用文献[31]中基于熵的客观权重法分别确定其值的大小,并进行归一化处理。应用于在线监控系统时,权重系数也可依据调度经验或系统实际工况进行适当调整。Hi越小,节点i的负荷变化对系统的影响越大,节点越关键,需要系统运行人员重点监视;反之,节点i对系统安全运行的影响越小。
2 关键节点的辨识流程
本文基于奇异值熵和潮流分布熵分析节点的负荷变化对系统安全运行的影响,因此,在分析过程中主要评估系统中PQ节点的关键性。关键节点的辨识流程如图1所示。
该方法主要包括以下步骤:
a.读取系统安全运行状态下的数据,对系统中PQ节点i进行单位负荷冲击,并计算冲击后的系统潮流;
b.分别计算节点i的奇异值熵和潮流分布熵,根据式(14)计算节点i的综合评估指标;
c.判断是否遍历完所有节点,若满足,则转到步骤d,否则转到步骤a;
d.依据各节点的综合评估指标进行排序,获取系统中的关键节点。

图1 关键节点仿真基本流程Fig.1 Basic flowchart of critical node simulation
3 关键节点的攻击分析
为了分析本文方法计算得到关键节点排序的正确性,定义系统安全指标来表征系统安全状态,并对系统中的节点分别进行连续性攻击,从而得到不同攻击对系统安全的影响程度。系统潮流的平均负载率是影响系统连锁故障传播的重要因素之一[32-33],它能够在整体上反映系统的负载水平,却不能够表征因潮流无序分布对电网连锁故障带来的影响程度,而电力系统的能量熵可以描述系统在某一确定状态下内部能量的分布规律,进而度量系统的稳定性[18],因此,可以综合系统的平均负载率和电力系统的能量熵共同描述系统的安全状态。
系统的平均负载率定义为[34]:

其中,ηi为系统状态i下系统的平均负载率;C为系统中线路总数;Pki为系统状态i下线路k上的潮流;Pkmax为线路k的最大有功传输容量。
系统状态i下线路k的负载率为:

其中,k=1,2,…,C。
对式(18)中的μki进行归一化处理,可得:

其中,μ′ki为μki归一化后的结果,满足信息熵归一化的条件。
那么,系统状态i下电力系统的能量熵[18]定义为:

系统的平均负载率越小,系统相对安全水平越高;反之,系统安全水平越低,越容易接近临界状态。然而,电力系统的能量熵越小,线路负载率分布的一致性越差,此时高负载率的线路对系统的连锁故障威胁较大,更容易引发连锁故障;反之,线路负载率分布越均匀,容量大的线路将承载较大的潮流,容量小的线路将承载较小的潮流,系统安全性越好。因此,结合式(17)和式(20),可定义系统状态 i下的安全指标为:

上式中Vi越小,系统安全性越好;反之,系统安全性越差。
4 算例分析
分别以IEEE 39节点系统和河北南网系统为算例,采用Matpower进行仿真计算,验证本文关键节点辨识方法的有效性和正确性。
4.1 IEEE 39节点系统
IEEE 39节点测试系统含有10个PV节点和28个PQ节点,节点31为平衡节点,系统如图2所示。

图2 IEEE 39节点系统接线图Fig.2 Wiring diagram of IEEE 39-bus system
根据文献[31]中熵的客观权重法,并考虑到与节点电压变化引起的严重度相比,支路潮流更易过载而退出运行[35-36],实验中求得到节点奇异值熵影响权重因子为0.4,节点潮流分布熵影响权重因子为0.6。利用第1节中的综合评估指标对系统中所有节点进行排序,排序最高的10个节点信息如表1所示。
从表1可以看出,排序前10的节点中,除了节点29外,其余的9个节点分布较为集中,说明了该集中区域在系统中较为关键,需要系统运行人员重点监视。对于节点29,它的潮流分布熵最大,对线路过载影响较小;而它的奇异值熵相对较小,对系统中其他节点的电压幅值和相角的影响相比更大,可能因与平衡节点31电气距离较大有关。

表1 IEEE 39节点系统的关键节点Table 1 Critical nodes of IEEE 39-bus system
鉴于许多文献中采用IEEE 39节点系统进行仿真分析,可以将本文的仿真结果与其他文献所得结果进行对比分析。文献[18]主要采用潮流分布熵,文献[37]主要采用灵敏度辨识系统中的关键节点,采用不同方法的对比结果如表2所示。

表2 关键节点辨识结果对比Table 2 Comparison of identified critical nodes among different identification methods
由表2可知,本文方法前10个关键节点中有6个与文献[18]和文献[37]方法的结果均相同,分别为节点 6、8、7、5、11、13。 前 4 个节点相同,仅仅排序不完全相同,可以确定系统中5、6、7、8所在的区域非常关键。节点4与灵敏度方法的结果相同,节点9和节点14也在潮流熵方法的结果中,排序的差异主要是由于不同方法的评估指标所考虑的侧重点不同造成的。
此外,根据第3节中的方法对节点负荷进行连续攻击实验,并观察系统安全指标Vi的变化情况,以便于分析节点负荷变化带给系统的影响。对IEEE 39节点系统中的每个PQ节点分别以10 MW为增长速度逐次增加,直至系统中线路负载率达到0.8,即线路出现了重载情况,相当于实际系统中将会出现线路因保护动作而退出运行的情况,则停止增加负荷。对仿真结果中排序前4的节点与节点11、13分别单独进行上述的攻击,以便形成对比,不同攻击后系统安全指标的变化结果如图3所示。

图3 不同节点攻击后的IEEE 39节点系统状态变化Fig.3 Safety index variation of IEEE 39-bus system for different nodes attacked
图3中,随着节点负荷的增加,对应的系统安全指标不停地波动,变化趋势一致。节点6对应的系统安全指标相对较大,致使系统安全性较差;节点7与节点8对应的系统安全指标几乎一致地进行波动,表明它们的重要程度几乎相同,对应了它们在仿真结果中的排列顺序;节点11与节点13在仿真结果中分别排序第7和第8,与节点7和节点8的分析一样,说明了它们的重要性较接近。从总体来看,排序前4的节点对系统的影响基本相同,而排序靠后的节点对系统的影响相对较小,说明利用本文所提出方法获取的评估结果是准确的。
4.2 河北南网系统
为了进一步验证本文关键节点辨识模型的有效性,对河北南网系统进行仿真分析,选定的系统含有36个PV节点和232个PQ节点,上安电厂节点为平衡节点。
利用第1节中的综合评估指标对该系统中所有500 kV节点进行排序,排序最高的前10个节点信息如表3所示。

表3 河北南网系统的关键节点Table 3 Critical nodes of Southern Hebei Power System
对照河北南网系统接线图,石北站是石家庄地区的枢纽变电站;沧西站是沧州地区的枢纽变电站;廉州站处于石家庄地区和邯邢地区的输电通道上;慈云站主供高碑店、豆庄、涿州、涞阳、里营5座220 kV变电站;彭村站是邢台地区重要枢纽站;保北站是保定地区枢纽站,也处于山西电网到河北南网的输电断面上。辛安站是邯郸地区核心站,并经由辛聊线连接山东电网。辛集站是石家庄地区和沧州地区间重要变电站,并连接了长召、陈庄、范庄3座220 kV变电站。清苑站是石家庄地区和保定地区间枢纽站,并承担了定州电厂电力外送的任务。广元站连接了彭村站、辛安站和邢南电厂,是邯邢地区内的重要变电站。因此,从拓扑角度来看,选定的关键节点与河北南网的实际相符合。
与第4.1节中对IEEE 39节点的攻击相似,对500 kV节点负荷以5 MW为增长速度进行连续攻击实验。对仿真结果中排序前3的石北站、沧西站、廉州站和排序较后的清苑站、广元站分别单独进行上述的攻击,以便形成对比,不同攻击后系统安全指标的变化结果如图4所示。
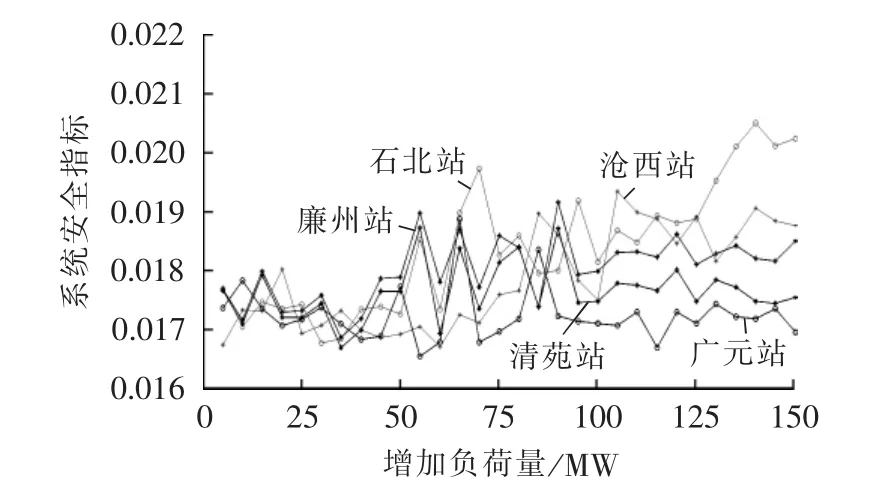
图4 不同节点攻击后的河北南网系统状态变化Fig.4 Safety index variation of Southern Hebei Power System for different nodes attacked
由图4可以看出,随着节点负荷的增加,对应的系统安全指标在100 MW之前不停地波动,变化趋势近似,说明在一定波动范围内各节点对系统的安全威胁相差较小;但是在大于100 MW之后,不同节点负荷的变化对系统的影响有了相对明确的差别,石北站影响最大,沧西站和廉州站仍有部分交叉,它们的关键程度相近;清苑站和广元站相比于上述3个节点对系统威胁较小。对照河北南网实际运行分析,石北站是山西电网经阳北线及忻石线对河北南网送电的枢纽变电站,也是河北南网石家庄地区连接保定地区的核心变电站,一旦退出运行会造成河北南网重大事故。沧州西部地区主要由沧西站和任丘电厂供电,一旦退出运行,会造成沧州西部8座220 kV变电站全停,损失负荷约1300 MW,构成一般电网事故。廉州站处于石家庄地区和邯邢地区的重要输电通道上,其退出运行会造成沧东线过载28%,需要石家庄南部地区在事故时限电550 MW。通过以上分析可知,本文方法辨识出的关键节点符合系统的实际运行情况,进一步验证了该方法的合理性。
5 结论
电力系统中关键节点的辨识对连锁故障防控具有重要的意义。本文从节点负荷变化对系统节点电压幅值和相角,以及对线路潮流负载率两方面的影响考虑,基于奇异值熵与潮流分布熵提出节点的综合评估指标,据此识别系统中的关键节点,从电气的角度结合电网的运行状态进行分析,更加符合电力系统的实际情况。通过对IEEE 39节点系统与河北南网系统算例的测试,识别出了电网中的关键节点,并对节点进行连续攻击,利用定义的系统安全指标验证了所提方法的有效性和正确性,对系统运行人员辨识重点监视区域有重要的实用价值。
参考文献:
[1]CAMERAS A,LYNCH V E,DOBSSON I,et al.Complex dynamics of blackouts in power transmission system[J].Chaos,2004,14(3):643-652.
[2]印永华,郭剑波,赵建军,等.美加“8.14”大停电事故初步分析以及应吸取的教训[J].电网技术,2003,27(10):8-11,16.YIN Yonghua,GUO Jianbo,ZHAO Jianjun,etal.Preliminary analysis of large scale blackout in interconnected North America power grid on August 14 and lessons to be drawn [J].Power System Technology,2003,27(10):8-11,16.
[3]India Grid Disturbance Enquiry Committee.Report of the enquiry committee on grid disturbance in northern region on 30th July 2012 and in northern,eastern& north-eastern region on 31st July 2012[R].New Delhi,India:India Ministry of Power,2012.
[4]U.S.-Canada Power System Outage Task Force.Final report on the August 14,2003 blackout in the United States and Canada:causes and recommendations[R].Washington DC,USA:U.S.Department of Energy,2004.
[5]MOTTER A E,LAI Y C.Cascade-based attacks on complex networks[J].Physical Review E,2002,66(6):065102.
[6]KINNEY R,CRUCITTI P,ALBERT R,et al.Modeling cascading failures in the North American power grid[J].The European PhysicalJournalB-Condensed Matterand ComplexSystems,2005,46(1):101-107.
[7]刘耀年,术茜,康科飞,等.基于电抗加权介数指标的电网脆弱线路识别[J].电力系统保护与控制,2011,39(23):89-92.LIU Yaonian,SHU Xi,KANG Kefei,etal.Identification of vulnerable lines in power grid based on the weighted reactance betweenness index[J].Power System Protection and Control,2011,39(23):89-92.
[8]曹一家,陈晓刚,孙可.基于复杂网络理论的大型电力系统脆弱线路辨识[J].电力自动化设备,2006,26(12):1-5,31.CAO Yijia,CHEN Xiaogang,SUN Ke.Identification of vulnerable lines in powergrid based on complex network theory[J].Electric Power Automation Equipment,2006,26(12):1-5,31.
[9]苏慧玲,李扬.基于电力系统复杂网络特征的线路脆弱性风险分析[J].电力自动化设备,2014,34(2):101-107.SU Huiling,LI Yang.Line vulnerability risk analysis based on complex network characteristics of power system [J].Electric Power Automation Equipment,2014,34(2):101-107.
[10]张国华,张建华,杨京燕,等.基于有向权重图和复杂网络理论的大型电力系统脆弱性评估[J].电力自动化设备,2009,29(4):21-26.ZHANG Guohua,ZHANG Jianhua,YANG Jingyan,et al.Vulnerability assessmentofbulk powergrid based on weighted directional graph and complex network theory[J].Electric Power Automation Equipment,2009,29(4):21-26.
[11]何俊,庞松龄,禹冰,等.基于容量介数指标的电网脆弱线路识别[J].电力系统保护与控制,2013,41(8):30-35.HE Jun,PANG Songling,YU Bing,et al.Vulnerable line identification of power grid based on capacity betweenness index[J].Power System Protection and Control,2013,41(8):30-35.
[12]王仁伟,张友刚,杨阳,等.基于电气介数的复杂电网脆弱线路辨识[J].电力系统保护与控制,2014,42(20):1-6.WANG Renwei,ZHANG Yougang,YANG Yang,et al.Vulnerable line identification of complex power grid based on electrical betweenness[J].Power System Protection and Control,2014,42(20):1-6.
[13]鞠文云,李银红.基于最大流传输贡献度的电力网关键线路和节点辨识[J].电力系统自动化,2012,36(9):6-12.JU Wenyun,LIYinhong.Idectification ofcriticallinesand nodesin powergrid based on maximum flow transmission contribution degree[J].Automation of Electric Power Systems,2012,36(9):6-12.
[14]邵莹,于继来.采用源流路径电气剖分信息的电网脆弱性评估[J].中国电机工程学报,2009,29(31):34-39.SHAO Ying,YU Jilai.Power grid vulnerability assessment based on electrical dissection information of the electric power network[J].Proceedings of the CSEE,2009,29(31):34-39.
[15]王涛,高成彬,顾雪平,等.基于功率介数的电网关键环节辨识[J].电网技术,2014,38(7):1907-1913.WANG Tao,GAO Chengbin,GU Xueping,et al.Power betweenness based identification ofpowergrid criticallinks [J].Power System Technology,2014,38(7):1907-1913.
[16]李扬,苏慧玲.N-k故障下影响电力系统脆弱性的关键线路研究[J].电力自动化设备,2015,35(3):60-67.LIYang,SU Huiling.Criticalline affecting powersystem vulnerability under N-k contingency condition [J].Electric Power Automation Equipment,2015,35(3):60-67.
[17]谭玉东,李欣然,蔡晔,等.基于电气距离的复杂电网关键节点识别[J].中国电机工程学报,2014,34(1):146-152.TAN Yudong,LI Xinran,CAI Ye,et al.Critical node identification for complex power grid based on electricaldistance [J].Proceedings of the CSEE,2014,34(1):146-152.
[18]李勇,刘俊勇,刘晓宇,等.基于潮流熵的电网连锁故障传播元件的脆弱性评估[J].电力系统自动化,2012,36(19):11-16.LI Yong,LIU Junyong,LIU Xiaoyu,et al.Vulnerability assessment in power grid cascading failures based on entropy of power flow[J].Automation of Electric Power Systems,2012,36(19):11-16.
[19]李勇,刘俊勇,刘晓宇,等.基于潮流熵测度的连锁故障脆弱线路评估及其在四川主干电网中的应用[J].电力自动化设备,2013,33(10):40-46.LI Yong,LIU Junyong,LIU Xiaoyu,et al.Vulnerability assessment based on power flow entropy for lines in cascading failures and its application in Sichuan backbone power grid[J].Electric Power Automation Equipment,2013,33(10):40-46.
[20]曾珂,李华强,曾梦婕,等.考虑改进潮流转移熵的电力系统融冰预防控制[J].电网技术,2015,39(2):582-587.ZENG Ke,LIHuaqiang,ZENG Mengjie,etal.Powersystem ice-melting preventive controlconsidering improved transfer entropy of power flow[J].Power System Technology,2015,39(2):582-587.
[21]曹一家,王光增,曹丽华,等.基于潮流熵的复杂电网自组织临界态判断模型[J].电力系统自动化,2011,35(7):1-6.CAO Yijia,WANG Guangzeng,CAO Lihua,et al.An identification model for self-organized criticality of power grids based on power flow entropy[J].Automation of Electric Power Systems,2011,35(7):1-6.
[22]ETTORE B,ROBRETO N,FEIXue.Analysisofstructural vulnerabilities in powertransmission grids [J].International Journal of Critical Infrastructure Protection,2009,2(1):5-12.
[23]苟竞,刘俊勇,刘友波,等.基于能量熵测度的电力系统连锁故障风险辨识[J].电网技术,2013,37(10):2754-2761.GOU Jing,LIU Junyong,LIU Youbo,etal.Energy entropy measure based risk identification of power system cascading failures[J].Power System Technology,2013,37(10):2754-2761.
[24]李帅虎,曹一家,刘光晔,等.基于电压稳定在线监测指标的预防控制方法[J].中国电机工程学报,2015,35(18):4598-4606.LI Shuaihu,CAO Yijia,LIU Guangye,et al.Preventive control method ofelectric powersystem based on on-line voltage stability monitoring index[J].Proceedings of the CSEE,2015,35(18):4598-4606.
[25]李天云,陈昌雷,周博,等.奇异值分解和最小二乘支持向量机在电能质量扰动识别中的应用[J].中国电机工程学报,2008,28(34):124-128.LI Tianyun,CHEN Changlei,ZHOU Bo,et al.Application of SVD and LS-SVM in power quality disturbances classification[J].Proceedings of the CSEE,2008,28(34):124-128.
[26]冯治鸿,刘取,倪以信,等.多机电力系统电压静态稳定性分析——奇异值分解法[J].中国电机工程学报,1992,12(3):10-18.FENG Zhihong,LIU Qu,NI Yixin,et al.Analysis of steady-state voltage stability in multimachine power systems by singular value decomposition method[J].Proceedings of the CSEE,1992,12(3):10-18.
[27]陈敏,张步涵,段献忠,等.基于最小奇异值灵敏度的电压稳定薄弱节点研究[J].电网技术,2006,30(24):36-39.CHEN Min,ZHANG Buhan,DUAN Xianzhong,et al.Study on weak buses of voltage stability based on sensitivity of minimum singular value[J].Power System Technology,2006,30(24):36-39.
[28]徐慧明,毕天姝,黄少锋,等.基于WAMS的潮流转移识别算法[J].电力系统自动化,2006,30(14):14-19.XU Huiming,BI Tianshu,HUANG Shaofeng,et al.WAMS based flow transfer identification algorithm[J].Automation of Electric Power Systems,2006,30(14):14-19.
[29]闫常友,周孝信,康建东,等.潮流转移灵敏度以及安全评估指标研究[J].中国电机工程学报,2010,30(19):7-13.YAN Changyou,ZHOU Xiaoxin,KANG Jiandong,etal.Flow transferring sensitivity and security index analysis[J].Proceedings of the CSEE,2010,30(19):7-13.
[30]徐岩,吕彬,王增平.基于广域测量系统的潮流转移识别方法[J].中国电机工程学报,2013,33(28):154-160.XU Yan,LÜ Bin,WANG Zengping.A powerflow transfer identification scheme based on WAMS[J].Proceedings of the CSEE,2013,33(28):154-160.
[31]杨卫东,刘若晨,蔡景.属性权重确定方式及在衡量机型相似度中的应用[J].飞机设计,2014,34(5):58-61.YANG Weidong,LIU Ruochen,CAI Jing.The approach to weight determination and its application in measurement of similarity between aircraft[J].Aircraft Design,2014,34(5):58-61.
[32]CHEN J,THORP J S,DOBSON I.Cascading dynamics and mitigation assessmentin powersystem disturbances via a hidden failure model[J].InternationalJournalofElectrical Power&Energy Systems,2005,27(4):318-326.
[33]刘文颖,蔡万通,张宁,等.基于联合加权熵的电网自组织临界状态演化[J].中国电机工程学报,2015,35(6):1363-1370.LIU Wenying,CAI Wantong,ZHANG Ning,et al.Evolution of self-organizing of grid critical state based on united weighted entropy theory[J].Proceedings of the CSEE,2015,35(6):1363-1370.
[34]易俊,周孝信,肖逾男.电力系统自组织临界特性分析与仿真模型[J].电网技术,2008,32(3):7-12.YI Jun,ZHOU Xiaoxin,XIAO Yunan.Analysis on power system self-organized criticality and itssimulation model[J].Power System Technology,2008,32(3):7-12.
[35]王涛,王兴武,顾雪平,等.基于概率及结构重要度的电力系统事故链模型与仿真[J].电力自动化设备,2013,33(7):51-56.WANG Tao,WANG Xingwu,GU Xueping,et al.Power system fault chain model and simulation based on probability and structural importance[J].Electric Power Automation Equipment,2013,33(7):51-56.
[36]易俊,周孝信.考虑系统频率特性以及保护隐藏故障的电网连锁故障模型[J].电力系统自动化,2006,30(14):1-5.YI Jun,ZHOU Xiaoxin.Cascading failure model of power grids considering frequency response characteristics and hidden failures[J].Automation of Electric Power Systems,2006,30(14):1-5.
[37]陈得治,张伯明,方兴.节点注入功率模式对电压稳定裕度的影响[J].电网技术,2009,33(2):62-67.CHEN Dezhi,ZHANG Boming,FANG Xing.Effectofnodal injection power mode on voltage stability margin [J].Power System Technology,2009,33(2):62-67.

