高压直流接地极线路故障特性仿真及其故障测距新算法研究

程星星，张怿宁，王健，梁华彬

（1.华南理工大学，广东广州　510630；2.南方电网超高压输电公司检修试验中心研究生工作站，广东广州　510507）



高压直流接地极线路故障特性仿真及其故障测距新算法研究

程星星1，2，张怿宁2，王健1，梁华彬1

（1.华南理工大学，广东广州510630；2.南方电网超高压输电公司检修试验中心研究生工作站，广东广州510507）

摘要：高压直流输电系统可用大地构成输电回路，接地极系统运行方式复杂。建立了±500 kV直流输电系统仿真模型，分析了接地极线路故障时的运行特性，并针对接地极线路单线短路故障，提出了一种基于贝杰龙模型的接地极线路故障测距新方法。利用故障后首端电压和两出线电流推算沿线电压分布，根据故障点或极址点为全线电压最小值的特点构造故障测距函数，计算出故障距离。PSCAD/EMTDC仿真计算结果和工程实例表明，该算法可在接地极全线范围内实现故障定位，且具有较高精度。

关键词：高压直流输电；接地极线路；贝杰龙模型；故障测距；电压分布。

目前国内已投运的高压直流输电（HVDC）系统多为点对点直流输电系统，一般采用大地回线运行方式，其两端换流站中性母线经由接地极可靠接地。在实际工程中，接地极址一般选择远离换流站的偏僻地区，与换流站中性母线通过两平行架构的接地极线路连接，线路长度因极址地理位置而定，一般在几十以至上百公里。

高压直流系统在双极大地回线运行方式时，接地极线路流过双极不平衡电流，同时限制换流阀中性点电位，保护换流阀的安全；在单极大地回线运行方式时，接地极址入地电流为系统输电线路运行电流，此电流可达数千安，形成电流场会加速附近金属管道的腐蚀，现有部分直流系统运行规程不允许长时间采用该方式运行。但在直流工程投产初期或双极系统某一极发生故障导致单极闭锁时，为了发挥直流工程输电效益、减少因故障造成的输电损失，直流系统正常极往往采用单极大地回线运行方式，输送双极系统一半的功率，保障供受端交流系统的稳定性。因此，接地极系统对HVDC系统的经济高效运行具有重要意义[1-3]。

直流系统在单极大地回线运行方式下，接地极线路发生故障时，会危及故障点附近人畜安全，干扰通讯设施，甚至中断系统功率传送；在双极大地回线运行方式下，当系统某一极输电线路发生故障而需要单极闭锁操作时，若接地极线路运行状态不明确，系统无法转换为单极大地回线运行方式，从而导致双极闭锁。因此，接地极系统对HVDC系统的安全稳定运行具有重要意义，有必要开展接地极线路故障特性及测距研究，快速定位故障。

目前，针对接地极系统的研究主要集中在接地极线路故障时不平衡保护的动作策略上[4]，对接地极线路故障特性分析及故障定位的研究较少。文献[5]仅提出了一种辨别接地极线路近端金属性短路与断线故障的方法，未对接地极线路故障特性进行全面分析；文献[6-8]根据故障行波在接地极线路不均匀点折反射传播过程，在线路首端检测两次故障行波到达时间差来计算故障距离。但行波法对采样频率要求较高，且行波波头难于识别，在实际应用中易出现测距失败情况。文献[9-12]阐述了高压输电线路的故障特点，并将故障分析法用于直流输电线路的故障测距研究。本文以PSCAD/EMDTC为仿真平台，建立南方电网某±500 kV高流直流输电系统仿真模型，通过仿真，分析接地极线路发生各种故障时，电气量的变化特征及沿线分布情况，并采取接地极线路的贝杰龙模型，利用其首端电气量推算故障点或极址点电压，构造故障定位函数，计算故障距离。

1　HVDCT接地极系统模型

以南方电网某±500 kV双端直流输电工程为例，建立HVDCT接地极系统模型如图1所示。系统双极额定功率3 200 MW，可在双极大地、单极大地和单极金属回线方式下运行。图中C1、C2为接地极线路过电压吸收电容，可以吸收因遭受雷击或断线故障产生的能量；K1、K2为转换开关，用于系统不同运行方式的切换；M点为接地极线路电气量测量点，测量首端电压及其两分支出线电流；F为故障点，G为极址点；Rg为极址电阻。

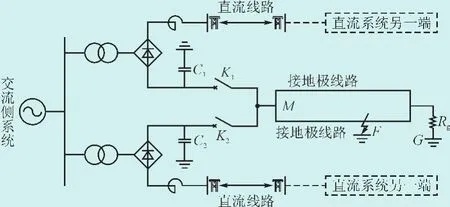
图1　HVDCT接地极系统模型Fig. 1 Simulation model for the HVDC electrode line

2　接地极线路故障特性分析

本文以HVDC系统单极大地回线运行方式为例，分析接地极线路发生单线接地、单线断线及相间短路故障时的电气量变化特征及沿线分布情况。

2.1接地故障

接地极系统正常运行时经极址处于良好接地。当发生单线接地故障时，接地极线路将处于两点接地状态，系统不平衡电流将在极址和故障点之间分布。当该故障为金属性接地故障时，即过渡电阻小于极址电阻，电流分布如图2所示，非故障线路l1上的电流i3将在极址N处分流，经极址G和故障点F流入大地；而故障线路l2的电流i2全部在故障点F处流入大地。此时故障点电压为全线电压最小值。当该故障为高阻接地故障时，即故障的过渡电阻大于极址电阻，电流分布如图3所示，故障线路l2电流i5将在故障点F处分流，经故障点F和极址点G流入大地，非故障线路l1上的电流i3全部在极址流入大地，此时极址处电压为全线电压最小值。

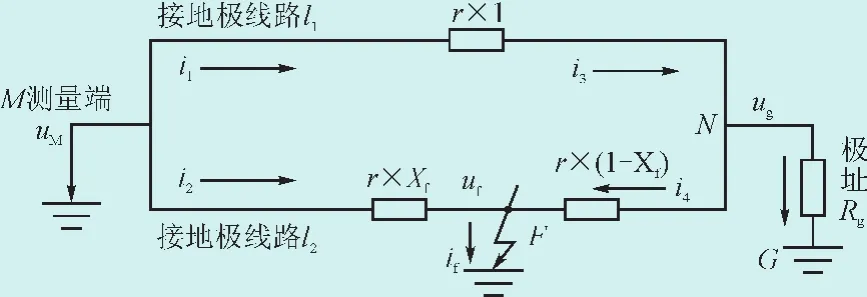
图2　金属性接地故障电流分布图Fig. 2 Current distribution of the metallic grounded fault

图3　高阻接地故障电流分布图Fig. 3 Current distribution of the high-impedancegrounded fault

图中xf为故障点到量测端的距离；uM为量测端电压；i1为线路l1的出线电流；i2为线路l2的出线电流；r为接地极线路单位长度电阻；l为接地极线路从量测端到极址点的距离。

2.2单线断线故障

当接地极线路发生单线断线故障时，故障线路l2上的电流i2为0，系统不平衡电流经非故障线路l1在极址点处流入大地，线路总阻抗增加，线路l1沿线电压升高。

2.3相间短路故障

接地极线路两条架空引出线的阻抗具有对称性，两线流过大小相等的直流电流。当发生相间短路时，不破坏2条出线的对称性，线路电气量特征及沿线分布基本不变。

3　接地极线路故障特性仿真

以PSCAD/EMTDC为仿真分析平台，基于南方电网某直流输电系统建立HVDC系统仿真模型（见图1）。HVDC系统以单极大地回线运行方式为例，额定输送功率1 600 MW，整流侧采取定电流控制，逆变侧采用定电压控制。

接地极线路选择贝杰龙参数模型，线路长度设为100 km，线路参数为r=0.021 5 Ω/km，l= 1.273 3 mH/km，c=1.04×10-8F/km，极址电阻Rg= 0.657 Ω。仿真采样频率为20 kHz，仿真时长12.25 s（其中直流仿真模型从启动到稳定运行需要10 s），设在12.1 s时发生故障，故障位置设定在整流侧接地极线路2距首端40 km处，故障类型为过渡电阻分别为5 Ω和0.1 Ω单线接地、单线断线故障及相间短路故障。故障电压和电流的仿真波形如图4～图7所示。

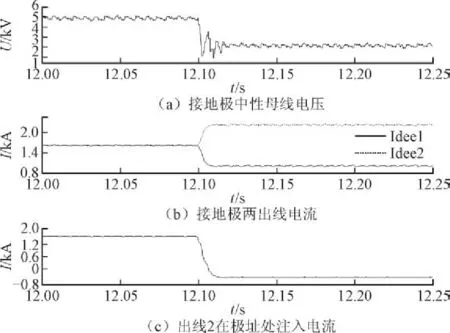
图4　金属性接地故障波形图Fig. 4 Waveform of the metallic grounding fault

为了判断故障线路电流在极址处的流向，监测接地极线路l2在极址处的注入电流I_gnd2。如图4所示，系统在单极大地回线运行方式下，接地极中性母线上的电压约为4.85 kV，且含有较为稳定的谐波分量，两出线电流大小相等，均为1.6 kA。发生金属性接地短路时，中性母线电压有较大幅度下降，故障线路电流大幅增加，非故障线路电流减小，故障线路在极址处的注入电流I_gnd2在故障后反向，由极址流向故障点，在接地极线路上形成局部回流。

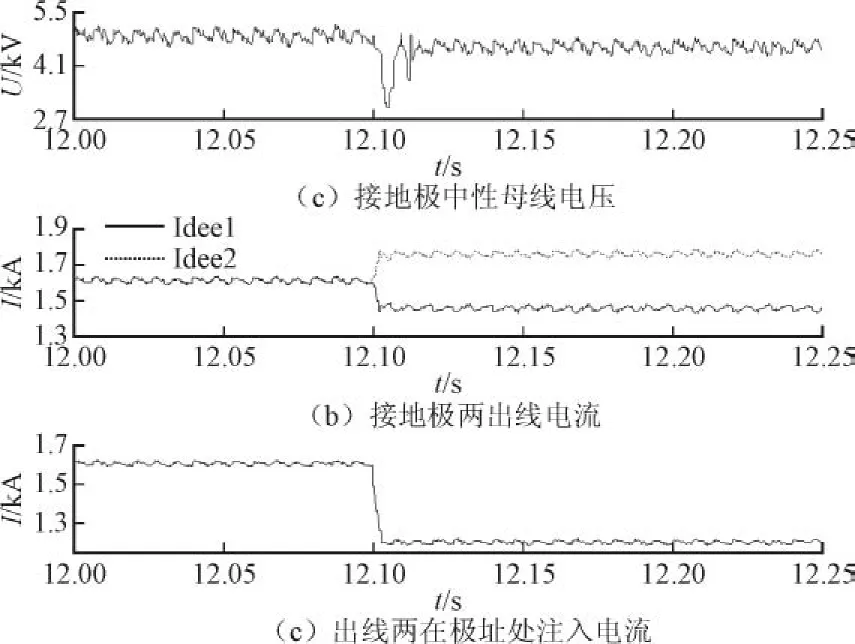
图5　高阻接地故障波形图Fig. 5 Waveform of the high-impedance-grounded fault

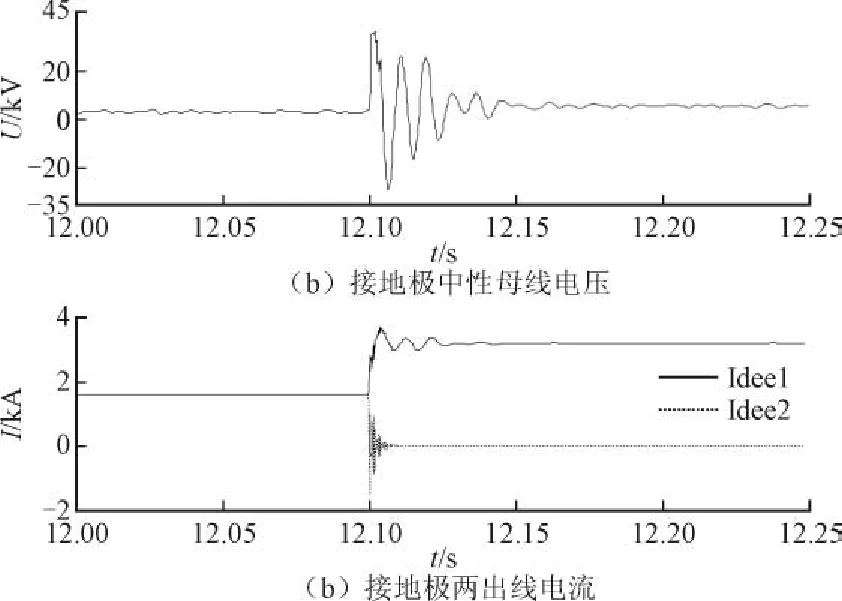
图6　单线断线故障波形图Fig. 6 Waveform of the single line break-down fault

图7　相间短路波形图Fig. 7 Waveform of the interphase short circuit

发生高阻接地故障后，如图5所示，接地极中性母线电压经过短暂波动后略有降低；故障线路电流增大，并在极址处入地电流I_gnd2大于0，流向不变；非故障线路电流减小，沿极址流入大地。

发生断线故障时，由图6可知，故障线路电流降为零，非故障线路电流经过短时波动稳定在3.2 kA，故障瞬间可在中性母线产生40 kV的冲击过电压，经过震荡衰减后稳定在8.6 kV，高于线路正常运行电压。

接地极双回线路发生相间短路后，由图7可见，中性母线电压和两出线电流基本没有变化，说明双回接地极线路发生对称性故障不影响线路电压分布与电流流向。

4　接地极线路故障测距新方法

双端故障测距方法需在极址处和换流站分别安装测距装置。由于极址通常位于偏远区域，无人值守，装置取电和维护极不便利，所以双端法故障测距在实际工程中难以应用。在换流站侧，接地极线路出线端都装有电压电流监测装置，具备单端法故障测距的条件。

本文根据线路的拓扑结构，建立接地极线路的贝杰龙模型；利用换流站测量端电气量，分别从不同方向计算沿线分布电压和分布电流；根据计算出来的沿线分布电压在故障点处时时相等的特性，构造故障定位函数。实际计算中，当接地极线路发生单线金属性接地故障时，如图2所示，故障点电压为全线电压最小值，从两个不同方向分别计算故障点电压，根据这两个故障点电压差值最小的特性构造测距函数；当发生高阻接地故障时，如图3所示，极址点电压为全线电压最小值，从两个不同方向分别计算极址点电压，根据这两个极址点电压差值最小的特性构造测距函数。求解测距函数即得故障距离。计算过程如下：

文献[13]推导了沿线任意时刻电压电流分布的计算公式，已知线路量测端电压和出线电流，依据接地极线路的贝杰龙等效模型，可计算沿线任意时刻的电压电流分布为

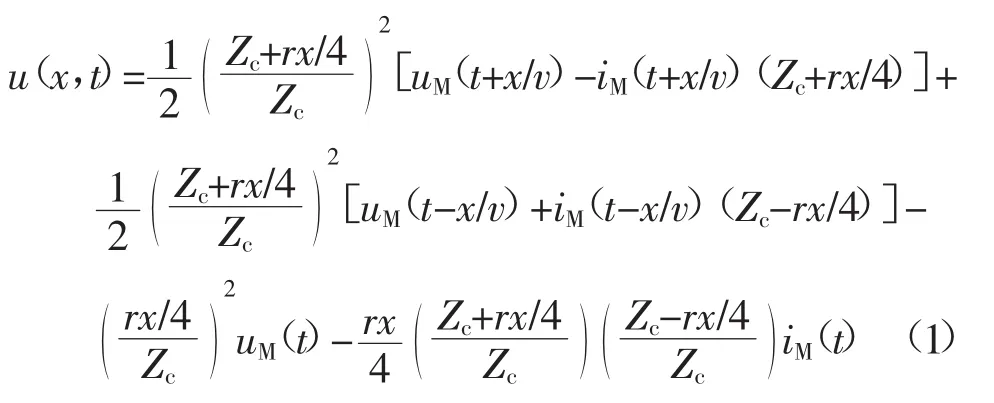
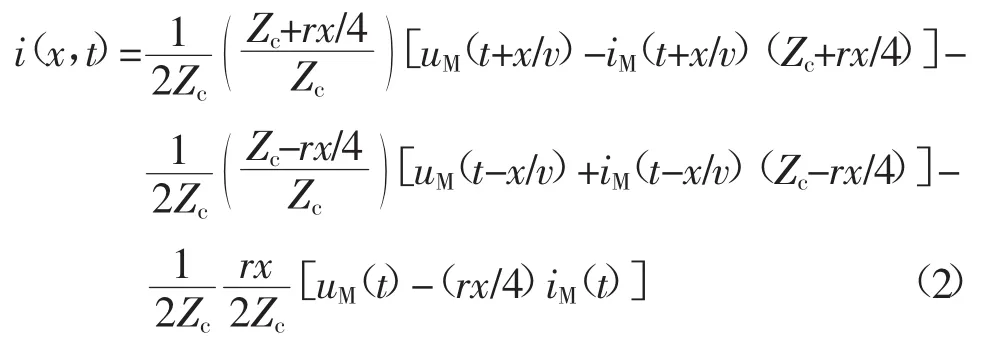
式中：r、Zc、v分别为线路电阻率、特征阻抗和波速度；uM（t）、iM（t）分别为t时刻M端的电压和电流；u（x，t）、i（x，t）分别为t时刻距M端x处的电压、电流。

1）对于金属性接地故障，故障点电压为全线电压最小值，线路电流分布如图2所示。利用故障后从不同方向计算出来的故障点电压时时相等的特点，列写测距函数的步骤如下：

①设故障距离为xf，根据贝杰龙电压电流沿线分布式（1）和式（2），由接地极线路测量端电压uM和故障线路l2的电流i2计算故障点电压uf1。

②根据贝杰龙电压电流沿线分布式（1）和式（2），由测量端电压uM和非故障线路l1的电流i1计算极址点电压ug和电流i3。

③由极址边界条件，故障线路l2末端电流i4=－ug/ Rg+i3，再由极址电压和故障线路l2极址侧电流i4计算故障点电压uf2。

④由故障点电压时时相等列写测距函数如下：

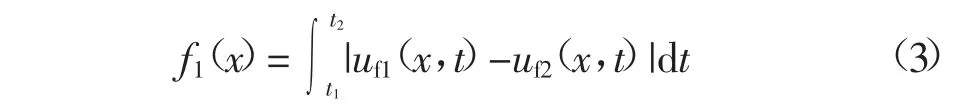
式中：t1、t2为数据冗余时间。由式（1）和式（2）可知，求得极址点特定时间电压值需2倍的全线传播时间，再由极址电气量计算全线电压分布也需2倍全线传播时间，所以利用首端电气量从不同方向推算线路单点电压需4倍全线传播时间，再加上式（3）冗余数据长度（3 ms左右），该算法所需数据长度tw为

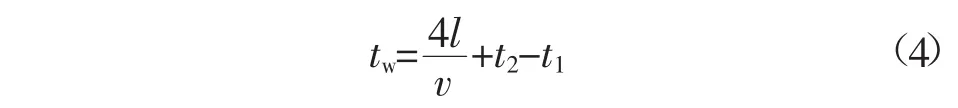
输电线路波速略低于光速，由式（4）可知，对于100 km长的接地极线路，5 ms左右的数据时窗满足测距要求。当t1、t2一定时，f1（x）为故障距离x的函数。

理论上，式（3）为0时所对应的x值即是故障距离。但在实际计算中，由于舍入误差和计算精度的影响，式（3）很难取到0，一般遍历求解其最小值时所对应x当作故障距离，即故障定位函数为

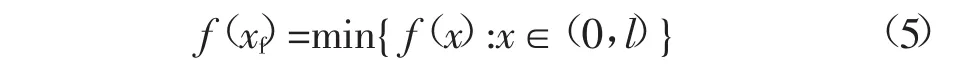
2）对于高阻接地故障，极址点电压为全线电压最小值，线路电流分布见图3，利用故障后从不同方向计算出来的极址点电压时时相等的特点，列写测距函数的步骤如下：

①根据贝杰龙电压电流沿线分布式（1）和式（2），由测量端电压uM和非故障线路l1的电流i1计算极址点电压ug1；

②设故障距离为xf，由测量端电压uM和故障线路l2的电流i2计算故障点电压uf和电流i5；

③设过渡电阻为Rf，根据故障边界条件，得故障点流向极址点的电流i6=uf/Rf－i5，Rf∈[Rmin，Rmax]，其中，Rmin、Rmax为过渡电阻的搜索范围，包含过渡电阻真实值；

④由故障点电压uf和电流i6计算极址点电压ug2；

⑤再根据极址点电压时时相等列写测距函数为

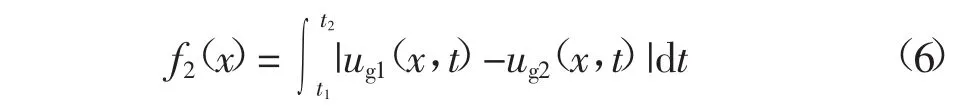
当数据时窗t1、t2一定时，f2（x）为故障距离x和过渡电阻Rf的函数。

由于接地过渡电阻未知，可通过二维搜索求解式（6）最小值时所对应的x即是故障距离，相应故障定位函数为

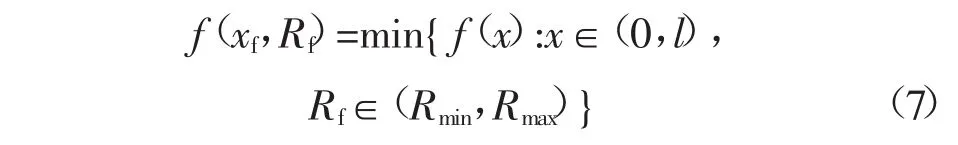
为了快速获取计算结果，本文采用粒子群算法求解测距函数（5）和（7）。粒子群算法首先将故障距离与过渡电阻初始化为一群随机粒子、测距函数作为适应度函数，然后通过个体极值和全局极值迭代更新找到最优解，即故障距离。

5　故障测距仿真及实例验证

5.1故障测距仿真

基于本文第3节仿真环境，本节仿真设置采样频率为100 kHz，利用12.245 s～12.250 s的数据时窗进行故障定位计算。在全线范围每隔10 km设置一个故障点，对金属性接地故障与高阻接地故障分别采用故障定位函数（5）和（7），计算测距结果如表1和表2所示。

由仿真结果可见：该算法对金属性接地故障和高阻接地故障最大测距误差均小于0.6 km，最大测距相对误差在0.6%范围内，具有较高的测距精度，并对全线范围内的接地故障均可实现精确定位。在实际工程中，接地极极址都经过良好接地，线路发生的接地故障时，过渡电阻一般大于极址电阻，在本算法中都可看作高阻接地故障处理。

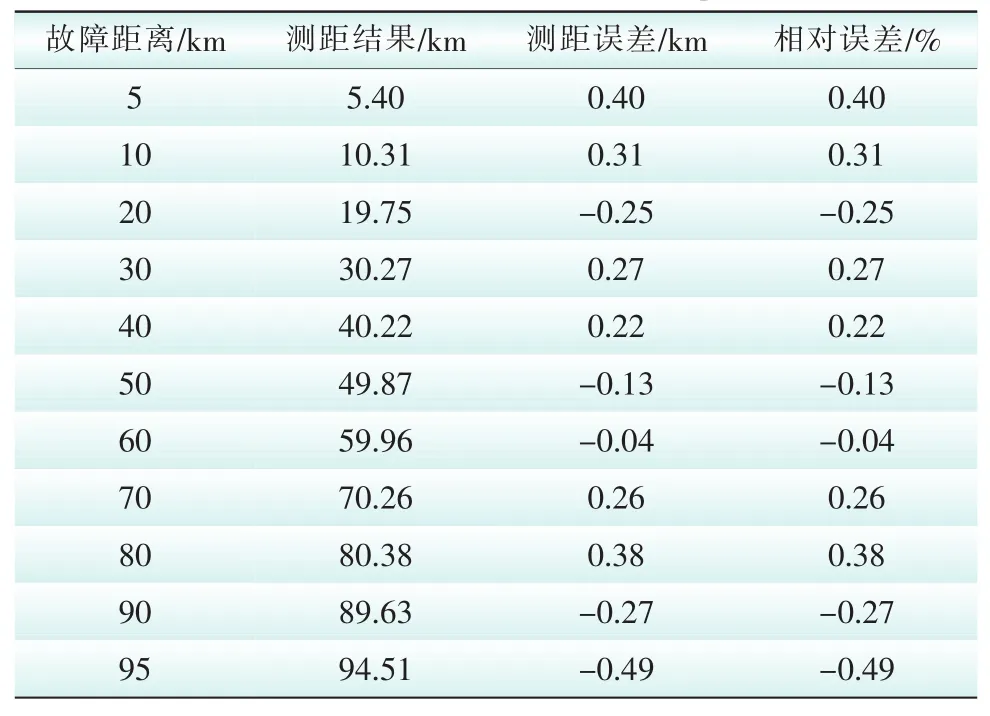
表1　金属性接地故障测距结果Tab. 1 Location result of the metallic grounded fault

表2　高阻接地故障测距结果Tab. 2 Location result of the high-impedancegrounded fault

5.2实例验证

2008年07月28日，某直流输电系统接地极线路发生单线接地故障，其换流站接地极线路不平衡保护（60EL）动作，启动极闭锁顺序，闭锁直流极，实际寻线发现故障点距换流站54.42 km。换流站采样录波数据频率为6.4 kHz，为了提高定位精度，对录波数据采取5倍插值，再利用本文接地极线路高阻故障的测距算法，测得故障距离为53.03 km。实例验证表明，本文测距算法满足实际工程中的精度需求。

6　结论

1）接地极线路故障时，具备以下特征：①发生金属性单线接地故障时，故障线路末端电流成逆向流动，并在故障点注入大地，此时，故障点为全线电压最低点；发生高阻接地故障时，故障线路电流会在故障点分流，并在极址点注入大地，此时，极址点为全线电压最低点。②发生单线断线故障时，故障瞬间将产生较高的暂态过电压，非故障线路沿线电压上升。③发生相间短路时，线路电压分布和电流流通形式基本无变化。

2）提出了一种基于贝杰龙模型的接地极线路故障测距新方法，可在全线范围内精确定位接地极单线接地故障。仿真试验结果验证了该方法的有效性和实用性。

参考文献

[1]赵畹君.高压直流输电工程技术[M].北京：中国电力出版社，2004.

[2]王明新，张强.直流输电系统接地极电流对交流电网的影响[J].电网技术，2005，29（3）：9-14. WANG Mingxin，ZHANG Qiang. Analysis on influence of ground electrode currentin HVDC on AC power network[J]. Power System Technology，2005，29（3）: 9-14（in Chinese）.

[3]王彪，王渝红，丁理杰，等.高压直流输电接地电极及相关问题综述[J].电力系统及其自动化学报，2012，24 （1）: 66-71. WANG Biao，WANG Yuhong，DING Lijie，et al. Summary of HVDC grounding electrode and related issues[J]. Proceedings of the CSU -EPSA，2012，24（1）: 66-71（in Chinese）.

[4]邵震，曹小拐，汲广.南方电网直流输电系统接地极不平衡保护动作策略分析[J].广东电力，2011，24（9）: 23-58. SHAO Zhen，CAO Xiaoguai，JI Guang. Analysis on action strategy of unbalance protection of earth electrode in DC transmission system of CSG[J]. Guangdong Electric Power，2011，24（9）: 23-58（in Chinese）.

[5]杨光，朱韬析，魏丽君，等.直流输电系统接地极线路故障研究[J].电力系统保护与控制，2009，37（21）: 45-49. YANG Guang，ZHU Taoxi，WEI Lijun，et al. Research on the faults of electrode line of HVDC transmission system in monopolar ground return operation[J]. Power System Protection and Control，2009，37（21）: 45-49（in Chinese）.

[6]何军娜，陈剑云，艾颖梅，等.电力系统行波测距方法及其发展[J].电力系统保护与控制，2014，42（24）: 148-153. HE Junna，CHEN Jianyun，AI Yingmei，et al. Fault location methods based on traveling wave theory for power system and its development[J]. Power System Protection and Control，2014，42（24）: 148-153（in Chinese）.

[7] AMMON J，HUANG H. Innovations in HVDC technology [R/OL]．[2007-12-01]. http://www.Photonicpower.com.

[8]王彩芝，姜映辉，王俊江，等.基于PSCAD/EMTDC的HVDC接地极线路故障仿真[J].中国电力，2014，47（2）: 69-72. WANG Caizhi，JIANG Yinghui，WANG Junjian. PSCAD/ EMTDC-Based simulation research on HVDC grounding line fault[J]. Electric Power，2014，47（2）: 69-72（in Chinese）.

[9]宋国兵，蔡新雷，高淑萍，等.高压直流输电线路故障定位研究综述[J].电力系统保护与控制，2012，40（5）: 133-136. SONG Guobing，CAI Xinlei，GAO Shuping，et al. Suvey of fault location research for HVDC transmission lines[J]. Power System Protection and Control，2012，40（5）: 133-137（in Chinese）.

[10]李强，王银乐，高淑萍，等.高压输电线路的故障测距方法[J].电力系统保护与控制，2009，37（23）: 192-197. LI Qiang，WANG Yinle，GAO shuping，et al. Fault location methods for high voltage power transmission lines[J]. Power System Protection and Control，2009，37（23）: 192-197（in Chinese）.

[11]李小叶，李永丽，张烁，等.基于混合智能算法的直流输电线路故障测距方法[J].电力系统保护与控制，2009，37（23）: 192-197. LI Xiaoye，LI Yongli，ZHANG Shuo，et al. Fault location method based on hybrid intelligent algorithm for HVDC transmission line[J]. Power System Protection and Control，2014，42（10）: 108-113（in Chinese）.

[12]刘家军，闫泊，姚李孝，等.同杆平行双回线的故障测距综述[J].电网与清洁能源，2010，26（11）: 75-81. LIU Jiajun，YAN Bo，YAO Lixiao，et al. A survey of fault location for double-circuit parallel transmission lines on the same pole[J]. Power System and Clean Energy，2010，26（11）: 75-81（in Chinese）.

[13]宋国兵，索南加乐，许庆强，等.基于双回线环流的时域法故障定位[J].中国电机工程学报，2004，24（3）: 24-29. SONG Guobing，SUONNA Jiale，XU Qingqanig，et al. A novel time-domain algorithm for Iocation fault on parallel transmission lines by circuit [J]. Proceeding of the CSEE，

2004，24（3）: 24-29（in Chinese）.

程星星（1990—），男，硕士研究生，主要研究方向为电力系统故障测距；

张怿宁（1973—），男，教授级高级工程师，工学博士，主要从事超高压交、直流输电系统自动化、故障测距、继电保护与控制的研究、仿真和检修工作；

王健（1965—），女，副教授，主要研究方向为电力市场；

梁华彬（1991—），男，硕士研究生，主要研究方向为电力市场需求响应。

（编辑李沈）

HVDC Grounding Electrode Line Fault Simulation and Its New Fault Location Algorithm Research

CHENG Xingxing1，2，ZHANG Yining2，WANG Jian1，LIANG Huabin1
（1. South China University of Technology，Guangzhou 510630，Guangdong，China；2. Graduate Workstation of CSG EHV M&T Center，Guangzhou 510507，Guangdong，China）

ABSTRACT：With earth taken as part of the HVDC system loop，the grounding electrode system is connected to ground effectively，the operation mode of the system is different from normal HVDC lines. A±500 kV HVDC system model is established in this paper by using PSCAD/EMTDC simulation platform，based on which the fault operation characteristic of grounding electrode line is simulated and analyzed，and a fault location method based on the Bergeron line model aimed at single line grounded short circuit is also put forward in this paper. The head-end voltage and current of two outlets after fault are used to calculate the voltage distribution along line. According to the characteristics that the fault or electrode point is the minimum voltage along line，the fault location function is established to calculate the fault distance. The simulation result and project instances indicate that the fault of the grounding electrode line can be located accurately with the proposed method. KEY WORDS：HVDC；grounding electrode line；Bergeron line model；fault location；voltage distribution

作者简介：

收稿日期：2015-11-06。

文章编号：1674- 3814（2016）03- 0105- 06

中图分类号：TM721.1

文献标志码：A