变压器磁路饱和与二次侧无功电压控制可行性

曹芸，田沛川，王珂，霍明飞，蒋蕾，王承民，宋枭楠

（1.上海交通大学电子信息与电气工程学院，上海　220240；2.大连地区装备修理检修室，辽宁大连　116041；3.国网白城市城郊供电公司，吉林白城　137100；4.国网辽宁省电力有限公司，辽宁沈阳　110006）



变压器磁路饱和与二次侧无功电压控制可行性

曹芸1，田沛川1，王珂2，霍明飞3，蒋蕾4，王承民1，宋枭楠1

（1.上海交通大学电子信息与电气工程学院，上海220240；2.大连地区装备修理检修室，辽宁大连116041；3.国网白城市城郊供电公司，吉林白城137100；4.国网辽宁省电力有限公司，辽宁沈阳110006）

摘要：主要阐述了变压器磁路饱和的基本原理。以小斜率模型作为磁化曲线模型，分析变压器经直流磁饱和控制后，其无功电压随饱和程度的变化情况。对变压器磁路饱和现象进行分析，利用直流电流控制铁芯饱和程度使变压器在传输功率的同时具备连续可调的无功补偿能力。以240 MV·A/500 kV单相变压器为算例进行仿真分析，结果表明，加入直流励磁后，变压器可作为感性无功源对电网进行无功补偿，调节线路节点电压。

关键词：变压器；磁饱和；无功补偿；电压控制

Project Supported by National High-tech Research and Development Program（863 Program）（2015AA050101）.

随着国民经济的不断发展，电力系统可靠性成为越来越关注的问题。与此同时，随着电网规模不断扩大和网络结构的日益复杂，由负荷波动带来的不稳定因素日益加剧。因此，电网的无功需求无论在配置方面还是运行模式方面都发生了很大变化，需采取多种手段保证无功平衡。

作为动态无功源之一的磁控电抗器，由于其具有可靠性高、控制简单、电流波形失真度低等优点而得到普遍关注[1-2]。随着磁控电抗器的日益成熟和广泛使用，其低维护成本、低谐波含量的优势日益显露[3-5]。磁控电抗器在使用中多和变压器安装在一起，而变压器和磁控电抗器在结构上的相似性带来的一个重要启示是：能否对变压器的无功补偿能力进行挖掘，使变压器同时具备功率传输能力和无功调节能力。从电机学角度看，磁控电抗器可以看成二次侧开路的变压器；而在电网中，变压器的等值电路模型又往往是一个纯电抗器。所以，可以从理论上把二者结合起来，将磁控电抗器无功补偿的原理[6-10]应用于变压器中，使变压器既能正常传输功率，又能实现对电网进行可调感性无功补偿[11-12]。

目前，对于变压器磁饱和方面的研究主要针对直流偏磁效应，但着重点都是要抑制这种现象，以免引起大量的谐波以及无功损耗等。然而，若能有效地对高次谐波进行过滤和抑制，就可以对变压器的磁饱和特性加以利用，使变压器作为感性无功源，可以有效抑制线路因容性负荷而造成的电压升高，也可以与并联电容器组一起组成连续可调的（从感性到容性）的无功补偿。本文将重点研究变压器的磁饱和特性以及励磁基波电流与无功电压特性，高次谐波的过滤和抑制问题在此不作讨论。

1　变压器的磁路饱和

变压器在正常工作时，铁芯始终处于不饱和状态，其等效磁阻非常大，从而产生的励磁电流非常小，几乎可以忽略。而变压器的无功补偿量取决于励磁电流的大小，因此，若不采取措施改变铁芯的饱和程度，那么变压器就几乎不具备无功补偿的能力。为了改变变压器铁芯的磁饱和程度，在变压器的一次侧增加额外的绕组作为控制绕组。

使变压器磁饱和有2种方式，加入直流激磁或者交流激磁。两者的区别在于加入直流激磁不会改变铁芯中磁感应强度的波形，只是增加了磁感应强度的直流分量，变压器二次侧电压不会受到影响；而加入交流激磁则会影响二次侧电压，使其发生畸变。因此，在控制绕组上施加一个大小可调节的直流电源，改变直流电源的大小就可以改变铁芯的磁饱和程度。

如图1所示，引入磁势、磁阻以及磁通的概念，可以画出与之相对应的等效磁路图，如图2所示。变压器一次侧分别绕有匝数为N1的交流工作绕组以及匝数为Nk的直流控制绕组，变压器二次侧绕组匝数为N2。铁芯柱截面积为S，长度为l。将变压器一次侧工作绕组接至交流电源Umcos ωt，控制绕组接到直流电压源Ik。

图1　变压器的磁路饱和Fig. 1 Magnetic saturation of the transformer

当直流绕组开路时，变压器只进行功率的传输，其铁芯处于不饱和状态，励磁电流非常小，无功补偿量可以忽略不计；当二次侧开路时，可控磁饱和变压器不进行功率传输，只进行无功补偿，其无功补偿量由直流控制侧绕组中的电流决定；当二次侧接入负载并且直流侧同时施加一定的电压时，可控磁饱和变压器就可以实现在传输功率的同时，通过调节直流控制绕组电压的大小来改变磁路饱和程度，进行可调无功补偿。

图2　等效磁路图Fig. 2 Equivalent magnetic circuit diagram

假设铁芯磁场强度为H，磁通量为φ，左侧铁芯磁阻为R1，右侧铁芯磁阻为R2；一次侧输入电流为i1，二次侧输出电流为i2，控制绕组输入电流为Ik；左侧磁势为F1，右侧磁势为F2，连接左右两柱的铁芯磁阻为R3。

由于左右两侧铁芯柱长度相同、截面积相同，由公式Rm=可知R1=R2=R。因此，可以根据等效磁路图列出方程：

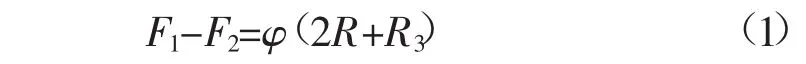
对于变压器来说，铁芯柱的长度要比仅用作导通磁场的磁轭部分要长得多，因此，可以忽略R3，又由公式F=NI可得：

将式（2）、式（3）代入式（1），得：

由式φR=Hl，可得磁路基本方程：

令铁芯中的磁密为B，则基本电路方程为：

当变压器二次侧空载时，由空载电流建立变压器的主磁通，此空载电流也就是励磁电流im。当变压器二次侧带上负载的时候，一次侧的电流i1可以分解为2部分，励磁分量im与负载分量。励磁分量用于建立变压器的主磁通，负载分量建立用于平衡二次侧电流的磁势。因此，引入励磁电流后im可以将式（5）简化为：

当变压器的一次侧铁芯饱和程度通过控制绕组上施加的直流电源改变后，其等效阻抗发生了变化，励磁电流随之改变，变压器的无功补偿能力取决于励磁电流ief的基波分量。

2　饱和程度与二次侧无功电压变化关系

下面计算中饱和程度用饱和角β来定义，如图3所示。

图3　磁化曲线与饱和角定义Fig. 3 Magnetization curve and saturated angle definition

根据图3，可得磁化曲线方程为：

谐波电流随饱和角变化方程为：

式中：β为饱和角；I1（2n+1）m为各次谐波；Bs为铁芯饱和磁通；N1一次侧线圈匝数；l0为一次侧磁路长度。令n=0，可以得到补偿量随饱和角的变化情况：

不考虑变压器本身的容量限制时，其无功补偿容量近似为：

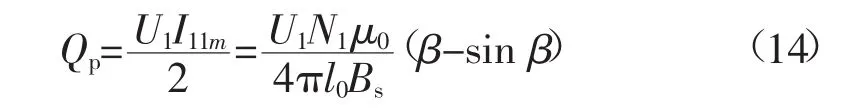
考虑到变压器本身的容量限制，其所能提供的最大无功补偿量应当是变压器容量减去负荷的量。极端情况是变压器二次侧空载，则变压器除了损耗外，全部容量用于无功补偿。设变压器容量为SN，二次侧负荷为Sτ，那么最大无功补偿量Qpm=SN－Sτ。

设变压器二次侧负荷为Sτ=Pτ+jQτ，电源电势为Es，线路等效阻抗为Zs=Rs+jXs，系统短路容量Ssc=，变压器二次侧电压为U2，变比为K。则：

由于电压幅值的变化，因此为方便分析，忽略电压的横向分量ΔUX，电压变化量为：

式中：φsc=arctan

一般情况下，电网电阻比电抗小得多，忽略负荷有功变化造成的电压波动。因此，可以将式（17）简化为：

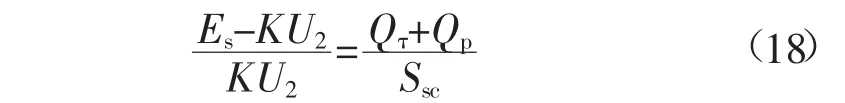
因此，可以得到电压的关系式：

由于Qτ+QpSsc，将式（13）展开后保留线性项得：

将式（13）代入式（20）即可得到二次侧电压特性：

结合变压器无功补偿量的限制，在负荷一定的情况下，二次侧电压的调节范围是

3　饱和角与直流控制电流关系

根据磁化曲线的模型，当磁感应强度不超过Bs时，近似认为此时的磁场强度为0。这是因为此时磁导率过大，忽略了微弱的磁场强度。

由图3可知，当ωt=π时，磁感应强度的峰值为：

对应的磁场强度的峰值为：

将ωt=π代入式（10）、式（11）可得：

将式（23）代入式（24）得：

由于此时对于1柱的左半柱来说处于饱和状态，故式（25）同时成立，则有：

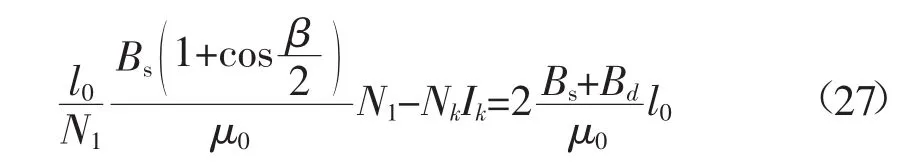
由图3可得：

联立式（27）和式（28）可得Ik与β的关系：

4　仿真分析

以240 MV·A/500 kV的单相变压器为例，进行仿真分析。其各项参数为Um=449 086 V，N1=508匝，N2=32匝，l=4.225 m，S=4.225 m2。令控制绕组匝数为300匝，根据式（10）分别绘制出控制电流Ik=0、Ik=1 A时的励磁电流波形，如图4所示。

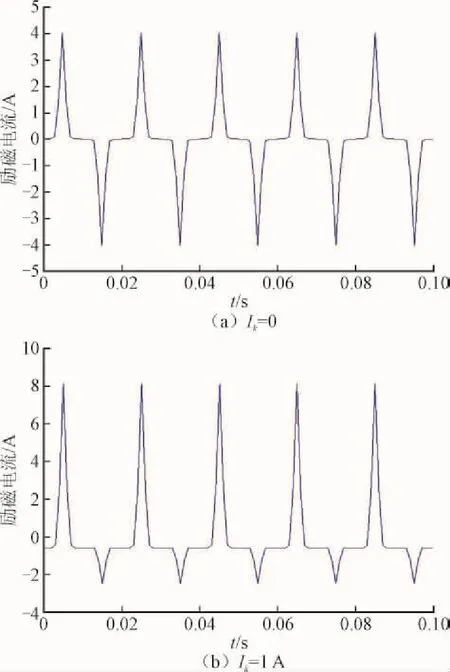
图4　不同控制电流下励磁电流波形Fig. 4 Excitation current waveform under different current control

由于变压器通常工作在铁芯磁化曲线的膝点四周，此时铁芯已接近或略微饱和了，当加入直流电源后，铁芯进入饱和工作区域，因此励磁电流出现畸变。

励磁基波电流的幅值为：

励磁基波电流幅值与饱和角的关系曲线如图5所示。

图5　励磁电流随饱和角变化曲线Fig. 5 The excitation current curve changing with saturated angle

500 kV输电线路参数R0=0.026 25 Ω/km，X0=0.284 Ω/km，线路长度为100 km，假设线路末端带容性负荷，即Ql=－20 MV·A，则变压器二次侧电压为：

图6所示为二次侧电压与控制电流的关系曲线，可以看出变压器二次侧电压随着控制电流的增大而减小。因此可以得出结论：变压器作为感性无功源可以有效抑制线路因容性负荷而造成的电压升高，也可以与并联电容器组一起组成连续可调的（从感性到容性）的无功补偿。

图6　二次侧电压与控制电流的关系Fig. 6 Relationship between the secondary voltage and current control

5　结语

本文阐述了变压器磁饱和的基本原理，对变压器磁饱和后的无功补偿能力进行了分析，基于小斜率函数磁化曲线模型分析了变压器加入直流励磁后，变压器无功电压随饱和角的变化特性。以240 MV·A/ 500 kV单相变压器为例，加入直流励磁，进行了仿真分析，证明加入直流励磁后变压器可作为感性无功源对电网进行无功补偿，调节线路的节点电压。

参考文献

[1]周腊吾，朱英浩，周之光.特高压可控并联电抗器的调节范围[J].电工技术学报，2006，21（12）: 116-119. ZHOU Lawu，ZHU Yinghao，ZHOU Zhiguang. Regulating range of UHV controlled shunt reactor[J]. Transactions of China Electrotechnical Society，2006，21（12）: 116-119 （in Chinese）.

[2]段绍米，刘海鹏.基于磁控电抗器的风电场无功补偿[J].电气时代，2012（12）: 68-70. DUAN Shaomi，LIU Haipeng. Reactive power compensation of wind farm based on magnetically controlled reactor[J]. Electric Age，2012（12）: 68-70（in Chinese）.

[3]周勤勇，郭强，卜广全，等.可控电抗器在我国超/特高压电网中的应用[J].中国电机工程学报，2007，27（7）: 1-6. ZHOU Qinyong，GUO Qiang，BU Guangquan，et al. Application of controllable reactors in China’s power grid at extra and ultra voltage level[J]. Proceedings of the CSEE，2007，27（7）: 1-6（in Chinese）.

[4]田翠华，陈柏超.磁控电抗器在750 kV系统中的应用[J].电工技术学报，2005，20（1）: 31-37. TIAN Cuihua，CHEN Bochao. Application of magnetically controlled reactor in 750 kV power system[J]. Transactions of China Electrotechnical Society，2005，20（1）: 31-37 （in Chinese）.

[5]余梦泽，陈柏超，曹志煌，等. 110 kV并联可控电抗器及其应用[J].电力系统自动化，2008，32（3）: 87-91. YU Mengze，CHEN Bochao，CAO Zhihuang，et al. 110 kV parallel controllable reactor and its application[J]. Automation of Electric Power Systems，2008，32（3）: 87-91（in Chinese）.

[6] BELYAEV A N，SMOLOVIK S V. Steady-state and transient stability of 500 kV long-distance AC transmission lines with magnetically controlled shunt reactors[C]. IEEE Power Tech Conference，Russia，2005.

[7]王轩，邓占锋，于坤山，等.超高压磁控式并联电抗器稳态特性[J].中国电机工程学报，2008，28（33）: 104-109. WANG Xuan，DENG Zhanfeng，YU Kunshan，et al. Steady-state characteristics of extra-high voltage magnetically controlled shunt reactor[J]. Proceedings of the CSEE，2008，28（33）: 104-109（in Chinese）.

[8]陈柏超，田翠花，梁柏华，等.单相可控电抗器的一种谐波抑制原理及实现[J].中国电机工程学报，2002，22 （3）: 63-67. CHEN Bochao，TIAN Cuihua，LIANG Bohua，et al. Principle and implementation of a harmonic depression approach for single-phase controlled saturable reactor[J]. Proceedings of the CSEE，2002，22（3）: 63-67（in Chinese）.

[9]陈柏超.新型可控饱和电抗器理论及应用[M].武汉:武汉水利电力大学出版社，1999.

[10]田铭兴，励庆孚，王曙鸿.磁饱和式可控电抗器的等效物理模型及其数学模型[J].电工技术学报，2002（8）: 18-21. TIAN Minxing，LI Qingfu，WANG Shuhong. An equivalent physical model and a mathematical model of the controlled

saturable reactor[J]. Transactions of China Electrotechnical Society，2002（8）: 18-21（in Chinese）.

[11] SAKIS MELIOPOULOS A P. Effects of DC ground electrode on converter transformers[J]. IEEE Trans on Power Delivery，1994，19（1）：194-205.

[12]梅文哲，赵建，范小辉，等.变压器调压区均压环的设计与优化[J].江苏电机工程，2014，33（4）：48-51. MEI Wenzhe，ZHAO Jian，FAN Xiaohui，et al. Design and optimization of transform voltage adjusting zone grading ring[J]. Jiangsu Electrical Engineering，2014，33（4）：48-51（in Chinese）.

曹芸（1990—），女，硕士研究生，主要研究方向电力系统无功补偿、低电压治理和变压器磁饱和控制。

（编辑董小兵）

Transformer Magnetic Saturation and Controllability of the Secondary Side Reactive Power and Voltage

CAO Yun1，TIAN Peichuan1，WANG Ke2，HUO Mingfei3，JIANG Lei4，WANG Chengmin1，SONG Xiaonan1
（1. Department of Electronic Information and Electrical Engineering，Shanghai Jiaotong University，Shanghai 220240，China；2. Dalian Equipment Repair Maintenance Room，Dalian 116041，Liaoning，China；3. State Grid Baicheng City Suburb Power Supply Company，Baicheng 137100，Jilin，China；4. State Grid Liaoning Electric Power Co.，Ltd.，Shenyang 110006，Liaoning，China）

ABSTRACT：This paper mainly expounds the basic principles of magnetic saturation of the transformer. With the small slope model as the magnetization curve model，the paper analyzes changes of reactive power with saturation degree after the transformer has had the DC saturation control. The paper also examines the magnetic saturation phenomenon of the transformer，and by using DC power to control the transformer core saturation level，the transformer is made able not only to output the transmit active power but also to conduct continually reactive power compensation. Finally a 240 MV·A/500 kV single-phase transformer is taken as an example for simulation analysis and the result shows the transformer can be used as a source of inductive reactive power for reactive power compensation to regulate the node voltage circuit after joining DC excitation.

KEY WORDS：transformer；magnetic saturation；reactive power compensation；voltage control

作者简介：

收稿日期：2015-04-17。

基金项目：国家高技术研究发展计划（863计划）资助（2015A A050101）。

文章编号：1674- 3814（2016）03- 0013- 05

中图分类号：TM412

文献标志码：A