基于优化的LS- SVR的继电保护设备故障率预测模型
邓旭阳,陈志光,林燕贞,龚庆武
(1.广东电网有限责任公司电力调度控制中心,广东广州 510600;2.武汉大学电气工程学院,湖北武汉 430072)
基于优化的LS- SVR的继电保护设备故障率预测模型
邓旭阳1,陈志光1,林燕贞2,龚庆武2
(1.广东电网有限责任公司电力调度控制中心,广东广州510600;2.武汉大学电气工程学院,湖北武汉430072)
摘要:电力系统的互联运行对继电保护设备提出更高的要求,而继电保护设备的安全稳定运行与故障率息息相关。为了解决标准粒子群(SPSO)陷入局部最优的问题,加入高斯扰动操作,提出了高斯扰动的标准粒子群算法(GDSPSO),并在优化过程改变传统学习因子是定值的缺陷,引入学习因子随着迭代次数变化的表达式,提高算法的搜索能力,更好地优化最小二乘支持向量机(LS-SVR)的学习参数,建立预测模型,并作误差分析。最后以某一地区相同型号,相同运行环境的24台继电保护设备为例,说明GDSPSO相比较其他3种算法而言,寻优速度快,稳定性好,计算耗时短,利用GDSPSO优化得到的学习参数建立的预测模型,预测效果好,预测精度高。
关键词:继电保护设备;故障率预测;LS-SVR;标准粒子群算法;高斯扰动标准粒子群算法;学习因子
Project Supported by National Science and Technology Support Program(2013BAA02B01)。
随着电力的大规模生产,对于电力设备的安全性要求越来越高,电力设备的故障诊断和寿命预测越来越重要[1-2]。故障率预测是寿命预测的根本,本文针对继电保护设备的故障率预测展开说明。
文献[3]规定,“微机继电保护装置的使用年限一般不低于12 a,对于运行不稳定、工作环境恶劣的微机继电保护装置,可根据运行情况适当缩短使用年限”。实际运行中继电保护装置一般在10~12 a之间退出运行,但退出运行时装置状况多为良好,装置寿命尚未结束,会造成资源浪费。目前对继电保护装置寿命相关研究较少,现有的文献一般都是先对继电保护设备进行状态评估,然后在状态评估的基础上利用健康指数模型求解相应的剩余寿命;或者偏重研究装置的可靠性与最佳检修周期关系等:这些研究有利于设备全寿命周期成本的降低和运行可靠性提高,但对装置寿命未展开研究[4-6]。同时,为保证结果的精确度,需要大量的样本作为支撑。但实际情况是由于继电保护装置种类和型号极多,且每一种装置的元器件数量多,元器件寿命相关参数难以收集,使得以上的方法具有很大的局限性。文献[7]加速老化不失为一种可行性方法,但加速模型及相关参数难以核定,以此预测寿命误差较大。因此建立一套能够在小样本条件下进行继电保护设备寿命的预测模型,是对继电保护系统可靠性正确分析和客观评价的前提。
支持向量回归机法是目前针对小样本估计和预测学习的最佳理论,已被认为是人工神经网络法的替代算法[8-9]。但是由于支持向量机需要求解一个凸二次规划问题,计算较为复杂,因此本文引入最小二乘的支持向量机,将不等式约束转化为等式约束,把计算简单化。在最小二乘支持向量机参数的求解上目前常用的方法有网格搜索方法、遗传算法和粒子群算法[10]。粒子群算法(PSO)由于其计算耗时少并且稳定好,被广泛应用在参数寻优方面。但是PSO很容易陷入早熟收敛,为了解决这个难题,文献[11]提出采用标准粒子群算法(SPSO)来进行参数优化。针对SPSO进化后期收敛速度慢和收敛精度低的缺点,文献[12]提出一种改进的非线性递减算法来改变SPSO惯性权重的表达式,该算法能够较好地调整全局与局部搜索能力之间的平衡。文献[13]提出一种基于高斯扰动的粒子群优化算法,实例证明收敛速度和寻优精度都优于其他算法。
本文提出一种基于最小二乘支持向量机的小样本条件下,分别采用遗传算法、粒子群算法以及改进的粒子群算法,分析某地区的相同型号、运行环境相同的24台继电保护设备,利用前6年的故障率历史数据,作为训练样本,建立预测模型,采用第7年故障率作为测试样本,并和相应的实际值相比较,计算相应的误差,选取最佳的预测模型。
1 支持向量回归机
在统计学习理论上发展起来的支持向量机是一种具有坚实基础的机器学习算法,它建立在VC维理论和结构风险最小化原理之上,通过核函数的方法,把线性不可分的模式输入映射到一个高维Hilbert特征空间,利用线性可分技术进行求解[14]。由于其核心算法本质上是一个凸二次规划问题,所以能保证找到的极值解就是最优解。
支持向量回归机预测方法是一种基于历史数据的预测方法,它利用数据之间的相关性,寻找历史数据内在的函数规律,进而对未来数据进行预测。可见,基于支持向量回归机继电保护设备故障率预测总体分为构建预测模型和使用预测模型进行预测两大步骤,其中构建支持向量机预测模型是预测过程的重点,它是利用给定的数据,选择适当的参数和核函数,求解得到决策函数的全过程。本文研究了几种常用的智能算法进行支持向量机预测模型参数优化,通过具体实例分析了不同方法的预测效果。
文献[14]对支持向量机做了详细的叙述,这里就不在赘述。支持向量机模型不仅考虑了训练样本的复杂性,而且还考虑了数据曲线的拟合性,并具有很好的泛化能力。但由于它需要求解一个凸二次规划问题,计算较为复杂,且需要计算和存储核函数矩阵,因此当样本点较多时,需要占用很大的存储空间。针对这种情况,Suykens、Vandewalle在SVR的基础上提出了最小二乘支持向量机(LS-SVR)[15]。LS-SVR采用二次损失函数,并将不等式约束转化为等式约束,这样支持向量机求解过程的二次寻优问题就可转化成线性KKT(Karush-Kuhn-Tucker)方程组求解,极大地降低了求解复杂性,在保证精度的同时大大降低了计算复杂性,加快了求解速度[16]。
对于训练样本集(xi,yi),其中i=1,2,…,l;i∈Rn,xi为第i个输入变量;yi为xi对应输出变量;l为训练样本数目。支持向量机的目的就是寻非线性映射,将输入值x映射到一个高维特征空间,在这个空间内构造线性回归方程[17]
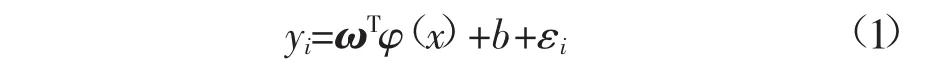
式中:ω为权向量,拥有与核空间相同的维度;b为偏置常数;φ(x)为映射函数;εi为损失函数。
损失函数ε[12]的含义是:样本点处的真实值与预测值的差的绝对值不超过ε时,认为此样本点的预测值等于真实值,即

最小二乘支持向量机优化目标采用损失函数εi的平方项。根据结构风险最小化原理,目标函数和约束函数分别为
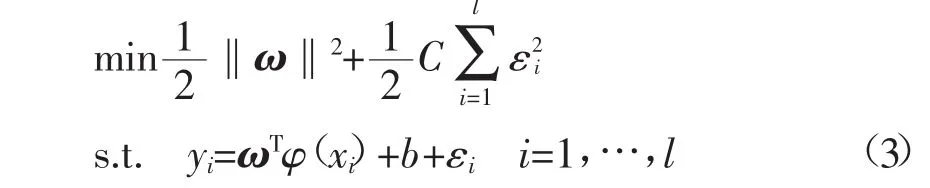
式中:C为正规化参数,用于控制样本噪声对模型的影响。其中第一项体现LS-SVR最大间隔算法特征,令拟合函数更加平坦;第二项用于减少训练误差,用正规化参数C控制对错分样本惩罚的程度,实现在错分样本比例与算法复杂度之间的折衷,提高了LS-SVR的推广能力。
为解上述优化问题,构造对偶空间的拉格朗日函数:
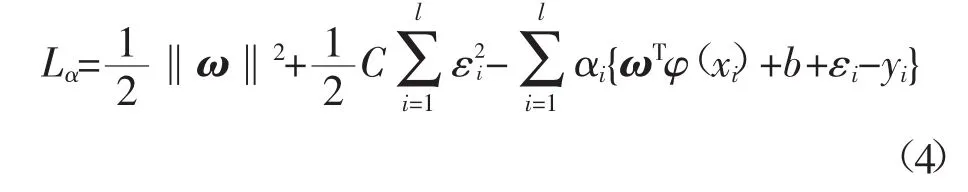
式中:αi为拉格朗日乘子。根据KKT条件,置各变量偏导数为0:
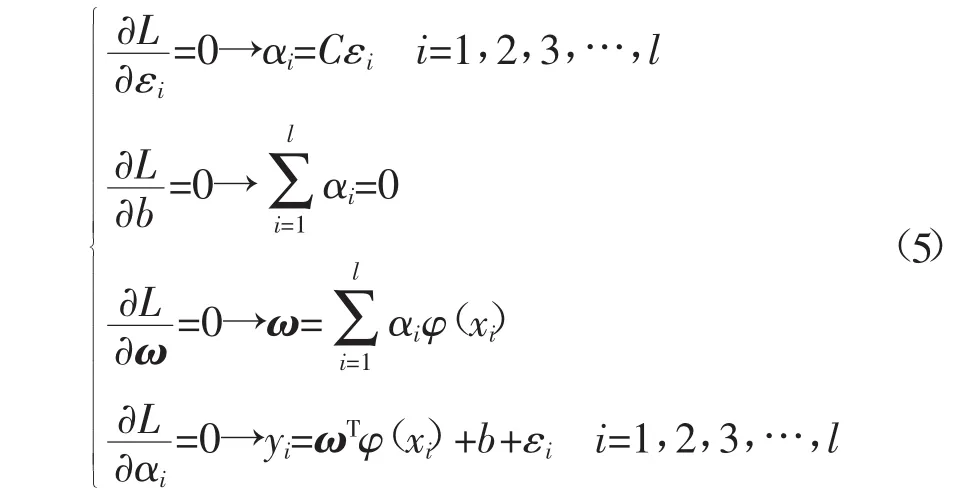
联立式(4)、式(5)消去上式中的ω、ε,可得以下线性方程组:
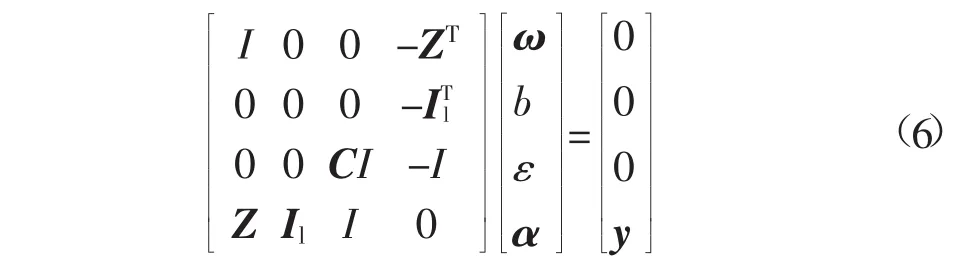
式中:y=[y1,y2,…,yl],Il=[1,1,…,1],
α=[α1,α2,…,αl],Z=[φ(x1),φ(x2),…,φ(xl)],
利用Mercer条件
Ω=φ(xi)Tφ(xj)=K(xi,xj),i,j=1,2,…,l消去无关项,所得方程组只与b和α有关,即:

根据式(7)得到b和α的数值后,利用核函数便可确定回归函数:
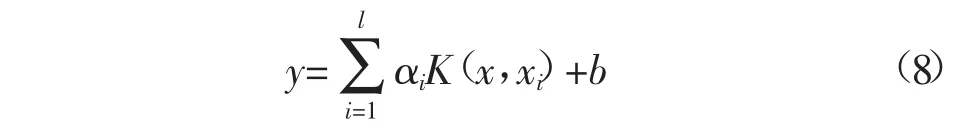
关于核函数的选取,文献[14]指出支持向量机有3种核函数,但是本文选择高斯径向基核函数(RBF)。由图1分析可知,RBF核函数对于一定范围内的数据有很好的插值能力,这个范围由参数σ决定,这种性质称为RBF核函数的局部性。本文研究继电保护设备的故障率预测是根据局部历史数据进行的,这些数据与设备周围的环境以及检修人员的工作情况密切相关,带有一定的波动性,局部性比较强,因此本文选取RBF核函数用于继电保护设备故障率预测。
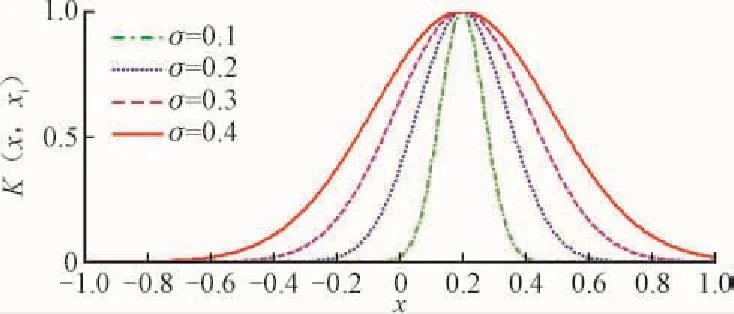
图1 RBF核函数Fig. 1 RBF kernel function
计算式为

式中:σ为核参数。
2 最小二乘支持向量机参数的确定
由上述对LS-SVR原理的论述可知,LS-SVR中需要确定的参数包括模型参数和核参数两类,即为正规化参数C、损失函数ε,以及核参数σ。传统的经验法和留一法在寻优上没有比较规范的评定方法。为此,一种较为规范而可行的算法评定方法,即k-折交叉验证法(k-CV),被提出。比较成熟的算法有:网格搜索算法、基于遗传算法或其他启发式算法的参数寻优方法等。但是网格搜索法需要先定位好区间,浪费时间;遗传算法存在随机操作并且寻优过程复杂,收敛速度慢比较难收敛;粒子群算法(PSO)收敛速度快,而且比较精确。因此本文基于k-CV原理,采用改进的标准粒子群算法(SPSO)对参数进行优化。
2.1标准粒子群算法
标准粒子群算法对随机粒子群进行迭代运算,寻找最优解。粒子通过跟踪2个“极值”来更新自己的位置以及速度,一个是粒子本身的最优解pbest,另一个是整个种群目前的最优解gbest[18]。
PSO的数学表达为:假设在一个m维空间中,粒子的数量为n,粒子集为X=(x1,…,xi,…,xn)在空间中第i个粒子的位置表示为xi=(xi,1,xi,2,…,xi,m),速度表示为vi=(vi,1,vi,2,…,vi,m),粒子的速度和位置更新方程:
式中:vi,j(t)和xi,j(t)为粒子i在第t次迭代中第j维的速度和位置;c1和c2为学习因子;pbesti,j(t)为粒子i在第t次迭代个体极值的第j维;gbestg,j(t)为粒子群体在第t次迭代个体全部极值的第j维;ε1,ε2是在[0,1]区间上均与分布的随机数;w(t)为当前迭代次数下的惯性权重。
惯性权重主要是为了平衡粒子全局和局部的搜索能力,w比较大时,有比较强的全局搜索能力,w比较小时,有较强的局部搜索能力。为了使计算过程简单一点,本文选择线性递减权重粒子群算法来计算w(t),w(t)的迭代公式如下[19]:

式中:wmax为最大惯性权重;wmin为最小惯性权重;tmax为最大迭代步数;t为当前迭代步数。通常情况下,取wmin=0.4,wmax=0.9。
分析式(10)可以发现,式子是由3部分组成的,第一部分代表粒子当前的速度,反应粒子当前的状态;第二项反映了粒子对自身的学习,使粒子有足够强的全局搜索能力,避免局部最优;第三部分反映了粒子间的协作,体现了粒子间的信息共享,粒子位置更新如图2所示。
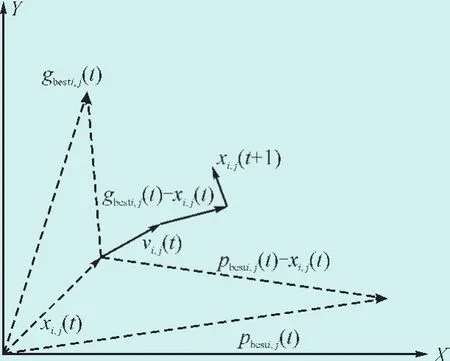
图2 粒子位置更新示意图Fig. 2 Particle position update diagram
2.2加入高斯扰动的标准粒子群算法
通过对SPSO的分析可以知道,到迭代后期,粒子的多样性下降,陷入局部最优,因此本文对SPSO进行改进,引入高斯扰动操作促使算法跳出局部最优,进入解空间的其他区域进行搜索,以达到提高计算精度的要求。常用的扰动操作主要由以下3种策略:1)在全局最优位置增加扰动操作;2)在平均最好位置加入扰动;3)在全局最优位置和平均最好位置同时加入扰动。文献[20]分别研究了以上3种策略,通过标准测试函数的仿真表明,在扰动加在平均最好位置取得的效果最好,因此将高斯扰动项加入到速度迭代公式中有
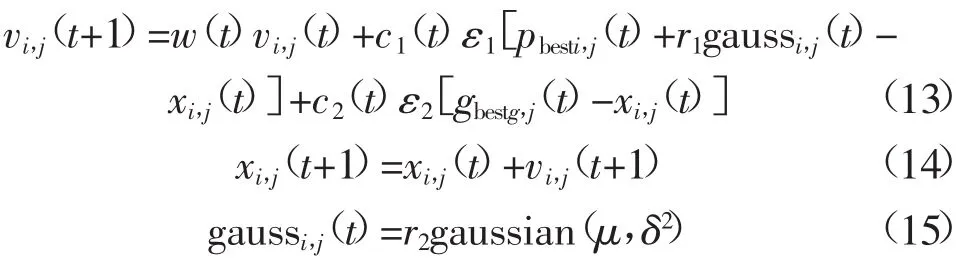
式中:gaussi,j(t)为粒子i在迭代次数为t时产生的高斯扰动;μ为均值;δ2为方差;r1,r2是在[0,1]区间上均匀分布的随机数;gaussian表示期望为μ,方差为δ2的高斯分布;其他参数的定义同式(10)、式(11)。
由式(15)可知,高斯扰动和均值μ以及方差δ2有关,因此本文选取μ=0,δ2=|pbesti,j(t)|。
学习因子c1(t)和c2(t)也称为加速因子,主要表示例子的自我学习能力和向群体中其他优秀粒子学习的能力,以便于快速向历史最优位置以及全局的最优位置运动。c1(t)采用线性递减的表达式,c2(t)采用单调递增的表达式。在迭代初期,c1(t)比较大,保证粒子在局部范围内寻优,有利于算法的收敛,随着迭代的进行,较大的c2(t)有利于跳出局部最优点,便于全局搜索。c1(t)和c2(t)的表达式为

式中:c1(t)为从初值c1i线性减小到终值c1f;c2(t)为从初值c2i线性增加到终值c2f。
综上所述,GDSPSO的算法步骤为:
1)粒子的初始化,设置相关参数。
2)评价和计算每个粒子的适应度函数值。
3)计算每个粒子的个体最优位置和群体最优位置,并计算每次迭代时粒子个体历史最优位置的高斯扰动值。
4)按照式(13)、式(14)对粒子的速度和位置进行更新,并计算粒子新的适应度值。
5)若算法满足终止条件,则停止迭代,输出全局最优粒子位置及其适应度值,否则继续循环步骤2)。
2.3基于GDSPSO的最小二乘支持向量机参数寻优
2.3.1数据预处理
数据的预处理主要是数据的归一化处理,一方面可以降低原始数据成分之间由于量值差异对故障率预测造成的影响,另一方面可以提高算法的泛化性。将原始数据规整到[0,1]范围内,其函数映射为:
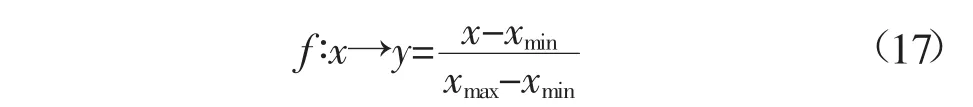
2.3.2适应度函数的选取
本文采用均方误差(MSE)作为适应度函数[21],表达式为

式中:yi为训练输出值;yi为实际值;G为适应度函数,
G越小表示选择的一组学习参数效果相对较好。
2.3.3参数寻优
构造和求解最优化问题的过程,需要使用样本数据,即继电保护设备故障率历史数据值,通过样本的训练,确定优化问题的最优解,得到支持向量机参数的最优解。
2.3.4建立预测模型
寻找合适的(C,σ,ε)之后,建立最小二乘支持向量回归机的模型,对继电保护设备的故障率进行预测。
2.3.5预测结果分析
分析预测误差是研究预测方法和预测模型的重要手段。本文采用平均相对百分比误差(eMRE),均方根误差(eRMSE)和相对百分比误差(eRE)作为衡量指标,表达式分别为

式中:yi为预测值;yi为真实值;n为预测的数据个数。
综上所述,基于高斯扰动的粒子群算法优化最小二乘支持向量机做继电保护设备故障预测的步骤如图3所示。
2.4预测算法的选择
为减小单步预测带来的误差,本文采用多步预测方法。常用的多步预测方法有2种,即滚动多步预测法和直接多步预测法[22]。假设现有训练样本数据m个,即m个真实值,以提前k步预测为例,滚动预测法使用单步预测方法,使用第1到m个样本数据点计算得到第m+1点预测值,而后将第2到m个数据点和m+1点的预测值作为新的训练样本,使用单步预测方法得到第m+2点预测值,依此迭代k次,实现提前k步预测[23]。直接预测法在使用训练样本求解模型时,以第i+k个样本点作为第i样本点的训练目标,得到多步预测模型,而后使用这种模型直接计算得到第m+1到m+k点的预测值。使用滚动预测法进行多步预测的缺陷在于,前一时刻预测值的误差会累积到下一时刻预测值中,使得预测误差随预测步数不断增大,预测效果不断变差,而直接预测法直接多步预测,不需要依靠单步预测的结果,是直接利用历史观察值进行预测。根据文献[22-24]里的实例证明,直接多步预测往往能预测得到和单步迭代预测一样,甚至更好的结果,因此本文使用直接多步预测来预测继电保护设备的故障率。
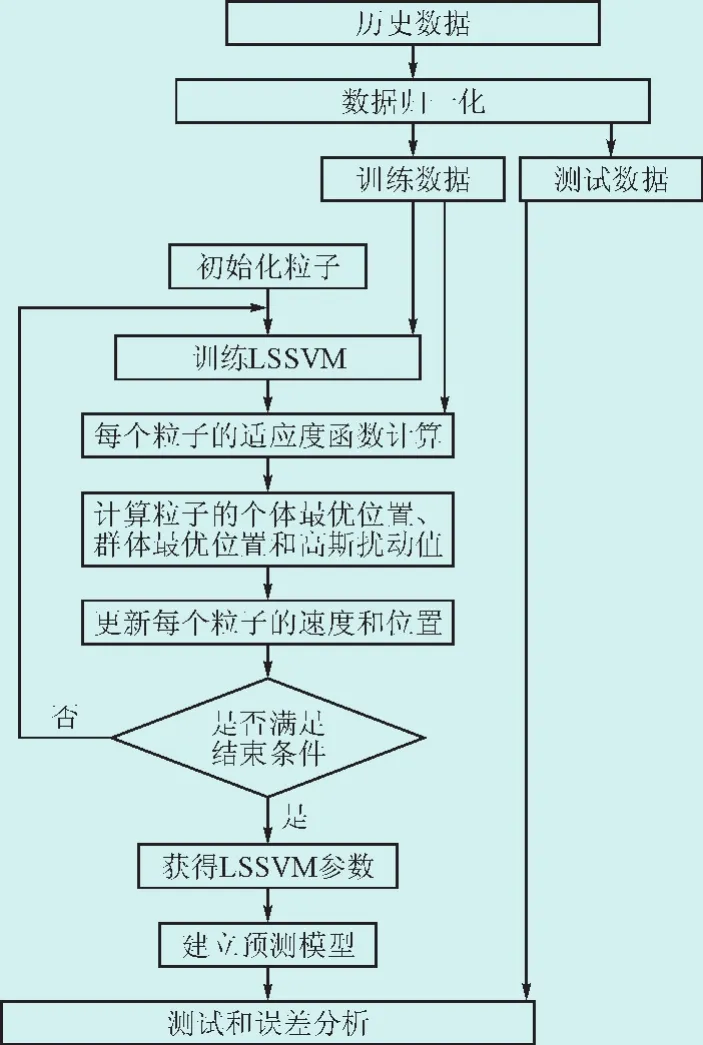
图3 最小二乘支持向量回归机的预测步骤Fig. 3 Prediction step of support vector regression
3 算例分析
3.1研究对象与参数
本文以某地区相同型号,运行环境相同的24台继电保护设备的前6年的历史数据为训练样本,供建立预测模型使用,取第7年的故障率作为测试样本,用于检验预测效果。样本数据是在每年同一时间进行采样。
本文采用提前6步的预测方法,对继电保护设备的故障率进行直接多步预测。分别采用PSO、GA、SPSO和GDSPSO进行预测,并且通过预测值和实际值之间的相对误差以及回归误差来比较算法的优越性。学习参数的搜索范围如下:C∈[0,1 000],ε∈[0.001,1],σ∈[0.01,10]。
3.2算法性能分析
4种算法的群体规模均取为N=20,最大迭代次数取为M=200。GA采用轮盘选择算子,均匀交叉和基本位变异,交叉验证折数k=5;PSO,SPSO的学习因子选为2,惯性权重选为ω=1,交叉验证折数k=5,GDSPSO的学习因子初值以及终值的取值分别为c1i= 2.5,c1f=0.5;c2i=0.5,c2f=2.5。
在实际编程计算中,同种算法在对同一数据进行多次计算时,得出的最佳参数和计算结果不尽相同。这种现象在理论上可以解释为,启发式优化算法大量使用随机操作,每次的迭代过程和迭代结果可能是不同的,因此对每种算法分别独立运行50次。
表1是对4种算法鲁棒性进行分析。分别对4种算法进行50次计算,记录适应度函数数值,找到4种算法的适应度函数数值最优解和最差解。分析表1可知,GA的寻优能力差,计算耗时长,寻找最优解和最差值之间的时间偏差为16.61%,且每次寻优过程波动剧烈;最优适应度函数数值为0.020 781,最优值和最差值之间的偏差为0.183 4,相比较其他3种算法而言,鲁棒性最差,算法不够稳定。相对而言,PSO比较稳定,适应度函数值的最优和最差值的偏差较GA下降了9.84%,计算平均耗时减小了65.288 s,但是寻优速度较SPSO慢;SPSO算法的训练结果较GA和PSO有了较大提升,适应度偏差分别下降了9.89%和0.05%;平均计算耗时仅为15.99 s,最小时间耗时仅为16.205 s,是4种算法中最短的,这验证了SPSO鲁棒性好和计算耗时短的优点;GDSPSO适应度函数的最优值和最差值之间的偏差为0.064 6,相比较其他3种算法而言,GDSPSO的训练效果最好,鲁棒性强。但是由于在计算过程需要加入扰动,因此计算时间相对SPSO长点,平均耗时为17.723 s,增加了1.733 s。综上所述,GDSPSO继承了SPOS寻优速度快、算法稳定性好的特点。

表1 4种算法的训练结果Tab. 1 Training results of four algorithms
图4—图7表示4种算法在寻优过程中,最佳适应度以及平均适应度随着进化代数变化曲线。

图4 GA搜索算法寻优图Fig. 4 GA search algorithm
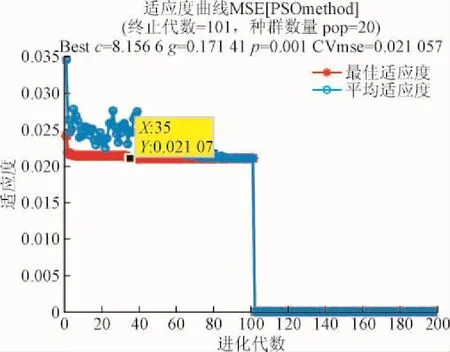
图5 PSO搜索算法寻优图Fig. 5 PSO search algorithm
分析图4—图7可知,GDSPSO算法的拟合效果很好,并且收敛速度很快,在第2代就收敛到适应度函数最优解;GA在第56代左右才收敛到适应度函数的最优解;PSO在35代左右才收敛到适应度函数的最优解;SPSO在24代左右收敛到适应度函数的最优解。因此,在拟合度上,SPSO有明显的优势。
表2是4种算法在最优适应度函数值下的学习参数。不同算法下得到的正规化参数差别很大,但都在合理的取值范围内。

图6 SPSO搜索算法寻优图Fig. 6 SPSO search algorithm

图7 GDSPSO搜索算法寻优图Fig. 7 GDSPSO search algorithm
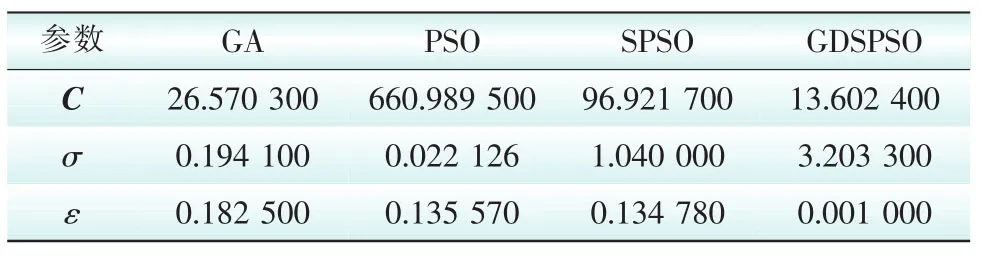
表2 4种算法得到的最优学习参数Tab. 2 The optimal learning parameters of four algorithms
文献[20]指出,当核参数σ较小时,为获得较好的拟合效果,需要较多的支持向量机个数,计算耗时长,当σ较大时,需要的支持向量机个数少,因此计算耗时短。分析表2可以知道,SPSO以及GDSPSO 的σ较大,因此计算耗时短。
综上所述,GDSPSO继承了PSO鲁棒性能好,计算耗时短,并且高斯扰动的引入提升了算法的寻优能力,计算精度、计算速度和算法的稳定性都远远优于GA和PSO算法。因此,GDSPSO可以为LSSVR学习参数的选择提供更精确的解。
3.3 4种算法预测结果分析
采用表2的最优学习参数构建LS-SVR预测模型,对第7年继电保护设备的故障率进行预测,预测结果表3所示,对应的预测图如图8所示。

表3 4种模型对故障率的预测Tab. 3 Four models for fault prediction
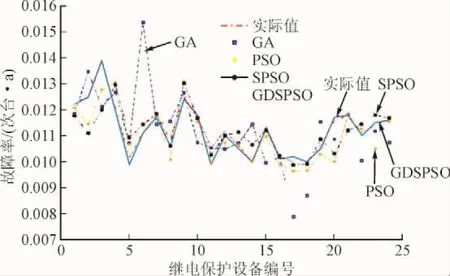
图8 4种模型下的继电保护设备故障率预测Fig. 8 Four models of fault prediction for relay protection equipment
分析图8可知,采用GA-LSSVR模型得到的故障率波动大,不平稳性大,随机性成分高,但是采用GDSPSO-LSSVR得到的故障率预测曲线和实际值曲线很接近,预测效果好。
表4和表5分别是回归误差和预测误差的分析,由表4分析可知,GDSPSO-LSSVR相对误差为10.94%,比GA-LSSVR,PSO-LSSVR,SPSO-LSSVR相比降低了3.408%,1.186%,1.181%;故障率的均方根误差为0.001 200 2(次/台·a),明显小于其他3种算法,这主要是因为通过GDSPSO算法得到的学习参数建立的预测模型精确度以及泛化能力都得到提高。

表4 4种模型的预测误差分析Tab. 4 Analysis of prediction error of four models

表5 4种模型的回归误差分析Tab. 5 Regression error analysis of four models
图9是分别采用4种模型对24台继电保护设备预测结果的相对误差分析(eRE),表5是24台继电保护设备的相对误差分布情况。

图9 4种模型预测的相对误差分析Fig. 9 Relative error analysis of four algorithms
表6是对图9的另一种表达方法,主要是为了说明预测的相对误差。由表6以及图9可知,由GDSPSOLSSVR模型得到的预测故障率相对误差小,位于(0~5%)的预测数目占了绝大多数,有17个,采用GALSSVR模型得到的相对误差分析只有19个在合理范围内(0~10%),其他都在10%以外,SPSO-LSSVR以及PSO-LSSVR模型的预测效果相当。综上所述,采用GDSPSO算法优化LSSVR的学习参数,鲁棒性好,预测误差小,模型的稳定性强。

表6 4种模型预测的相对误差的分布情况分析Tab. 6 The distribution of relative errors of four algorithms
4 结语
本文讨论了基于最小二乘支持向量回归机预测算法,在已知历史数据的基础上,采用4种算法求解LS-SVR的学习参数,并在此基础上建立预测模型,对预测值和实际值做了相应的比较,得出GDSPSO相比其他3种算法寻优速度快,算法稳定性好,提高故障率预测的准确性,为后续工作的开展提供理论依据。
参考文献
[1]薛斌,谢宏杰,唐卓贞.继电保护状态检修辅助管理系统的研究与应用[J].电网与清洁能源,2015(4): 20-24. XUE Bin,XIE Hongjie,TANG Zhuozhen. Research and application of relay protection predictive diagnosis maintenance assistant management system[J]. Power System and Clean Energy,2015(4): 20-24(in Chinese).
[2]王睿琛,薛安成,毕天姝,等.继电保护装置时变失效率估算及其区域性差异分析[J].电力系统自动化,2012,36(5):11-15.WANG Ruichen,XUE Ancheng,BI Tianshu,et al.Timevarying failure rate estimation of relay protection devices and their regional differences analysis[J].Automation of Electric Power Systems,2012,36(5): 11-15(in Chinese).
[3] DL/T 587-2007微机继电保护装置运行管理规程[S].2008.
[4]李永丽,李致中,杨维.继电保护装置可靠性及其最佳检修周期的研究[D].济南:山东大学,2010.
[5]陈飞.继电保护系统可靠性评估模型研究[D].重庆:重庆大学,2009.
[6]柳运华,樊恩红.电力系统继电保护可靠性研究[J].科技资讯,2011(22): 142-142.LIU Yunhua,FAN Enhong.Study on reliability of relay protection for power system[J].Technology Information,2011(22): 142-142(in Chinese).
[7]李亦非,邹战明,祁邦彦,等.基于寿命应力模型的电能表加速寿命试验研究[J].现代电子技术,2011,34(20): 167-170. LI Yifei,ZOU Zhanming,QI Bangyan,et al. Research on intelligent electricity meter based on“Lifestress”model[J]. Modern Electronics Technique,2011,34(20): 167-170 (in Chinese).
[8] MUKHERJEE S,OSUNA E,GIROSI F. Nonlinear prediction of chaotic time series using support vector machines[C]// Proceedings of IEEE NNSP’97,Amelia Island: 1997: 511-520.
[9]何旭,姜宪国,张沛超,等.基于SVM的小样本条件下继电保护可靠性参数估计[J].电网技术,2015,39(5): 1432-1437. HE Xu,JIANG Xianguo,ZHANG Peichao,et al. SVM based parameter estimation of relay protection reliability with small samples[J]. Power System Technology,2015,39(5): 1432-1437(in Chinese).
[10]浦星材,沈晓风,张清扬,等.基于偏最小二乘法的支持向量机短期负荷预测[J].电网与清洁能源,2011(10): 32-35,42. PU Xingcai,SHEN Xiaofeng,ZHANG Qingyang,et al. Short term load forecasting based on partial least squares support vector machine[J]. Power System and Clean Energy,2011(10): 32-35,42(in Chinese).
[11]张真真,李智录,王科,等.最小二乘支持向量机在大坝渗流监测中的应用[J].电网与水力发电进展,2008 (2): 65-68. ZHANG Zhenzhen,LI Zhilu,WANG Ke,et al. Short term load forecasting based on partial least squares support vector machine[J]. Advances of Power Grid and Hydropower,2008(2): 65-68(in Chinese).
[12] EBERHART R C,SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization[C]// In IEEE Transactions on Evolutionary Computation,Indianapolis,2000:84-88.
[13]薛建辉,洪刚,贾嵘.基于PSO优化LS-SVM的异步电动机振动故障诊断[J].电网与清洁能源,2010(1): 83-87. XUE Jianhui,Honggang,JIA Rong. Introduction motor vibration fault diagnosis by LS -SVM based on PSO[J]. Power System and Clean Energy,2010(1): 83-87(in Chinese).
[14]李娇.支持向量机参数优化研究[D].武汉:华中师范大学,2011.
[15]龚松建,袁宇浩,王莉,等.基于PSO优化LS-SVM的短期风速预测[J].可再生能源,2011,29(2): 22-27. GONG Songjian,YUAN Yuhao,WANG Li,et al. The LS-SVM short-term wind speed prediction based on PSO optimized[J]. Renewable Energy,2011,29(2): 22-27(in Chinese).
[16]丁龙,郝虎在,吕玉祥,等.基于支持向量机回归法的绝缘子污闪电压预测研究[J].电瓷避雷器,2014(1): 23-25. DING Long,HAO Huzai,LÜ Yuxiang,et al. Research on the prediction of the pollution flashover voltage of insulator based on support vector machine regression[J]. Insulators and Surge Arresters,2014(1): 23-25(in Chinese).
[17]程声烽,程小华,杨露.基于改进粒子群算法的小波神经网络在变压器故障诊断中的应用[J].电力系统保护与控制,2014,42(19): 37-42. CHENG Shengfeng,CHENG Xiaohua,YANG Lu. Application of wavelet neural network with improved particle swarm optimization algorithm in power transformer fault diagnosis[J]. Power System Protection and Control,2014,42(19): 37-42(in Chinese).
[18]张瑾,潘必超.基于支持向量机高压静电场闪络信号的模糊识别[J].电网与清洁能源,2015,31(8): 1-5. ZHANG Jin,PAN Bichao. Fuzzy recognition of flashover signal in high voltage electrostatic field based on support vector machine[J]. Power System and Clean Energy,2015,31(8): 1-5(in Chinese).
[19]张锋利,陈文献,贾海英.支持向量机和BP神经网络在水轮发电机轴承故障诊断中的应用[J].电网与清洁能源,2013(4): 62-66. ZHANG Fengli,CHEN Wenxian,JIA Haiying. Application of support vector machine and BP neural network in fault diagnosis of turbine bearing[J]. Power System and Clean Energy,2013(4): 62-66(in Chinese).
[20]王小根,龙海侠,孙俊.基于高斯扰动的量子粒子群优化算法[J].计算机应用研究,2010,27(6):2093-2096. WANG Xiaogen,LONG Haixia,SUN Jun. Quantumbehaved particle swarm optimization basedon Gaussian disturbance[J]. Application Research of Computers,2010,27(6):2093-2096(in Chinese).
[21]陈道君,龚庆武,金朝意,等.基于自适应扰动量子粒子群算法参数优化的支持向量回归机短期风电功率预测[J].电网技术,2013,37(4): 974-980. CHEN Daojun,GONG Qingwu,JIN Zhaoyi,et al. Shortterm wind power prediction based on support vector regression machine optimized by adaptive disturbance quantum -behaved particle swarm optimization[J]. Power System Technology,2013,37(4): 974-980(in Chinese). [22]习伟,李鹏,郭晓斌,等.多维时间序列关联分析方法在电力设备故障预测中的应用[J].电网与清洁能源,2014(12): 60-65.
XI Wei,LI Peng,GUO Xiaobin,et al. Application of correlation analysis method based on multi-dimensional time series in prediction of equipment faulture[J]. Power System and Clean Energy,2014(12): 60-65(in Chinese).
[23]潘迪夫,刘辉,李燕飞.风电场风速短期多步预测改进算法[J].中国电机工程学报,2008,28(26): 87-91. PAN Difu,LIU Hui,LI Yanfei. Optimization algorithm of short-term multi-step wind speed forecast[J]. Proceedings of the CSEE,2008,28(26): 87-91(in Chinese).
[24]连文莉,黄成辰,吕昌霖.采用时间序列预测风电场出力[J].电网与清洁能源,2011,27(12): 112-117. LIAN Wenli,HUANG Chengchen,LÜ Changlin. Wind farm output prediction based on time series[J]. Power System and Clean Energy,2011,27(12): 112-117(in Chinese).
邓旭阳(1983—),男,高工,从事电力系统继电保护管理相关工作;
林燕贞(1991—),女,硕士研究生,研究方向为电力系统继电保护风险评估;
陈志光(1965—),男,高工,从事电力系统继电保护管理相关工作;
龚庆武(1967—),男,教授,博士生导师,研究方向为电力系统运行与控制、优化调度等。
(编辑冯露)
Failure Rate Prediction Model of Relay Protection Equipment Based on Optimized LS-SVR
DENG Xuyang1,CHEN Zhiguang1,LIN Yanzhen2,GONG Qingwu2
(1. Power Dispatch Control Center of Guangdong Electric Power Co.,Ltd.,Guangzhou 510600,Guangdong,China;2. School of Electrical Engineering,Wuhan University,Wuhan 430072,Hubei,China)
ABSTRACT:The interconnected operation of the power system puts forward even higher requirements for the relay protection equipment and the safe and stable operation of the relay protection equipment is closely related to the failure rate. In order to solve the problem that the standard particle swarm optimization(SPSO)is trapped in local optimum,the Gauss perturbation operation is added and GDSPSO is put forward. And in the optimization process,the defect of the traditional learning factor which is the fixed value is changed,and the expression of the learning factor is introduced,the algorithm search capabilities are changed. The learning parameters of least square support vector machine(LS-SVR)are optimized,and the prediction model is established and the error analysis is done. Finally,the same model and the same operating environment of 24 relay protection equipment are taken as an example,the GDSPSO is compared with other three algorithms,the comparison result shows that the algorithm proposed in this paper is fast and with good stability,and the computation time is short. And results and the forecast precision of the forecasting model based on the learning parameters obtained by GDSPSO optimization are good and high.
KEY WORDS:relay protection equipment;failure rate prediction;LS-SVR;SPSO;GDSPSO;learning factor
作者简介:
收稿日期:2015-08-23。
基金项目:国家科技支撑计划课题资助(2013BAA02B01)。
文章编号:1674- 3814(2016)03- 0025- 09
中图分类号:TM774
文献标志码:A

