一种基于自由振荡主频实现故障测距的方法

苏凤，王选诚，董云云，孙玉梅，高翔，杨海利

（1.烟台南山学院工学院，山东烟台　265713；2.山东烟台南山集团东海热电有限公司，山东烟台　265713）



一种基于自由振荡主频实现故障测距的方法

苏凤1，王选诚1，董云云1，孙玉梅1，高翔1，杨海利2

（1.烟台南山学院工学院，山东烟台265713；2.山东烟台南山集团东海热电有限公司，山东烟台265713）

摘要：准确测量出故障点的位置是系统保护能正确操作的前提，但对于经过过渡电阻接地的故障，依靠传统的方法很难准确测出故障距离。而且在超/特高压输电线路中，由于分布电容不能忽略，这增加了故障测距的难度。分析了过渡电阻对距离保护的影响，进而提出了一种利用分布电容引起的自由振荡主频频率的大小实现故障测距的方法。通过PSCAD/ EMTDC仿真结果验证了新方法的有效性。

关键词：过渡电阻；分布电容；自由振荡频率；T型等效；故障距离

Project Supported by the Fundamental Research funds for the Central Universities（2015XS16）.

距离保护一直是我国线路保护中的经典保护之一，它能够快速切除线路中任意内部故障，并且对金属性接地故障能起到天然的测距作用。但在现实故障中，金属性接地故障所占比例较低[1-2]，一般都是通过一定的过渡电阻形成接地故障，这就对故障测距提出了新的要求[3]。

高/超压线路中分布电容较大，而分布电容容易引起非工频暂态分量[4-6]，这对我国经典的基于工频分量的继电保护是巨大的挑战。但正因为分布电容的存在，一些基于暂态量的保护方法得到了很快的发展，如行波保护、边界保护等[7-9]。而本文关注的是由于分布电容引起的暂态高频分量在频域上的特征，进而提出利用自由振荡主频进行故障测距的方法。

笔者首先在频域上分析了自有振荡频率产生的机理，然后讨论了自由振荡频率的影响因素，发现自由振荡频率的大小与故障点发生的距离成反比，因此可以利用两者的反比关系准确求出故障距离。最后基于PSACD/EMTDC仿真验证了方法的正确性。

1　过渡电阻对距离保护的影响

图1为线路经过渡电阻接地故障时电路示意图。图1中Rg为过渡电阻；Im，In分别为流过线路两侧的电流；IK为流过短路点的电流，短路点用K表示，Z1m为保护安装处到短路点处的短路阻抗。

以M侧为例进行分析过渡电阻对距离保护的影响。由电路原理可得出M侧测量阻抗表达式为

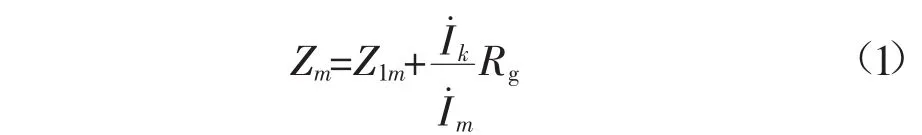
Rg对测量阻抗的影响取决于双侧电源提供的短路电流之间的夹角的性质：若滞后于，则具有负的阻抗角，即表现为容性的阻抗，即过渡电阻的存在可能使总的测量阻抗变小；反之，具有感性的阻抗，它的存在可能使测量阻抗变大。所以测量阻抗会因为过渡电阻的存在使Zm不能正确反映短路阻抗Z1m的大小，进而影响到故障测距的准确性。因此研究在经过过渡电阻故障条件下进行准确的故障测距方法具有十分重要的意义。

图1　线路经过过渡电阻接地网络图Fig. 1 The network of line through transition resistance

2　自由振荡主频频率的研究

如图2所示，双端系统在F点发生三相短路故障，短路点距M侧的距离为d。利用一个T型网络等值输电线路，在频域中，系统M侧故障附加网络示意图如图3所示。

图2　短路故障示意图Fig. 2 The short fault diagram

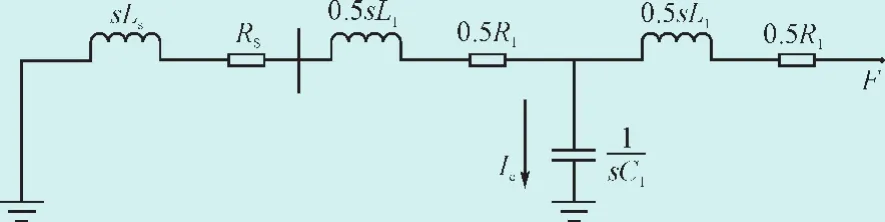
图3　用T型网络等效电路图Fig. 3 The T network equivalent circuit

图3中，F为故障点，ZS=RS+sLs是电源阻抗，R1，L1，C1分别表示输电线路的电阻、电感和电容。由于全系统阻抗角几乎相等[8]，因此可以假设ZS与Z1的阻抗角相等，不妨表示为Ls=mL1，RS=mR1，其中m=

由图3可以列写出电容电流的特征方程为

式中：

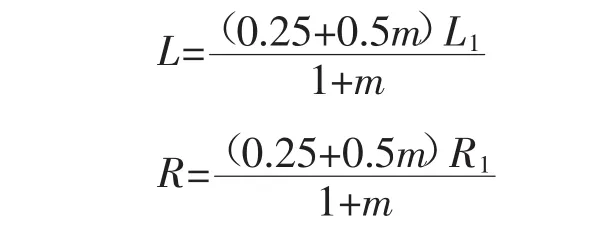
式（2）解的特征根为

式中，s1对应的是衰减时间常数的倒数；s2，3为一复数，其实部对应自由振荡主频的衰减时间常数的倒数，虚部对应着自由振荡主频的角频率w1，所以自由振荡主频频率f可表示为

由于在超/特高压线路中电阻分量相对电抗分量较小，可以忽略不计，因此式（3）可以进一步简化为

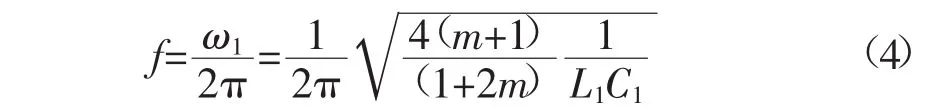
考虑到L1=l1d，C1=c1d，式（4）可以进一步化简为

式中：l1，c1分别为单位长度的输电线路的电感和电容。

通过式（5）可以看到自由振荡主频频率的大小与短路点距保护安装处的距离d成反比，因此只要知道发生短路时自由振荡主频频率的大小，便可以准确求出故障距离。两者的关系如图4所示。需要指出的是式（5）中m线路的基本参数可以作为已知数值输入到保护装置中。

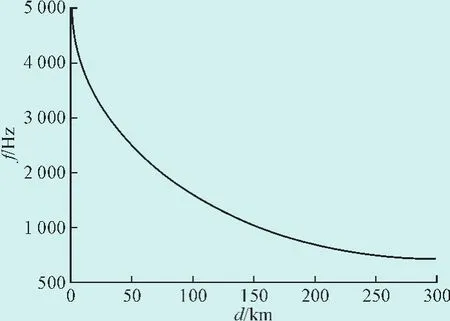
图4　自由振荡频率随距离变化的曲线Fig. 4 The curve of the free oscillation frequency with fault distance changes

3　仿真验证

3.1过渡电阻对自由振荡主频的影响

基于PSCAD/EMTDC仿真软件搭建了图5所示的仿真模型，MN线路长度为400km，线路正序参数为L11= 0.892 mH/km，R11=0.013 33 Ω/km，C11=13.2 nF/km，R11=0.321 64 Ω/km。负序参数为L0=2.063 mH/km，C0=9.55 nF/km。系统S1正负序参数为Zs1=（2.33+j49）Ω，Zs10=（3.00+j18.4）Ω，E˙S1=1.106 2∠0°。系统S2正负序参数为Zs2=2.70+j56.732 Ω，Zs20=（2.53+j14.98）Ω，E˙S2=1.106 9∠-44°。设置F1～F33处故障点，距M母线距离分别为100 km，200 km，350 km。故障时间为0.5 s，采样频率为100 kHz。

图5　PSACD/EMTDC仿真模型Fig. 5 The simulation model based on PSCAD/EMTDC

图6的仿真图形表示线路经过不同的过渡电阻接地时，自由振荡主频的变化情况。

表1列出了在不同过渡电阻发生故障时计算得到的自由振荡主频频率的数值。通过表1可以看出，自由振荡主频的频率大小受过渡电阻的影响很小（除非过渡电阻非常大[3]，但出现如此大的过渡电阻在现实工况中很少出现）。通过图6（a）—图6（d）对比可以看出，过渡电阻的大小只是影响了自由振荡主频的幅值，而对频率的大小几乎没有影响。因此基于自由振荡主频频率实现故障测距从原理上是可行的。

表1　表示不同过渡电阻下的自由振荡主频Tab. 1 The main free oscillation frequency on the different resistances

3.2利用自由振荡主频实现测距仿真

当故障发生在距离母线M 350 km时保护1处得到的电流波形如图7（a）所示。由图可以看出，故障后的波形中存在很多毛刺，由此可知故障后的波形中除了基波分量外，还含有大量的自由振荡频率分量，自由振荡频率谱如图7（b）所示。

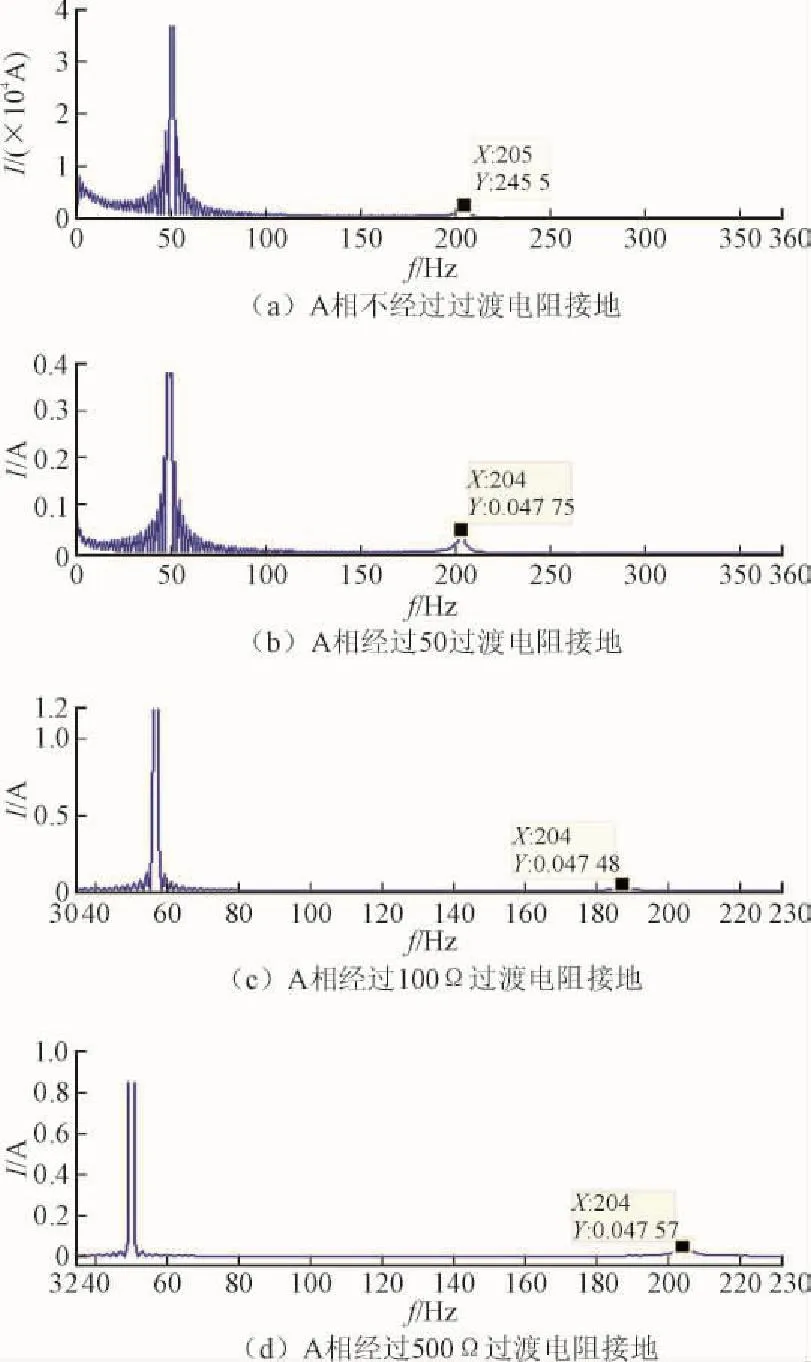
图6　不同过渡电阻下自由振荡主频频率关系示意图Fig. 6 The relationship between the fault resistance and the main free oscillation frequency

图7　短路测量电流及其频谱Fig. 7 Measuring current and its spectra in short circuit

表2列出了在F1～F33点发生故障时计算得到的短路距离与实际短路距离的对比结果。通过表2可以看出计算结果与实际值相差不大。但当故障点离着保护安装处越远时，计算误差随着增大，这是由于自由振荡主频的推导是根据1个T型网络推导出来的，而当线路较长时，1个T型网络的准确度显然是无法达到精度要求的，如果多个T型网络进行等效的话，效果会变好。但当距离很短时，发现误差还是很小的，满足工程需要。

表2　计算值与实际值的比较Tab. 2 Comparison between the calculated and actual values

4　结语

参考文献

[1]徐振宇.现代距离保护技术的最新发展[J].电力设备，2008，9（12）: 35-39. XU Zhenyu. The development for modern distance protection[J]. Electric Equipment，2008，9（12）: 35-39（in Chinese）.

[2]何引生，胡玉生，商立群.基于故障相电压功率谱的超高压串补输电线路故障识别[J].电网与清洁能源，2014，30（8）: 48-52. HE Yinsheng，HU Yusheng，SHANG Liqun. Fault recognition for EHV transmission line with series capacitors based on power spectrum of fault phase voltage[J]. Power SystemandCleanEnergy，2014，30（8）: 48-52（in Chinese）.

[3]王兴国，黄少锋.过渡电阻对故障暂态份量的影响分析[J].电力系统保护与控制，2010，38（2）: 18-21. WANG Xingguo，HUANG Shaofeng. Impact of fault resistance for fault transient component[J]. Power System Protection and Control，2010，38（2）: 18-21（in Chinese）.

[4] YANG Q S，MORRISON I F. Micro-based algorithm for high-resistance earth-fault distance a protection[J]. Generation，Transmission and Distribution，IEEE Proceedings C，1983，130（6）: 306-310.

[5] YE P，LI K K. A novel algorithm for high-resistance earth-fault distance protection[C]// Transmission and Distribution Conference，1996，Los ANGELES，CA，1996: 475-480.

[6] FUNK A T. Impedance estimation including ground fault resistance error correction for distance protection[J]. International Journal of Electrical Power and Energy System，2000，22（1）: 59-66.

[7] YANG Changhong. Research on the ability of ultra-high voltage transmission line distance protection standing fault resistance influence[J]. Journal of Electric Power Science and Technology，2007，22（3）: 27-31.

[8]黄少锋，赵月，申洪明.一种高压输电线路故障暂态量自由振荡主频率的估算方法[J].电网技术，2012，36 （9）: 187-192 HUANG Shaofeng，ZHAO Yue，SHEN Hongming. A method to estimate main frequency of free oscillation in fault transient component of UHV transmission line[J]. Power System Technology，2012，36（9）: 187-192（in Chinese）.

[9]熊浩，蔡勇军，周平，等.串联补偿装置对500 kV万龙线路影响分析[J].电力电容器与无功补偿，2008，29（5）: 6-8，28. XIONG Hao，CAI Yongjun，ZHOU Ping，et al. Analysis of the influnence of series compensator on 500 kV Wanglong lines[J]. Power Capacitor & Reactive Power Compensation，2008，29（5）: 6-8，28（in Chinese）.

苏凤（1981—），女，硕士，讲师，主要研究方向为传感器与电路设计、电气与自动控制；

王选诚（1963—），男，学士，高工，主要研究方向为电气传动、电力电子与自动控制；

董云云（1981—），女，硕士，讲师，主要研究方向为测控与过程建模；

孙玉梅（1976—），女，硕士，高工，主要研究方向为嵌入式系统设计；

高翔（1967—），男，博士，副教授，主要研究方向为控制系统故障诊断，多元统计过程建模和监控，数据挖掘；

杨海利（1981—），女，学士，工程师，主要研究方向为电网监测与控制。

（编辑冯露）

新的故障测距方法是基于分布电容引起的自由振荡主频频率而实现精确测距的，因此新的方法不受分布电容的影响；同时过渡电阻的存在只会影响到自由振荡主频的幅值，但对自由振荡主频频率影响不大。考虑到工程中不需要精确计算短路距离，只需要知道一定的故障范围即可，因此该方法具有很大的工程应用价值。

A Method to Measure the Fault Distance Based on the Main Free Oscillation Frequency

SU Feng1，WANG Xuancheng1，DONG Yunyun1，SUN Yumei1，GAO Xiang1，YANG Haili2
（1. Technology Institute，Yantai Nanshan University，Yantai 265713，Shandong，China；2. Yantai Nanshan Group East China Sea Thermal Power Co.，Ltd.，Yantai 265713，Shandong，China）

ABSTRACT：Accurately measuring the fault point is the foundation for the correct operation of the relay protection. However，it is very difficult to measure the fault location accurately when the fault is through the transition resistance in the conventional method. In addition，the distributed capacitance in the high -voltage transmission lines makes the measurement method more complicated. This paper first analyzes the impact of the transition resistance on the distance protection and then proposes a method based on the frequency of free oscillations to measure the fault position. At last the simulation results prove the method to be reasonable.

KEY WORDS：transition resistance；distributed capacitance；free oscillation frequency；T equivalent；fault distance

作者简介：

收稿日期：2015-09-02。

基金项目：中央高校基本科研业务专项基金资助（2015XS16）。

文章编号：1674- 3814（2016）03- 0068- 04

中图分类号：TM744

文献标志码：A