基于Kernel K-means的负荷曲线聚类

赵文清，龚亚强

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引言

电力负荷曲线聚类是配用电大数据挖掘的基础［1］。负荷曲线聚类一直是电力负荷预测、分时电价、错峰管理、系统规划的基础，通过负荷分类和负荷特性分析，对于掌握电力负荷的变化规律和发展趋势具有重大意义。高效的负荷聚类方法能为电力规划、错峰管理等提供可靠的依据和准确的指导［2］。因此，研究准确的负荷曲线聚类具有重要意义。

电力负荷曲线的聚类分析，实际上就是衡量不同负荷曲线的相似性，以及把负荷曲线分类到不同的簇中。这就需要根据负荷特性进行准确、科学分类，以确保在同一类中的负荷曲线具有相同或相似的负荷特性，进而合理地确定典型负荷曲线的归类。在良好分类的基础上，可以进一步提高负荷预测精度、降低负荷管理的难度。聚类的结果要满足类内具有较高的紧密性，类间具有较高的分离性，体现出不同类型用户之间的负荷特性差异［3］。

目前的电力负荷曲线聚类的方法很多，比较流行的有 K-means 聚类［4］、小波分析［5］、模糊 C 均值聚类算法（FCM）［6］、集成聚类算法［1］、自组织特征映射神经网络（SOM）［7］、极端学习机（ELM）［8］、云模型［9］等，同时还有一些在这些算法的基础上进行改进的算法。

由于智能电网技术的快速发展，各种先进的检测装置和计量设备在配电网中取得了广泛的应用。对负荷的检测的时间越来越短，导致负荷数据的维数大幅提高，加大了负荷曲线聚类的难度。为了解决该问题，本文采用核方法将数据映射到高维空间中，加大数据的可分性，从而提高负荷曲线聚类的效果。

1 Kernel K-means

1.1 核函数

核方法是将数据映射到高维空间中，从而使数据可分性在高维空间中增大，聚类的效果相应地得到提升［10］。核方法对映射到高维空间的维度并没有太多的限制，高维空间甚至可以是无限维的。

核函数为核方法提供了一种映射的方式。核函数通过点积的方式将数据在高维空间中的关系表示出来，降低了在高维空间中讨论数据映射的难度。下面将描述核函数是如何表示数据在高维空间的关系。

假设给定一组样本数据 x1、x2、…、xn，xiϵRD，即每个样本数据为D维向量，映射方程φ（x）将xi从空间RD映射到新空间Q，则核函数在新空间Q定义的点积为：

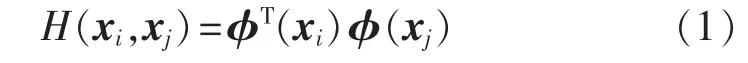
其中，无需知道变换函数φ（x）的形式和参数，映射实际上是通过核函数H（xi，xj）完成的，即只需要给定核函数的形式就能完成数据从低维空间到高维空间的映射。常用的核函数有：多项式核函数H（xi，xj）=（xi·xj+1）d、高斯核函数H（xi，xj）=exp（-r‖xi-xj‖2）、感知器核函数H（xi，xj）=tanh［a（xi·xj）+d］。

通过上述方式，核函数可以轻易地将低维空间与高维空间联系起来。核函数方法可以和不同的算法相结合，形成多种不同的基于核函数技术的方法，而且这两部分的设计可以单独进行，并可以为不同的应用选择不同的核函数和算法。如SVM（Support Vector Machine）、Kernel K-means算法、核主成分分析 KPCA（Kernel Principal Component Analysis）等都是核函数与不同算法的结合。

1.2 算法描述

负荷曲线聚类的经典聚类分析方法有基于层次、基于划分、基于密度、基于模型等聚类算法，经典聚类算法各有优缺点［1］，本文为了进一步提高聚类划分的效果，采用Kernel K-means算法对负荷数据进行研究。

Kernel K-means算法是K-means算法的推广，也可以看作是它的一般形式。在K-means算法中，点与点之间的相似性是用距离来衡量的，但在Kernel K-means算法中，用核函数代替距离的作用衡量相似性。这样就相当于将数据的整个距离结构改变，同时也可以看作是将数据映射到一个新的空间。Kernel K-means算法描述如下。

设 A=｛x1，x2，…，xn｝为 n 个样本的数据集，划分A 为 K 类，Ck（k=1，2，…，K）代表一个聚类，δ（xi，Ck）表示指示函数，对应各个样本的所属类别k。φ（xi）表示 xi（i=1，2，…，n）从空间 RD到新空间 Q 的变换，在核空间Q中，聚类Ck对应的类中心为mk，公式如下：

其中，表示聚类Ck中的样本个数。

空间RD中任意2点间的距离通过核函数表示为内积的公式如下：

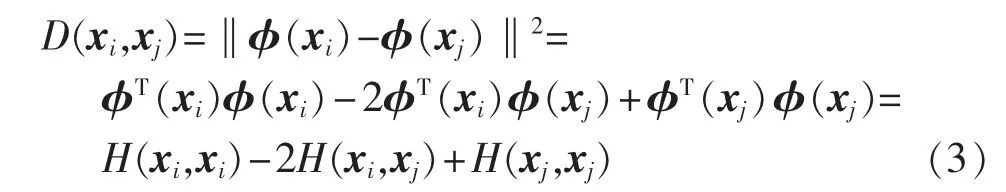
其中，选取高斯核作为核函数 H（xi，xj）。

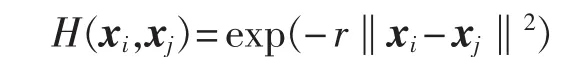
同理，类中每点xi到类中心mk的距离在新空间可表示为 D（xi，mk）=‖φ（xi）-mk‖2。

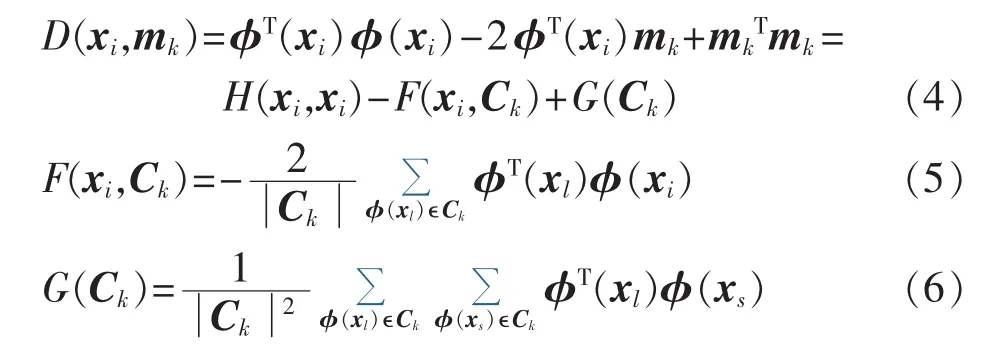
1.3 算法流程

Kernel K-means描述如下：

a.随机初始化分类向量 δ（xi，Ck），构造初始聚类 C1、C2、…、CK；

b.计算；

c.计算 F（xi，Ck），将 xi分配到最近的聚类中；

d.重复步骤 b、c，直到 δ（xi，Ck）不再变化。

2 算法优化

2.1 核主成分分析

主成分分析PCA（Principal Component Analysis）是一种确定一个坐标系统的直交变换。在这个新的坐标系统下，变换数据点的方差沿新的坐标轴可以得到最大化。这些坐标轴经常被称为是主成分。PCA运算是一个利用了数据集的统计性质的特征空间变换。这种变换在无损或很少损失数据集的信息的情况下降低了数据集的维数［12］。

KPCA是线性PCA的非线性扩展算法，它采用非线性的方法抽取主成分，即KPCA是在通过映射函数把原始向量映射到高维空间F，在F上进行PCA［12］。 文献［13］提出一种大规模数据集求解核主成分的计算方法，该方法首先利用Gram矩阵构造一个Gram-power矩阵，然后将Gram矩阵的每一列作为每一步迭代算法的输入样本［13］。利用该方法可以有效解决传统方法在大规模数据集下无法使用的问题。

KPCA与PCA具有本质上的区别：PCA基于指标，而KPCA是基于样本的。KPCA不仅适合解决非线性特征提取问题，而且它还能比PCA提供更多的特征数目和更多的特征质量。因为KPCA可提供的特征数目与输入样本的数目是相等的，而PCA的特征数目仅为输入样本的维数。KPCA的优势是可以最大限度地抽取指标的信息，但是KPCA抽取指标的实际意义不是很明确［12］。

2.2 核矩阵的削减

从Kernel K-means算法中可以得出，比较样本与类中心距离大小需要计算2个样本的内积。本文中将数据集中任意2个样本间的内积计算出来，组成核矩阵［12］。核矩阵H为n×n阶矩阵，其中：

N条负荷曲线构成数据集合。其中，每条负荷曲线都是由 D 维的向量组成。如果要构造这样一个核矩阵，矩阵的储存空间将为 O（N2）。 当 N 较大时，矩阵计算量将会很大［11］。文献［14-16］为了提高计算的效率，分别提出不同的解决策略。本文按照保留核矩阵中值较大的项、去除核矩阵中较小值的原则，再依据给定规则将核矩阵的某些项归零［11］。这样，可以减少计算时间，提高运算效率。这种对核矩阵削减的算法描述如下。

a.将核矩阵H各行按升序进行排列，每行得到一个排序向量 ri：rij（i=1，2，…，n；j=1，2，…，n）。

b.计算rij的一阶导数，公式如下：

c.以降序方式排列 r′ij（j=1，2，…，n）。 若为排序的前10%，则令vij=1；否则，vij=0。10%为所给定的阈值。 得到的二值化向量 vi，vi=［vi1，vi2，…，vin］T。

e.根据v*计算得分向量s，公式如下：

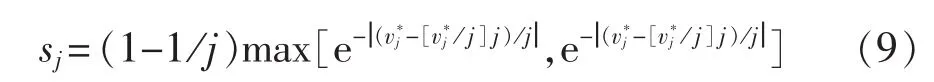
f.取 s中最大值所属聚类 j，即，定义：对任一数据样本ai，其二值向量为 vi，如果viw=1，则ai属于基数为w的聚类；否则不属于聚类w。任一数据样本ai，若使聚类基数w值有所增加，必然属于聚类w。

g.令 v*=v*-vi，若 v*≠0，进行下一次迭代，重复步骤 d、e；若 v*=0，进入下一行，重复步骤 b—g。

h.假设ai所属的聚类基数为wi，在第i行中，保留［H］ij值中较大的前wi项，其余所有项全部设置为0。削减后的核矩阵记为H*，其中的非0项个数记为nz。

3 实验分析

3.1 聚类评估指标的选取

聚类分析是按照样本的特征将其分类到不同的类的过程，使同一类的个体具有尽可能高的相似性，而类别间则具有尽可能高的互异性。由于聚类分析是在没有先验信息指导下的无监督学习过程，因此评价聚类的效果在聚类分析中至关重要。

本文采用Davies-Bouldin指标评价聚类质量并确定最佳聚类数，其计算公式如下：

其中，Ri用来衡量第i类与第j类的相似度。

其中，Si用来度量第i个类中数据点的分散程度，计算公式如式（12）所示。

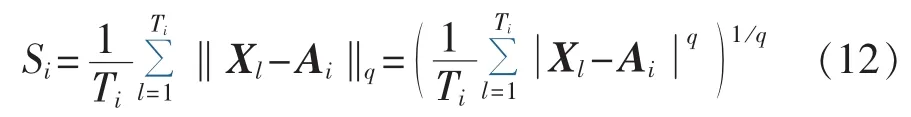
其中，Xl为第i类中第l个数据点；Ai为第i类的中心；Ti为第i类中数据点的个数；q取1时Si为各点到中心的距离的均值，q取2时Si为各点到中心的距离的标准差，它们都可以用来衡量类内分散程度。

其中，Mij为第i类中心与第j类中心的距离；adi为第i类的中心点Ai的第d个属性的值；p取1时表示1-范数，p取2时表示2-范数（表示2个类中心的欧氏距离）。

DBI是类内距离之和与类外距离的比值。类内对象距离越小，类间距离越大，DBI指标也越小，聚类效果越好。DBI也可以优化K值的选择，最小的DBI指标对应的K就是最佳聚类个数。

3.2 实验数据

实验数据［17］取自由美国能源部于2009年12月成立的 OpenEI（Open Energy Information）。 OpenEI是为政策制定者、研究人员、技术投资者、风险资本家及市场专业人士提供能源数据、信息等其他资源的网站。部分实验数据如表1所示。

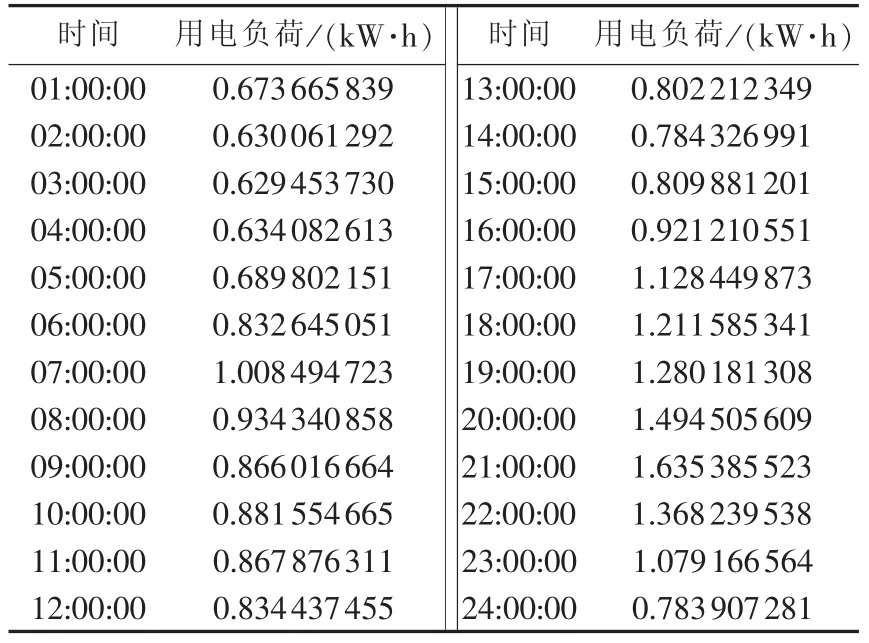
表1 24 h居民负荷数据Table1 Hourly data of residential load

3.3 结果分析

实验采用的机器配置为 Intel（R）Core（TM）i3-3110M 8-core CPU@2.40 GHz，4 GB RAM，MATLAB版本为MATLABR2014b。

首先考察KPCA对聚类效果的影响。当采用KPCA进行降维后，输出的维度对聚类效果有较大的影响，比如取输出维度为［1，30］时，聚类效果如图1所示。

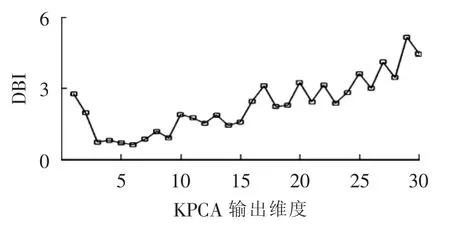
图1 输出维度对聚类效果的影响Fig.1 Effect of output dimension on clustering

由图1可知，输出维度的大小与聚类效果不是正比关系，当输出的维度太大或者太小，都不会得到最优聚类。当输出维度为6时，得到DBI的值最小，聚类的结果最为理想。因此核主成分分析取6作为输出维度。

实验再对聚类数与聚类效果进行分析，分别采用3种算法进行对比分析。第1种算法是传统的K-means；第2种算法是Kernel K-means，即采用了核方法的K-means；第3种算法KPCA-K-K-means首先使用KPCA进行降维处理，从而得到降维后的核矩阵，再削减核矩阵，最后使用K-means进行聚类。利用MATLAB对上述3种算法编程，考察不同聚类数对聚类效果的影响，K-means、Kernel K-means、KPCAK-K-means以聚类数作为输入，其中Kernel K-means与KPCA-K-K-means的核函数都选取高斯核函数，参数分别取r1=-0.1、r2=-1。聚类数与DBI对应关系如表2所示。

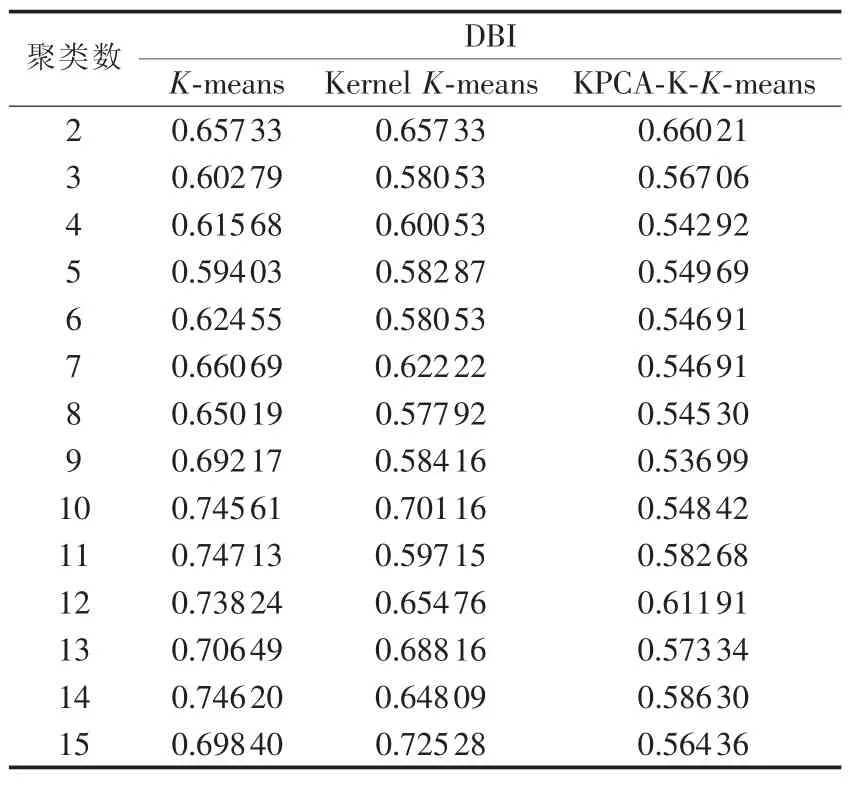
表2 聚类数与DBI的关系Table 2 Relationship between clustering number and DBI

由于3种算法的聚类效果都会受初始点的影响，因此对每个算法每一聚类数K，分别运行10次，取最小的DBI值作为该算法的性能表现。表2对应的曲线图如图2所示。

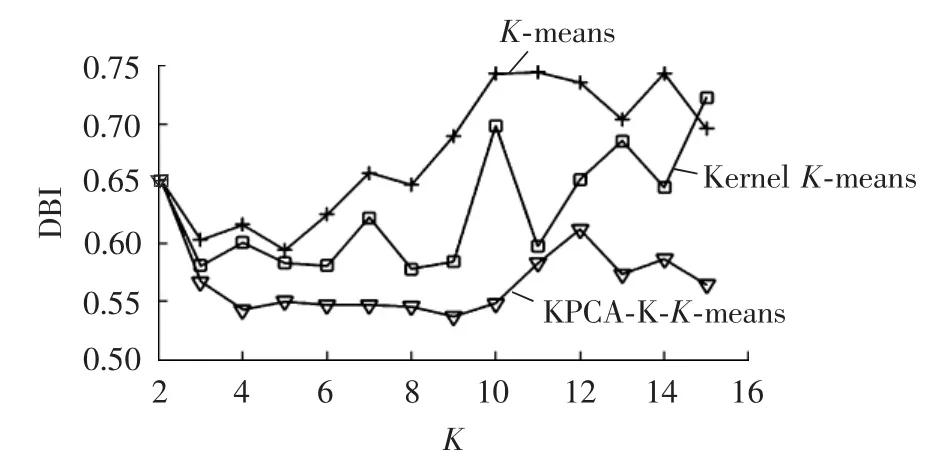
图2 聚类数与DBI的关系曲线Fig.2 Chart of relationship between clustering number and DBI

从图2可以看出，当聚类数取值相同时，各算法所得DBI值中，K-means算法最大，Kernel K-means次之，KPCA-K-K-means最小。在聚类数的取值不同时，KPCA-K-K-means取 得的 DBI值 比 K-means、Kernel K-means 2种算法得到的DBI值都要小，可以得出KPCA-K-K-means算法对负荷曲线的划分更加合理，可以提高聚类的准确度。从图中还可得出，当聚类数K=5时，曲线具有明显的拐点，由此可以确定最佳聚类数。

4 结论

本文针对负荷数据出现的新特点，提出使用KPCA方法对负荷数据进行降维，同时保持数据在高维空间中的映射，使数据具有较好的可分性，然后根据聚类算法Kernel K-means的原理，对负荷曲线进行划分。实验探究了不同聚类数与聚类效果的关系以及输出维数对聚类效果的影响，表明本文方法可以有效地提高负荷曲线聚类的准确性。但该方法聚类易受聚类数和初始分类影响，需要提前确定核函数参数，以及运行时间增大等问题并没有完全解决，这也是进一步的研究方向。

［1］张斌，庄池杰，胡军，等.结合降维技术的电力负荷曲线集成聚类算法［J］. 中国电机工程学报，2015，35（15）：3741-3749.ZHANG Bin，ZHUANG Chijie，HU Jun，et al.Dimensionality reduction technique combined with power load curve integrated clustering algorithm［J］.Proceedings of the CSEE，2015，35（15）：3741-3749.

［2］朱晓清.电力负荷的分类方法及其应用［D］.广州：华南理工大学，2012.ZHU Xiaoqing.Classification of power load and its application［D］.Guangzhou：South China University of Technology，2012.

［3］张忠华.电力系统负荷分类研究［D］.天津：天津大学，2007.ZHANG Zhonghua.Load classification of power system ［D］.Tianjin：Tianjin University，2007.

［4］白雪峰，蒋国栋.基于改进K-means聚类算法的负荷建模及应用［J］. 电力自动化设备，2010，30（7）：80-83.BAI Xuefeng，JIANG Guodong.Load modeling based on improved K-means clustering algorithm and its application［J］.Electric Power Automation Equipment，2010，30（7）：80-83.

［5］张平，潘学萍，薛文超.基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测［J］. 电力自动化设备，2012，32（11）：121-125，141.ZHANG Ping，PAN Xueping，XUE Wenchao.Short-term load forecasting based on wavelet decomposition，fuzzy gray correlation clustering and BP neural network［J］.Electric Power Automation Equipment，2012，32（11）：121-125，141.

［6］刘永光，孙超亮，牛贞贞，等.改进型模糊C均值聚类算法的电力负荷特性分类技术研究［J］. 电测与仪表，2014，51（18）：5-9.LIU Yongguang，SUN Chaoliang，NIU Zhenzhen，et al.Research on the improved fuzzy C-means clustering algorithm based power load characteristic classification technology［J］.Electrical Measurement&Instrumentation，2014，51（18）：5-9.

［7］李智勇，吴晶莹，吴为麟，等.基于自组织映射神经网络的电力用户负荷曲线聚类［J］. 电力系统自动化，2008，32（15）：66-70，78.LI Zhiyong，WU Jingying，WU Weilin，et al.Power customers load profile clustering using the SOM neural network［J］.Automation of Electric Power Systems，2008，32（15）：66-70，78.

［8］张少敏，赵硕，王保义，等.基于云计算和量子粒子群算法的电力负荷曲线聚类算法研究［J］. 电力系统保护与控制，2014，42（21）：93-98.ZHANG Shaomin，ZHAO Shuo，WANG Baoyi，et al.Research of power load curve clustering algorithm based on cloud computing and quantum particle swarm optimization［J］.Power System Protection and Control，2014，42（21）：93-98.

［9］宋易阳，李存斌，祁之强.基于云模型和模糊聚类的电力负荷模式提取方法［J］. 电网技术，2014，38（12）：3378-3383.SONG Yiyang，LI Cunbin，QI Zhiqiang.Extraction of power load patterns based on cloud model and fuzzy clustering［J］.Power System Technology，2014，38（12）：3378-3383.

［10］TZORTZIS G F，LIKAS A C.The global Kernel K-means algorithm for cluster in feature space［J］.IEEE Transactions on Neural Networks，2009，20（7）：1181-1194.

［11］TSAPANOS N，TEFAS A，NIKOLAIDIS N，et al.A distributed framework for trimmed Kernel K-means clustering［J］.Pattern Recognition，2015，48（8）：2685-2698.

［12］史卫亚，郭跃飞，薛向阳.一种解决大规模数据集问题的核主成分分析算法［J］. 软件学报，2009，20（8）：2153-2159.SHI Weiya，GUO Yuefei，XUE Xiangyang.Efficient kernel principal component analysis algorithm for large-scale data set［J］.Journal of Software，2009，20（8）：2153-2159.

［13］胡中中.图像信息多层次融合技术的研究［D］.南昌：南昌大学，2012.HU Zhongzhong.The research of multi-level fusion technology about image information［D］.Nanchang：Nanchang University，2012.

［14］ZHANG R，RUDNICKY A I.A large scale clustering scheme for Kernel K-means［C］∥International Conference on Pattern Recognition.Quebec City，Canada：IEEE，2002：289-292.

［15］CHITTA R，JIN R，HAVENS T C，et al.Approximate Kernel K-means：solution to large scale kernel clustering［C］∥ACM SIGKDD International Conference on Knowledge Discovery and Date Mining.San Diego，California，USA：［s.n.］，2011：895-903.

［16］SARMA T H，VISWANATH P，REDDY B E.A fast approximate Kernel K-means clustering method for large data sets［C］∥Recent Advances in Intelligent Computational Systems（RAICS）.Trivandrum，India：IEEE，2011：545-550.

［17］ERIC W.Commercial and residential hourly load profiles for all TMY3 locations in the United States［EB／OL］. （2013-07-02） ［2016-04-25］.http： ∥en.openei.org／datasets／dataset／commercialand-residential-hourly-load-profiles-for-all-tmy3-locations-in-theunited-states.