基于动态修正技术的电力变压器可靠性评估模型研究
郭晓斌 ,程乐峰 ,王国平 ,许爱东 ,简淦杨 ,余 涛,魏文潇
(1.南方电网科学研究院,广东 广州 510080;2.华南理工大学 电力学院,广东 广州 510640)
0 引言
大型油浸式电力变压器作为电力系统的枢纽设备,其运行可靠性直接关系到电力系统的安全和稳定。因此,准确评估其可靠性水平是电网安全稳定运行的重要保证。在状态评估和维修方面,文献[1]提出基于云理论和前景理论的变压器状态维修策略综合评价模型,文献[2]提出基于合作博弈和云模型的变压器状态评估方法;在变压器可靠性分析方面,研究尚处于起步阶段,方法单一,理论发展不完善,其中,文献[3-4]通过故障树分析法对电力变压器可靠性进行了分析,文献[5]基于马尔可夫过程,建立了综合的变压器可靠性评估模型。这些研究方法大多基于统计规律,缺乏对变压器的个体差异性的考虑。变压器是由多个系统构成的复杂集合体,绕组油纸绝缘系统作为变压器最核心的部分,决定了变压器的寿命,其可靠性水平直接关系着变压器能否正常运行,准确评估其可靠性水平,对于防止绝缘故障过早发生具有重要意义[6]。目前,变压器油纸绝缘的相关研究主要集中在老化特征参量时效老化规律方面,对其可靠性评估方法的研究比较少,文献[7]在对相关特征参量进行深入分析的基础上,选取聚合度、糠醛体积分数等作为反映变压器油纸绝缘可靠性的特征参量,建立了混合威布尔(Weibull)模型,但是模型本身停留在实验室层面,考虑到现阶段供电企业不具备测试聚合度的条件,且很少对糠醛含量进行测试,特征参量获取比较困难。此外预防性试验规程规定糠醛的测试周期为6 a,期间变压器滤油、检修等操作对糠醛含量影响很大,影响了模型的准确性,这造成了模型推广的难度。相对而言,溶解气体分析DGA(Dissolved Gas Analysis)蕴含数据量大且数据容易获得,是研究变压器内部特性的首推特征量,DGA数据既可以离线获取也可以通过在线监测的手段获取,具有独特的优势。文献[8]针对油纸绝缘系统建立了热老化模型,但其输入维度单一,模型建立后不能根据变压器健康状态进行动态修正,模型尚未成熟。基于此,本文选取变压器油纸绝缘系统作为评估对象,取热点温度HST(Hot Spot Temperature)为核心点,结合Weibull分布和Arrhenius反应定律,建立了基于HST的变压器老化故障模型,并利用油中溶解气体分析数据,结合灰色理论对模型进行修正,确保评估值能反映变压器的实际可靠性水平。
1 基于HST的变压器老化故障模型
影响变压器油纸绝缘性能,造成绝缘老化的因素有多种,但变压器内部温度,特别是绕组HST对油纸绝缘系统的影响是最核心的[9]。鉴于目前变压器热点位置很难确定,且大部分已经服役的变压器并未预先安装温度传感器,后期植入传感器的实现难度较大[10-11],近年来,国际上推荐采用建立热模型对变压器热特性进行评估和研究。IEEE Std C57.91—2011和IEC Std 60076-7推荐了变压器绕组HST计算经验模型,前者对计算变压器顶层油温和绕组HST的经验公式进行了定义,即HST由环境温度、顶层油温或底层油温以及绕组热点对油温的温度梯度计算得到;后者假设绕组温升分布曲线(本文中为直线)与油温温升分布曲线为2条平行直线,即二者斜率相等,如图1所示。本文采用 IEEE规程[9]所给的HST计算方法计算绕组HST。

图1 油浸式变压器内部温度特性曲线Fig.1 Internal temperature characteristic curve of oil-immersed transformer
1.1 Weibull分布
Weibull分布是可靠性工程中非常重要的一种分布形式,其分布适应性非常好,可以模拟多种失效率变化形式。运用Weibull故障分布可以对递减和递增故障率进行建模,Weibull分布的故障率函数定义为:

其中,η 为尺度参数,η>0;β 为形状参数,β>0;t为时间,单位为a。η和β的值可通过最大似然估计法得到[7,12]。 根据形状参数 β 的不同,Weibull分布可简化为指数分布或瑞利分布,这使得其具有很强的兼容特性,通过参数的变化可以很好地表示不同分布特点的函数分布,因此该故障率表达式可以很好地对退化设备损耗时期的设备故障率进行描述。
1.2 计算绕组HST
变压器绝缘老化故障率与绕组HST存在非常紧密的联系,而HST主要取决于环境温度以及变压器所带的负荷,最热点常常位于电力变压器的高压绕组或低压绕组的顶部或中部。IEEE规程[9]推荐的HST计算流程如图2所示。

图2 绕组热点温度计算流程图Fig.2 Flowchart of winding HST calculation
图2中,K为变压器实际负荷与额定负荷的比值;R为额定负荷状态下的负荷损耗与空载损耗的比值;m和n为经验常数,其值与变压器的冷却方式有关;s为复频率;τω为在温度点位置的时间常数,单位为h;τTO为变压器油的时间常数,单位为 h;ΘA为瞬时环境温度,ΔΘTO,R为额定负荷下的顶层油温升,ΔΘH,R为额定负荷下HST相对于顶层油温的温升,ΔΘH、ΔΘTO和 ΔΘAe分别为绕组 HST相对于变压器顶部油温的增量、顶层油温相对于环境温度的温升及滞后的环境温度,单位都为℃。
根据图2得到绕组HST的计算式为:

1.3 变压器故障率λ计算
油浸式电力变压器绕组绝缘系统的老化过程是一个单向不可逆的过程,随着时间的推移,绝缘材料的机械性能、介电强度和电阻性能都会下降,如果变压器由于绝缘老化而失效,那么变压器的寿命也将终止。诺贝尔化学奖的获得者Arrhenius指出了绝缘材料在使用过程中,温度与绝缘材料化学反应速率的内在关系,并推导出著名的Arrhenius方程:

其中,L为绝缘材料的预期寿命;系数B、C与绝缘材料的种类、激活能量有关,可通过耐热试验测得;T为材料温度,即变压器持续运行时的绕组HST。
当Weibull分布应用于描述老化进程时,故障率由式(4)表示:
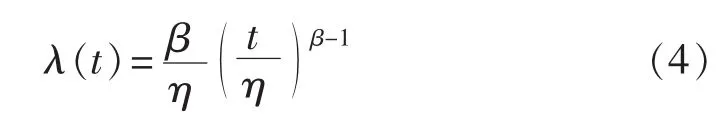
令η=L,则Arrhenius-Weibull模型的故障率函数为 λa(t|ΘH),将式(3)代入式(1),得到故障率函数如式(5)所示:

其中,参数β、B、C的求取通常采用最大似然估计法。本文充分参考国内外相关文献[13-19],采用了借助高斯分布来估计参数的新方法,具体包括2个步骤:首先,借助高斯分布中σ、μ的值对Weibull分布的参数η、β进行估算;然后,对于Arrhenius-Weibull模型,令β保持不变,用η的值来估算B和C的取值。
2 基于灰色理论的动态修正模型
在变压器正常老化条件下,上节建立的基础模型可以很好地反映油纸绝缘系统的故障率水平;但变压器投运之后,局部放电、高温过热等一些不可预知因素打破了正常老化的连续性,导致变压器绝缘恶化、故障率水平增高,基础模型的评估准确性大幅降低,此时就需要对模型进行修正,以保证曲线预测的准确性。
2.1 基于灰色理论的DGA修正模型
一般而言,变压器在正常工作状态下不产生特征气体,但是当变压器内部存在局部过热或电弧高温等故障时,会分解产生气体并不断溶解在变压器油中。气体的产生意味着变压器内部发生故障,内部故障缩短了变压器油纸绝缘系统的预期寿命,而变压器的预期寿命与HST满足指数关系[13]。因此,通过对变压器预期寿命的修正,可得到等效HST,进而实现将局部过热或电弧过热等故障对绝缘的影响用等效HST进行量化。
本文选取了 DGA 数据中的氢气(H2)、甲烷(CH4)、乙烷(C2H6)、乙烯(C2H4)、乙炔(C2H2)这 5 种气体作为电力变压器油纸绝缘状态的评估指标。这些气体与内部故障的对应关系如表1所示。使用灰色理论中的灰关联分析方法对数据进行处理,得到灰色靶心度Q(0.33≤Q≤1),评估对象的等级由靶心度决定,同时结合变压器的实际故障分布情况将变压器健康状态分为 5 个等级[20-22],分别为[0.9,1.0]、[0.6,0.9)、[0.5,0.6)、[0.4,0.5)和[0.33,0.4)。
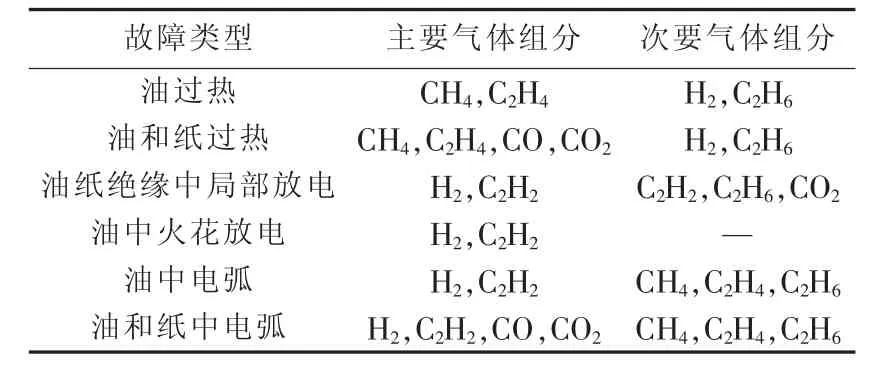
表1 不同故障类型产生的气体Table1 Gases generated by different fault types
变压器健康状态与变压器预期寿命存在着必然联系,即变压器运行状态良好,相应的变压器油纸绝缘系统的预期寿命就会延长;变压器健康状态恶劣,相应的变压器油纸绝缘系统劣化加快,预期寿命缩短。为了建立两者之间的对应关系,本文参考相对劣化度的模型架构[23-24],建立变压器预期寿命修正模型。
引入级差系数 αi(i=1,2,3,4)和 δi(i=1,2,3,4)来调整变压器油纸绝缘系统的故障程度与变压器预期寿命的对应关系,其中,αi用来调整靶心度与变压器预期寿命的比例关系;δi是考虑靶心度与变压器预期寿命可能不满足线性关系而引入的,δi值越大,对应的寿命缩短趋势越平缓,两者的值采用专家评测的方法确定,具体对应关系如下。
第1级别:靶心度范围为[0.9,1.0)。对应的变压器预期寿命修正系数为:

第2级别:靶心度范围为[0.6,0.9)。对应的变压器预期寿命修正系数为:
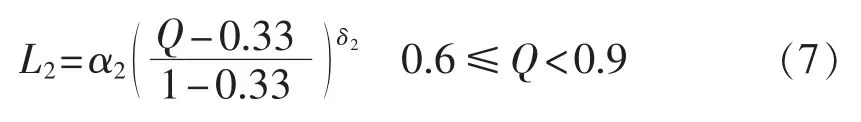
第3级别:靶心度范围为[0.5,0.6)。对应的变压器预期寿命修正系数为:

第4级别:靶心度范围为[0.4,0.5)。对应的变压器预期寿命修正系数为:
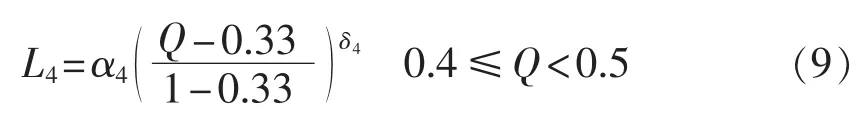
第 5级别:靶心度范围为[0.33,0.4)。 若能修好,根据变压器维修后的恢复情况,结合寿命损失恢复因子,再计算相应的故障率。
修正后的预期寿命Zeq:
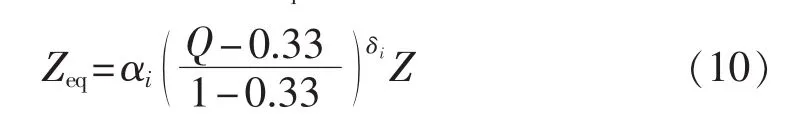
其中,Z为由基础模型求得的原始预期寿命。
则修正后的寿命损失量Z′:
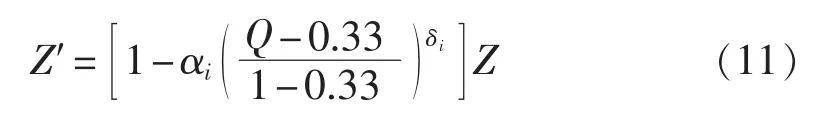
其中,αi、δi为经验值,需要根据实际变压器历史运行、检修数据进行确定。为了便于说明,本文假定变压器绕组绝缘系统的寿命损失量与变压器的状态量成严格正比例关系,取 αi= δi=1(i=1,2,3,4),则变压器各状态等级对应的寿命损失范围如表2所示。

表2 变压器绕组绝缘系统的状态等级与预期寿命的关系Table 2 Relation between status grade and expected life of transformer winding insulation system
可见,HST是基础评估模型和修正模型的连系纽带,灰色修正模型通过对变压器状态数据的处理,建立状态数据值和HST的对应关系,进而求得等效HST,实现了对基础模型的动态修正。
2.2 考虑检修后的模型修正方法
变压器在投运之后,根据变压器的运行情况会进行相应的检修(本文仅考虑变压器油纸绝缘系统的检修)。检修是变压器状态连续性的中断,经过检修后,变压器的预期寿命延长,对应的等效HST降低。结合役龄回退因子的概念[25-26],本文引入预期寿命损失恢复因子χ,变压器在经历大修或滤油等涉及绕组绝缘系统的维修后,预期寿命Z″可表示为:

其中,Z″为变压器新预期寿命;Z′为维修前一次修正后的预期寿命;Z′eq为维修前一次修正后的寿命损失量。由预期寿命和HST的对应关系,可得到该预期寿命下对应的等效HST,即Heq,从而实现对原始模型的修正。
修正后的故障率曲线是一条动态曲线,从几何意义来说,修正后的曲线由一条静态的指数曲线变成了一条动态阶梯状曲线。
3 实例分析
为验证本文所提的可靠性模型的有效性,以广东电网公司江门供电局某变电站110kV 2号主变压器为例进行计算分析,表3为变压器的设计参数。
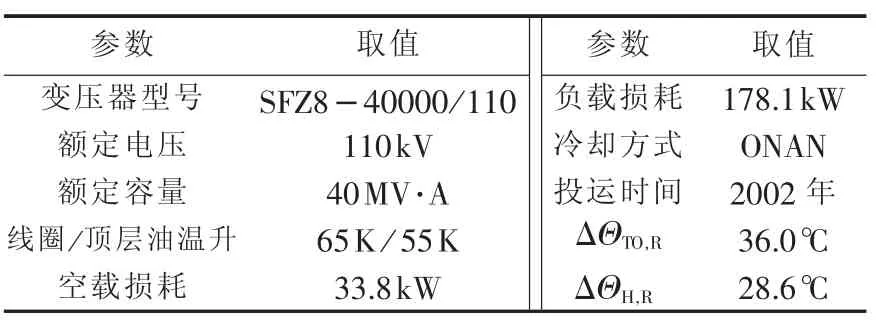
表3 待评估变压器的设计参数Table3 Design parameters oftransformer to be evaluated
表4为变压器可靠性评估模型的相应参数,其中χi为滤油时变压器的预期寿命损失恢复因子,χj为大修时变压器的预期寿命损失恢复因子,两者均为经验参数;τTO,R为额定负荷下变压器油的时间常数。
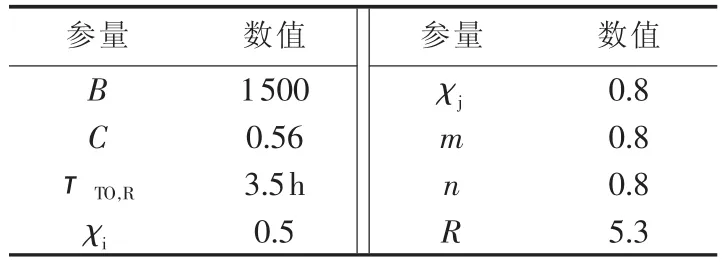
表4 相关系数取值表Table 4 Value of correlation coefficients
从江门气象局取得该地区历年的温度数据,统计区间为1957—2013年,其中,历年1月份平均气温如图3所示。

图3 江门市历年1月份平均气温变化曲线Fig.3 January average temperature curve of Jiangmen from 1957 to 2013
本文求取历年温度的平均值作为温度的基准值,即取57组温度数据的平均值,以月平均气温为基准,得到全年12个月的每月平均气温,其中1月份的平均气温为13.9℃,同理可求得其他月份的气温平均值,如表5所示。

表5 江门市月平均气温Table5 Monthly average temperatures of Jiangmen
为了更好地反映变压器所带负荷的大小,需要考虑以下两方面:
(1)短期内负荷是按日循环的,即日循环曲线;
(2)长期内变压器负荷是按年循环的,一年内随季节的不同,用电负荷会展现一定规律,为了全面把握负荷变动,同时考虑计算量和可行性。
基于上述2点,制定以下等效方案。
(1)取每月1日、11日、21日的负荷,全年取36d。
(2)以h为单位对负荷曲线进行量化。工程实践中,变压器负荷常用电流进行度量,本文延续这个做法,使用实际电流值与额定电流值的比值作为负荷率标幺值,选取2013年1月1日的HST计算方法进行说明,其变化率曲线如图4所示。
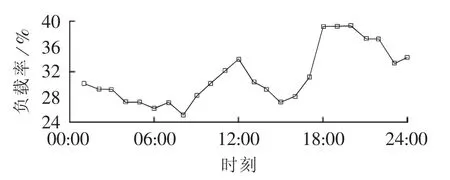
图4 主变负荷率曲线Fig.4 Load rate curve of main transformer
首先,求取变压器的HST,采用IEEE规程推荐的HST计算模型可以求得各个小时段的热点温升,如图5所示。
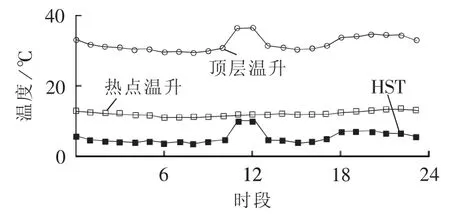
图5 温升曲线Fig.5 Temperature rise curve


文献[13]对154台电力变压器的寿命分布情况进行了统计分析,借助高斯分布确定了Arrhenius方程的经验值,借助MATLAB仿真得到HST与预期寿命对应曲线图,如图6所示。参照该对应关系,变压器在43.42℃的HST下预期寿命可达64.12a,将得到的温度与相应的参数代入故障率公式可得:
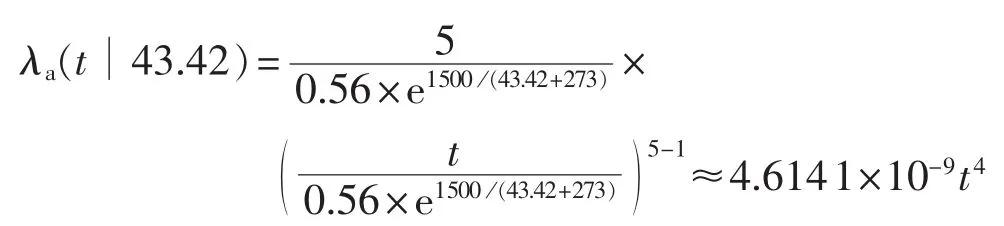
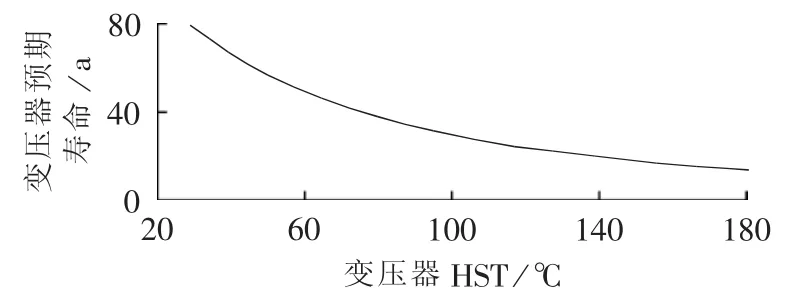
图6 变压器特征寿命与HST对应关系曲线Fig.6 Curve of expected life vs.HST of transformer
使用MATLAB对故障率公式进行仿真,可得变压器故障率随投运时间变化的关系曲线见图7。
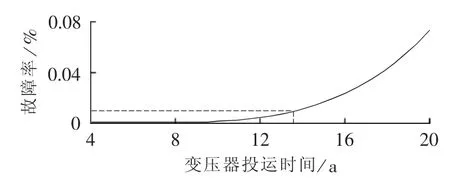
图7 变压器故障率曲线Fig.7 Failure rate curve of transformer
可见,投运12 a后,该变压器的故障率仅0.01%,是相当低的,这主要是由于变压器所带负荷控制在40%左右,变压器运行状态良好。但是变压器在实际过程中难免会出现短时过负荷、涌流等极端情况,同时,变压器在设计方面可能存在的缺陷也会对变压器的故障率产生比较大的影响。因此,必须结合变压器的实际情况对故障率曲线进行修正。由江门供电局检修所得到该变电站2号主变DGA测试数据值如表6所示。

利用HST与预期寿命对应关系图,可得到变压器的等效HST,Heq=48.53℃,得到变压器修正后的故障率曲线,如图8所示。

表6 2002到2014年DGA测试数据Table6 Data of DGA test from 2002 to 2014
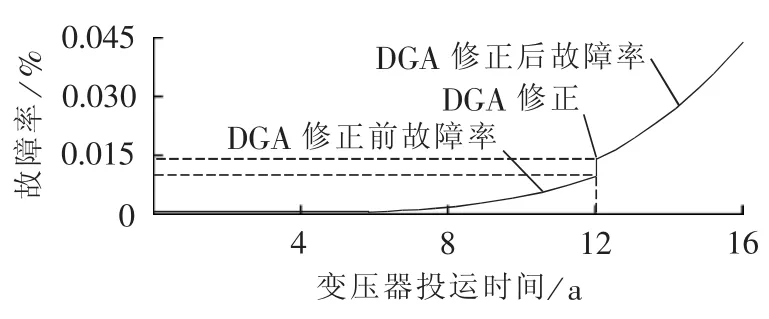
图8 DGA修正后的变压器故障率曲线图Fig.8 Failure rate curve of transformer after DGA correction
由于变压器DGA数据良好,所以修正后的故障率也只有0.014%。通过分析变压器各种预试数据并向运维人员核实,得到的情况为变压器运行状态良好,各项检测数据正常,从而验证了本文所提方法的正确性。
假设变压器从投运到现在已经有过1次检修,对应的DGA测试数据如表7所示。
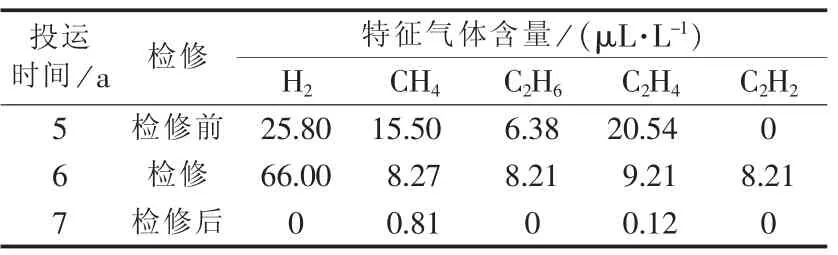
表7 变压器DGA数据参考值Table7 References of transformer DGA data
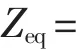
此时变压器的预期寿命降低至23.016 a,由HST和预期寿命对应曲线可得到变压器等效HST为130.66℃,故障率曲线如图9所示。
可见,如果不考虑检修的影响,运行到第6年故障率已经达到0.1%,内部绝缘情况已经开始劣化,故障率上升较快。
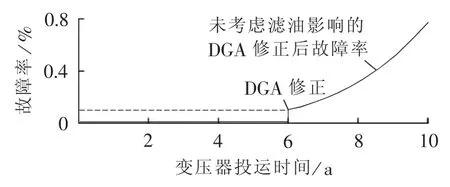
图9 没有考虑滤油影响的变压器故障率曲线Fig.9 Failure rate curve of transformer without influence of oil separation
经过检修之后,变压器内部绝缘故障得到及时处理,系统运行条件改善,预期寿命损失量减少,得到实际的寿命修正值 Z″,计算结果为:Z″=Zeq+χiZ′eq=23.016+0.5×41.10=43.57 (a)。
由HST和预期寿命对应曲线可得到变压器等效HST为71.50℃,得到变压器在滤油之后的故障率曲线如图10所示。
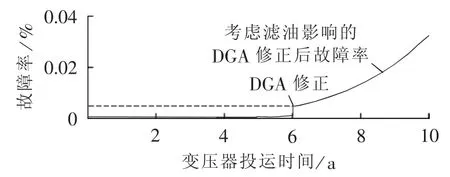
图10 考虑滤油影响后的变压器故障率曲线Fig.10 Failure rate curve of transformer with influence of oil separation
考虑滤油影响后,变压器运行到第6年的故障率为0.005%,远低于修正前的0.1%,同样的方法可得到变压器在实施涉及油纸绝缘系统的检修后的故障率修正值。
将变压器基础故障率曲线和加入动态修正后的曲线作对比分析,如图11和图12所示。

图11 变压器原始故障率曲线Fig.11 Original failure rate curve of transformer

图12 变压器实际的故障率曲线Fig.12 Actual failure rate curve of transformer
未加入修正的变压器故障率曲线是一条近似指数分布的静态曲线,在一定程度上能反映变压器的故障率随投运时间的变化关系;加入修正后的故障率曲线是一条类似阶梯状的分段曲线,变压器的故障率会随着变压器所经历的运行情况做出更新,是一条动态的可靠性评估曲线。
4 结论
本文首次将动态修正的概念引入变压器可靠性评估中,为变压器可靠性评估提供了新途径,经过大量的实验分析,该方法具有较强的有效性,从本文的研究结果可以得到以下结论:
a.模型的建立没有采用传统可靠性模型对面不对点的评估模式,使评估结果能够很好地兼顾变压器的个体差异性,结果更可靠;
b.模型采用基础模型加动态修正模型的结构,动态修正的加入使得整个可靠性评估模型能够根据评估对象的运行状态做出调整,可信度更高;
c.选择DGA数据作为动态修正的信息来源,并基于灰色理论进行处理,能较准确地诊断出变压器内部故障,确保评估值能很好地跟踪并反映变压器实际运行状态。
[1]李如琦,唐林权,凌武能,等.基于云理论和前景理论的变压器状态维修风险决策[J]. 电力自动化设备,2013,33(2):104-108.LI Ruqi,TANG Linquan,LING Wuneng,et al.Risk decisionmaking based on cloud theory and prospect theory for conditional maintenance of power transformer[J].Electric Power Automation Equipment,2013,33(2):104-108.
[2]徐岩,陈昕.基于合作博弈和云模型的变压器状态评估方法[J].电力自动化设备,2015,35(3):88-93.XU Yan,CHEN Xin.Transformer status assessment based on cooperative game and cloud model[J].Electric Power Automation Equipment,2015,35(3):88-93.
[3]杨洋,谢开贵,孙鑫.基于FTA法的宁夏电网运行元件故障率分析[J]. 电力系统保护与控制,2009,37(18):134-137,141.YANG Yang,XIE Kaigui,SUN Xin.Operating component failure rate analysis based on FTA for power system[J].Power System Protection and Control,2009,37(18):134-137,141.
[4]高明,李文云,袁德君,等.使用故障树理论对电网调度自动化系统应急预案完备度的量化分析[J].电力系统保护与控制,2010,38(17):58-63,69.GAO Ming,LI Wenyun,YUAN Dejun,et al.Completeness degree quantitative analysis of dispaching automation system emer-gency preplan based on FTA[J].Power System Protection and Control,2010,38(17):58-63,69.
[5]廖瑞金,肖中男,巩晶,等.应用马尔科夫模型评估电力变压器可靠性[J]. 高电压技术,2010,36(2):322-328.LIAO Ruijin,XIAO Zhongnan,GONG Jing,et al.Markov model for reliability assessment of power transformers[J].High Voltage Engineering,2010,36(2):322-328.
[6]郑君亮,江修波,蔡金锭.变压器油纸绝缘等效电路参数辨识及绝缘状态对参数的影响分析[J]. 电力自动化设备,2015,35(8):168-172.ZHENG Junliang,JIANG Xiubo,CAI Jinding.Parameter identification for equivalent circuit of transformer oil-paper insulation and effect of insulation condition on parameters[J].Electric Power Automation Equipment,2015,35(8):168-172.
[7]王有元,袁园,李剑,等.变压器油纸绝缘可靠性的威布尔混合评估模型[J]. 高电压技术,2010,36(4):842-848.WANG Youyuan,YUAN Yuan,LI Jian,et al.Weibull mixed evaluation model for reliability of oil-paper insulation in transformer[J].High Voltage Engineering,2010,36(4):842-848.
[8]MCNUTT W J. Insulation thermal life considerations for transformer loading guides[J].IEEE Trans on Power Delivery,1992,7(1):392-401.
[9]IEEE Working Group for Loading Mineral-Oil-Immersed Transformers.IEEE guide for loading mineral-oil-immersed transformers and step-voltage regulators:IEEE C57.91-2011 [EB /OL].[2015-12-10].http:∥standards.ieee.org /findstds/standard /C57.91-2011.htm l.
[10]毛一之,王秀春,韩鹏.应用绕组测量装置测量变压器绕组温度的必要性和可行性分析[J]. 变压器,2004,41(9):13-17.MAO Yizhi,WANG Xiuchun,HAN Peng.Analysis of fesibility and necessity to measure transformer wingding temperature by winding thermometric device[J].Transformer,2004,41(9):13-17.
[11]江淘莎.基于底层油温的油浸式变压器热点评估方法研究[D].重庆:重庆大学,2009.JIANG Taosha.Study on estimating method of hottest spot temperature in oil-immersed transformers[D].Chongqing:Chongqing University,2009.
[12]孙鹏,陈绍辉,张彩庆.基于Marquardt法参数估计的变电设备寿命周期故障率评估[J]. 电力系统保护与控制,2012,40(1):85-90.SUN Peng,CHEN Shaohui,ZHANG Caiqing.Assessment of failure rate for substation equipment life cycle based on Marquardt parameter estimation method [J].Power System Protection and Control,2012,40(1):85-90.
[13]AWADALLAH S K E,MILANOVIC J V,JARMAN P N.The influence of modeling transformer age related failures on system reliability[J].IEEE Trans on Power Systems,2015,30(2):970-979.
[14]LI W.Evaluating mean life of power system equipment with limited end-of-life failure data[J].IEEE Trans on Power Systems,2004,19(1):236-242.
[15]CHIODO E,MAZZANTI G.Bayesian reliability estimation based on a Weibull stress-strength model for aged power system components subjected to voltage surges[J].IEEE Trans on Dielectrics and Electrical Insulation,2006,13(4):935-937.
[16]FU W,MCCALLEY J D,VITTAL V.Risk assessment for transformer loading[J].IEEE Trans on Power Systems,2001,16(3):346-353.
[17]赵文清.基于选择性贝叶斯分类器的变压器故障诊断[J].电力自动化设备,2011,31(2):44-47.ZHAO Wenqing.Transformer fault diagnosis based on selective Bayes classifier[J].Electric Power Automation Equipment,2011,31(2):44-47.
[18]刘从法,罗日成,雷春燕,等.基于AHP灰色定权聚类的电力变压器状态评估[J]. 电力自动化设备,2013,33(6):104-107,133.LIU Congfa,LUO Richeng,LEI Chunyan,et al.Power transformer condition assessment based on AHP grey fixed-weight clustering [J].Electric Power Automation Equipment,2013,33(6):104-107,133.
[19]杨廷方,张航,黄立滨,等.基于改进型主成分分析的电力变 压器潜伏性故障诊断[J]. 电力自动化设备,2015,35(6):149-153,165.YANG Tingfang,ZHANG Hang,HUANG Libin,et al.Incipient fault diagnosis based on improved principal component analysis for power transformer[J].Electric Power Automation Equipment,2015,35(6):149-153,165.
[20]郑蕊蕊,赵继印,吴宝春,等.基于加权灰靶理论的电力变压器绝缘状态分级评估方法[J]. 电工技术学报,2008,23(8):60-66.ZHENG Ruirui,ZHAO Jiyin,WU Baochun,et al.Method for insulative condition classification evaluation of power transformer based on weight coefficient grey target theory [J].Transactions of China Electrotechnical Society,2008,23 (8):60-66.
[21]李建坡.基于油中溶解气体分析的电力变压器故障诊断技术的研究[D]. 长春:吉林大学,2008.LI Jianpo. Study on power transformer fault diagnosis technology based on dissolved gases analysis[D].Changchun:Jilin University,2008.
[22]李俭,孙才新,陈伟根,等.基于灰色聚类分析的充油电力变压器绝缘故障诊断的研究[J]. 电工技术学报,2002,17(4):80-84.LI Jian,SUN Caixin,CHEN Weigen,et al.Study on fault diagnosis of insulation of oil-immersed transformer based on grey cluster theory[J].Transactions of China Electrotechnical Society,2002,17(4):80-84.
[23]王谦.基于模糊理论的电力变压器运行状态综合评估方法研究[D]. 重庆:重庆大学,2005.WANG Qian.Study of the comprehensive assessment method for the power transformer condition in service with fuzzy theory[D].Chongqing:Chongqing University,2005.
[24]张镱仪,廖瑞金,杨丽君,等.基于云理论的电力变压器绝缘状态评估方法[J]. 电工技术学报,2012,27(5):13-19.ZHANG Yiyi,LIAO Ruijin,YANG Lijun,et al.An assessment method for insulation condition of power transformer based upon cloud model[J].Transactions of China Electrotecnical Society, 2012,27(5):13-19.
[25]韩帮军,范秀敏,马登哲.有限时间区间预防性维修策略的优化[J]. 上海交通大学学报,2003,37(5):679-682.HAN Bangjun,FAN Xiumin,MA Dengzhe.Optimal policy research of preventive maintenance in finite time horizon [J].Journal of Shanghai Jiaotong University,2003,37(5):679-682.
[26]潘乐真,张焰,俞国勤,等.状态检修决策中的电气设备故障率推算[J]. 电力自动化设备,2010,30(2):91-94.PAN Lezhen,ZHANG Yan,YU Guoqin,et al.Prediction of electrical equipment failure rate for condition-based maintenance decision-making[J].Electric Power Automation Equipment,2010,30(2):91-94.

