深度研究考题 有效应对高考——近年来新课标全国卷Ⅰ(理科)的考题分析及2016年高考命题展望

合肥工业大学附中　　余树宝　　(邮编：230009)



复习考试

深度研究考题有效应对高考
——近年来新课标全国卷Ⅰ(理科)的考题分析及2016年高考命题展望

合肥工业大学附中余树宝(邮编：230009)

2016年高考在即，在为数不多的时间里，如何做到有效复习，有针对性地应对2016年高考，笔者在认真研究近年来高考试题的基础上，做了一些思考，希望能为同行提供一点参考．

1全国课标卷的特点

全国卷的试题基本遵循“稳中有变、立足基础、突出能力、锐意求新”的命题指导思想，突出“三基”，坚持重点知识、重要思想、重要能力的考查，坚持通性通法的考查，难度适中，有较好的区分度，回避偏、难、怪的试题．具体来说，淡化技巧，考查基础；形式灵活，考查能力；回归课本，适度创新；融入传统，呈现特色．

稳定应该是全国卷最大的特点，体现在：一是试卷结构上的稳定，全国卷共22题，其中12道选择题(每题5分)、4道填空题(每题5分)、6

道解答题(前5题每题12分，最后一题为三选一，10分)；二是试题考查内容上的稳定，有规律地看出选择、填空题考点的分布稳定，解答题的考点也相对稳定，第17题考数列或三角，第18、19题考查统计与概率、立体几何，第20题考查解析几何，第21题考查函数与导数，最后一题考生可从第22题“几何证明选讲”、第23题“坐标系与参数方程”、第24题“不等式选讲”三题中任选一题作答；三是难度上稳定，区别各省市自主命题，学生见到全国卷不会感觉陌生、更不会感到害怕，基本功扎实的同学能拿到大部分的分数．

2考点分布

下面是2011～2015年各主干知识的考题分布及分值：

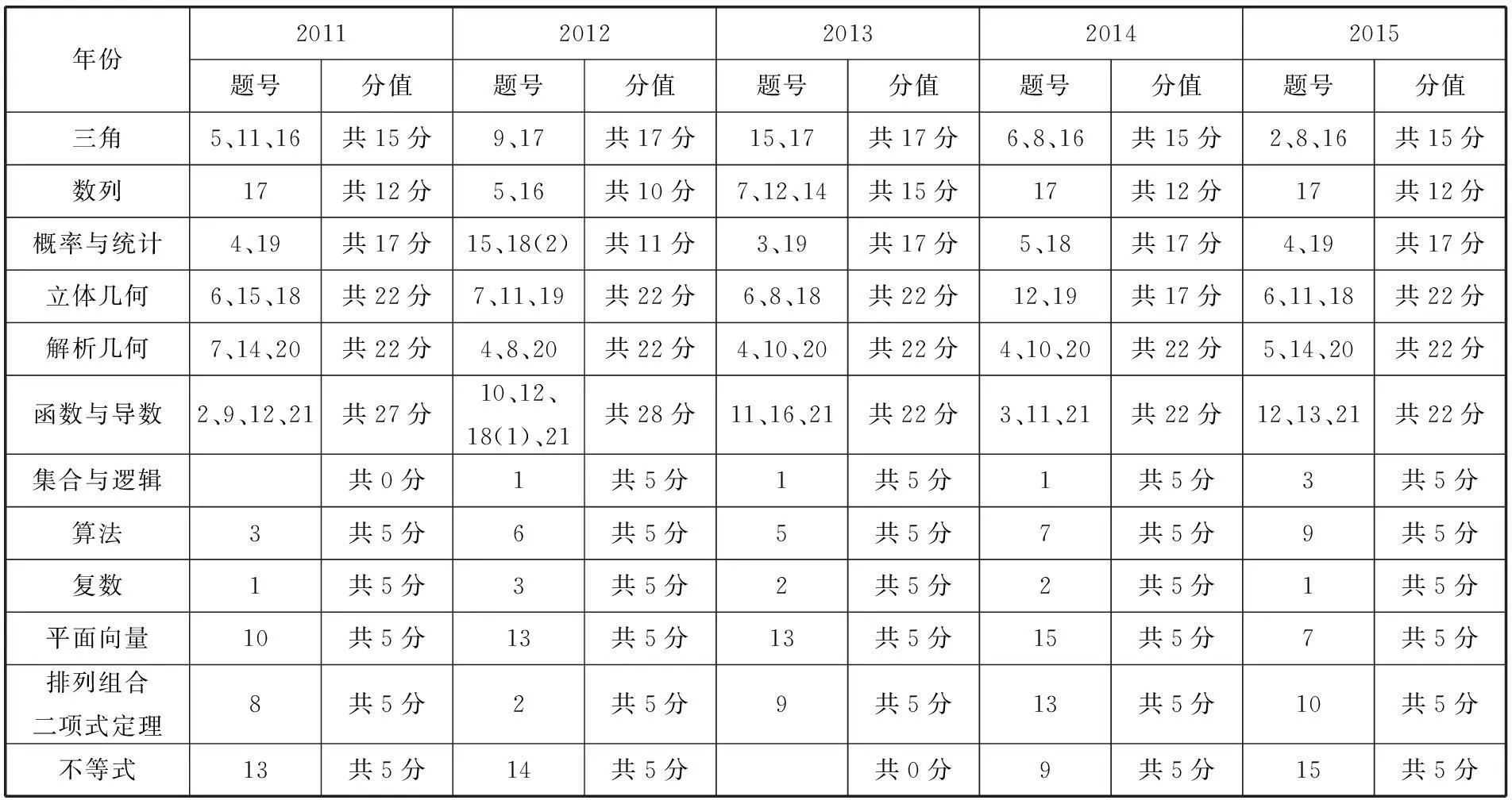
年份20112012201320142015题号分值题号分值题号分值题号分值题号分值三角5、11、16共15分9、17共17分15、17共17分6、8、16共15分2、8、16共15分数列17共12分5、16共10分7、12、14共15分17共12分17共12分概率与统计4、19共17分15、18(2)共11分3、19共17分5、18共17分4、19共17分立体几何6、15、18共22分7、11、19共22分6、8、18共22分12、19共17分6、11、18共22分解析几何7、14、20共22分4、8、20共22分4、10、20共22分4、10、20共22分5、14、20共22分函数与导数2、9、12、21共27分10、12、18(1)、21共28分11、16、21共22分3、11、21共22分12、13、21共22分集合与逻辑共0分1共5分1共5分1共5分3共5分算法3共5分6共5分5共5分7共5分9共5分复数1共5分3共5分2共5分2共5分1共5分平面向量10共5分13共5分13共5分15共5分7共5分排列组合二项式定理8共5分2共5分9共5分13共5分10共5分不等式13共5分14共5分共0分9共5分15共5分

从上表中不难看出函数与导数、解析几何、立体几何、概率与统计、三角函数与解三角形、数列等高中数学主干知识是高考考查的重要内容，总分值约为110分，约占高考总分的73%．

3选择题与填空题的重要考点

下表是2012～2015年选择题与填空题的考点分布：

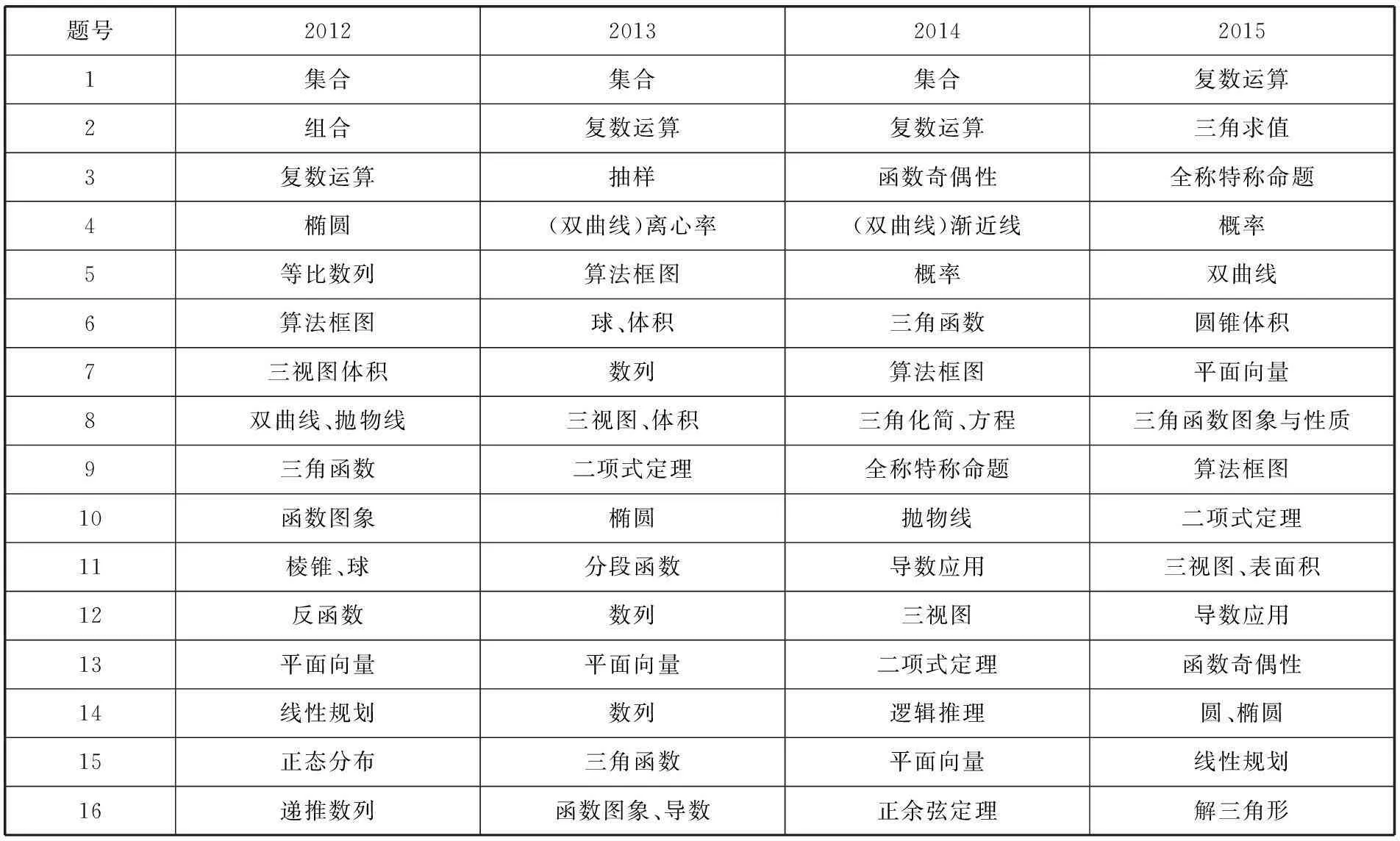
题号20122013201420151集合集合集合复数运算2组合复数运算复数运算三角求值3复数运算抽样函数奇偶性全称特称命题4椭圆(双曲线)离心率(双曲线)渐近线概率5等比数列算法框图概率双曲线6算法框图球、体积三角函数圆锥体积7三视图体积数列算法框图平面向量8双曲线、抛物线三视图、体积三角化简、方程三角函数图象与性质9三角函数二项式定理全称特称命题算法框图10函数图象椭圆抛物线二项式定理11棱锥、球分段函数导数应用三视图、表面积12反函数数列三视图导数应用13平面向量平面向量二项式定理函数奇偶性14线性规划数列逻辑推理圆、椭圆15正态分布三角函数平面向量线性规划16递推数列函数图象、导数正余弦定理解三角形

从上表中可以看出历年高考选择、填空题必考考点或频考考点是：集合的基本运算、常用逻辑用语、复数运算、程序框图、三视图及表面积或体积运算、线性规划、平面向量运算、等差或等比数列基本运算、三角求值、三角函数图象与性质、解三角形、二项式定理、直线与圆、圆锥曲线的性质、函数的图象与性质、函数的零点与方程的根等．

4解答题的重要考点

4.1必考内容

下表是2011～2015年解答题的考点分布：

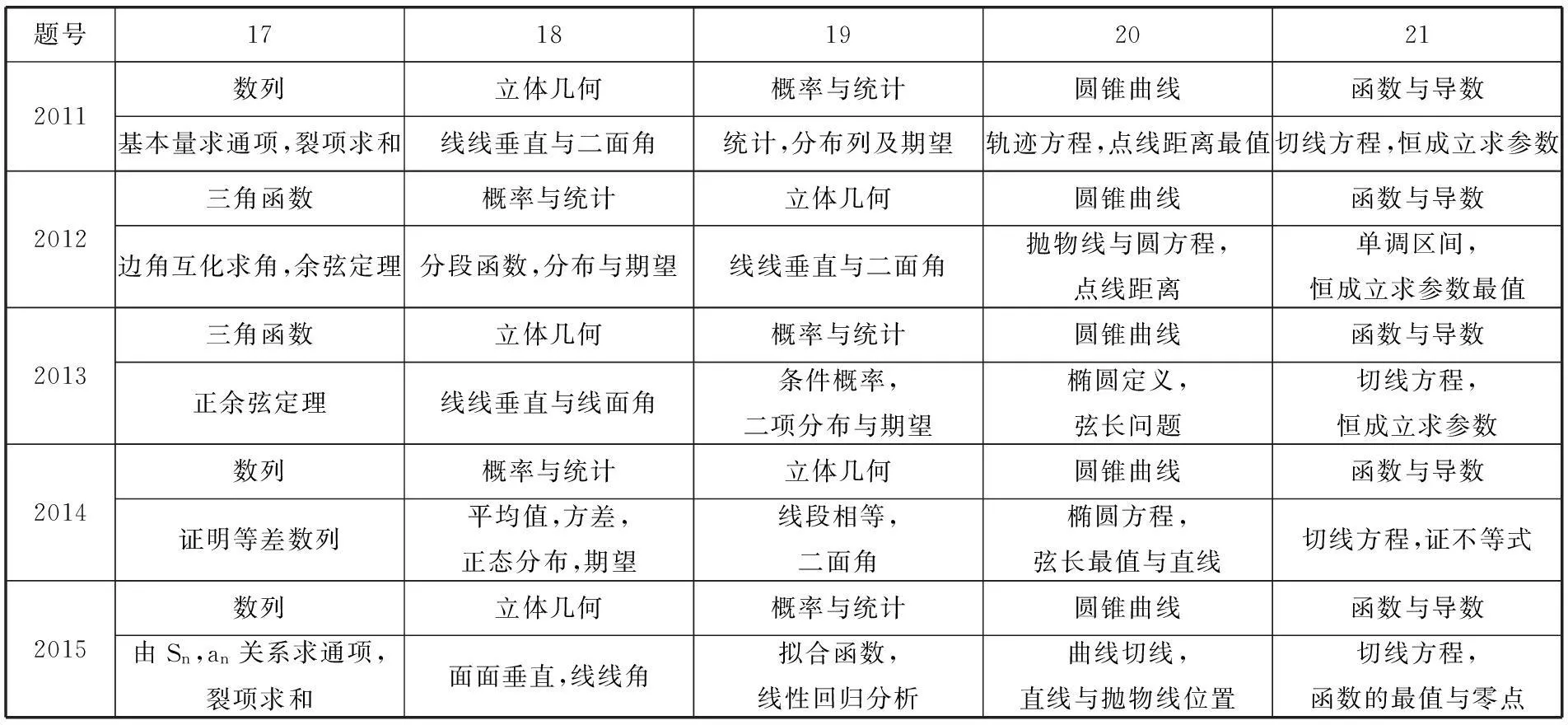
题号17181920212011数列立体几何概率与统计圆锥曲线函数与导数基本量求通项,裂项求和线线垂直与二面角统计,分布列及期望轨迹方程,点线距离最值切线方程,恒成立求参数2012三角函数概率与统计立体几何圆锥曲线函数与导数边角互化求角,余弦定理分段函数,分布与期望线线垂直与二面角抛物线与圆方程,点线距离单调区间,恒成立求参数最值2013三角函数立体几何概率与统计圆锥曲线函数与导数正余弦定理线线垂直与线面角条件概率,二项分布与期望椭圆定义,弦长问题切线方程,恒成立求参数2014数列概率与统计立体几何圆锥曲线函数与导数证明等差数列平均值,方差,正态分布,期望线段相等,二面角椭圆方程,弦长最值与直线切线方程,证不等式2015数列立体几何概率与统计圆锥曲线函数与导数由Sn,an关系求通项,裂项求和面面垂直,线线角拟合函数,线性回归分析曲线切线,直线与抛物线位置切线方程,函数的最值与零点

从上表中可以看出，第17题呈现两年三角、两年数列的特点，第18、19题为立体几何、概率与统计交替出现的情形，第20题考查圆锥曲线，第21题考查函数与导数．

下面就2016年高考解答题的考查方向，做一个建议性的展望.

4.1.1三角函数与解三角形

(1)纵观历年考题，发现规律，估计今年解答题第1题(第17题)很大可能考 “三角”；

(2)重点考查解三角形问题，能够熟练运用正弦定理、余弦定理、面积公式等知识和方法解决问题．一般问题形式为三个条件求值，两个条件求范围．解题过程中特别注意“角”的有界性；

(3)考查三角函数图象与性质问题．正确运用“四大公式”化简三角函数解析式，会解决形如y=Asin(ωx+φ)的周期性、单调性等性质问题；

(4)考查正、余弦定理在解决测量和几何计算有关的实际应用问题．新课程最大亮点就是体现了数学内容在解决实际问题中的应用．

4.1.2数列

(1)很大可能不在解答题中考查数列知识，选择、填空题会出现两小题，一道考查等差或等比数列的基本运算，一道考查由递推关系式求通项或一般数列的求和；

(2)降低难度，少与其它知识综合，单纯考查数列求值或性质(单调性、周期性)问题，淡化数学归纳法；

(3)重点考查两个简单数列(等差、等比)的基本运算问题，解题过程中抓住两个关键量a1,d(q),依据通项公式、求和公式建立方程组，适时巧用数列的性质；

(4)会用累加法、累积法、构造法等方法由简单的递推关系式求通项公式；会用裂项法、错位法、分组法等方法求非等差(等比)数列的前n项和．

4.1.3概率与统计

(1)重点考查离散型随机变量的分布列与期望；考查古典概型、几何概型、互斥事件有一个发生的概率、条件概率、相互独立事件同时发生的概率、n次独立重复试验及二项分布、超几何分布、正态分布等；

(2)考查统计问题，如五个样本频率分布图表(频率分布表、频率分布直方图、条形图、折线图、茎叶图)、四个数字特征(众数、中位数、平均数、方差与标准差)、三种抽样(简单随机抽样、系统抽样、分层抽样)、、两个分析(独立性检验、回归分析)等；

(3)试题多以概率与统计综合考查的形式出现，这也是全国卷的特点．突出考查数据处理能力、应用意识和统计思想，试题综合性强、阅读量大；

4.1.4立体几何

(1)重点考查空间几何体中线、面垂直与平行的论证问题；

(2)重点考查空间角问题．会用空间向量的方法求线线角、线面角、面面角；会求距离、求体积；

(3)试题形式一般是第一问是平行或垂直的证明问题(尤其是垂直证明)；第二问是空间角的计算，估计2016年可能会考线面角．

4.1.5解析几何

(1)会求确定类型的曲线方程(主要是椭圆或抛物线)或求动点的轨迹方程，用定义法、待定系数法、直接法、相关点法、参数法来求解；

(2)重点考查直线与圆锥曲线(椭圆或抛物线或圆)、点与圆锥曲线的关系下的问题，例如弦长、中点、轨迹、圆锥曲线中的三角形等．灵活运用圆锥曲线的定义、性质、弦长公式、点差法来解题，会用韦达定理，采取设点而不求、整体代入的思想来解题；

(3)会求与曲线有关的定点、定值、最值、存在性、探究性等问题，学会用参数方程来解决，注意平面向量与解析几何知识的综合；

(4)试题形式一般是两问：第一问以求曲线方程为主；第二问考查直线与圆锥曲线的位置关系．

4.1.6函数与导数

(1)在压轴题位置，难度较大；

(2)重点考查导数的几何意义，会由曲线的切线方程求解解析式中参数的值；

(3)重点考查利用导数研究指数函数(y=ex)或对数函数(y=lnx)与多项式函数复合而成的函数的单调性、最值、零点等问题，会用参变量分离、构造函数、数形结合等方法来解决不等式恒成立、不等式证明、方程的根等问题；尤其是有时需要对导函数进行深入分析，通过二阶导函数值的符号来研究一阶导数值范围，难度较大，要求较高；

(4)考查分类讨论思想、化归与转化思想、数形结合思想、函数与方程思想．

4.2选考内容

下表是2011～2015年选考题的考点分布：

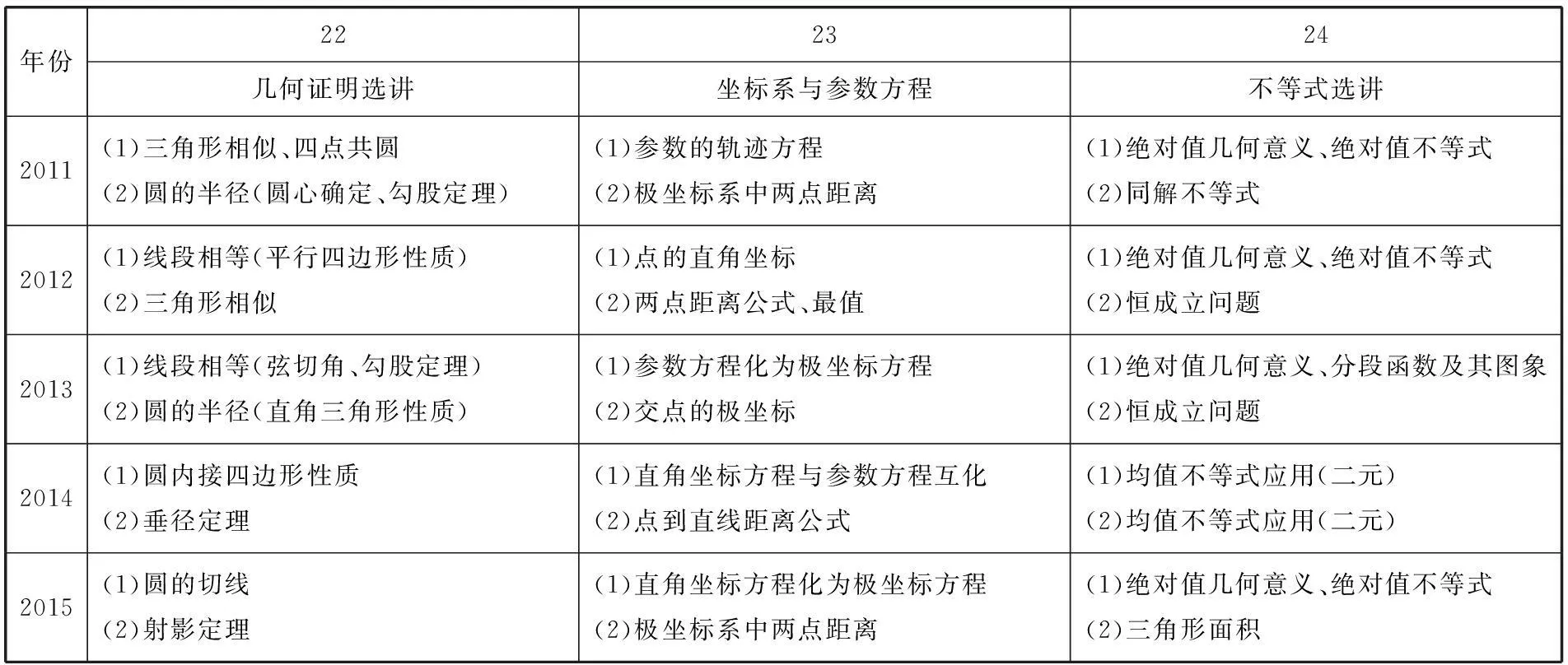
年份222324几何证明选讲坐标系与参数方程不等式选讲2011(1)三角形相似、四点共圆(2)圆的半径(圆心确定、勾股定理)(1)参数的轨迹方程(2)极坐标系中两点距离(1)绝对值几何意义、绝对值不等式(2)同解不等式2012(1)线段相等(平行四边形性质)(2)三角形相似(1)点的直角坐标(2)两点距离公式、最值(1)绝对值几何意义、绝对值不等式(2)恒成立问题2013(1)线段相等(弦切角、勾股定理)(2)圆的半径(直角三角形性质)(1)参数方程化为极坐标方程(2)交点的极坐标(1)绝对值几何意义、分段函数及其图象(2)恒成立问题2014(1)圆内接四边形性质(2)垂径定理(1)直角坐标方程与参数方程互化(2)点到直线距离公式(1)均值不等式应用(二元)(2)均值不等式应用(二元)2015(1)圆的切线(2)射影定理(1)直角坐标方程化为极坐标方程(2)极坐标系中两点距离(1)绝对值几何意义、绝对值不等式(2)三角形面积

4.2.1几何证明选讲

(1)几何证明主要考查三角形相似，圆的切割线定理，证明成比例，基本定位在圆与多边形的切接问题；

(2)求角度，求长度；

(3)利用射影定理解决圆中计算(长度、角度、面积等)和证明(线段成比例、四点共圆等)问题是历年高考题的热点.

4.2.2坐标系与参数方程

(1)会进行参数方程与普通方程的互化，会进行极坐标方程与直角坐标方程的互化；

(2)会利用参数方程、极坐标方程求解曲线的基本量；

(3)一般考题会以直线与圆(椭圆)位置关系为背景，考查方程互化、坐标互化、交点坐标、轨迹方程、距离、面积、最值等；

(4)由于此题与解析几何相关知识联系紧密，建议指导考生把此题作为三选一的首选试题．

4.2.3不等式选讲

(1)会解绝对值不等式，会解含有参变数的关于x的不等式；

(2)求解不等式恒成立时参变数的取值范围；

(3)会用均值定理、放缩法等方法证明不等式．

以上就是我对全国卷的考题分析，研究得不深，理解得不透，仅供同行们参考，不妥之处，请各位批评指正．不过无论我们怎么预测，我们在复习的过程中都不能把宝压在一类题型之中，应对高考不是赌博，不能靠“押题、猜题”，所以真正的厚积薄发才是王道，知己知彼，扎实积累才是我们高考取胜的关键．

(收稿日期：2016-02-20)