多维地震激励下人字形桥梁地震模拟振动台试验研究

闫　磊， 李青宁， 尹俊红， 韩　春， 程麦理

(西安建筑科技大学 土木工程学院，西安　710055)



多维地震激励下人字形桥梁地震模拟振动台试验研究

闫磊， 李青宁， 尹俊红， 韩春， 程麦理

(西安建筑科技大学 土木工程学院，西安710055)

摘要：为研究人字形桥梁在地震作用下的动力响应，以某人字形桥梁为原型，制作了一座相似比为1∶20的模型桥梁，采用El-Centro波对其进行了不同地震烈度的多维激励地震模拟振动台试验和有限元分析。研究结果表明：随着地震烈度的增加，模型结构自振频率降低阻尼比增大；桥墩墩顶顺桥向加速度响应基本不受竖向地震分量影响；计算桥墩墩底应变响应时进行水平双向地震激励即可满足要求；梁体跨中竖向加速度响应，主梁和分支梁间的伸缩缝宽度取值，伸缩缝处的碰撞响应等均与地震波输入维度有关。因此，对于人字形桥梁在进行抗震设计时应针对不同的设计目的对其进行选择性的多维地震激励。

关键词：人字形桥梁；多维激励；振动台试验；有限元分析; 抗震设计

为适应地形、解决交通分流等问题，越来越多的非规则桥梁拔地而起，成为自然界一道道亮丽的风景线。人字形桥梁作为非规则桥梁的一种，一方面能够很好的解决立交中各交点的平曲线设计问题，另一方面也能解决交通量的分流问题，使不同走向的道路联系起来为行车带来极大的方便。在受力方面，人字形桥梁不仅具有薄壁直线箱梁和薄壁曲线箱梁两者的受力特点，而且包含了桥梁宽度变化、曲率变化等空间因素的影响。在地震作用下，人字形桥梁除产生拉、压、弯曲和剪力外，还将产生扭转、畸变等复杂受力状态。因此，研究地震作用下人字形桥梁的抗震性能显得尤为重要。振动台试验作为一种有效的再现地震过程的手段，目前已被广泛采用[1]。以往的桥梁结构振动台试验研究中，对规则桥梁已进行了较深入的研究[2-4]，然而对非规则桥梁则主要进行了一些拱桥和简单线形曲线桥梁的振动台试验研究[5-9]，这些试验主要对非规则桥梁进行了单向的地震模拟振动台试验，对非规则桥梁进行多维激励的振动台试验目前还少有研究。对于人字形桥梁结构，目前主要进行了模型的静力试验和数值分析[10-11]。基于此，本文以某人字形桥梁为原型，制作了一座相似比为1∶20的人字形模型桥梁，对该结构进行多维地震输入下的地震模拟振动台试验，研究了该结构在多维地震输入下的动力响应。通过本文研究，以期为我国人字形桥梁的抗震研究提供试验依据。

1试验设计

1.1相似比设计

振动台试验中难以完全满足所有参数完全相似，一般情况下，满足主要参量的相似比即可[12]。本文以长度、密度、弹模作为基本物理量，推导出其它主要相似常数见表1。

表1　相似常数

1.2模型材料

振动台试验中，模型材料选取是否正确直接影响着试验结果的可视性及准确性。由于微粒混凝土可达到相同混凝土强度，弹性模量较普通混凝土小，适宜于比例缩尺结构的振动台试验[13]，故模型材料中混凝土选用自行研制配合比的微粒混凝土，图1为微粒混凝土参数的测试过程。经测试，微粒混凝土MC25弹性模量为2.2×104N/mm2，通过相似比换算，完全可以模拟实际桥梁结构的普通混凝土C50。

模型桥墩纵筋均采用Φ8 mm的HRB335级带肋钢筋，箱梁纵筋均采用Φ6 mm的HRB335级带肋钢筋，全桥箍筋均采用Φ6 mm HPB300级光圆钢筋，箍筋间距均按6 cm设计，箱梁空心部分采用轻质泡沫板作为内模，箱梁和桥墩钢筋骨架(见图2)。

模型在1#、3#、5#墩上设置固定支座，其余自由墩墩顶处设置2个普通板式橡胶支座，固定支座尺寸9 cm×9 cm×1.5 cm，普通板式橡胶支座为6 cm×6 cm×1.5 cm。固定支座使用普通板式橡胶支座内置钢柱模拟。经试验测得固定支座水平剪切刚度为kx=ky=3.81×106N/m，竖向刚度为kz=7.11×107N/m，普通板式橡胶支座的水平剪切刚度kx=ky=2.88×105N/m，竖向刚度kz=5.61×107N/m，满足试验要求。模型支座见图3。

为模拟并实测伸缩缝处的碰撞响应，在模型桥梁1#、2#伸缩缝处设置了如图4所示的碰撞装置，碰撞初始间隙按5 mm设置。通过测量钢柱与钢板碰撞后钢柱上产生的应变来实测模型桥伸缩缝处的碰撞响应。

图1　微粒混凝土参数测定Fig.1 Particle concrete parameters determination

图2　钢筋骨架Fig.2 Framework of steel reinforcement

图3　模型支座Fig.3 Bearings of model

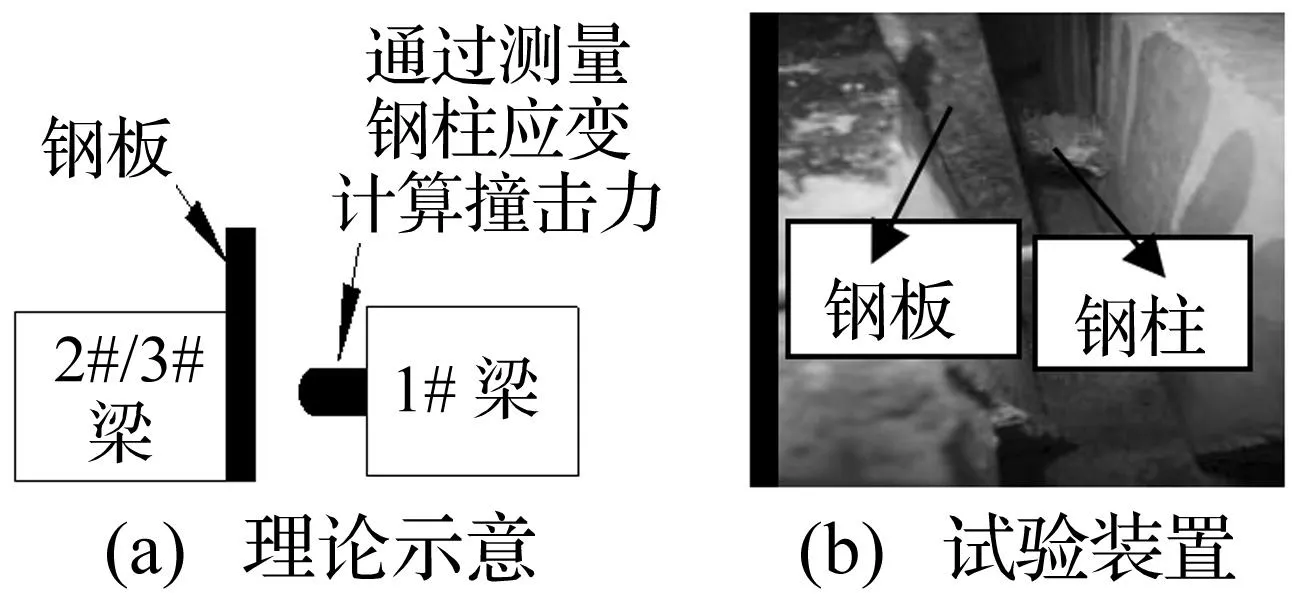
图4　碰撞装置Fig.4 Poundingdevice

1.3模型设计

模型桥梁中1#主梁为单箱双室异形梁， 1#墩处桥面宽70 cm，2#墩处桥面宽88 cm。2#分支直梁为单箱单室截面，桥面宽44 cm。3#分支曲梁为单箱单室截面，桥面宽44 cm。模型桥墩均为矩形实心截面，采用同一尺寸进行设计，桥墩高150 cm，底座高30 cm，所有墩均采用现浇施工与基座连接。基座与振动台台面通过螺栓可靠连接。模型结构在振动台上安装时以东西向(分支直梁顺桥梁)为X方向，垂直于X方向为Y方向，垂直于XY平面为Z方向。模型设计后的平面及主要截面配筋情况见图5。

图5　模型设计(单位：cm)Fig.5 Model design(units:cm)

1.4模型配重

振动台缩尺比例试验中，模型结构须通过配重来满足动力质量相似[14-15]。本试验在梁体表面配重箱内施加配重，采用质量为5 kg的规则金属块均匀布置于各配重箱中，1#梁施加配重1 275 kg，2#梁施加配重555 kg，3#梁施加配重650 kg，总配重为2 480 kg。通过相似关系计算的模型理论配重为3 000 kg，实际配重与其相比，配重率达到80%以上，满足动力相似要求。配重完成后的结构见图6。

图6　模型配重Fig.6 Model weight

1.5测点布置

西安建筑科技大学地震模拟振动系统台面尺寸为 4.1 m×4.1 m，激振方向为X、Y、Z三方向，控制自由度为六自由度，台面最大有效荷载为22 t，台面载荷20 t时，水平向最大加速度可达1.5 g，竖向最大加速度可达1 g。因此，该系统完全能够满足本试验加载要求。试验过程中主要对该模型各测点的加速度、位移和应变响应进行测量。加速度传感器共布置12个，其中振动台台面3个方向各布置1个，6个桥墩墩顶顺桥向各布置1个，1#梁、2#梁顶跨中各布置1个竖向加速度计，3#梁西侧第一跨跨中布置1个竖向加速度计。位移传感器共布置7个，振动台台面3个方向各布置1个，1#梁顶东侧沿2#梁、3#梁方向各布置1个，2#梁顶西侧沿顺桥向布置1个，3#梁顶西侧沿顺桥向布置1个。应变测点共布置14个，每个桥墩底部沿主筋对角位置各布置1个，伸缩缝处碰撞钢柱上各布置1个。

2地震波及加载工况

2.1地震波选取

本文主要研究人字形桥梁结构位于Ⅱ类场地土时的动力响应，选取适合Ⅱ类场地土的El-Centro波(NS向和EW向)作为输入地震波，归一化地震波及频谱曲线(见图7)。试验地震波以东西向为X方向，垂直于X方向为Y方向，垂直于XY平面为Z方向。原型地震波加速度峰值采用7 度0.1 g，8度0.2 g，8度0.3 g，9度0.4 g。根据相似关系，振动台台面实际输入地震波峰值分别调整为0.250 g、0.500 g、0.750 g、1.000 g。

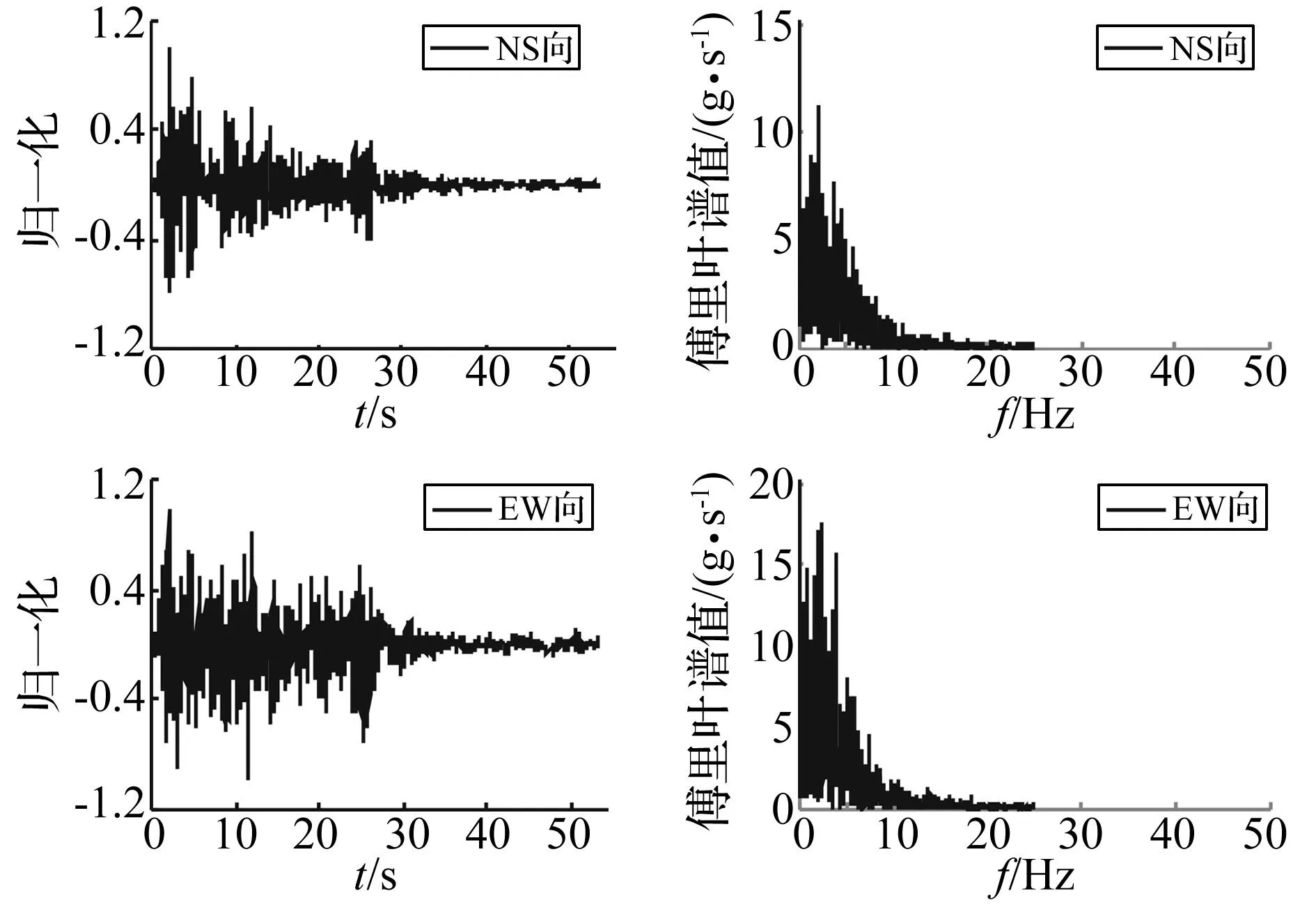
图7　试验用波Fig.7 Earthquake waves for test

2.2试验工况

本试验采用三种激励方式：单向X激励，双向XY激励，三向XYZ激励。El-Centro 波(NS向)作为X和Z向的激励，EI-centro波(EW向)作为Y向激励。多维输入时，输入地震波峰值按X∶Y∶Z=1∶0.85∶0.65[16-17]。试验在每级加载前后均进行白噪声扫描，用以反应结构不同加载阶段的动力特性。表2为模型结构试验工况台面理论及实测加速度峰值，由此可见，台面地震波输入烈度满足要求。

3试验结果

3.1动力特性

通过白噪声激励可测得人字形桥梁的加速度响应时程曲线，然后进行 FFT 变换和半功率带宽法可得到模型在不同地震烈度加载前后的动力特性见表3。

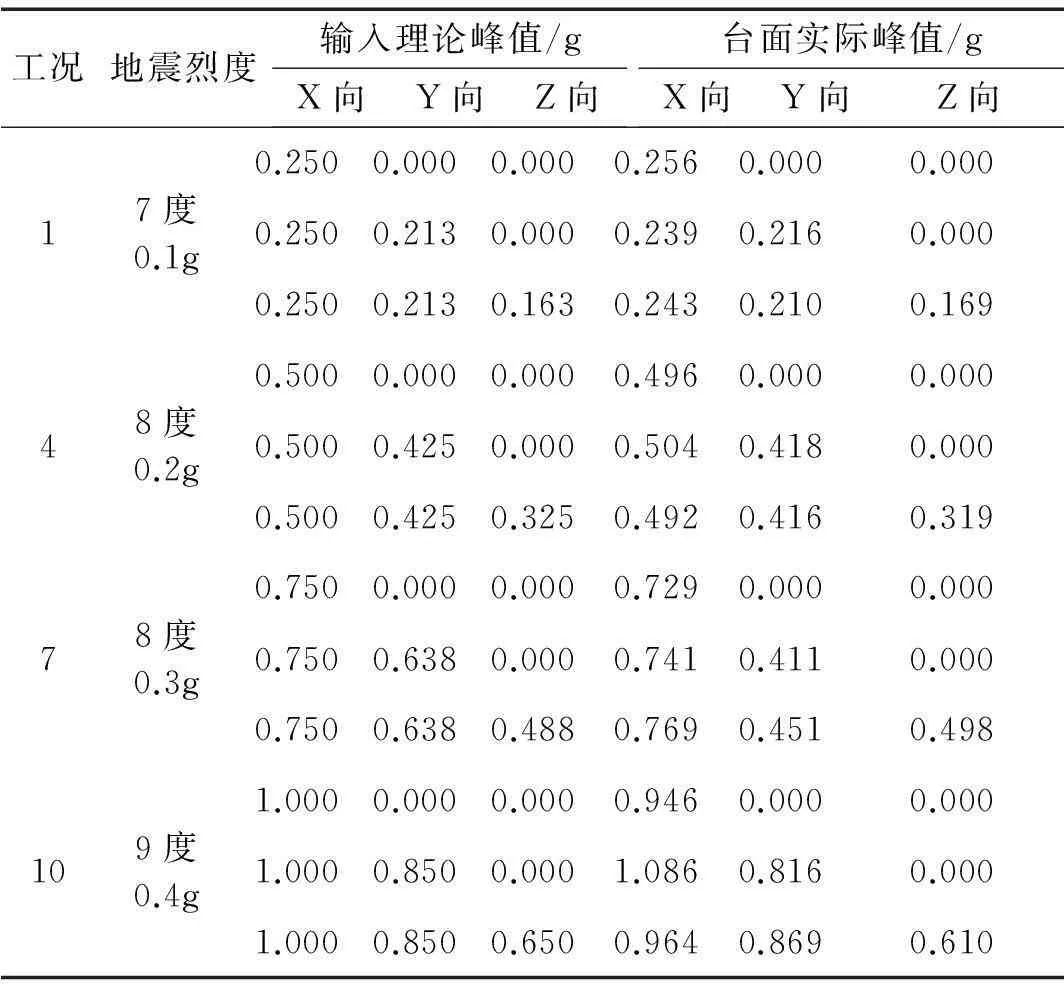
表2　试验工况

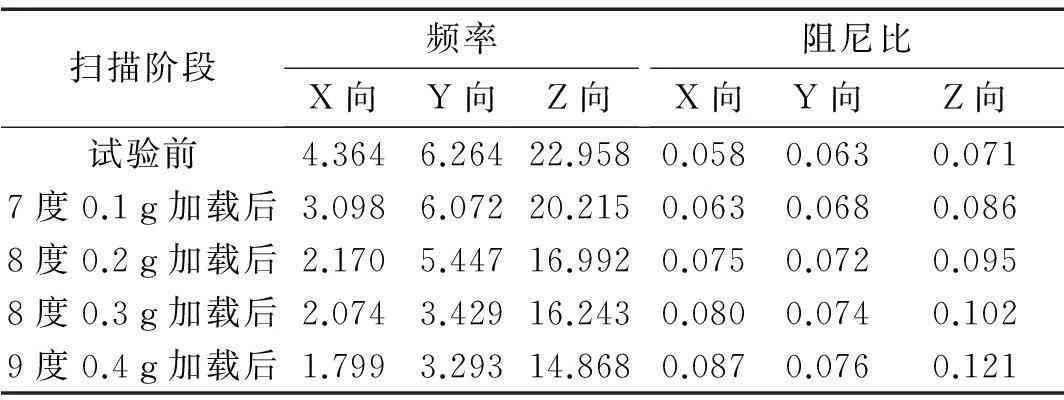
表3　模型结构动力特性

由表3可知，随着地震烈度的增加其不同方向的基频逐渐降低，阻尼比逐渐增大，说明整个试验过程中模型结构有损伤，刚度退化。模型结构试验前的基频Z向最大，Y向次之，X向最小；试验完成后模型结构X向频率降低率为58.8%，Y向频率降低率为47.4%,Z向频率降低率为35.2%,说明模型结构X向刚度较小，且刚度退化现象相比Y、Z向严重。

3.2加速度响应

3.2.1墩顶加速度响应分析

图8为模型结构在7度0.1 g时地震波沿X向输入时1#墩至6#墩墩顶顺桥向加速度响应时程曲线，限于篇幅原因其余工况时各测点的时程曲线图形未一一列出，表4给出不同工况下各测点的加速度峰值。

图8　墩顶顺桥向加速度时程曲线Fig.8 Acceleration time history curves of pier top in longitudinal

由表4可知：

(1) 地震波沿X向输入时，随着地震烈度的增加，各测点加速度响应逐渐增大。模型结构1#、2#、3#、4#墩墩顶顺桥向加速度峰值相比台面输入均有放大，其中9度0.4g输入时，3#墩墩顶顺桥向加速度相比台面放大了144.08%。5#、6#墩墩顶顺桥向加速度峰值相比台面均有减小，出现上述结果是因为当地震波沿X向输入时，1#、2#、3#、4#号墩与地震波方向正交(4#墩虽未正交但夹角较小，仅为6度)，其加速度响应沿桥墩高度方向将会放大，故墩顶加速度峰值相比台面放大；5#、6#墩为分支曲梁下部桥墩，与地震波输入方向斜交角度较大，故其顺桥向加速度峰值仅为X向的一个分量，因而墩顶加速度峰值相比台面有降低，且6#墩降低率大于5#墩。

表4　墩顶顺桥向加速度峰值(g)

(2) 地震波沿XY向输入时，对于与地震波输入方向正交的1#、2#、3#墩而言，其顶顺桥向加速度峰值相比X向输入基本无变化，但4#、5#、6#墩顶加速度峰值相比单向输入均有减小，且随着地震烈度的增加，减小幅度越大，9度0.4 g时5#墩顶峰值减小26.07%，6#墩顶峰值减小50.30%。

(3) 地震波沿XYZ三向输入时，墩顶各测点加速度响应峰值相比XY向输入基本无变化。

3.2.2梁跨中加速度响应分析

图9为地震烈度为8度0.2 g时X向地震输入时1#、2#梁跨中及3#梁西侧第1跨跨中竖向加速度时程曲线。限于篇幅原因其余时程曲线未在文中一一给出，仅在表5中列出不同工况下各测点的加速度峰值。

图9　跨中竖向加速度时程曲线Fig.9 Vertical acceleration time history curves of mid span

由表5可知：模型结构沿水平单向和双向输入时均会引起桥梁结构的竖向振动，且随着地震烈度的增加模型结构竖向振动越明显。同一地震烈度，模型桥梁梁顶竖向加速度峰值单向输入较双向输入小，双向输入较三向输入小。当地震烈度为9度0.4 g时，1#梁、2#梁、3#梁跨中三向和双向输入较单向输入增幅分别为1 748.3%、450.6%、1 916.8%、388.4%、1 623.8%、481.2%。上述结果说明：对于人字形桥梁，地震波沿X向输入时，会引起桥梁结构竖向的振动；当地震波沿两个水平正交方向输入时，会引起桥梁结构竖向振动的加强；竖向地震波对人字形桥梁梁体跨中竖向加速度的影响明显，且直梁部分更为显著。

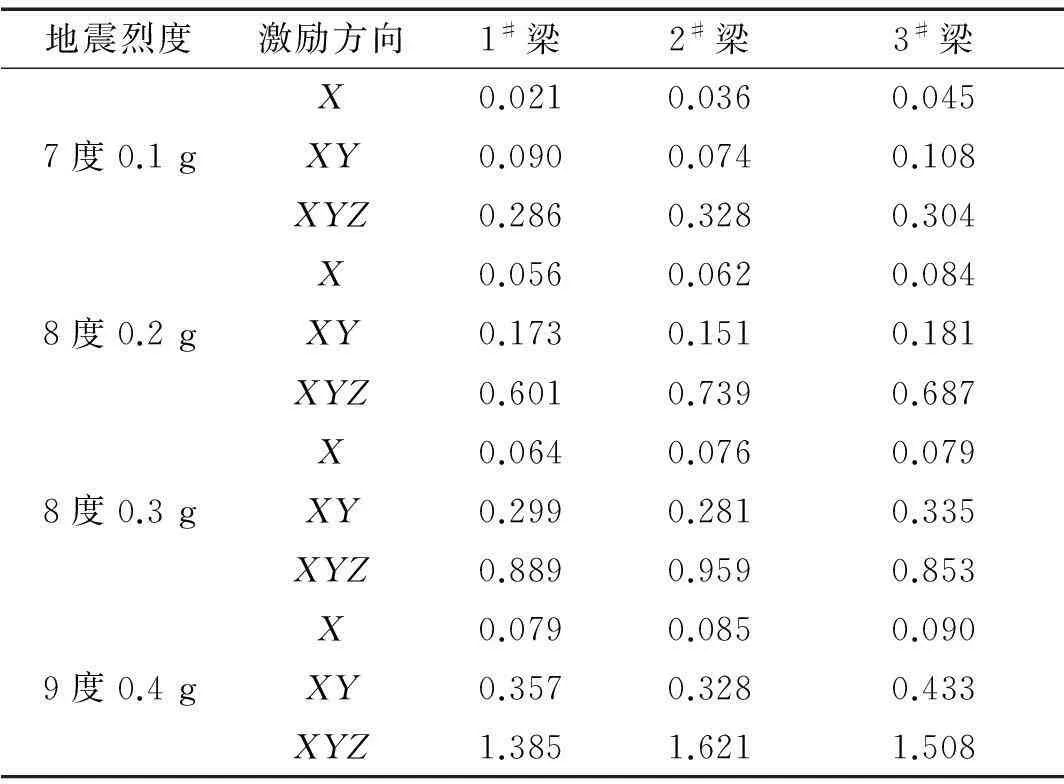
表5　梁跨中竖向加速度峰值(g)

比较分支直梁和分支曲梁梁体的竖向加速度响应，在单向和双向输入时，分支直梁的竖向加速度响应总是小于分支曲梁，但当竖向地震动与水平向同时作用时，分支直梁的竖向加速度响应大于分支曲梁。因此，人字形桥梁结构中，水平向地震动输入引起分支曲梁的竖向振动响应较分支直梁显著，竖向地震动输入对分支直梁的竖向振动响应较分支曲梁显著。

综上，人字形桥梁由于其不同跨的结构布置、质量分布以及对地震动的敏感带等参数的不同，导致其对于相同地震动作用时，其不同跨表现为不同的动力响应。实际人字形桥梁结构有竖向地震动输入时，将会引起桥梁结构竖向的强烈振动，有可能导致以下震害：① 竖向地震动引起固定支座处的抗拔力不足导致固定支座处的竖向破坏。② 竖向地震动引起梁体的竖向剧烈振动，从而引起桥墩截面应力的强烈变化，增加桥墩的竖向荷载效应，可能引起桥墩混凝土的压碎，甚至可能造成桥墩钢筋屈服。③ 竖向地震动会剧烈增加梁体的竖向振动，从而增加梁体的跨中弯矩需求，强震作用下，可能会使得梁体的受力超过其设计承载力，引起梁体竖向裂缝等震害的形成。不仅本试验的震害现象证明了这三点灾变现象，同时其也与以往的理论研究[18-19]不谋而合。

3.3位移响应分析

强烈地震作用下会引起桥梁结构相邻梁体间产生过大的相对位移，若邻梁相对位移大于结构伸缩缝的宽度，邻梁之间必然发生碰撞。为合理设置伸缩缝的宽度，本文研究了主梁与分支直梁和分支曲梁的相对位移。试验中在1#梁右端，2#和3#梁的左端布置了位移计，通过对主梁和分支梁的位移时程曲线进行实时做差并取峰值可计算出不同设防烈度下不同地震输入方向时伸缩缝的最小需求宽度。本文以地震设防烈度为8度0.3g为例来说明1#梁与2#梁和1#梁与3#梁在不同地震方向输入时人字形桥梁主梁与分支梁之间设置伸缩缝宽度的影响因素。8度0.3g时不同方向地震输入时的相对位移峰值见图10。

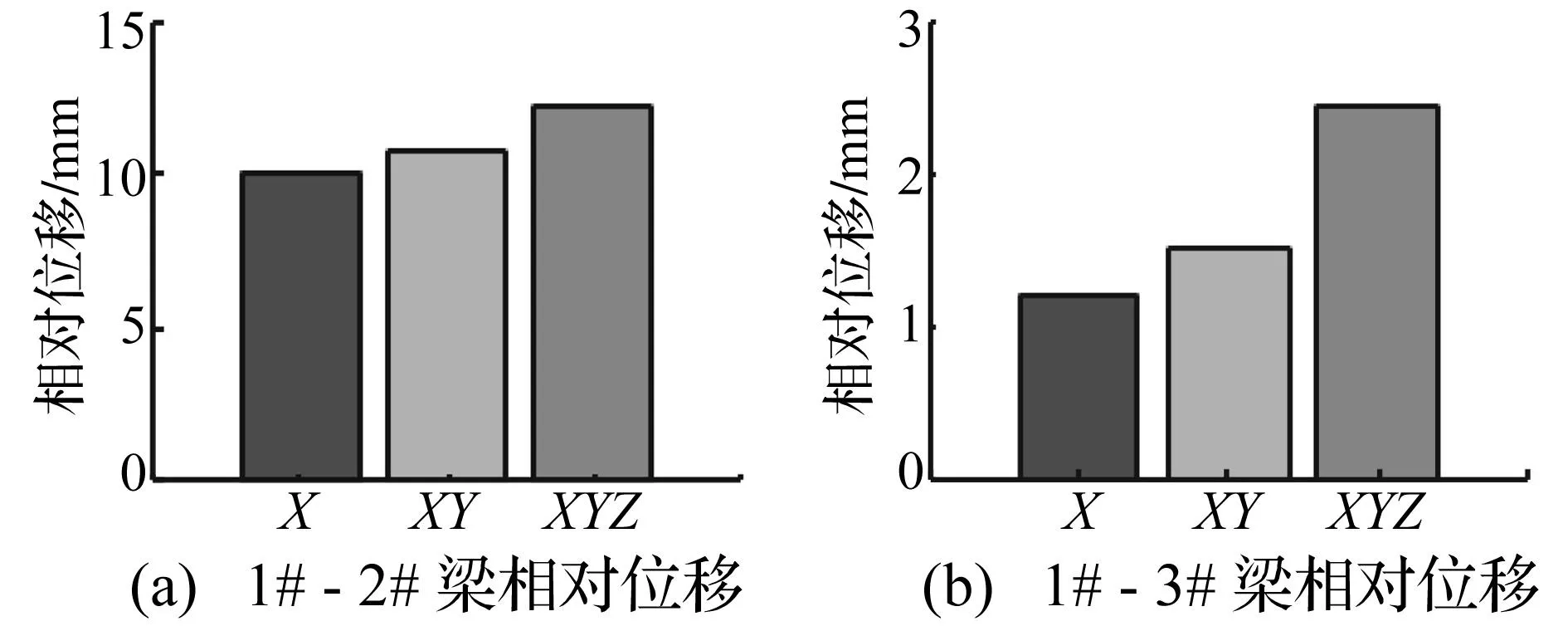
图10　相对位移峰值Fig.10 Relative displacement peak

由图10可知，X向、XY向、XYZ向输入时1#梁与2#梁之间的相对位移依次为10.251 mm、12.971 mm、13.265 mm，1#梁与3#梁之间的相对位移依次为1.306 mm、1.639 mm、2.631 mm。以上结果说明，相比单向输入，双向和三向输入都会使邻梁之间的相对位移增大且主梁与分支直梁的相对位移大于主梁与分支曲梁之间的相对位移；相对位移的大小不仅与地震的输入方向有关，还与相邻梁体的形式和质量分布情况有关。因此，人字形桥梁结构对于分支直梁和分支曲梁处的伸缩缝宽度应根据抗震设防烈度分别进行多维设计，精确计算不同位置处的伸缩缝宽度需求值。

3.4应变响应

历次破坏性巨大地震发生后，比较典型的震害是桥墩底部因受力过大而出现破坏。为此，本文对人字形桥梁每个桥墩底部的应变进行分析研究，各桥墩底部的峰值应变见表6。

由表6可知：

(1) 随着地震烈度的增加各桥墩底部的峰值应变逐渐增强，当地震烈度增加至9度0.4 g时，XY向输入时，各墩底峰值应变最大，相比7度0.1g时，1#墩、2#墩、3#墩、4#墩、5#墩、6#墩底截面最大峰值应变增加率依次为459.2%、919.5%、575.0%、1 105.4%、1 113.5%、1 277.4%。

(2) 比较相同地震烈度时地震波沿不同方向输入时桥墩底部的峰值应变，地震波沿XY向输入时，墩底应变峰值大于沿X向输入，沿XYZ三向输入时相比XY向基本无变化，甚至有一定程度的减小。分析出现这种原因是因为， 双向输入时桥墩应变为两个方向响应

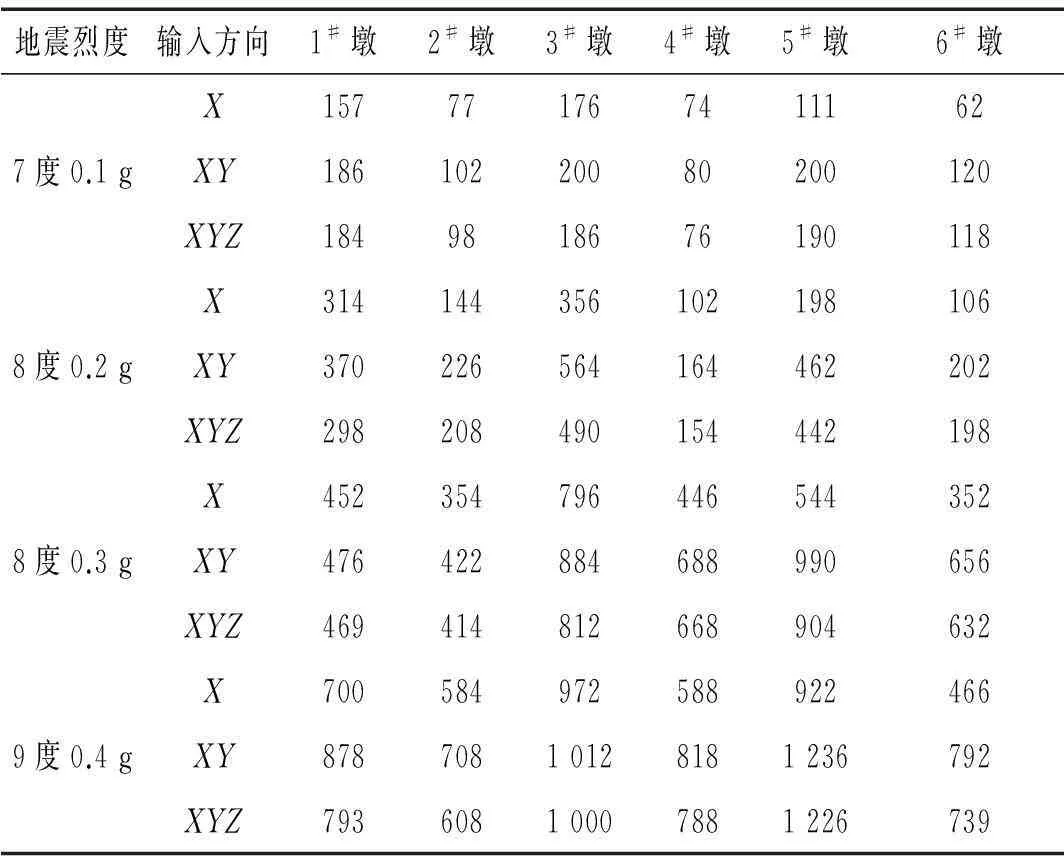
表6　墩底应变峰值(με)

的合成，其结果显然大于单向输入；三向输入时，竖向地震动对桥墩弯曲基本无影响，有时甚至会因梁体压缩桥墩而减小桥墩钢筋的应变。

(3) 主梁下部1#桥墩墩底峰值应变较2#桥墩大，分支直梁3#桥墩墩底峰值应变较2#桥墩大，分支曲梁5#桥墩峰值应变较4#墩、6#墩底峰值应变大。出现上述结果是因为1#、3#、5#桥墩与梁体之间均设有固定支座，地震作用下上部梁体的惯性力通过固定支座传递至下部桥墩，因而这三个桥墩墩底的峰值应变相对较大。

3.5碰撞响应

以图4所示的碰撞装置投入试验，用以测量桥梁在地震作用下邻梁之间的碰撞效应。通过数据分析可知在地震烈度较小时伸缩缝处碰撞不明显，因此本文仅研究在地震烈度为8度0.3 g和9度0.4 g时模型结构钢柱上的碰撞响应(见图11)。

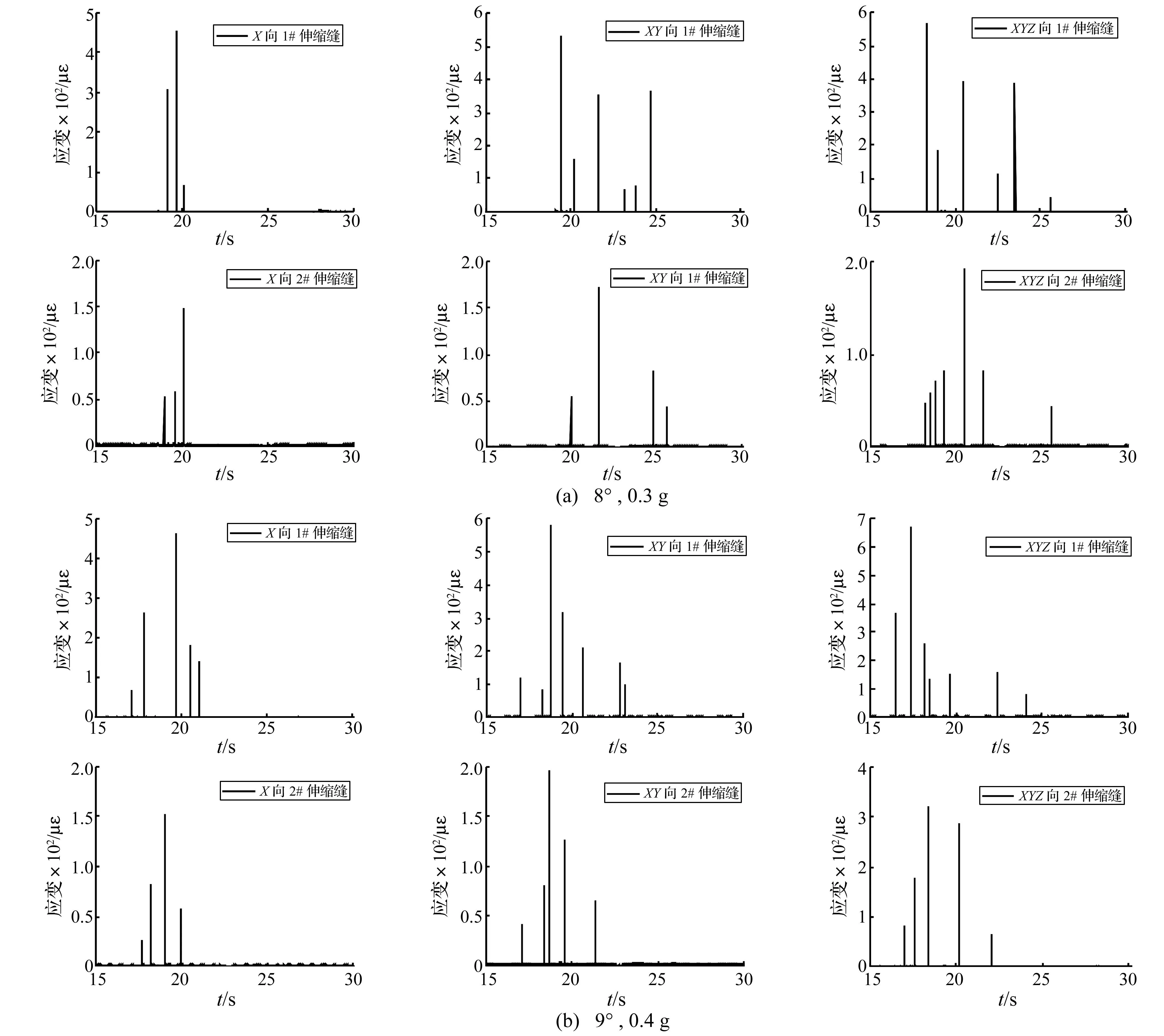
图11　碰撞应变时程Fig.11 Strain history of pounding

表7中分别对图11中对初次碰撞时间、碰撞次数和最大碰撞应变进行了研究。由表7可知，随着地震烈度的增加，主梁与分支梁之间的碰撞响应逐渐增强。从初次碰撞时间和碰撞次数的多少可以发现，输入地震烈度越大、维数越多，主梁与分支梁的初始碰撞时间越早，碰撞次数也越多。相同地震烈度输入，伸缩缝之间的碰撞应变在XYZ三向地震输入时最大，XY双向次之，X单向最小。地震烈度为8度0.3 g时，1#伸缩缝碰撞应变最大值在XYZ向输入时相比XY向和X向输入分别增大6.8%、25.1%；2#伸缩缝XYZ向输入时其碰撞应变最大值相比XY向和X向分别增大11.6%、29.7%。地震烈度为9度0.4 g时，1#伸缩缝碰撞应变最大值在XYZ向输入时相比XY向和X向输入分别增大15.5%、44.7%；2#伸缩缝XYZ向输入时其碰撞应变最大值相比XY向和X向分别增大62.8%、109.9%。地震烈度为8度0.3 g时，分支直梁与主梁的碰撞应变为分支曲梁与主梁的2.96倍；地震烈度为9度0.4 g时，分支直梁与主梁的碰撞应变为分支曲梁与分支直梁的2.10倍。以上分析说明，人字形桥梁伸缩缝处的碰撞响应受地震烈度及地震输入方向的影响较大。在研究人字形桥梁伸缩缝处的碰撞效应时应对其进行设防烈度的多维输入，满足其最不利状态的抗震需求；不同伸缩缝处的不同碰撞应变说明，人字形桥梁应对主梁与分支直梁和分支曲梁处的伸缩缝宽度按不同的设计宽度进行设计。

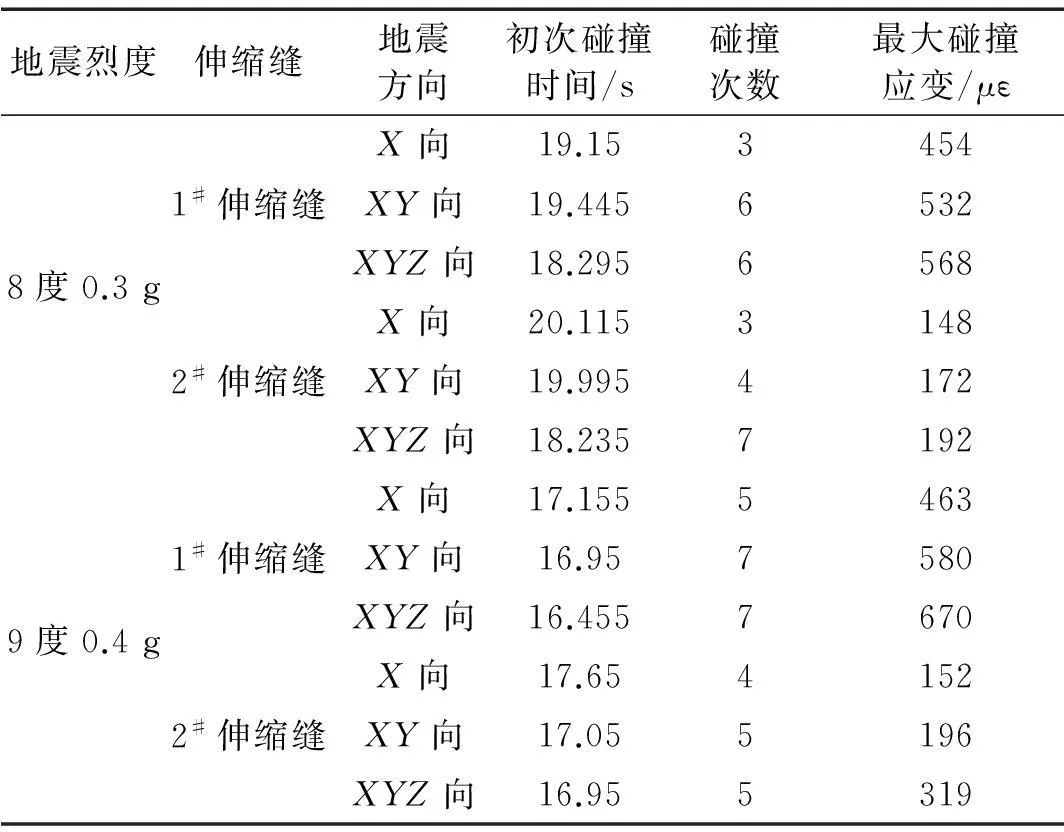
表7　碰撞响应(με)

4有限元分析

4.1分析模型

本文以试验桥梁为对象，采用通用有限元软件Ansys建立模型桥梁的有限元模型，探讨模型桥梁多维激励下有限元计算结果与试验与结果的吻合程度。

4.1.1支座单元模拟

模型桥梁中存在固定支座与滑动支座两种类型支座。固定支座表现为刚塑性，其初始刚度非常大，超过设计水平力则支座破坏，刚度为零；计算模型中，支座刚度取试验中实测数据。有限元模型中1#、3#、5#墩与梁之间固定支座采用3个combin14单元模拟，2#、4#、6#墩与梁之间的滑动支座水平刚度采用两个combin40单元模拟，竖向刚度采用1个combin14单元模拟。

4.1.2伸缩缝单元模拟

为模拟伸缩缝处的碰撞，伸缩缝处采用图12所示的碰撞单元模拟，有限元软件中碰撞单元采用combin40单元模拟。接触单元的非线性力-位移关系如式(1)所示。

图12　伸缩缝模拟Fig.12 Movement joint model

(1)

式中:d0为伸缩缝初始间隙;x为地震作用下伸缩缝处相邻梁体的相对位移;k为接触刚度。根据以往研究，碰撞刚度取为梁体的轴向刚度[20]，本文碰撞刚度k=5.376×107N/m。碰撞过程中的能量损失采用阻尼比表示,阻尼的大小与碰撞过程的恢复系数e有关，对于混凝土材料e取0.65[21]。根据恢复系数,可得到阻尼的计算公式为:

(2)

(3)

式中：m1和m2分别为伸缩缝相邻联梁体的质量。

4.1.3主梁、桥墩及边界条件模拟

为减小误差1#异形梁建模时采用空间梁格法建立，梁格分割箱梁的同时保证荷载正确传递，分割后的后的构件单元和刚性梁单元分别BEAM188 和MPC184 单元建立，2#和3#梁采用BEAM188单元。桥墩均采用beam4单元模拟。有限元模型边界条件为墩底全固结，在计算地震荷载时，去掉桥墩底部地震波输入方向上的约束并在此方向上输入地震加速度。

根据以上建模原则，模型桥梁有限元模型见图13。

图13　有限元模型Fig.13 Finite element model

4.2主要计算结果

4.2.1结构动力特性比较

由于有限元软件中较难模拟结构在损伤状态下的一阶频率，故本文仅将有限元软件计算的结构无损伤状态的一阶频率与试验前的白噪声扫描结果进行对比见表8。分析表8数据可知，X方向一阶频率误差均在6.1%以内，Y方向的一阶频率误差为6.4%以内，Z方向的一阶频率误差均在9.2%以内，计算结果与试验结果基本一致。分析引起误差的原因主要是由于模型制作误差，模型配重不均匀以及测试仪器精度等。

4.2.2加速度响应比较

表9为8度0.2 g时墩顶顺桥向各测点加速度有限元计算与试验结果的对比情况，其中最大误差为9.5%。引起此差别的主要原因除了动力特性对比中

所列出的原因之外还有因为限元建模中加速度可以足值输入，但实际模型在地震波加载过程中并非完全按理论加速度峰值等值输入。

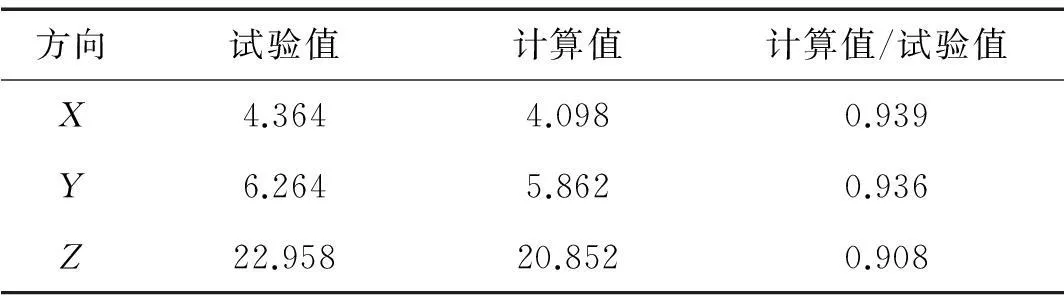
表8　频率计算值与试验值比较(Hz)

4.2.3邻梁相对位移比较研究

表10给出了8度0.3 g时试验与有限元计算结果对比数据，其中1#～2#梁间相对位移峰值最大误差为13.0%。引起此差别的主要原因除以上原因外，还因为伸缩缝处碰撞单元参数的选取是根据理论计算结果输入，其与实际模型桥伸缩缝处设置的碰撞装置存在一定差异。

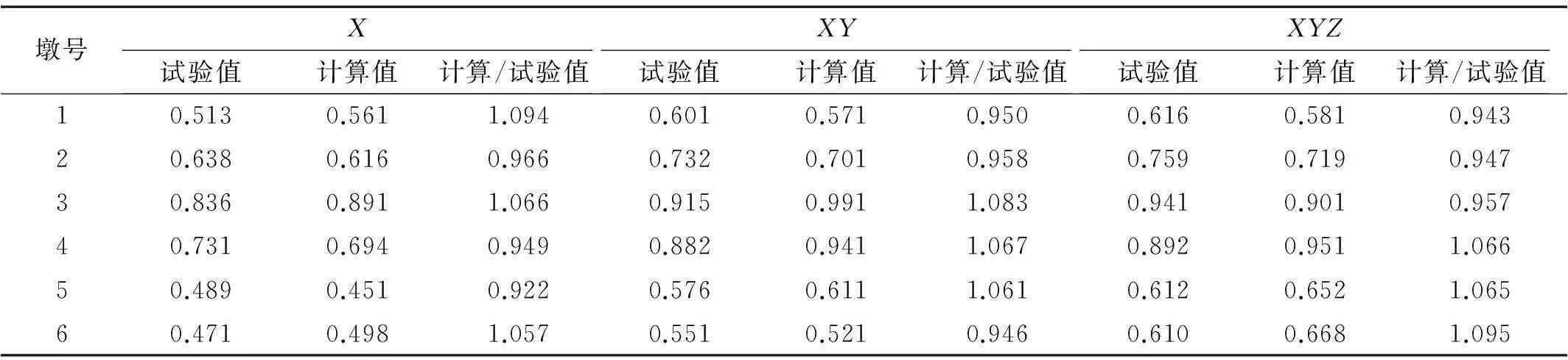
表9　加速度计算值与试验值比较(g)

表10　相对位移计算值与试验值比较(mm)

5结论

本文通过对一座缩尺比例的人字形桥梁进行多维激励的地震模拟振动台试验与有限元分析得到以下结论：

(1) 桥墩顶顺桥向加速度响应大小与地震输入烈度成正比。桥墩顶顺桥向加速度响应基本不受竖向地震分量的影响。双向和三向激励均使分支曲梁下部桥墩顶顺桥向加速度响应相对于单向激励降低，且降低幅度随着墩与地震波X向输入角度的增加而增加。因此对人字形桥梁结构墩顶加速度响应进行计算分析时，不需考虑多维输入，仅沿分支直梁方向输入即为其最不利地震输入方向。

(2) 梁跨中竖向加速度响应说明水平地震响应可引起桥梁结构的竖向振动，且分支曲梁对水平向地震动的敏感程度较分支直梁明显。竖向地震动输入对分支直梁的竖向振动响应较分支曲梁显著。故对人字型桥梁梁体竖向加速度响应进行计算时应考虑水平向加速分量的影响。

(3) 邻梁之间的相对位移与地震波的输入方向密切相关，多维输入使得分支直梁和分支曲梁处的伸缩缝宽度需求增加，因此在计算伸缩缝宽度时应根据抗震设防烈度进行多维设计。

(4) 双向输入使得桥墩底部的应变需求增大较明显，三向输入对桥墩底部应变基本无影响，甚至会减小墩底应变，因此在计算桥墩墩底应变响应时仅对其进行双向输入即可。

(5) 双向和三向输入使得邻梁之间的初始碰撞时间提前，碰撞次数增多，碰撞应变增大，且三向输入较双向输入更不利。在实际设计中，考虑碰撞效应时应对结构进行三向输入。

参 考 文 献

[ 1 ] 周颖，吕西林. 建筑结构振动台模型试验方法与技术[M]. 北京：科学出版社，2012.

[ 2 ] 闫晓宇,李忠献,韩强,等. 考虑土-结构相互作用的大跨度连续刚构桥振动台阵试验研究[J]. 工程力学,2014,31(2):58-65.

YAN Xiao-yu, LI Zhong-xian, HAN Qiang, et al. Shaking table test on a long-span rigid-frawed bridge considering soli-structure interaction[J]. Engineering Mechanics,2014,31(2):58-65.

[ 3 ] 韩强，杜修力，刘晶波,等. 多维地震作用下隔震桥梁地震反应(Ⅰ)-模型结构振动台试验[J]. 振动与冲击，2008,27(9):59-68.

HAN Qiang, DU Xiu-li, LIU Jing-bo, et al. Swismic response of isolated bridges with LRB under muldi-directional earthquake Part(Ⅰ)-Shaking table test of bridge model[J]. Journal of Vibration and Shock, 2008, 27(9): 59-68.

[ 4 ] 钟栋青,王曙光,刘伟庆. 连续梁桥纵向减震性能振动台试验与理论分析[J]. 土木工程学报,2012,(45)11:147-152.

ZHONG Dong-qing, WANG Shu-guang, LIU Wei-qing, Shaking table experimental study and theoretical analysis of the longitudinal seismic-reduced behavior of continuous-beam bridges[J]. China Civil Engineering Journal, 2012,(45)11: 147-152.

[ 5 ] 黄福云,李建中,陈宝春,等. 钢管混凝土单圆管拱结构振动台阵试验研究[J]. 工程力学,2014,31(4):82-92.

HUANG Fu-yun, LI Jian-zhong, CHEN Bao-chun, et al. Shaking table test of concrete filleed stell tubular arc rib model[J]. Engineering Mechanics, 2014,31(4):82-92.

[ 6 ] Saiidi M S, Vosooghi A, Choi H, et al. Shake table studies and analysis of a two-span RC bridge model subjected to a fault rupture[J]. Journal of Bridge Engineering, 2014,19(8):1-9.

[ 7 ] Saiidi M S, Vosooghi A, Nelson R B. Shake-table studies of a four-span reinforced concrete bridge[J].Journal of Structural Engineering, 2012, 139(8): 1352-1361.

[ 8 ] Williams D, Godden W. Seismie response of long curved bridge structures: experimental model studies[J]. Earthquake Engineering and Structural Dynamics,1979(7):107-128.

[ 9 ] Wieser J, Zaghi A E, Maragakis M, et al. A methodology for the experimental evaluation of seismic pounding at seat-type abutments of horizontally curved bridges[J]. Bridges, 2014, 10: 9780784412367.055.

[10] 黄海云,张俊平. 人字形桥梁受力行为的参数分析[J].广州大学学报:自然科学版, 2003,2(5): 472-476.

HUANG Hai-yun, ZHANG Jun-ping. Parameter analysis for working behavior of Y-shape bridge[J]. Journal of GuangZhou University:Natural Science Edition, 2003, 2(5): 472-476.

[11] 卢彭真，张俊平，赵人达.典型人字形桥梁模型试验研究与分析[J].工程力学,2008,25(3):139-143.

LU Peng-zhen,ZHANG Jun-ping, ZHAO Ren-da.Analysand study on model experiment of typical Y-shaped bridge[J].Engineering Mechanics,2008,25(3):139-143.

[12] 张敏政.地震模拟实验中相似律应用的若干问题[J]. 地震工程与工程振动, 1997, 17(2): 52-58.

ZHANG Min-zheng.Study on similitude laws for shaking table tests[J]. Earthquake Engineering and Engineering Vibration, 1997,17(2):52-58.

[13] 沈德建,吕西林. 模型试验的微粒混凝土力学性能试验研究[J]. 土木工程学报,2010,43(10):14-21.

SHEN De-jian, LÜ Xi-lin. Experinmental study on the mechanical property of microconcrete in model test[J]. China Civil Engineering Journal, 2010,43(10):14-21.

[14] Mir R A,Taylor C A.An experimentalinvestigation into earthquake induced failure of mediumto low height concrete gravity dam[J].Earthquake Engineering Structural Dynamics,1995,24:378-393.

[15] 林皋，朱彤，林蓓.结构动力模型试验的相似技巧[J].大连理工大学学报，2000,41(1):1-8.

LIN Gao, ZHU Tong, LIN Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000,41(1):1-8.

[16] JTG/T B02-01-2008. 公路桥梁抗震设计细则[S]. 北京：人民交通出版社，2008.

[17] GB50011-2010. 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2010.

[18] Kunnath S K, Erduran E, Chai Y H, et al. Effect of near-fault vertical ground motions on seismic response of highway overcrossings[J]. Journal of Bridge Engineering, 2008, 13(3): 282-290.

[19] Papazoglou A J, Elnashai A S. Analytical and field evidence of the damaging effect of vertical earthquake ground motion[J]. Earthquake Engineering and Structural Dynamics, 1996, 25(10): 1109-1138.

[20] Malhotra P K. Dynamics of seismic pounding at expan-sion joints of concrete bridges[J]. Journal of Engineering Mechanics, ASCE, 1998, 124(7): 59-72.

[21] Jankowski R, Wilde K, Fujino Y. Reduc-tion of pounding effects in elevated bridges during earthquakes[J]. Earthquake Engineering and Structural Dynamics, 2000,29: 195-212.

Shaking table tests for Y-shaped bridges under multi-dimensional seismic excitation

YANLei,LIQing-ning,YINJun-hong,HANChun,CHENGMai-li(Civil Engineering School, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Abstract:In order to study sesimis responses of Y-shape bridges under earthquake, based on a existing Y-shape bridge, a scale 1/20 model of Y-shaped curved bridge was constructed, El-centro waves were used to make a shaking table test with different earthquake intensity and multi-dimensional seismic excitation. Besides, the finite element analysis were also conducted for this model bridge. The research results showed that when the earthquake intensity is enhanced, the fundamental frequency of the model bridge decreases and its damping ratio increases; the longitudinal acceleration response of pier’s top is not affected by the vertical earthquake excitation; the horizontal bidirection earthquake excitation can meet the requirement when calculating the strain response at bottom of a pier; the vertical acceleration response of the mid span, expansion joints width between the main beam and branch beams and pounding response at expansion joint are related to seismic wave input dimension; therefore, when designing Y-shaped bridges, multi-dimensional seismic excition should by chosen according to different design purposes.

Key words:Y-shaped bridge; multi-dimensional excition; shaking table test; finite element analysis; seismic design

中图分类号:U442.55

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.026

通信作者李青宁 男，教授，博士生导师，1952年生

收稿日期：2015-07-06修改稿收到日期：2015-09-23

基金项目：国家自然科学基金(51078306)；国家自然科学基金青年基金(51408453)；陕西省自然科学基础研究计划资助项目(2013JQ7007)

第一作者 闫磊 男，博士生，1988年生