基于行星滚柱丝杠副的机电作动器动态特性分析

乔　冠， 刘　更， 马尚君， 佟瑞庭， 周　勇

(西北工业大学 陕西省机电传动与控制工程实验室，西安　710072)



基于行星滚柱丝杠副的机电作动器动态特性分析

乔冠， 刘更， 马尚君， 佟瑞庭， 周勇

(西北工业大学 陕西省机电传动与控制工程实验室，西安710072)

摘要：以舵回路系统中机电作动器为研究对象，考虑机电作动器的安装和舵面负载连接，建立了基于行星滚柱丝杠副的机电作动器数学模型。采用AMESim进行仿真对比分析，探讨了机电作动器中结构刚度、摩擦和间隙等非线性因素对系统动态性能的影响。结果表明：相比传动刚度，结构刚度中固定刚度的提高对于系统动态响应的改善作用更明显；行星滚柱丝杠副间隙量越大，系统的阶跃响应波动幅值越明显；在给定舵控指令下，机电作动器的仿真位移输出响应误差最大为1.8 mm，相对误差为1.2%，从而较好的反映了模型的有效性，为功率电传机电作动器的进一步结构优化和控制提供理论依据。

关键词：机电作动器；行星滚柱丝杠副；动态特性；结构刚度；间隙非线性

机电作动器(Electro-Mechanical Actuator，EMA)是功率电传作动系统的一个分支，由于其具有重量轻、工作效率高、系统可靠性高和便于维护[1-2]等优点，广泛应用于飞行舵面控制、推力矢量控制、飞机刹车和工业过程控制等军民领域。

国外在EMA动态特性研究方面起步较早，建立了EMA系统级功率键合图模型和基于AMESim环境的EMA仿真模型，对采用反向式行星滚柱丝杠副的EMA进行动态性能测试，通过力矩和转速干扰实验验证模型的有效性[3]。Karam等[4]讨论了力控制的基于行星滚柱丝杠副的EMA中摩擦、转子惯量和测试平台刚度等因素的影响，这些因素都会改变EMA的稳态和动态特性。Mare等[5-6]提出基于仿真模型的EMA功率传递初步设计准则，以确保测试平台结构与目标动态性能的一致，考虑了结构部件的静态与动态性能的限制，从而使得控制器设计更简单。Habibi等[7]分析了控制飞机舵面的EMA动态特性，表明由空程和静态摩擦产生的死区是限制EMA输入输出特性的重要因素，并通过使用内环控制策略减小死区对系统的影响。国内20世纪90年代初才开始研究包括机电作动器和电动静液作动器(Electro-Hydrostatic Actuator，EHA)在内的功率电传作动器，已证实该技术的可行性和有效性。齐海涛等[8]基于AMESim对EHA进行了建模和仿真分析，仿真结果表明所设计的EHA动态性能良好，达到了预定的性能指标。马尚君等[9]建立了EMA中的标准式行星滚柱丝杠副有限元模型，基于显式动力学有限元算法对其动态特性进行仿真分析，为研究EMA整体性能的提高提供参考。国内学者多数的研究工作集中于EMA的复合式余度控制[10]、混合作动系统研究[11]等方面，然而对基于行星滚柱丝杠副的EMA中结构刚度、摩擦和间隙因素对EMA动态特性影响研究较少涉及，鲜有文献报道考虑EMA的安装和舵面负载连接并建立数学模型。

本文考虑EMA的安装、EMA与舵面负载的连接，建立了基于行星滚柱丝杠副的EMA数学模型。采用AMESim仿真分析，分别探讨了舵回路系统中EMA的结构刚度、摩擦和间隙等非线性因素对系统的动态性能影响。在相同给定的舵控指令下，对比本文EMA与传统伺服油缸的位移跟踪精度，结果表明建立的EMA模型是有效的。

1EMA系统组成

1.1EMA结构形式

典型的EMA在飞行器舵回路系统中的组成见图1，EMA主要由无刷直流电机、控制器(主要包括速度、位置控制器和功率变换器)、齿轮减速器(或者带传动)、滚珠丝杠副(或者行星滚柱丝杠副)这四部分组成。其中，滚珠丝杠副(Ball Screw Mechanism, BSM)和行星滚柱丝杠副(Planetary Roller Screw Mechanism, PRSM)作为EMA中的执行机构，用来传递扭矩、进行运动变换。PRSM用滚柱作为中间传动体，用滚动摩擦取代滑动摩擦，具有效率高、寿命长、承载能力强等特点。其中，标准式行星滚柱丝杠副(Standard Planetary Roller Screw Mechanism, SPRSM)主要传动装置有丝杠、螺母和滚柱，其基本结构见图2。本文以基于SPRSM的EMA为对象建模并进行其动态特性研究分析。

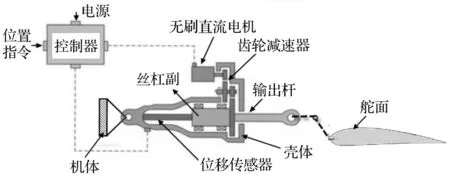
图1　舵回路系统中的EMA结构Fig.1 The basic structure of EMA in actuator loop

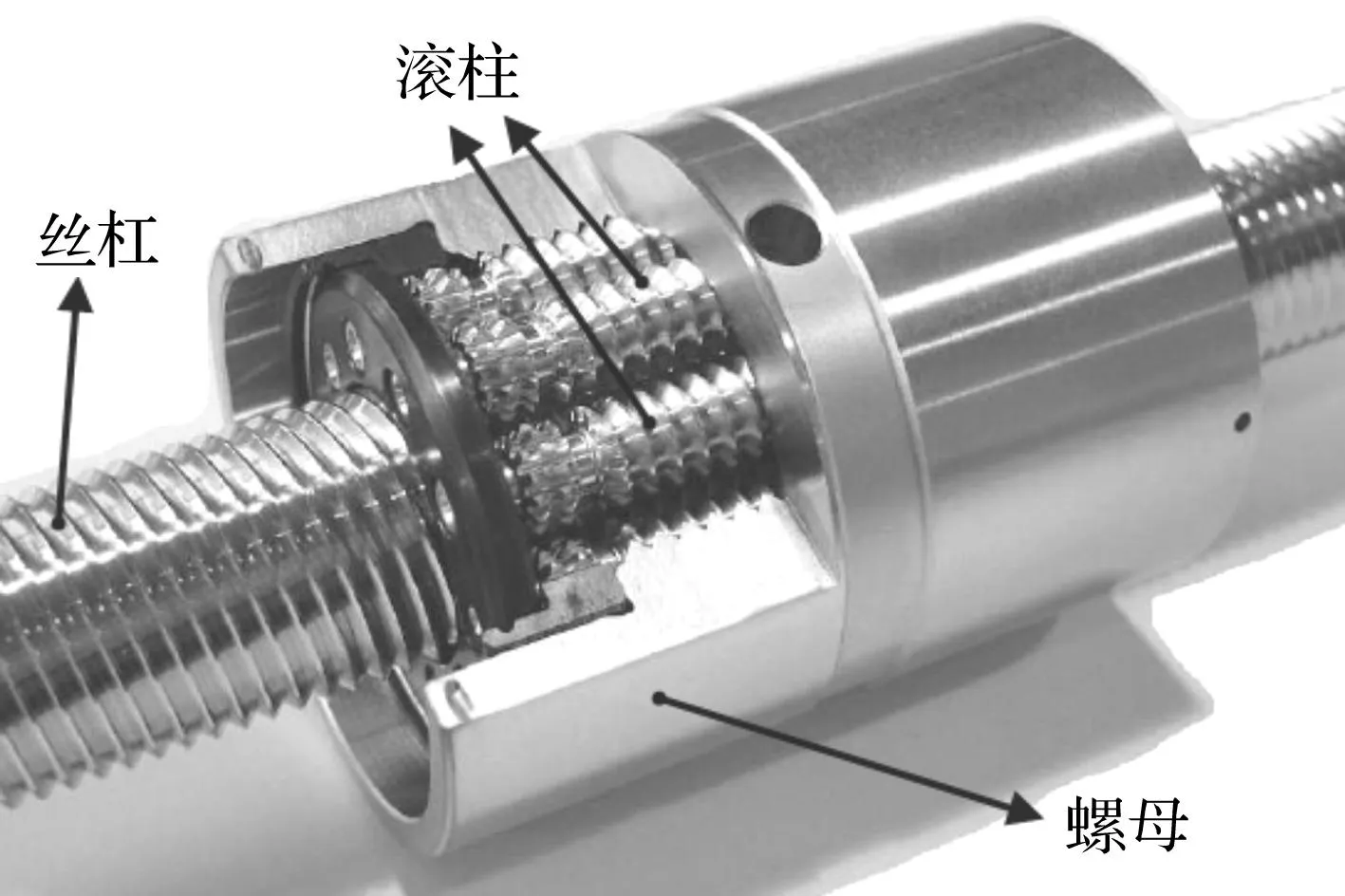
图2　SPRSM基本结构Fig.2 The basic structure of SPRSM

1.2EMA在舵回路系统中的工作原理

EMA通过铰链安装于机体，并由其输出杆带动摇臂等连接机构，最终实现舵面的位置控制(见图1)。控制器接受来自飞控计算机的舵控指令，驱动无刷直流电机做正反向运动，再通过齿轮装置减速增扭，把丝杠的旋转运动转化为输出杆相对于壳体的直线运动，驱动舵面实现相应的动作。同时，电机中的电流信号，电机输出轴的转速信号和舵面的位置信号都通过反馈参与到控制器的运算实现闭环反馈控制。

2EMA系统建模

结合图1，在AMESim中建立的EMA整个系统模型见图3，部分子模型采用超级元件封装。EMA的建模主要包括：“a”为正弦或给定的信号指令输入；“b”和“c”分别为电机控制器和无刷直流电机数学模型；“d”和“e”分别为齿轮副和SPRSM的机械传动模型；“f”和“g”为考虑作动器固定机构和连接机构的等效刚度和阻尼；“h”为舵面及气动力负载模型。

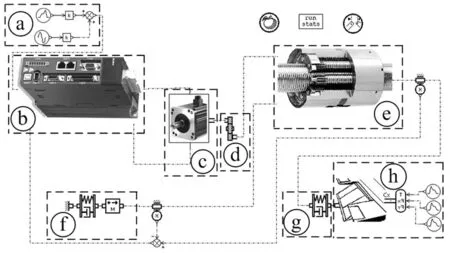
图3　EMA系统模型Fig.3 EMA model in AMESim environment

2.1控制器模型

控制器是EMA的重要组成部分，为防止电枢电流过载，保证电机的响应速度和动态特性，控制器采用电流、速度双闭环，两环均采用PI控制；位置环采取简单的比例控制(见图4)。该模型还包括信号采样、电压电流限幅以及力闭环反馈等。

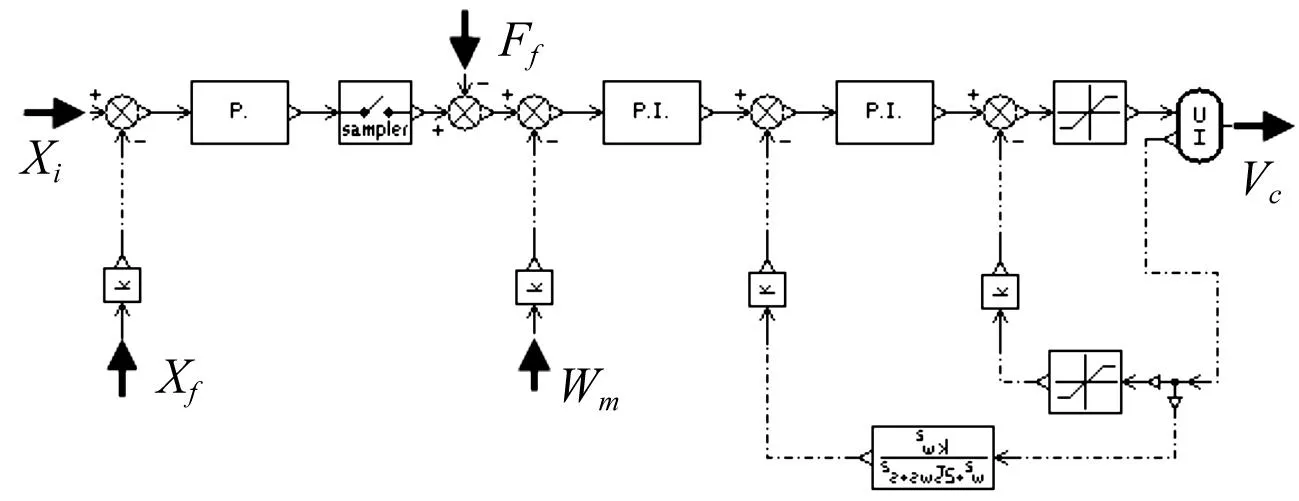
图4　控制器模型Fig.4 The controller model

2.2电机模型

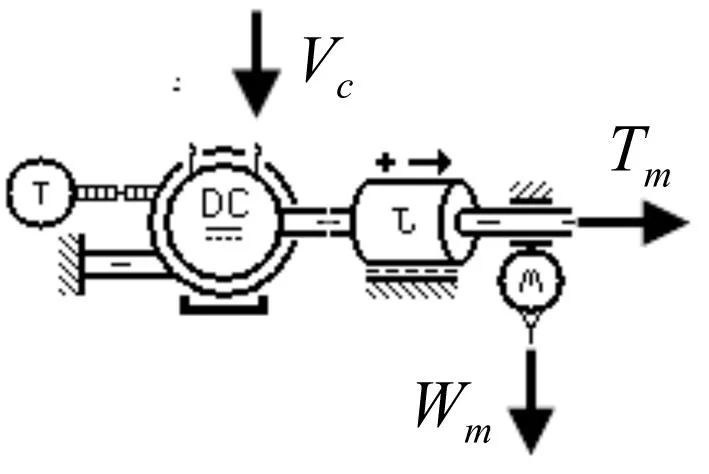
图5　电机模型Fig.5 The motor model

采用270 V永磁无刷直流电机，选用AMESim电机及驱动库中的直流电机模型(见图5)。参照表1，电机的电枢电流Ic与输入电压Vc的关系通过一个一阶传递函数Ge描述

Ic=Ge(Vc-Kωωm)

(1)

(2)

式中：ωm为电机输出角速度;Kω为反电动势系数;Rc为电机绕组电阻;Lc为电机绕组电感;τe为电机的电气时间常数。电机产生的力矩表达式为

Tm=KcIc

(3)

当电流饱和时服从表达式

Tpeak=KcIlim

(4)

式中：Kc为电机电磁力矩常数;Tm为电机输出力矩;Tpeak为电机最大输出力矩;Ilim为电机的电枢饱和电流。考虑到电机和丝杠副通过齿轮减速器相连，施加在电机轴上的力矩表达式为

(5)

式中：Jm为折算到电机轴的转动惯量;Kmv为电机摩擦系数;Tload为负载力矩;i为机械系统的传动比，即齿轮副减速比与丝杠副减速比之积。

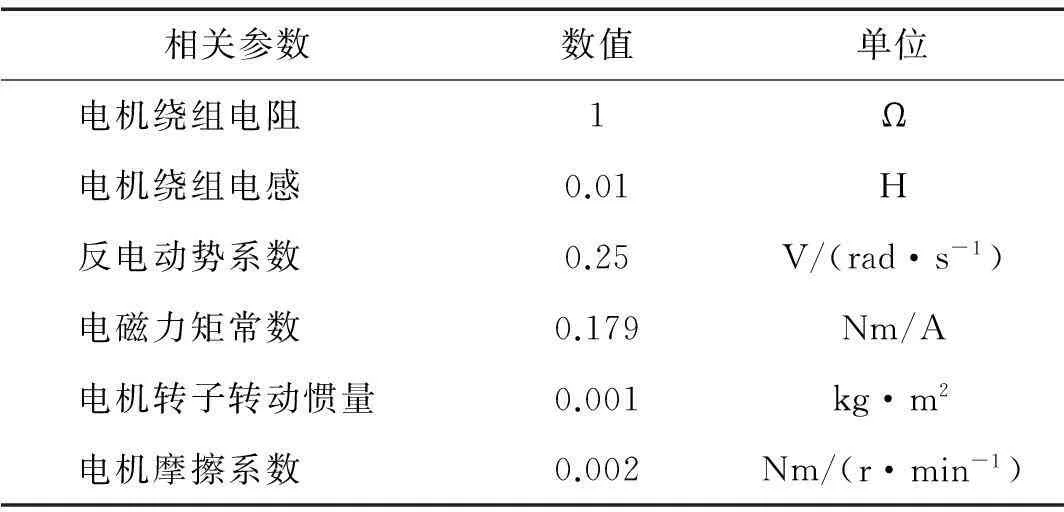
表1　电机的相关参数设置

2.3SPRSM模型

SPRSM模型考虑了部件的移动和转动部分，并综合计入了摩擦和间隙非线性因素。EMA中的摩擦非线性影响是降低系统控制性能因素之一。由于单独分离EMA中SPRSM、角接触球轴承和输出杆等处的摩擦力非常困难，一般将这些摩擦力等效为输出杆端的整体摩擦力。这样可将EMA建成带有集中摩擦耗散的理想功率转化模型。在恒速时，电机的输出力矩Tm为摩擦力矩Tfric和负载端输出力矩Tload之和。

(6)

(7)

式(6)和式(7)中的l为SPRSM的导程，Fext为负载端承受的外力，Ffric为输出杆端的整体摩擦力。EMA的整体摩擦力是外力和电机转速的函数。为了简化复杂的因果关系，可通过式(8)对整体摩擦力进行建模，该模型考虑了负载端承受的外力。

(8)

式中：Fc为Coulomb摩擦力;Fs为Stribeck摩擦力;ωs为参考速度;c为外力影响平均系数;d为象限决定系数。摩擦力矩Tfric的公式为

(9)

式中：Tc和Ts分别为Coulomb摩擦力和Stribeck摩擦力产生的力矩。在AMESim的机械库中选择旋转摩擦块，用力传感器和转速传感器作为输入变量计算负载摩擦力矩，建立的三端口模型(见图6)。

图6　SPRSM的三端口模型Fig.6 Three mechanical ports model of SPRSM

2.4舵面模型

AMESim是面向对象的液压/机械系统建模、仿真及动力学分析软件。本文在建立舵面模型时，选用其平面机构库中的模型模拟舵面的实际情况。包括舵面安装铰链、舵面质心、加载位置及摇臂的建模等，提供了更丰富的力与力矩加载(见图7)。这样不仅可以仿真舵面的负载特性，还可以通过三维可视化功能AMESim-Animation观察舵面的实际运动情况。

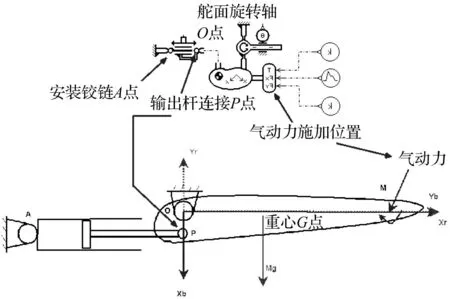
图7　舵面模型Fig.7 The rudder model

3EMA动态特性分析

设置控制指令为0.1 s时刻的0.1 V阶跃信号，经转化比例系数，即为1 mm阶跃信号，系统仿真时间为10 s，在5 s时加入10 000 N的阶跃冲击力，参数见表1和表2。

表2　EMA系统的相关参数设置

3.1传动间隙非线性因素影响

间隙是限制速度与位置控制性能高低的最重要非线性影响因素之一。EMA的间隙主要包括PRSM中丝杠侧与螺母侧的轴向间隙，齿轮传动中的齿侧隙和轴承轴向间隙等。间隙的存在使得EMA在反向作动时产生作动器位置输出误差，影响作动器位置输出精度。由于传动链中尺寸误差、安装误差和长期磨损，间隙不能完全消除。间隙非线性可以采用Physical模型、Phase plane模型、Dead zone模型和Rubber模型来表示。Dead zone模型是Physical模型的简化，在转轴无阻尼或小阻尼时Dead zone模型是一种有效的模型[12]。此模型中，轴的力矩正比于轴的扭转角

Tm=ksθs=ksDα(θd)

(10)

θs=θd-θb

(11)

死区函数Dα定义为

(12)

此时轴的模型假设为纯弹簧，不计惯量和内部阻尼，并且在不接触时处于稳定状态(见图8)。如果考虑轴的内部阻尼，修正的Dead zone模型如式(13)。

图8　Dead zone模型Fig.8 Dead zone model

(13)

在图4所示的EMA系统模型中，设置间隙值分别为0.002 mm、0.02 mm和0.05 mm，其余参数设置如表2，其阶跃响应仿真结果见图9～图11。

图9　间隙值为0.002 mm的系统阶跃响应Fig.9 EMA step response when the clearance is 0.002 mm

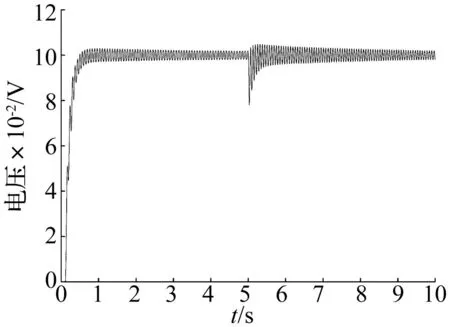
图10　间隙值为0.02 mm的系统阶跃响应Fig.10 EMA step response when the clearance is 0.02 mm

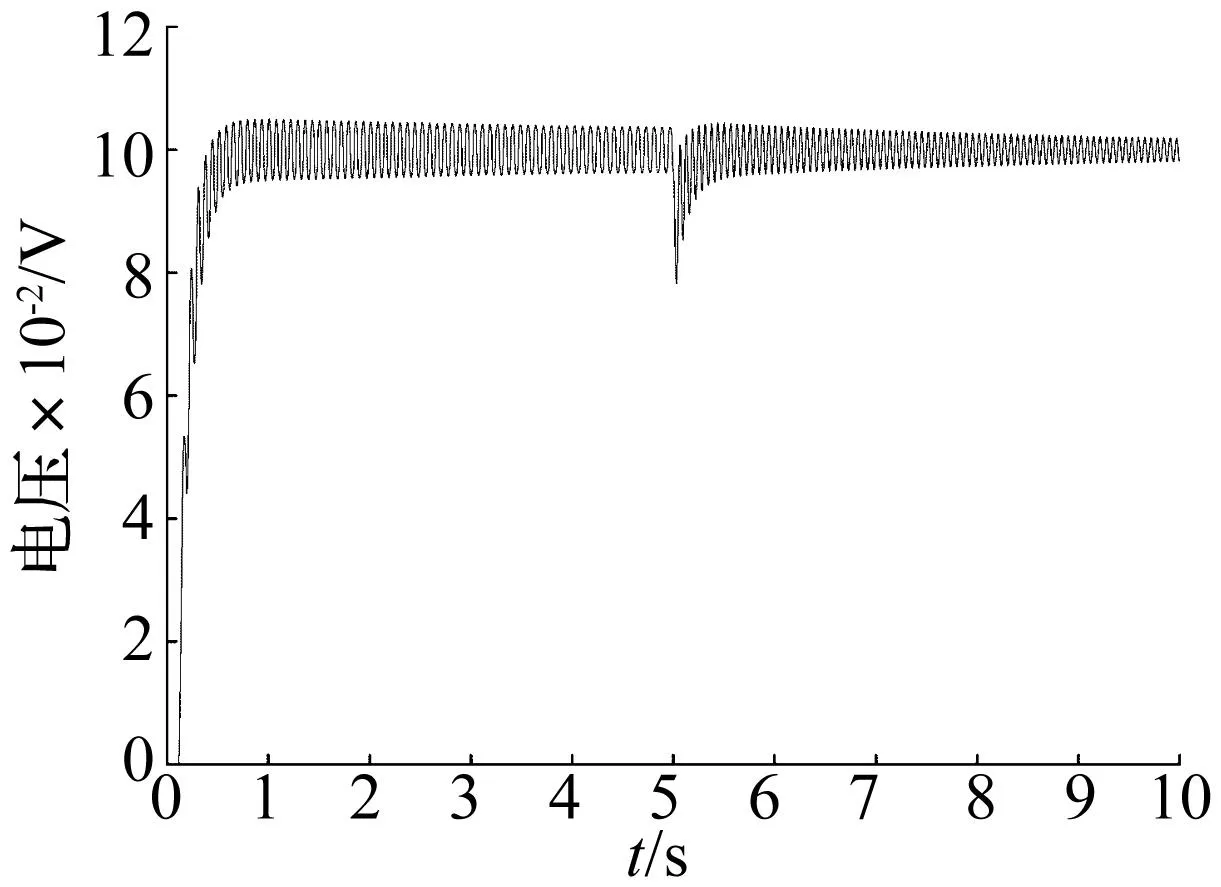
图11　间隙值为0.05 mm的系统阶跃响Fig.11 EMA step response when the clearance is 0.05 mm

对比图9～图11的三条系统响应曲线可知，不同大小的间隙值对系统的影响程度不同，间隙量越大，系统的阶跃响应波动幅值越明显。在EMA中，间隙影响的不仅是控制精度，还对系统的稳定性产生重大影响。为改善EMA的动态输出响应，从机械方面，采用消隙齿轮结构，对PRSM预紧；从材料方面，采用抗磨损材料；从控制方面，通过软件和控制策略进行间隙补偿等。

3.2摩擦非线性因素影响

采用前述图6建立的SPRSM摩擦模型，由式(9)可求得摩擦力矩，图12比较了考虑摩擦和不考虑摩擦模型的系统阶跃响应，此时假设机械传动中不存在间隙。

图12　考虑摩擦和不考虑摩擦模型的响应对比图Fig.12 EMA step response considering friction or not

可见，考虑摩擦的系统存在更大的误差，应通过力闭环反馈改善。在AMESim模型中的等效连接结构与舵面间加入力传感器，将测量到的力信号反馈到控制器形成闭环(见图13)。同时在反向通道内加入一阶低通滤波器，结构为

(14)

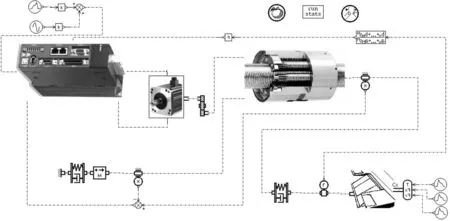
图13　加入力反馈的EMA模型Fig.13 EMA model with force closed-loop feedback

从图14可知，加入力闭环反馈后，响应曲线的振荡幅值小于无力闭环反馈的工况，同时系统的静态误差减小。同样，常用减小机械系统中摩擦的方式可改善运动部件的润滑条件，采用抗摩擦材料以及软件进行摩擦补偿等。

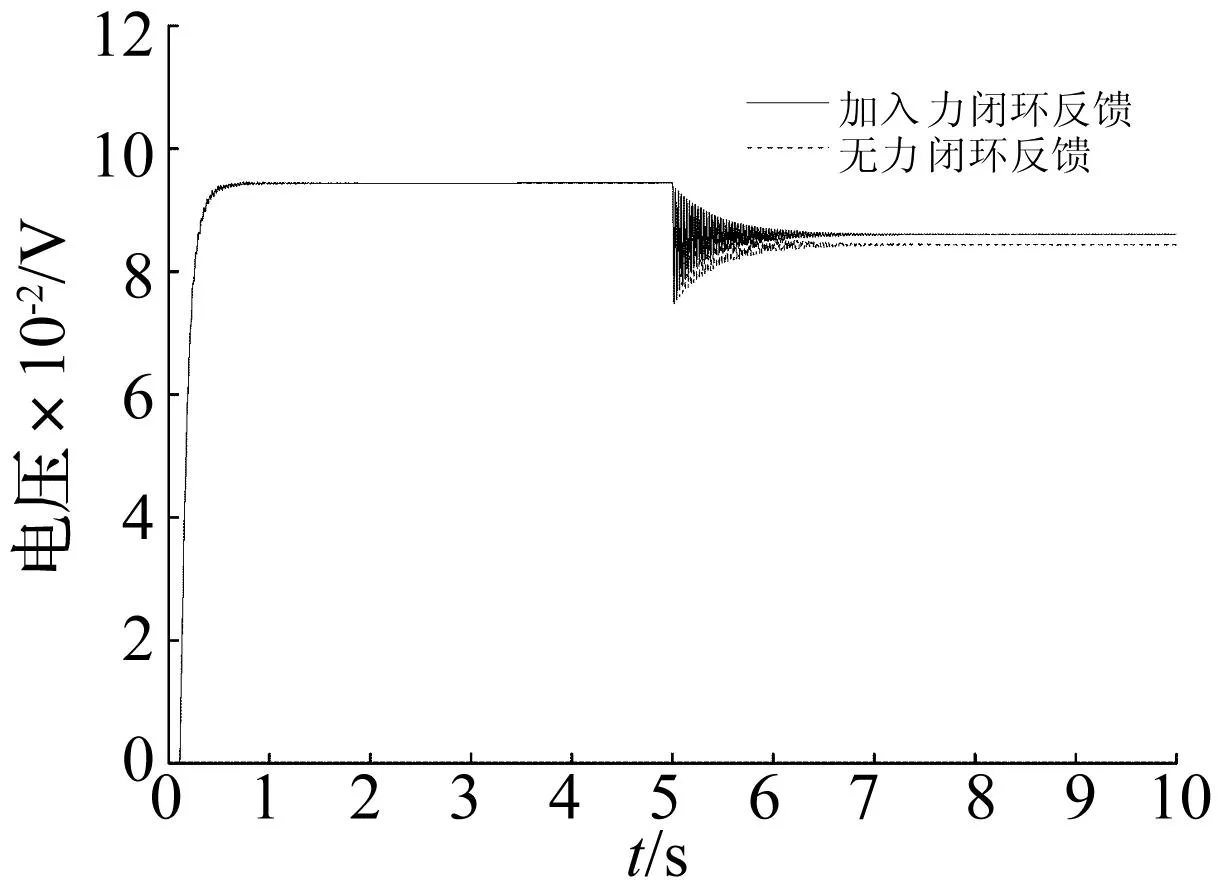
图14　考虑力闭环反馈的系统响应对比图Fig.14 EMA step response with force closed-loop feedback

3.3固定刚度和传动刚度的影响

实际舵回路系统中，机体和被控舵面的刚度并不是无限大。本文在EMA系统建模时采用集中参数法考虑了壳体与机体间和输出杆与舵面负载间的弹簧效应。由于负载系统中含有以柔性结构相连的多级共振性负载，因此EMA壳体和舵面不能简单采用单质量-单弹簧系统近似，而应考虑输出杆与被控舵面间的传动刚度和固定壳体的固定刚度(统称为结构刚度)[13]。KZ1为固定刚度;KZ2为传动刚度。

从图15～图16可知，结构刚度对EMA的动态性能影响较大。当固定刚度和传动刚度均为1×107N/m时，系统的阶跃响应存在小幅值振荡，在5 s时刻施加10 000 N的阶跃冲击力会使系统振荡的幅值更剧烈，不利于系统的快速稳定。从图17可知,此时的谐振频率为7.75 Hz，此振荡频率由2 000 kg的舵面质量，与一条等效弹簧串联得到。

图15　固定刚度和传动刚度均为1×107 N/m时系统阶跃响应Fig.15 EMA step response when anchorage compliance and transmission compliance are 1×107 N/m

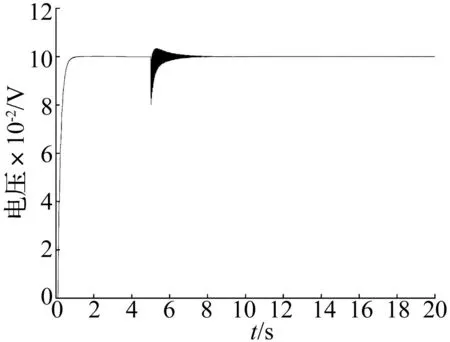
图16　固定刚度和传动刚度均为5×108 N/m时系统阶跃响应Fig.16 EMA step response when anchorage compliance and transmission compliance are 5×108 N/m

弹簧等效刚度值Keq为

(15)

式中：KZ3为螺母和输出杆间的连接刚度;具体数值见表2。经计算可知，图17中峰值频率与质量弹簧模型的谐振频率结果一致。当固定刚度和传动刚度均为5×108N/m和1×109N/m时(见图16和图18)，系统阶跃响应只在冲击力存在时有小幅值的振荡，且两种刚度值对系统阶跃响应影响差别很小。故建议把EMA的安装结构和传动结构的刚度设计在108N/m量级。

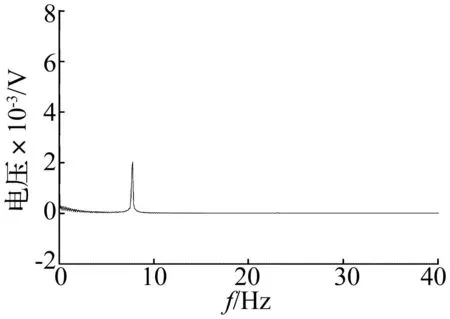
图17　固定刚度和传动刚度均为1×107 N/m时系统振荡频谱图Fig.17 EMA spectrogram when anchorage compliance and transmission compliance are 1×107 N/m

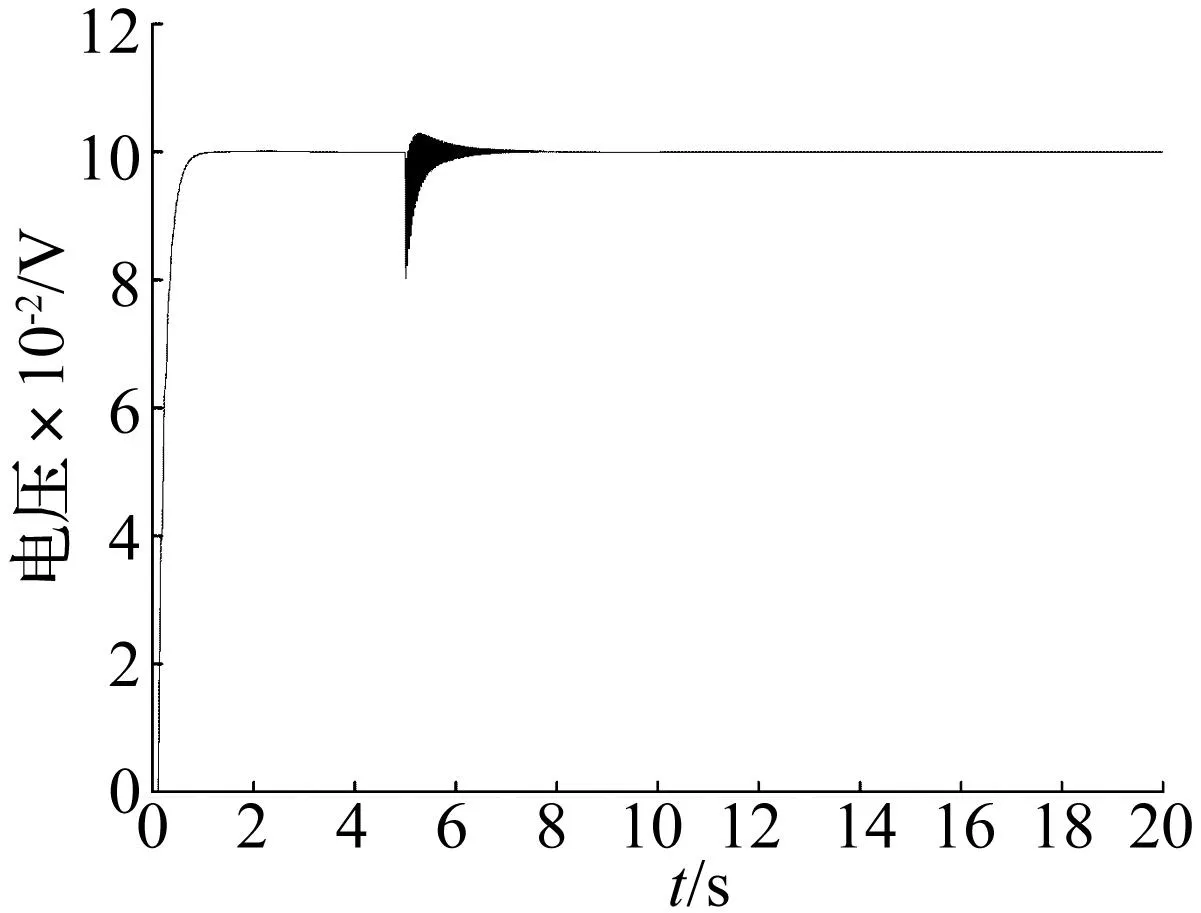
图18　固定刚度和传动刚度为1×109 N/m时系统阶跃响应Fig.18 EMA step response when anchorage compliance and transmission compliance are 1×109 N/m

另一方面，从图19～图22可知，当传动刚度为1×107N/m时，提高固定刚度可以明显提高系统的动态响应，而当固定刚度提高到1×109N/m时，已经和固定刚度为5×108N/m时的系统动态响应无明显区别。同样，当固定刚度为1×107N/m时，提高传动刚度也可以在一定程度上提高系统的动态响应，但即使当传动刚度为1×109N/m，系统的阶跃响应依然存在大范围的振荡。通过以上分析可知，固定刚度的提高对于系统动态响应的改善作用更明显。为保证EMA在工作过程中的信号跟踪能力，除采用必要的控制策略外，在结构方面应适当优先提高固定刚度。

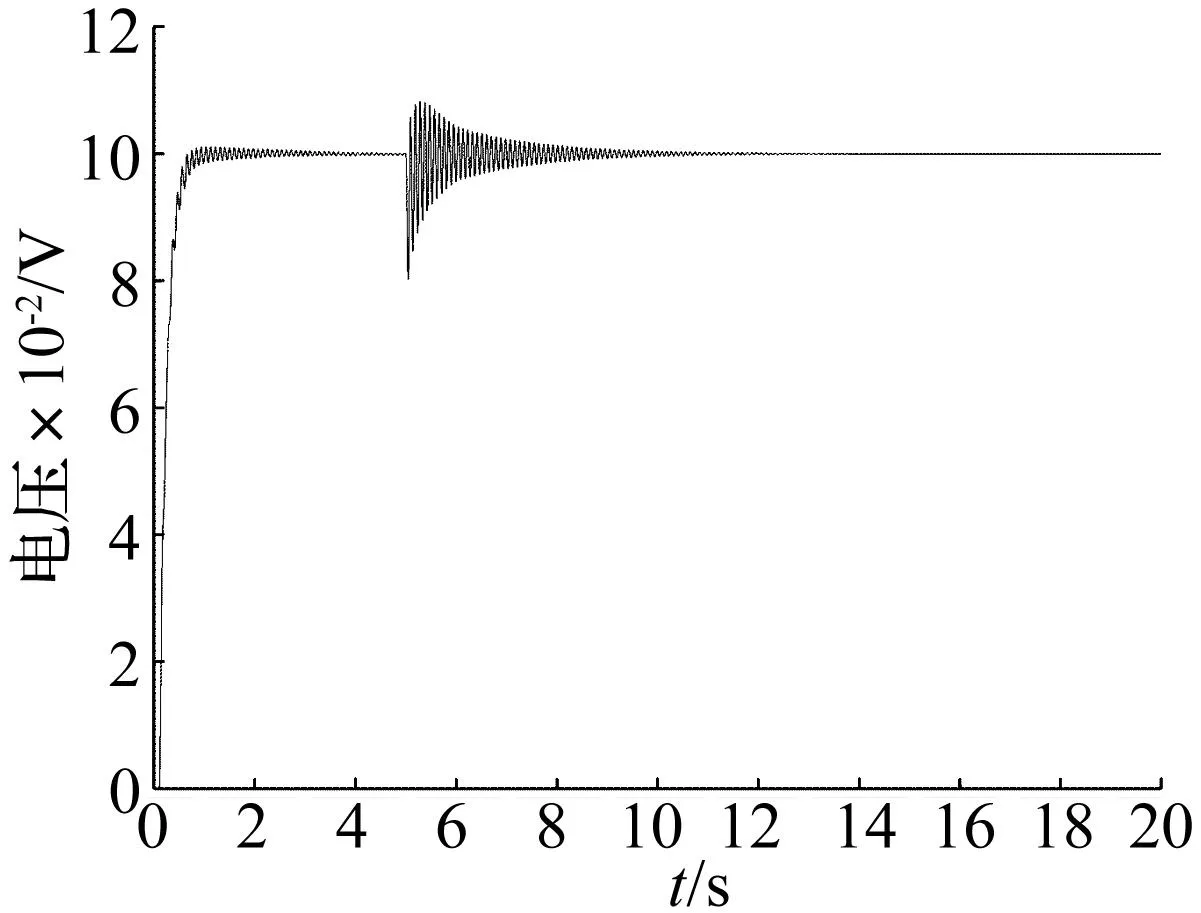
图19　固定刚度为5×108 N/m传动刚度为1×107 N/m时系统阶跃响应Fig.19 EMA step response when anchorage compliance is 5×108 N/m and transmission one is 1×107 N/m

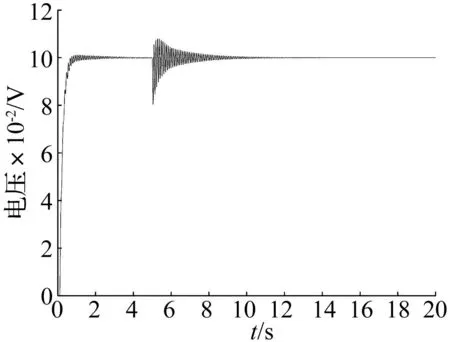
图20　固定刚度为1×109 N/m传动刚度为1×107 N/m时系统阶跃响应Fig.20 EMA step response when anchorage compliance is 1×109 N/m and transmission one is 1×107 N/m

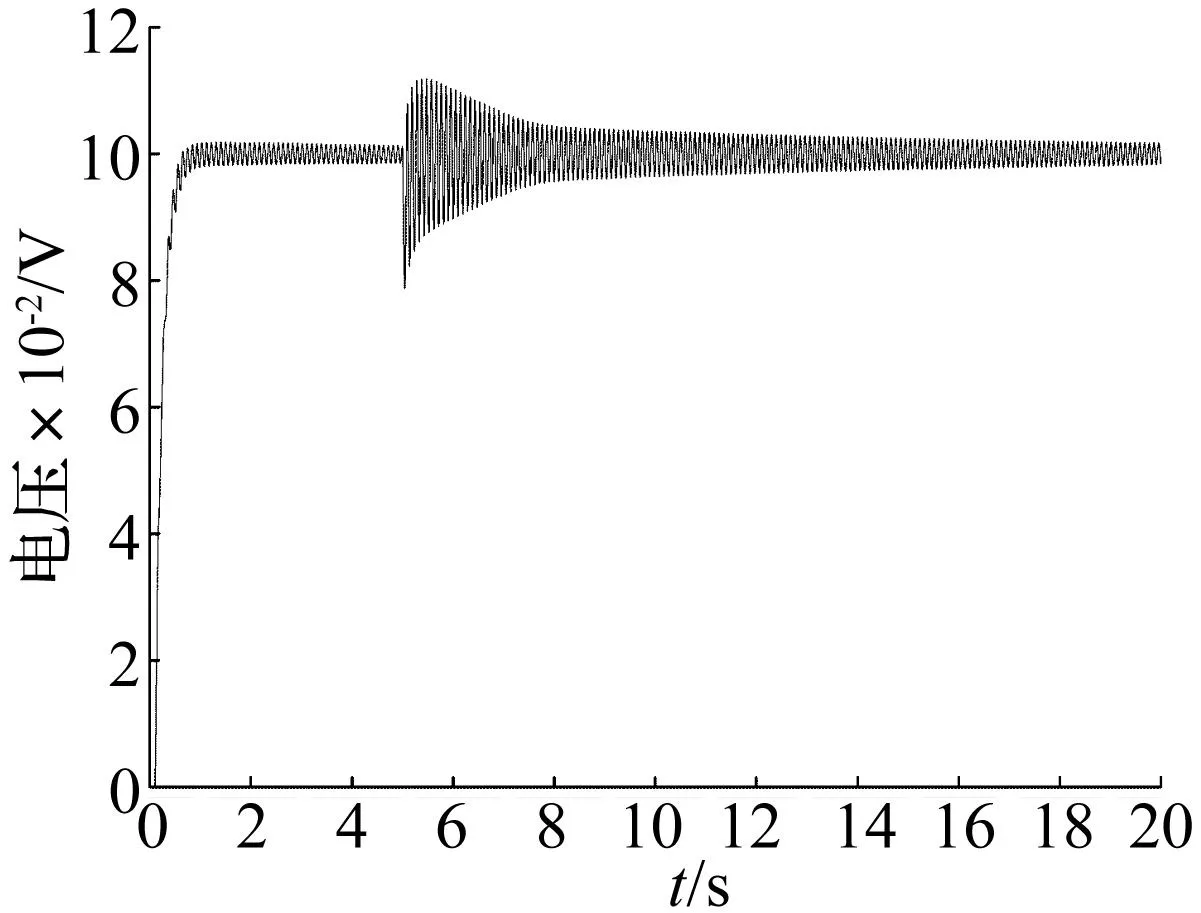
图21　固定刚度为1×107N/m传动刚度为5×108 N/m时系统阶跃响应Fig.21 EMA step response when anchorage compliance is 1×107 N/m and transmission one is 5×108N/m

图22　固定刚度为1×107N/m传动刚度为1×109 N/m时系统阶跃响应Fig.22 EMA step response when anchorage compliance is 1×107N/m and transmission one is 1×109N/m

3.4EMA系统动态仿真

根据EMA实际舵控经验，给定位移信号，参数如前述表1和表2，设置仿真时间为200 s，仿真步长为0.001 s，得到的仿真结果见图23。从图23～图24可知，系统的响应时间能够满足要求，系统动态跟踪性能良好。

图23　EMA仿真输出位移跟踪曲线Fig.23 Displacement response of EMA with simulation

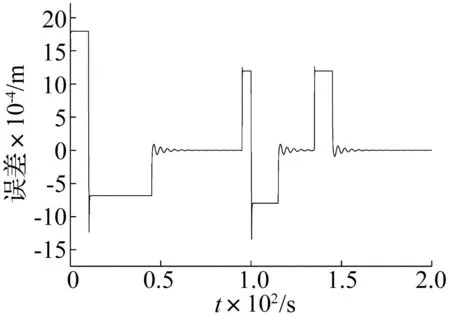
图24　位移跟踪误差曲线Fig.24 Displacement response error

在200 s的时间内，EMA的输出位移与给定位移信号的误差最大为1.8 mm，相对误差为1.2%，从而较好的反映了模型的有效性。同时，对比本文中EMA与文献[14]所述的传统阀控液压作动器，在给定相同舵控指令下，这两种作动器都能跟踪给定位移信号，但就跟踪效果而言，传统的阀控液压作动器要优于EMA，这也正是目前液压作动器存在的主要原因。然而，在重量、体积、系统效率和可维护性等方面，EMA有绝对优势。

4结论

采用AMESim图形化建模方法，建立了基于PRSM的EMA模型，对其在舵回路系统中的动态特性进行了仿真分析，得出以下结论：

(1) 传动间隙和摩擦特性是限制系统精度和稳定性的重要非线性影响因素。间隙的存在使得系统振荡不利于快速稳定，间隙量越大，系统的阶跃响应波动幅值越明显；PRSM中的摩擦使得系统存在静态误差，可通过力闭环反馈减小其对系统的影响。

(2) 固定刚度和传动刚度对EMA动态阶跃特性有不同程度的影响，建议把安装结构和传动结构的刚度设计在108N/m的量级；通过对比可知，固定刚度的提高对于系统动态响应的改善作用更明显，在结构设计方面应适当优先提高固定刚度。

(3) 在给定舵控指令下，机电作动器的仿真位移输出响应误差最大为1.8 mm，相对误差为1.2%，从而反映了模型的有效性。

参 考 文 献

[ 1 ] Jensen S C, Jenney G D, Dawson D.Flight test experience with an electromechanical actuator on the F-18 systems research aircraft [R]. NASA, 1998.

[ 2 ] DominiqueV D B. The A380 flight control electro-hydrostatic actuators, achievements and lessons learnt[C]//25th International Congress of the Aeronautical Sciences (ICAS), Sep. 5th, 2006.

[ 3 ] Karam W, Mare J C. Modeling and simulation of mechanical transmission in roller-screw electro-mechanical actuators[J]. Aircraft Engineering and Aerospace Technology, 2009, 81(4):288-298.

[ 4 ] Karam W, Mare J C. Force control of a roller-screw electromechanical actuator for dynamic loading of aerospace actuators[C]//Fluid Power and Motion Control Conference, Bath, 2008.

[ 5 ] Mare J C. Dynamic loading systems for ground testing of high speed aerospace actuators[J]. Aircraft Engineering and Aerospace Technology, 2006, 78(4): 275-282.

[ 6 ] Liscou⊇t J, Budinger M, Mare J C, et al. Modelling approach for the simulation-based preliminary design of power transmissions[J]. Mechanism and Machine Theory, 2011, 46(3): 276-289.

[ 7 ] Habibi S, Roach J, Luecke G. Inner-loop control for electro-mechanical (EMA) flight surface actuation systems[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2008, 130: 051002-1-13.

[ 8 ] 齐海涛, 付永领. 基于AMESim的电动静液作动器的仿真分析[J]. 机床与液压, 2007, 35(3): 184-186.

QI Hai-tao, FU Yong-ling. Simulation of electro-hydrostatic actuator based on AMESim[J]. Machine Tool and Hydraulics, 2007, 35(3): 184-186.

[ 9 ] 马尚君, 刘更, 周建星, 等. 行星滚柱丝杠副运转过程动态特性分析[J]. 振动与冲击, 2013, 32(3): 167-171.

MA Shang-jun, LIU Geng, ZHOU Jian-xing,et al. Dynamic characteristic analysis of a planetary roller screw in operating process[J]. Journal of Vibration and Shock, 2013, 32(3): 167-171.

[10] 周元钧, 赵运坤, 葛云海. 复合式余度机电作动系统容错控制与性能分析[J]. 北京航空航天大学学报, 2008, 34(3): 285-289.

ZHOU Yuan-jun, ZHAO Yun-kun, GE Yun-hai. Fault-tolerant control method and characteristic analysis of hydraulic redundant EMA system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(3): 285-289.

[11] 付永领, 齐海涛, 王利剑, 等. 混合作动系统的工作模式研究[J]. 航空学报, 2010, 31(6): 1177-1184.

FU Yong-ling, QI Hai-tao, WANG Li-jian, et al. Research on operating modes in hybrid actuation systems[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1177-1184.

[12] Nordin M, Galic J, Gutman P. Newmodels for backlash and gear play[J]. Int. J. Adapt. Control Signal Process., 1997, 11: 49-63.

[13] 王占林. 液压伺服控制[M]. 北京: 北京航空学院出版社, 1987.

[14] 齐海涛, 付永领, 祁晓野. 一体化数字液压作动系统的建模仿真和控制[J]. 北京航空航天大学学报, 2014, 40(1): 44-47.

QI Hai-tao, FU Yong-ling, QI Xiao-ye. Modelling, simulation and control of integrated digital hydraulic actuation system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(1): 44-47.

Dynamic characteristic analysis for an electro-mechanical actuator based on planetary roller screw mechanism

QIAOGuan,LIUGeng,MAShang-jun,TONGRui-ting,ZHOUYong(Shaanxi Provincial Engineering Laboratory for Transmissions and Controls, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:Aiming at an electro-mechanical actuator (EMA) in an actuator loop, a model of EMA based on a planetary roller screw mechanism (PRSM) was developed to investigate the effects of nonlinearities associated with structural stiffness, friction and clearance on the dynamic characteristics of the EMA system. Anchorage compliance and transmission compliance related to aerodynamic force were considered. The simulation analysis results with AMESim showed that the improvement of anchorage compliance has a more important influence on the system’s transient response than that of transmission compliance does; the fluctuation of the system’s step response becomes more obvious with a bigger clearance in the PRSM; besides, under a certain input command, the maximum displacement output error of EMA is 1.8mm and the relative error is 1.2%. The nonlinear model was proved to be an effective one which provided a theoretical foundation for the further structural optimization and control of EMA.

Key words:electro-mechanical actuator; planetary roller screw mechanism; dynamic characteristic; structural stiffness; clearance nonlinearity

中图分类号:TH132.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.013

通信作者刘更 男，博士,教授，博士生导师，1961年生

收稿日期：2014-11-14修改稿收到日期：2015-04-20

基金项目：中国博士后科学基金(2014M552483)；国家自然科学基金(51275423, 51207129)；教育部高等学校博士学科点专项科研基金(20126102110019)；高等学校学科创新引智计划(B13044)

第一作者 乔冠 男，博士生，1990年生