基于KSLPP与RWKNN的旋转机械故障诊断
王雪冬, 赵荣珍, 邓林峰(兰州理工大学 机电工程学院,兰州 730050)
基于KSLPP与RWKNN的旋转机械故障诊断
王雪冬, 赵荣珍, 邓林峰(兰州理工大学 机电工程学院,兰州730050)
摘要:针对旋转机械高维故障特征集识别精度低的问题,提出基于核监督局部保留投影(Kernel Supervised Locality Preserving Projection, KSLPP)与ReliefF特征加权的K近邻(ReliefF Weighted K-Nearest Neighbor, RWKNN)分类器相结合的维数约简故障诊断方法。该方法首先应用KSLPP提取故障特征集中的非线性信息,同时在降维投影过程中充分利用类别信息,使降维后最小化类内散度,最大化类间分离度;随后,将降维后得到的低维敏感特征集输入RWKNN进行模式识别,RWKNN能够突出不同特征对分类的贡献率,强化敏感特征,弱化不相关特征,提升了分类精度和鲁棒性。最后,通过典型转子实验台的故障特征集验证了该方法的有效性。
关键词:故障诊断;核监督局部保留投影;ReliefF特征选择;加权K近邻分类器
在进行复杂旋转机械故障诊断时,为了获得较高的诊断精度,就必须获取尽可能多的故障信息[1]。此时基于多通道、多域(时域、频域及时频域)的故障诊断模式具有较强优势。然而,该模式在获得有效信息的同时还将引入大量的非敏感及干扰特征,无疑会增加分类器学习、训练的时间及空间复杂度,甚至降低分析处理的精度[2]。因此如何获取低维敏感特征子集的数据降维问题已成为基于数据驱动故障诊断的一个重要研究方向。
局部保留投影(Locality Preserving Projection, LPP)作为流形学习中的一种线性算法,既解决了主元分析(Principal Component Analysis, PCA)、Fisher判别分析(Fisher Discriminant Analysis, FDA)等传统降维方法难以保持原始数据非线性流形的缺点,又解决了非线性流形学习方法难以获得新样本点低维投影的缺点,因而得到了广泛的应用[3-4]。但LPP本质是一种线性无监督算法,面对数据集的非线性及各类别特征不明显等问题时,不能获取具有强辨识力的低维矢量。针对该问题,文献[5]提出了一种有监督的LPP算法(Supervised Locality Preserving Projection, SLPP),该算法在降维投影时会根据类别信息使同类别尽可能靠近,不同类别尽可能远离。进一步地,通过引入核方法,可将核监督局部保留投影(Kernel Supervised Locality Preserving Projection, KSLPP)的作用范围引入到非线性领域。目前,KSLPP的相关算法已在图像识别领域取得了很好的应用效果[6-7]。故如能将KSLPP应用到旋转机械高维、非线性故障数据集的降维问题中,则对于发展旋转机械的智能诊断具有重要意义。
为实现KSLPP降维后低维矢量与故障类型间的快速识别,需选择出一种简单、高精度的智能分类器。K近邻(K-Nearest Neighbor, KNN)分类器[8]作为一种非参数分类方法,以其简单直观,分类特性好,时效性强等优点,在故障诊断方面得到了广泛应用[9-10]。但KNN在分类时易受不良特征的干扰、不能突出敏感特征在分类时的贡献率等缺点,导致故障诊断精度难以进一步提升。ReliefF作为公认效果较好的过滤式特征评估算法[11],具有较高评估效率以及对数据类型没有限制等优点,其算法原理是根据属性特征在同类样本以及相近的不同类样本的区分能力进行评估得到相应的权值,权值越大表明该特征与该类间的相关度越高。因此若能将ReliefF特征选择后的权值引入到KNN中进行加权,无疑会很大程度上提升KNN的识别能力。
基于上述说明,本文欲借助KSLPP针对非线性数据集维数约简的能力以及ReliefF特征加权KNN(ReliefF Weighted K-Nearest Neighbor, RWKNN)在分类识别上的优势,将上述两种算法应用于旋转机械故障数据集的智能分类,欲为基于海量故障数据资源挖掘的智能故障辨识技术的发展提供参考依据。
1KSLPP算法
SLPP是基于LPP改进的一种降维方法,该算法的基本思想是保留类内局部结构的同时最大化类间分类度[5]。KSLPP则是通过引入式(1)所示的高斯核函数,将SLPP的应用扩展到非线性领域。
式中,xi,j∈X(X={xi|i=1,2,…,n,xi∈Rd}),Ф表示非线性函数,σ表示核参数。
KSLPP定义的目标函数如式(2)所示:
(2)
式中,yi,j∈Y(Y={yi|i=1,2,…,n,yi∈Rl}),且Y=aTФ(X),a为投影向量。式(3)表示了目标函数简单的变换过程
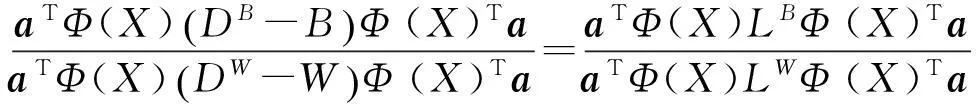
式中,LB=DB-B,LW=DW-W,DB和DW都是对角矩阵,DB为类间相似度矩阵B(见式(5))对应的列或行元素的和,DW为类内相似度矩阵W(见式(6))对应的列或行元素的和。式(3)转换成广义特征值问题见式(4),即
KLBKTa=λKLWKTa
(4)
1.1KSLPP算法流程
步骤1将观测矩阵X进行数据归一化,得到Xb。
步骤2将Xb通过核函数K(·)映射到高维特征空间H,得到Ф(Xb)。
步骤3通过k近邻法对数据集Ф(Xb)构造类内、类间邻接图。设G表示有n个节点的邻接图,第i个节点与Ф(xi)对应,分别在类内和类间寻找与其相近的k个近邻Ф(xj),并连接节点i和j。
步骤4计算类间权重矩阵B和类内权重矩阵W见式(5)和(6)
(5)
(6)
式中,Sij为相似性矩阵S中的元素,计算Sij的公式见式(7)
(7)
式中,t为常数。
步骤5由式(4)求解广义特征值和特征向量。得到特征值λ1,λ2…,λH(按降序排列)及特征向量a1,a2…, aH。选取其中前l个最大特征值对应的特征向量,得到投影向量a={a1,a2…,al},并将Ф(Xb)通过a进行降维投影,得到低维特征集Y见式(8)。
Y=aTΦ(Xb)
(8)
2ReliefF特征加权的KNN分类器
RWKNN是对一般KNN算法的扩展,解决了KNN算法在分类时会将各特征属性同等权重,不能突出敏感特征在分类过程中的贡献率的缺点。RWKNN算法可描述如下:
对于任意一个训练样本xi∈X(X={xi|i=1,2,…,n,xi∈Rd})其类别属性为ci∈C={i=1,2,…,b},首先从和xi同类的样本集中找出k个近邻样本实例Hj(j=1,2,…,k),然后再从xi不同类的样本集中找出k个最近邻样本实例Mj(C)(j=1,2,…,k,C≠class(xi)),得到特征权重的递推公式见式(9)
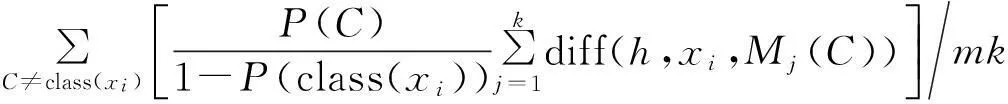
(10)
对于离散特征
(11)
循环m次后,可得到每个特征所对应的均值权重W(h)。该值越大,表明该特征对类分离度贡献越大,越小表明则表明该特征对类分离度贡献越小,据此可分析出各特征对分类的影响程度。
计算测试样本xt与每个训练样本特征xi距离见式(12)
(12)
式中,W(h)表示当特征为h时基于ReliefF特征选择的权重见式(9)。
选取与测试样本最近距离的k个训练样本,然后基于这k个样本的类别ci判断给出xt最有可能的类别ct,并使得分类目标误差Mi最小。
(13)
式中,P(ct/xt)表示样本xt分类为ct的概率,R(ct,ci,)表示将ct分类为ci产生的误差见式(14)
(14)
RWKNN与KNN算法一样都不能给出测试样本xt的精确分类,而是给出最有可能的所属类别即
(15)
式中,RWKNN(xt)就对应测试样本xt的分类结果。
2.1RWKNN识别流程
RWKNN算法的识别流程见图1,主要分为两步:① 基于ReliefF特征选择算法计算出训练样本集每个特征的权值,组成权值矩阵W;② 将W训练样本集和测试样本输入加权KNN进行分类识别,得出测试样本的类别。

图1 RWKNN识别过程Fig.1 Identification process of RWKNN
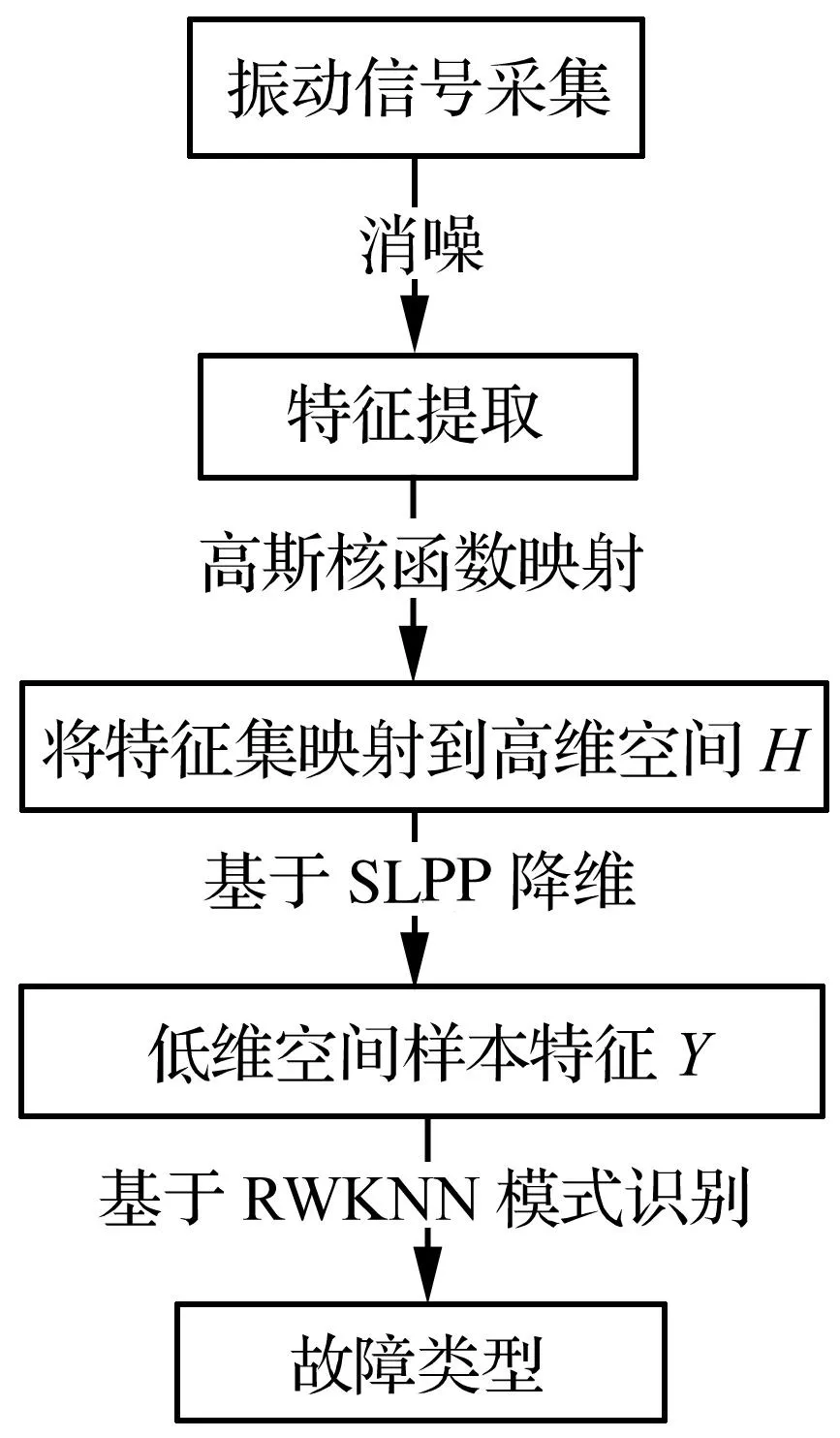
图2 基于KSLPP与RWKNN的故障诊断流程图Fig.2 Procedure of fault diagnosis based on KSLPP and RWKNN
3基于KSLPP与RWKNN的故障诊断方法
基于KSLPP与RWKNN设计的故障诊断流程如图2所示。由于1.1节和2.1节分别对KSLPP降维过程和RWKNN的识别过程做了描述,本节只对整个故障诊断的流程及具体需要注意的问题进行说明。整个故障诊断流程由如下几个步骤组成:对消噪后的振动信号作时域、频域和时频域的特征提取,得到原始数据特征集X;根据故障数据的具体特性确定核参数σ,并将特征集经高斯K(·)映射到高维特征空间H,在此空间基于SLPP降维,得到低维特征集Y;将低维特征集Y输入RWKNN进行模式识别,得到测试样本的故障类型。
4实验方法和结果
本项工作的研究对象为图3所示的转子实验台[12],在该试验台上分别模拟了四种故障状态(动静碰磨、转子不对中、质量不平衡、轴承松动)以及正常状态转动实验。在采样频率为10 kHz,转速为3 500 r/min的情况下,采集每种状态各40组样本,选取其中25组作训练集,15组作测试集。并针对样本集中每一通道(共12通道)的振动信号选取如表1的特征集合,共得到12×35=420个特征。由于该特征集含有大量干扰及不敏感特征,因此需要通过特征选择算法进行特征选择。本文参考文献[13]中的类间可分性算法去除原始特征集的无关特征,选取其中可分性指标大于1.0的特征,共得到116个利于降维分类的敏感特征。
由实验可知,在应用KSLPP算法对特征数据集降维时,高斯核参数的选取对最后的分类结果有很大影响。当参数为3.0~6.0时识别效果相对较好,而大于6.0及小于3.0时效果则会越来越差。本文取其值为4.0,得到测试样本降维效果如图3(f)所示(图3中“◆”、“○”、“☆”、“△”、“+”分别表示正常、不平衡、不对中、松动、碰磨)。为了使实验更具说服力,本文分别应用了PCA、FDA、KPCA、LPP、SLPP等方法对故障特征集进行降维处理,测试样本降维效果如图3(a)~图3(e)所示。从图3中可以看出:基于PCA提取的低维特征在两个维度情况下具有最差的判别能力,除了松动故障,其他四种故障混淆在一起;而利用核映射的有监督方法KSLPP,五种故障在两个维度情况下,类间间距明显,类内距离小。
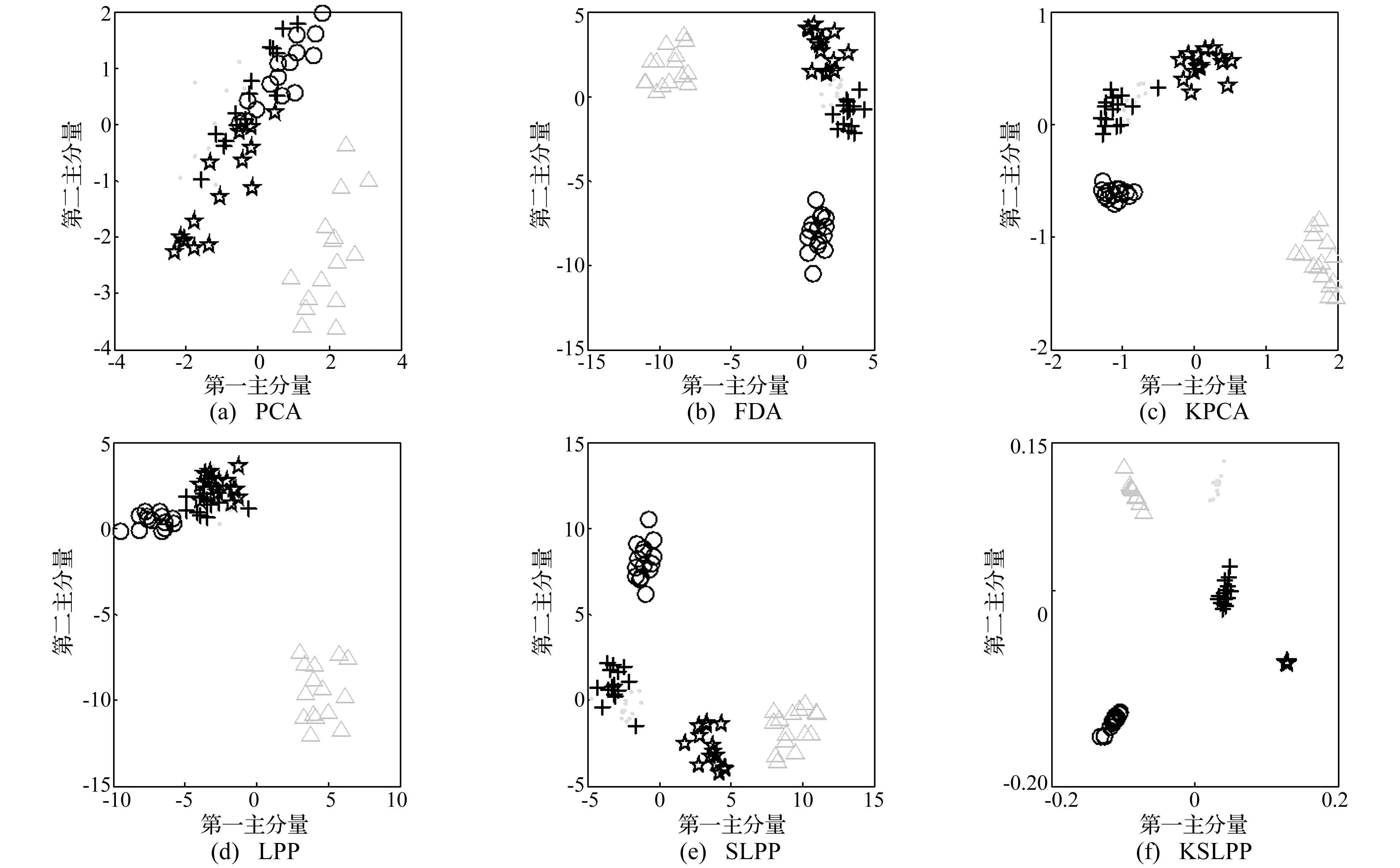
图3 测试样本基于不同方法的降维结果Fig.3 Test sample based on different dimension reduction method results
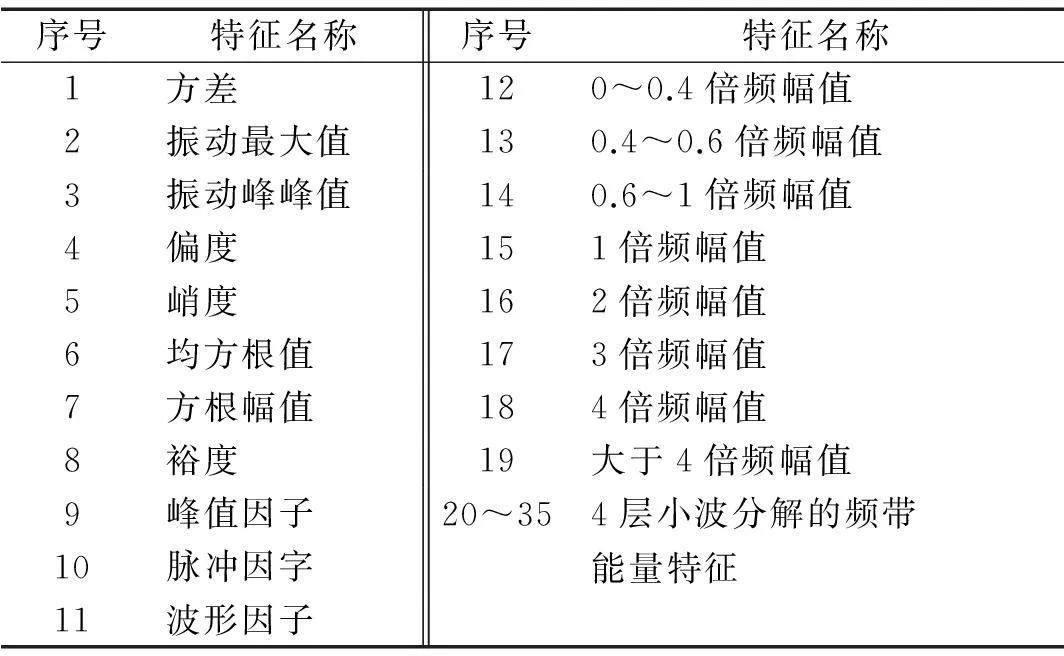
序号特征名称序号特征名称1方差120~0.4倍频幅值2振动最大值130.4~0.6倍频幅值3振动峰峰值140.6~1倍频幅值4偏度151倍频幅值5峭度162倍频幅值6均方根值173倍频幅值7方根幅值184倍频幅值8裕度19大于4倍频幅值9峰值因子20~354层小波分解的频带10脉冲因字能量特征11波形因子
注:1~11为时域特征;12~19为频域特征[14];20~35为时频域小波能量特征。
为了量化描述上述方法的降维效果,本文将得到六种方法的低维敏感特征集输入RWKNN进行模式识别,得到的识别率见表2。从表中可以看出:① 有监督的方法FDA、SLPP、KSLPP降维后的识别正确率要明显优于无监督的PCA、LPP、KPCA,这是因为利用类别标签的有监督降维方法找寻的是具有判别力的低维特征而非表征特征集的描述特征;② FDA的识别率要低于SLPP,原因是FDA和PCA一样是为了尽可能保持样本的全局结构,而忽略了更能反映状态类型的局部结构;③ 经KSLPP降维后基于RWKNN识别效果极佳,各状态都达到了100%正确率,这是因为利用核映射能将特征集中的非线性问题转化为线性问题,再通过基于局部结构出发的有监督算法SLPP,能够找寻到最有辨识力的低维敏感特征。
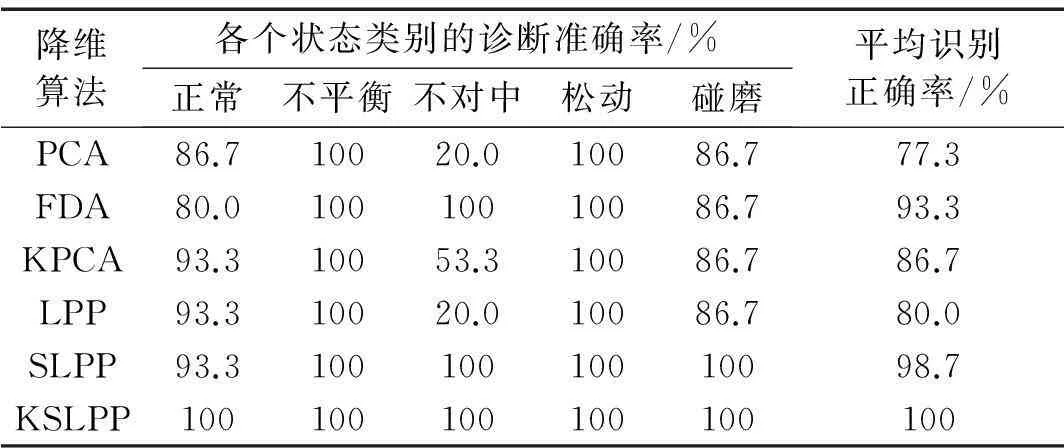
表2 降维算法及其RWKNN辨识准确率
为验证RWKNN的鲁棒性,本文采用文献[15]的方法首先将混合域故障特征集融入系数a=0.1、0.2、0.3的随机干扰噪声,然后通过KSLPP降维,最后将得到的低维特征集输入RWKNN、KNN和SVM进行故障模式识别,得到的平均识别率见表3。由表中可以看出:① KNN的识别率要优于SVM,原因是SVM受核函数的影响很大,在没有对核函数进行复杂的优化建模条件下,SVM的识别率无法达到最优;② 即使原始特征集有一定的干扰,基于权重系数调整特征贡献率的RWKNN方法诊断仍然能获得极高的识别正确率,由此证明了RWKNN具有较强的抗干扰性,较高的识别精度等优点。
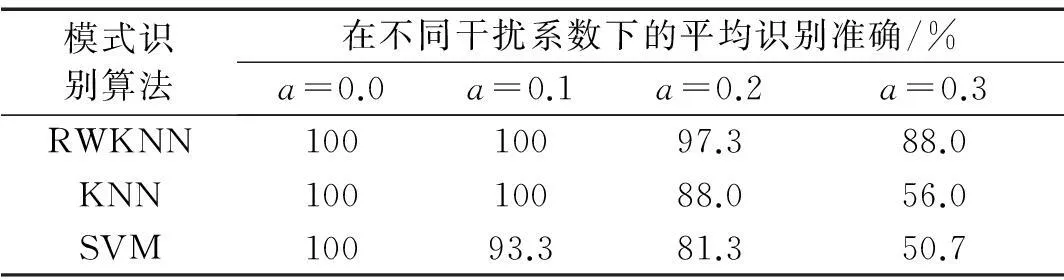
表3 不同模式识别算法的抗干扰能力对比
5结论
(1) KSLPP不仅将LPP引入到了非线性领域,同时也避免了LPP降维过程中对类内局部结构和类间分离性的忽略,使得低维空间投影能够有效保持高维流形的局部几何结构。
(2) RWKNN能够针对不同特征对分类的敏感程度给出权重系数,权重系数越大的特征在分类时贡献率越高,保证了在分类识别时的识别精度和泛化能力。
(3) 基于KSLPP和RWKNN相结合的维数约简故障诊断模式,发挥了多通道、多域在故障信息的全方面构造、KSLPP在数据降维和RWKNN在类别辨识上的优势。通过转子实验台故障数据集的实验结果表明,该诊断模式具有较强的泛化能力,较高的识别精确度等优点,为复杂旋转机械故障诊断的智能化诊断提供了一条新的解决思路。
参 考 文 献
[ 1 ] 苏祖强, 汤宝平, 姚金宝. 基于敏感特征选择与流形学习维数约简的故障诊断[J].振动与冲击, 2014, 33(3): 70-75.SU Zu-qiang, TANG Bao-ping, YAO Jin-bao. Fault diagnosis method based on sensitive feature selection and manifold learning dimension reduction[J].Journal of Vibration and Shock, 2014, 33(3): 70-75.
[ 2 ] 梁胜杰, 张志华, 崔立林, 等. 基于主成分分析与核独立成分分析的降维方法[J].系统工程与电子技术, 2011, 33(9): 2144-2148.
LIANG Sheng-jie, ZHANG Zhi-hua, CUI Li-lin, et al. Dimensionality reduction method based on PCA and KICA[J].Systems Engineering and Electronics, 2011, 33(9): 2144-2148.
[ 3 ] He Xiao-fei, Niyogi P. Locality Preserving Projections[C]//Advances in Neural Information Processing Systems. Cambridge, USA: MIT Press, 2004, 16: 153-160.
[ 4 ] 张志伟, 杨帆, 夏克文, 等. 一种有监督LPP算法及其在人脸识别中的应用[J].电子与信息学报, 2008, 30(3): 539-541.
ZHANG Zhi-wei, YANG Fan, XIA Ke-wen, et al. A supervised LPP algorithm and its application to face recognition[J].Journal of Electronics & Information Technology, 2008, 30(3): 539-541.
[ 5 ] 申中华, 潘永惠, 王士同. 有监督的局部保留投影降维算法[J].模式识别与人工智能, 2012, 23(2): 233-239.
SHEN Zhong-hua, PAN Yong-hui, WANG Shi-tong. A supervised locality preserving projection algorithm for dimensionality reduction[J].Pattem Recognition and Aitificial Intelligence, 2012, 23(2): 233-239.
[ 6 ] 祝磊, 朱善安. KSLPP:新的人脸识别算法[J].浙江大学学报:工学版, 2007, 41(7): 1065-1069.
ZHU Lei, ZHU Shan-an. KSLPP:new algorithm for face recognition[J].Journal of Zhejiang University:Engineering Science, 2007, 41(7): 1065-1069.
[ 7 ] Cheng Jian, Liu Qing-shan, Lu Han-qing, et al. Supervised kernel locality preserving projections for face recognition[J].Neurocomputing, 2005,67: 443-449.
[ 8 ] Songbo T. An effective refinement strategy for KNN text classifier[J].Expert Systems with Applications, 2006, 30: 290-298.
[ 9 ] 李锋, 汤宝平, 陈法法. 基于线性局部切空间排列维数化简的故障诊断[J].振动与冲击, 2012, 31(13): 36-40.
LI Feng, TANG Bao-ping, CHEN Fa-fa. Fault diagnosis model based on dimension reduction using linear local tangent space alignment[J].Journal of Vibration and Shock, 2012, 31(13): 36-40.
[10] Pandya D H, Upadhyay S H, Harsha S P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN[J].Expert Systems with Applications, 2013,40(10): 4137-4145.
[11] Kononenko I. Estimation attributes: Analysis and extensions of RELIEF[C]// Proceedings of the 1994 European Conference on Machine Learning. Catania: Springer Verlag, 1994: 171-182.
[12] 霍天龙, 赵荣珍, 胡宝权. 基于熵带法与PSO优化的SVM转子故障诊断[J].振动、测试与诊断, 2011, 31(3): 279-284.
HUO Tian-long, ZHAO Rong-zhen, HU Bao-quan. Fault diagnosis for rotor systems based on entropy Band method and support vector machine optimized by PSO[J].Journal of Vibration, Measurement & Diagnosis,2011,31(3): 279-284.
[13] 杨艺, 韩德强, 韩崇昭. 基于排序融合的特征选择[J].控制与决策, 2011, 26(3): 397-401.
YANG Yi, HAN De-qiang, HAN Chong-zhao. Study on feature selection based on rank-level fusion[J].Control and Decision, 2011, 26(3): 397-401.
[14] 于达仁, 胡清华, 鲍文. 融合粗糙集和模糊聚类的连续数据知识发现[J].中国电机工程学报, 2004, 24(6): 205-210.
YU Da-ren, HU Qing-hua, BAO Wen. Combining rough set methodolgy and fuzzy clustering for knowledge discovery from quantitative data[J].Proceedings of the CSEE,2004,24(6):205-210.
[15] 陈法法, 汤宝平, 马婧华, 等. 基于遗传退火优化MSVM的齿轮箱故障诊断[J].振动、测试与诊断, 2014, 34(4): 699-704.
CHEN Fa-fa, TANG Bao-ping, MA Jing-hua, et al. Gearbox fault diagnosis based on multi-kernel support vector machine optimized by genetic simulated annealing algorithm[J].Journal of Vibration, Measurement & Diagnosis,2014,34(4): 699-704.
Rotating machinery fault diagnosis based on KSLPP and RWKNN
WANGXue-dong,ZHAORong-zhen,DENGLin-feng(School of Mechanical and Electronical Engineering of Lanzhou University of Technology, Lanzhou 730050, China)
Abstract:Aiming at the questions of high dimension and low precision of the recognition of rotating machinery fault diagnosis, an intelligent fault diagnosis method based on kernel-supervised locality preserving projection and K-nearest neighbor weighted by feature selection ReliefF algorithm (RWKNN) was proposed.KSLPP can effectively extract nonlinear information in an original feature data set and at the same time make full use of class information in dimension-reduction projection, and make the sample minimize the within-class dispersion and maximize the separation between classes.Then, the sensitive low-dimension feature data set is fed into the K-nearest neighbor weighted by feature selection ReliefF algorithm to recognize the fault type.RWKNN can highlight the contribution rate of different features for classification, strengthen sensitive characteristics, weaken irrelevant features and improve the classification accuracy and robustness.Finally, the validity of the proposed method was verified by the typical rotor fault vibration signal.
Key words:fault diagnosis; kernel-supervised locality preserving projection (KSLPP); feature selection ReliefF; weighted K-nearest neighbor
中图分类号:TP18; TH165
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.08.035
通信作者赵荣珍 女,博士,教授,博士生导师,1960年12月生
收稿日期:2014-12-05修改稿收到日期:2015-04-27
基金项目:高等学校博士学科点专项科研基金(20136201110004)
第一作者 王雪冬 男,硕士生,1988年12月生

