机械密封端面接触状态的声发射监测研究

李晓晖， 傅　攀， 曹伟青， 陈　侃(.西南交通大学 机械工程学院，成都　6003； .四川日机密封件股份有限公司，成都　6004)



机械密封端面接触状态的声发射监测研究

李晓晖1， 傅攀1， 曹伟青1， 陈侃2(1.西南交通大学 机械工程学院，成都610031； 2.四川日机密封件股份有限公司，成都610041)

摘要：有效监测机械密封的端面接触状态有助于对密封失效做出早期预警。针对密封声发射信号难以降噪的问题，提出基于神经网络粒子滤波和最小二乘支持向量机的声发射建模方法。首先通过机械密封的端面膜厚测量，研究声发射能量在密封启动过程中的变化规律；接着利用人工神经网络构建信号的状态空间，再通过粒子滤波算法对状态空间滤波降噪；最后从滤波信号中提取特征，并利用最小二乘支持向量机构建机械密封端面接触状态的检测模型。实验数据证明该方法能有效实现机械密封端面状态的无损检测，具有良好的工业前景。

关键词：密封端面接触；声发射；粒子滤波；状态监测；最小二乘支持向量机

流体动压型机械密封是一类非接触式机械密封，它主要通过密封端面之间的流体膜来实现润滑与密封的作用[1]。然而密封刚启动时，由于动压效应不足，流体膜还不能形成，因此密封副之间存在着显著的接触与摩擦。这种摩擦将产生大量的力和热，并对密封端面造成持续的划伤与磨损，从而减少密封的使用寿命。由此可见，有效监测机械密封的端面接触状态，将有助于对密封失效做出早期预警。

最直接的方法是直接对密封膜厚进行检测，而长期以来，已有不少学者致力于该项内容的研究。较早时，Astridge等[2-3]便通过电阻和电容的方式对密封膜厚进行了测量，而Etsion等[4]也证实了电涡流检测的有效性；然而，以上方法均须对密封结构进行改造，以便于传感器的安装，因此只适用于实验研究。后来，Anderson等[5-6]采用超声波检测技术，通过分析信号的幅值变化来对密封膜厚进行估计；然而，由于该方法的监测成本过于昂贵，因此仍不适宜推广到工业现场。

作为一种成本较低的无损检测技术，声发射检测对于机械密封有着良好的工业前景。Williams等[7-8]对此进行了研究，并取得了一定的成果；然而由于声发射对环境噪声过于敏感，因此实践中往往难以实现良好的信噪分离。高志等[9]研究了机械密封在启动过程中的声发射特征，并利用均方根来反映密封端面的摩擦强度；但他没能提出有效的信号降噪方法，也没有建立起监测密封端面接触状态的数学模型。Zhang等[10]从摩擦学的角度对密封的端面接触进行了阐述，并通过经验模态分解和Laplace小波变换来对所测信号进行处理；然而流体膜未成型时，信号的频谱结构并不稳定，因此该方法难以检测出密封端面的开启瞬间。为了抑制密封信号的随机波动，李晓晖等[11]提出了基于核主分量分析和联级神经网络的声发射建模方法；然而由于缺乏对密封噪声特征的研究，因此该方法具有一定的盲目性和随机性。

本文主要研究密封开启过程中的声发射特征，并针对密封信号难以降噪的问题，提出基于神经网络粒子滤波(Particle Filter with Artificial Neural Network, ANN-PF)和最小二乘支持向量机(Least Square Support Vector Machine, LS-SVM)的声发射处理算法。首先利用Elman ANN建立信号的状态空间，再通过PF对状态空间滤波降噪，最后利用LS-SVM建立密封端面接触状态的识别模型。实验数据证明，该方法能有效监测机械密封的端面接触状态，从而为密封失效的早期预警提供了良好的数据支撑。

1实验方案

实验以流体动压型机械密封为研究对象，以水为密封介质，其传感器安装方式见图1。

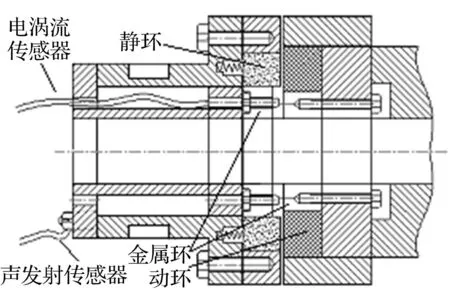
图1　传感器安装Fig.1 Sensors installation

图1中利用电涡流传感器直接测量膜厚，同时利用声发射传感器检测密封端面的摩擦强度。首先在密封的动静环内各镶嵌一个金属环，并将金属环与密封端面一齐磨平抛光；接着在静环内嵌的金属环上打通孔，并将电涡流传感器从小孔处伸入；最后将声发射传感器安装在密封腔的外壳。实验所用的电涡流传感器型号为KD2306，其分辨率为0.1 μm；声发射传感器的型号为8152B12SP，其有效检测频率为50～400 kHz。

实验的信号采集系统见图2。

图2　数据采集系统Fig.2 Data acquisition system

图2中电涡流信号经同型号的前置放大器放大，再由PCIe-6341型低频采集卡进行数据采集，其采样频率设为500 Hz；声发射信号经5125型前置放大器放大，再由PCI-6132型高频采集卡进行数据采集，其采样频率设为1 MHz。最后在工控机上通过Labview编程调用采集卡驱动，以实现上述信号的同步采集。

为区分密封端面信号和背景噪声，分别进行有密封和空转实验以作对比。具体操作步骤如下：①保持密封腔压力为0.5 MPa，启动透平机，使设备主轴转速匀速提升到1 500 r/min，并记录该过程中的电涡流和声发射数据；②重复步骤①，以获得多次重复采样数据；③卸下密封环，启动透平机，使设备主轴转速匀速提升到1 500 r/min，并记录该过程中的声发射数据。

2实验信号观测

根据所测数据，密封启动过程中的膜厚变化见图3。

图3　膜厚曲线Fig.3 Curves of film thickness

由图3知，密封刚启动时，所测膜厚值为0，说明密封端面仍保持接触，其摩擦形式为干摩擦。接着，约1.5 s之后，膜厚值陡然升高，说明密封端面在一瞬间开启。然而此时的液膜并不稳定，因此信号幅值往往存在剧烈的波动。而后，随着密封转速的不断增加，流体膜逐渐增厚，并最终稳定在4～5 μm内。在此期间，密封端面保持分离，其摩擦形式为流体摩擦。

在密封开启过程中，与膜厚所对应的声发射信号见图4。

图4　电涡流和声发射信号对比Fig.4 The comparison of the film thickness with the AE signal

根据图4，可将密封端面分为三种接触状态：① 端面接触状态：流体膜尚未形成，密封端面直接接触并产生干摩擦，因此声发射能量较强；② 端面开启状态：流体膜没有完全成型，密封端面随机接触并产生混合摩擦，从而导致声发射能量剧烈波动；③ 端面分离状态：流体膜完全形成，密封端面保持分离并形成流体摩擦，因此声发射能量减弱并保持相对稳定。

实验中，流体膜一般在200～300 r/min时形成，且端面开启状态不超过0.2 s。

为了研究背景噪声对密封信号的影响，图5给出了有密封和空转实验下的声发射能量对比。

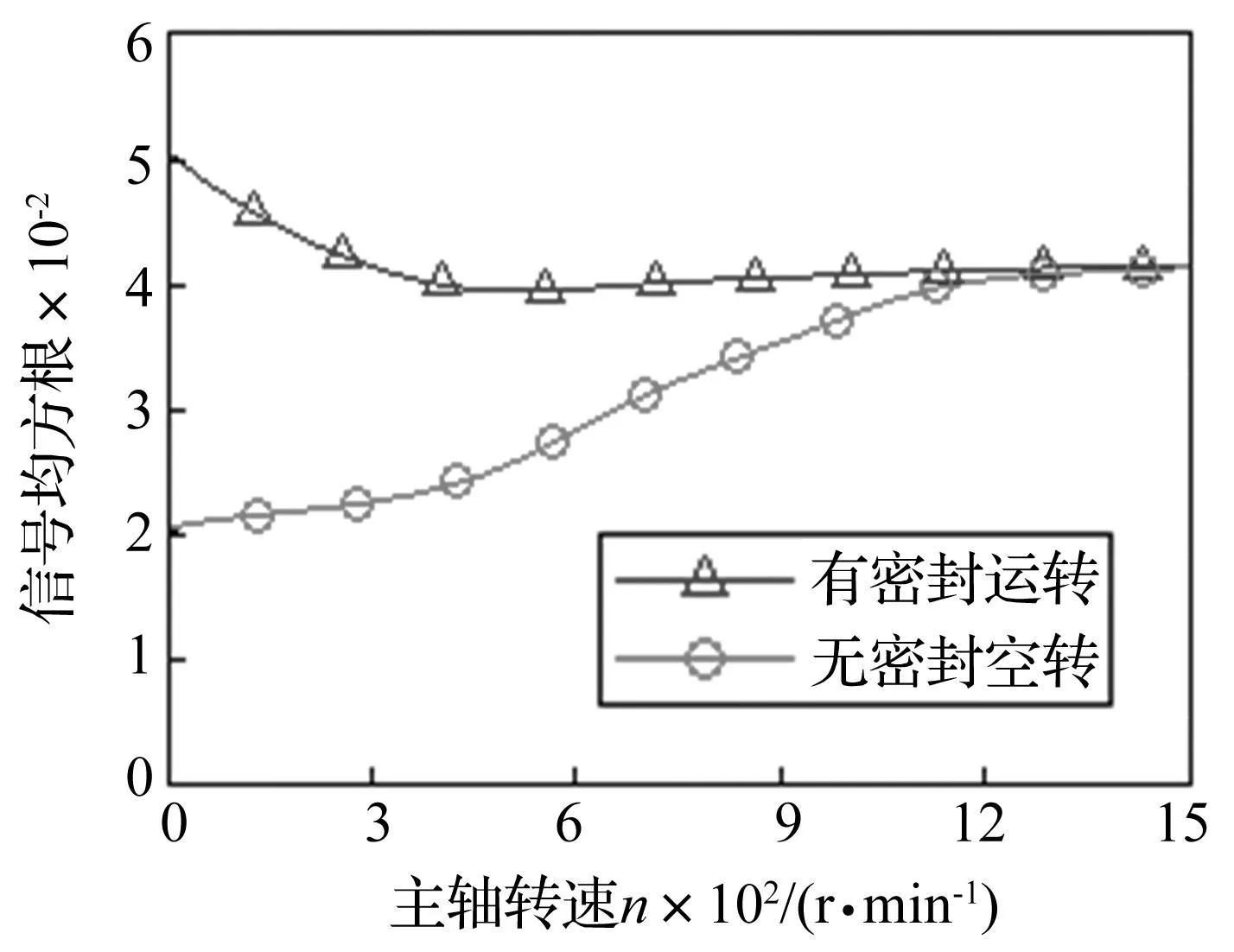
图5　声发射信号均方根Fig.5 RMS of the AE signal

图中以信号均方根来表征密封的声发射能量，并通过设备空转来估计密封声发射信号中的背景噪声。由图5知，设备空转时，声发射能量主要来自主轴，且其随着转速升高而不断增加；有密封时，声发射能量先减少后增加，最后与空转时的测量结果基本一致。造成以上结果的原因是：密封刚启动时，密封副的接触摩擦会产生强烈的声发射能量；但随后，随着密封端面开启以及液膜逐渐增厚，声发射能量迅速下降；而后，由于主轴开始对信号产生更大的影响，因此声发射能量缓慢增加；最终当转速超过1 000 r/min后，所测信号则几乎全部来自设备主轴。

3声发射信号降噪

根据机械密封的噪声特性，提出基于ANN-PF的信号降噪算法：首先利用Elman ANN建立信号的状态空间，接着利用PF对状态空间滤波降噪。

3.1ANN-PF算法原理

粒子滤波(Particle Filter, PF)是一种基于Monte Carlo思想的Bayes递推估计算法，其核心思想是通过从系统的状态空间中寻找一系列随机样本来近似系统变量的概率密度函数，并以样本均值代替积分运算，从而获得系统状态的最小方差估计。其中，从状态空间中抽取的样本则称为“粒子”[12-13]。

系统的状态空间一般可表示为：

(1)

式(1)为系统的状态方程和观测方程。其中f(·)为状态函数，h(·)为观测函数；xt是系统在t时刻的状态值，wt为对应的过程噪声；zt是系统在t时刻的观测值，vt为对应的观测噪声。

对于密封系统，由于其零部件众多，机械结构复杂，因此难以建立基于理论的状态方程。然而考虑到所测声发射信号所蕴含的时序关系，可以通过人工神经网络来对信号规律进行拟合。

人工神经网络是模拟生物神经系统进行信息处理的一种数学模型，主要通过对样本的学习和训练，从而将信息权重分配给每个神经连接。文中的信息权重即是声发射数据之间的非线性递推关系，可简记为：

xt=f(xt-1,xt-2,…xt-n)+ε

(2)

式中，n为信号的递推阶数，ε为平均误差。以下将利用Elman神经网络对f(·)求解。

Elman神经网络是一种具有局部记忆单元和反馈连接的前向神经网络，主要由输入层，隐含层，承接层，和输出层组成。其中输入层起信号传输作用，输出层起线性加权作用；隐含层的传递函数可采用线性或非线性函数；承接层用来记忆隐含层前一时刻的输出值，并返回给输入[14-15]。典型的单隐层Elman神经网络结构见图6。

图6　Elman神经网络结构Fig.6 Structure of Elman ANN

图6中输入层有n1个结点，对隐含层的连接权重为ω1；承接层有n2个结点，对隐含层的连接权重为ω2；隐含层有n2个结点，对输出层的连接权重为ω3；输出层有n3个结点。

对于随机信号序列x=[x1,x2, …,xm]，若设其满足n阶递推关系，其中n可参考AIC或FPE[16]准则定义，则训练Elman神经网络的输入样本X和输出样本Y可表示为：

(3a)

Y=[xn+1,xn+2,…,xm]T

(3b)

由式(3a)和(3b)知，Elman神经网络的输入层神经元个数为n，输出层神经元个数为1，训练样本数为m-n；另设神经网络的隐含层神经元个数为2n+1，其传递函数为tansig(·)；学习函数为learngdm(·)，训练函数为traingdx(·)，训练次数为1 000。由此得到神经网络模型fElman，从而将系统的状态空间改写为：

(4)

由于实验直接对声发射数据进行观测，因此式(4)中令观测噪声等价于过程噪声。根据式(4)对系统进行序贯重要性采样，由此对信号空间的粒子滤波过程如下：

(5)

(6)

(7)

式中,yt为t时刻下的信号观测值，p(·)为抽样空间的概率密度函数。

步骤3为防止粒子匮乏，按式(8)计算当前时刻的有效粒子数Neff：

(8)

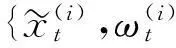
(9)

步骤4回到步骤2，对t+1时刻的粒子进行更新。

当步骤3进行重采样时，令u～U(0,1]，其中{ui:i=1, 2, …,N}独立同分布。定义函数D(·)，若：

(10)

需要说明的是，当神经网络输入层神经元数目大于2(n>2)时，其粒子权值的递推过程将比式(6)更为复杂。但本文为求简便，仍假设信号粒子在t时刻的权值ωt仅跟其当前时刻的状态xt和前一时刻权值ωt-1相关。

3.2声发射信号降噪

从每种接触状态中随机截取30个数据段，其中每个数据段包含连续采集的20 000个信号值。为了有效滤波降噪，本文首先研究信号噪声的分布特性。

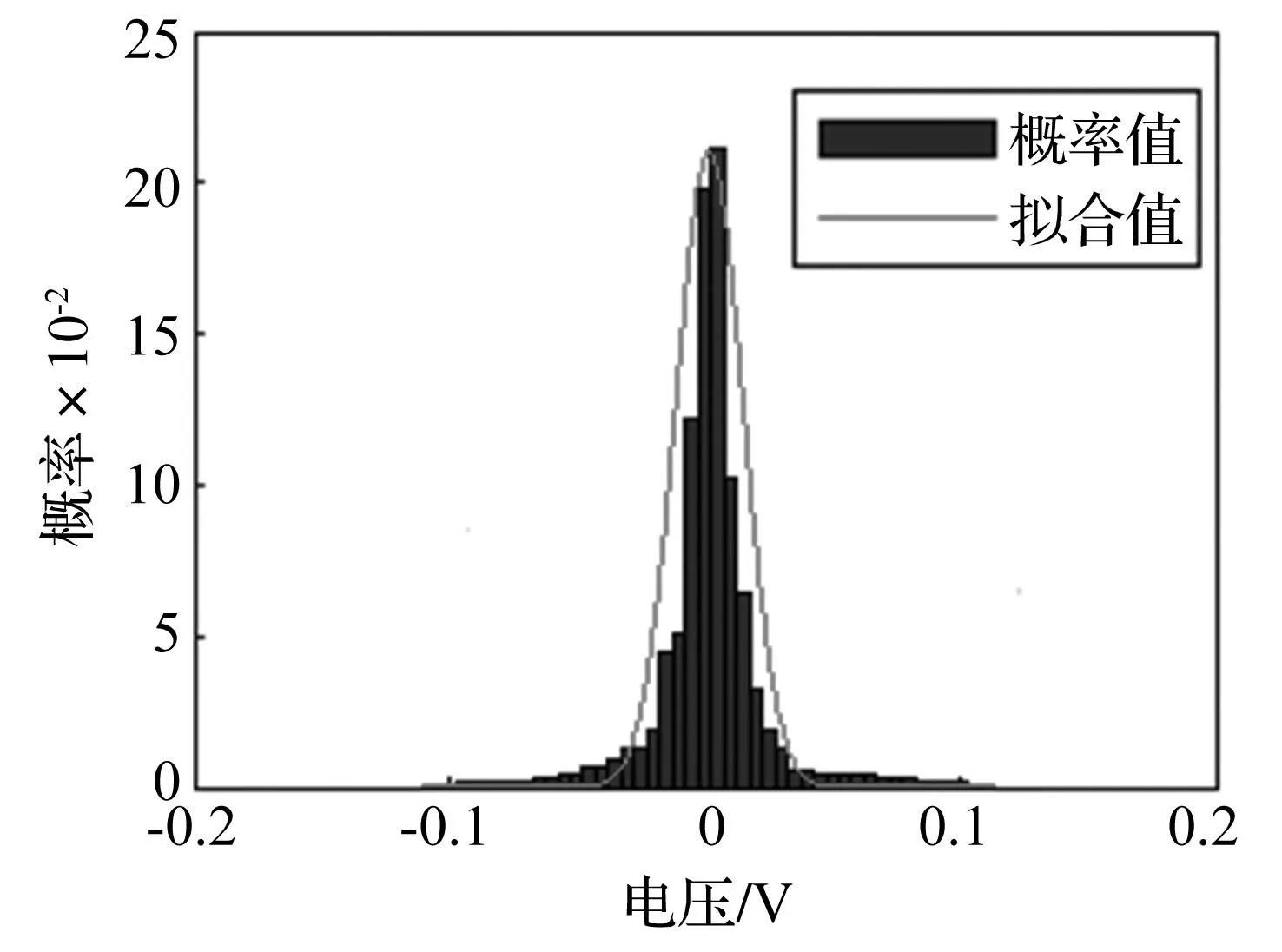
图7　噪声统计分布Fig.7 Statistic distribution of noise

图7为设备空转时的信号统计规律，由图知其服从高斯分布。若以此拟合密封的噪声空间，则实验噪声在不同转速下的分布函数见表1。

表1　噪声分布参数

根据“3.1”节步骤对密封的声发射信号进行粒子滤波，其中令p(·)选择对应转速的N(μ,σ2)以完成状态粒子的权值更新。图8和图9为滤波前后的声发射信号对比：

由图8和图9知，由于噪声干扰，未经处理的信号都存在不同程度的随机波动，这使得信号能量不够稳定，从而给密封端面的特征分析和状态识别带来困难；而ANN-PF则有效抑制了实验的背景噪声，由此使信号能量更加稳定。

图8　滤波前的声发射信号Fig.8 The AE signals without ANN-PF

图9　滤波后的声发射信号Fig.9 The AE signals processed by ANN-PF

4接触状态识别

提取多个特征来描述密封端面在不同接触状态下的声发射规律，再利用 LS-SVM来构建密封端面接触状态的识别模型。

4.1LS-SVM算法原理

SVM是建立在统计学习理论框架下的一种通用机器学习方法，其核心思想是通过某种非线性映射将原样本空间投影到高维空间，并在高维空间中寻求最优的线性划分，即最优超平面，从而解决样本空间的非线性分类问题。由于SVM采用了结构风险最小原理，因此在解决小样本、非线性及高维模式识别问题上，往往具有一定优势[17]。

LS-SVM是基于SVM的一种改进算法，它通过利用二次损失函数取代SVM中的松弛因子，将原SVM的二次寻优问题转化为解线性方程组，从而简化了计算的复杂度，提高了模型的运算速率[18-19]。

设有非线性可分的n维样本集合{xi,yi}，其中i=1～m，yi{1,-1}，yi是xi的分类标识。现有未知映射φ将样本数据映射到N(N>n)维空间，并使得新样本φ(xi)在N维空间线性可分。因此对于 LS-SVM，分类问题可表示为：

(11)

式中,ω是样本权值，b是偏置系数，ξi是损失函数，c是惩罚因子。利用Lagrange法求解上述优化问题，则有：

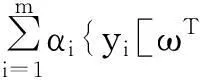
(12)

式中,αi为Lagrange乘子。根据优化条件，可得：

(13)

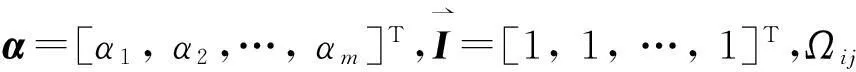
(14)

4.2端面接触状态识别

为描述密封端面在不同接触状态下的声发射特性，对每个数据段样本提取以下特征,见式(15)～式(21)

均方根(Root Mean Square, RMS):

(15)

能量方差(Energy Variance, EV)：

(16)

峰值因子(Peak to Average Ratio, PAR)：

(17)

歪度(Absolute Skewness, AS)：

(18)

歪度方差(Skewness Variance, SV)：

(19)

中心频率(Center Frequency, CF)：

(20)

频率方差(Frequency Variance, FV)：

(21)

表2　归一化特征

表2中NO.1～NO.30为端面接触状态下的样本特征，NO.31～NO.60为端面开启状态下的样本特征，NO.61～NO.90为端面分离状态下的样本特征。若将每种状态的任意10个样本特征的平均值作为统计量，则得到以下柱状图(见图10)。

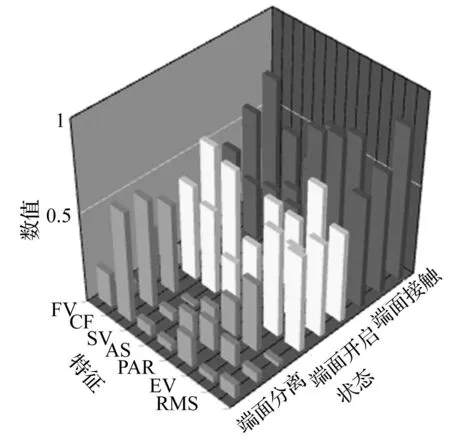
图10　特征柱状图Fig.10 Histogram of sample features

由图10可知，RMS和PAR的最大值出现在端面接触状态，而其最小值出现在端面分离状态，由此说明密封的声发射能量随其端面分开而减弱；与此同时，EV和SV的最大值出现在端面开启状态，由此说明液膜未成型时，密封的信号结构并不稳定。

利用 LS-SVM对以上特征进行识别。从每种状态中任意选择6组特征作为训练样本，而其余的作为测试样本。以径向基函数为核函数构建 LS-SVM，最终得到模型的检测率见表3。

表3　 LS-SVM识别结果

根据表3，该模型的总体检测率达到了97.2%。其中端面接触和端面分离状态下的测试样本均被正确识别；而对于端面开启状态，虽然信号结构的不稳定增加了特征的识别难度，但模型对于该状态的检测率仍超过了90%。综上可知，利用本文所提的方法来监测机械密封的端面接触状态是完全可行的。

5结论

本文主要研究了密封开启过程中的声发射特征，并建立了其端面接触状态的声发射检测模型。通过实验和数据处理，得出以下结论：

(1) 在机械密封的声发射监测中，主轴是主要的噪声源，且其在观测信号中的能量比重随着设备转速增加而升高。而当密封超过1 000 r/min后，所测信号几乎全部来自设备主轴。

(2) ANN-PF是一种基于状态空间抽样的时域降噪算法，它能够有效抑制观测信号中的随机扰动。实验中，粒子的分布函数源自对噪声空间的合理估计，因此该算法对于密封信号具有较强的灵活性和适应性。

(3) 对于所提取的特征， LS-SVM达到了理想的检测率。由此证明本文方法能有效实现密封端面接触状态的无损检测，从而为密封失效的早期预警提供良好的数据支撑。

参 考 文 献

[ 1 ] Reddyhoff T, Dwyer-Joyce R S, Harper P.A new approach for the measurement of film thickness in liquid face seals[J].Tribology Transactions, 2008, 51(2): 140-149.

[ 2 ] Astridge D G, Longfield M D.Paper 11: Capacitance measurements and oil film thickness in a large-radius disc and ring machine[J].Proceedings of the Institution of Mechanical Engineers, Conference Proceedings,SAGE Journal, 1967, 182(14): 89-96.

[ 3 ] El-Sisi S I, Shawki G S A.Measurement of oil-film thickness between disks by electrical conductivity[J].Journal of Fluids Engineering, 1960, 82(1): 12-16.

[ 4 ] Etsion I, Constantinescu I.Experimental observation of the dynamic behavior of noncontacting coned-face mechanical seals[J].ASLE Transactions, 1984, 27(3): 263-270.

[ 5 ] Anderson W B, Jarzynski J, Salant R F.A condition monitor for liquid lubricated mechanical seals[J].Tribology Transactions, 2001, 44(3): 479-483.

[ 6 ] Reddyhoff T, Dwyer-Joyce R, Harper P.Ultrasonic measurement of film thickness in mechanical seals[J].Sealing Technology, 2006, 2006(7): 7-11.

[ 7 ] Williams M, Barnes N D.The use of acoustic emissions for monitoring mechanical seals[C]//13th BPMA Pump Technical Conference,1993.

[ 8 ] Miettinen J, Siekkinen V.Acoustic emission in monitoring sliding contact behaviour[J].Wear, 1995, 181: 897-900.

[ 9 ] 高志，林尤滨，黄伟峰，等.干气密封启动过程中的声发射 信号特征[J].清华大学学报:自然科学版，2013, 53(3): 319-322.

GAO Zhi, LIN You-bin, HUANG Wei-feng, et al.Acoustic emission characteristics of dry gas seals during startup[J].Journal of Tsinghua University:Science and Technology, 2013, 53(3): 319-322.

[10] Zhang Er-qing, Fu Pan, Ge Zhen-di, et al.Mechanical seal opening condition monitoring based on acoustic emission technology[J].Sensors & Transducers,2014,172(6):139-146.

[11] 李晓晖，傅攀，张智.基于声发射技术的机械密封膜厚测量[J].四川大学学报:工程科学版，2014, 46(6): 198-204

LI Xiao-hui, FU Pan, ZHANG Zhi.Measurement of film thickness in mechanical seals based on AE technology[J].Journal of Sichuan University:Engineering Science Edition, 2014, 46(6): 198-204.

[12] Kotecha J H, Djuriê P M.Gaussian particle filtering[J].IEEE Transactions on Signal Processing, 2003, 51(10): 2592-2601.

[13] 梁军.粒子滤波算法及其应用研究[D].哈尔滨：哈尔滨工业大学，2009.

[14] 杨超，王志伟.基于Elman神经网络的滚动轴承故障诊断方法[J].轴承，2010(5): 49-52.

YANG Chao, WANG Zhi-wei.Fault diagnosis method of rolling bearings based on Elman neural network[J].Bearing, 2010(5): 49-52.

[15] 张德丰.MATLAB 神经网络应用设计[M].北京：机械工业出版社, 2009.

[16] 从飞云，陈进，董广明.基于滚动轴承故障诊断的AR预测滤波器阶数问题研究[J].振动与冲击，2012, 31(4): 44-47.

CONG Fei-yun, CHEN Jin, DONG Guang-ming.Order selection of AR predicting filter for rolling bearing diagnosis[J].Journal of Vibration and Shock, 2012, 31(4): 44-47.

[17] 王朝勇.支持向量机若干算法研究及应用[D].吉林：吉林大学，2008.

[18] 陈昌，汤宝平，吕中亮.基于威布尔分布及最小二乘支持向量机的滚动轴承退化趋势预测[J].振动与冲击，2014,33(20):52-56.

CHEN Chang, TANG Bao-ping, LÜ Zhong-liang.Degradation trend prediction of rolling bearings based on Weibull distribution and least squares support vector machine[J].Journal of Vibration and Shock, 2014, 33(20): 52-56.

[19] 郭新辰.最小二乘支持向量机算法及应用研究[D].吉林：吉林大学，2008.

The study of acoustic emission monitoring for contact state of seal end faces

LIXiao-hui1,FUPan1,CAOWei-qing1,CHENKan2(1. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. Sichuan Sunny Seal Co. Ltd., Chengdu 610041, China)

Abstract:Monitoring the contact state of seal-end faces would help to the early warning of the seal failure.For the problem of the difficulty in seal signal denoising, a new approach based on particle filtering with artificial neural network (ANN-PF) and least square support vector machine (LS-SVM) is presented for acoustic emission (AE) modeling.After measuring seal film thickness, variations of the AE energy during the seal startup are studied.Then, Elman ANN is used to build the dynamic state space (DSS) of the AE signal, and PF is used for signal filtering.Finally, multiple features are extracted and a classification model based on LS-SVM is constructed for state monitoring.Experimental data shows that the proposed method can detect the seal face contact effectively and non-destructively, and it has extensive industrial prospects.

Key words:seal face contact; acoustic emission; particle filter; state monitoring; least square support vector machine

中图分类号:TH17

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.014

通信作者傅攀 男，博士，教授，博士生导师，1961年3月生

收稿日期：2015-06-19修改稿收到日期：2015-11-04

基金项目：中央高校基本科研业务费专项资金项目(SWJTU12CX039)

第一作者 李晓晖 男，博士生，1987年8月生