水下爆炸应力波在含声学覆盖层结构中的传播规律

陈莹玉， 肖　巍， 姚熊亮， 李　烨(.哈尔滨工程大学 船舶工程学院，哈尔滨　5000; .中国海洋大学 工程学院，青岛　6600)



水下爆炸应力波在含声学覆盖层结构中的传播规律

陈莹玉1， 肖巍2， 姚熊亮1， 李烨1(1.哈尔滨工程大学 船舶工程学院，哈尔滨150001; 2.中国海洋大学 工程学院，青岛266100)

摘要：针对舰船的含声学覆盖层结构，对水下爆炸作用下应力波在该结构中的传播规律进行研究。采用二阶Godunov方法，建立水下爆炸应力波在多层介质中传播的计算模型，并与经典Taylor平板解析解进行对比验证；通过对不同工况下的应力波传播规律分析，获得边界条件、声学覆盖层厚度等参数对其影响规律，可为舰艇抗冲击设计、研究提供参考。

关键词：水下爆炸；应力波; Godunov方法; 含声学覆盖层结构

水面舰艇作为一种海上重要的作战力量不可避免地会遭受水下非接触性爆炸的攻击[1]。由于声学覆盖层同时具有隔声和抗冲击的双重功效，现今被广泛应用于舰船结构中[2]。因此，系统地对水下爆炸应力波在含声学覆盖层结构中的传播机理进行深入的研究是十分有必要的。

研究水下爆炸引起的应力波传播机理问题的方法有解析法和数值法两种。张社荣等[3]具体分析了水下爆炸冲击波传播特性。Yang等[4]基于一维波的特征线法，对入射波作用下分离式Hopkinson压杆两端应力均匀性问题进行了分析，并讨论了介质阻抗比和波形对应力均匀性的影响。Mine[5]运用经典的一维应力波理论，分析了轻型复合装甲在弹片冲击下的力学特性，并得到了层间材料、层厚和冲击速度等参数对复合装甲相应的影响。基于Floquet 理论，Chen等[6]针对均质层状的平板结构的冲击问题提出了一种解析法。Lin等[7-8]基于拉普拉斯变换对多层介质的动响应进行了研究。Jin等[9]提出了一种计算水下爆炸载荷作用下多层介质各个界面上的压力的解析法，该方法的结果和有限元分析结果十分吻合，但该方法只能给出界面处的应力状态。

随着问题的复杂边界科学技术的发展，对应力波进行数值解的需求也越来越强烈。Tasdemirci等[10]利用试验和数值的方法，研究了多层材料在高应变率下的力学行为和应力波作用下的塑性变形效应。Desceliere等[11]采用混合数值解法模拟了在脉冲载荷作用下多层半无限介质的应力波传播过程。Brasek[12-13]模拟了阶跃载荷作用下一维含涂覆层的铝结构，并给出了指数衰减冲击波作用下的有限元解。Tang等[14]建立了一种计算流体弹塑性介质中波动的二阶Godunov方法。Gong等[15]采用耦合有限元和DAA边界的程序对水下爆炸冲击波的动响应进行了模拟，但该研究注重于流固耦合面处压力的求解。

应力波在杆、板等简单结构中的传播特性研究较深入，但对于含覆盖层结构的传播特性这方面的研究较少；另外从载荷方面来看针对的大多数是轴向矩形脉冲载荷，研究主要集中在地震和工程爆破中，在水下爆炸领域的研究较少。为此，本文在已有研究基础上，基于二阶Godunov方法，建立水下爆炸应力波在多层介质中传播的计算方法，并对各种工况下爆炸应力波在介质中的传播规律进行总结。

1计算模型及方法

1.1控制方程

拉格朗日坐标中一维弹塑性介质的控制方程为守恒方程组[15]：

(1)

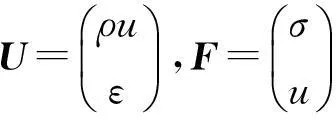
上述方程中t为时间，x为拉格朗日坐标，而ρ，u，ε，σ分别为密度，速度，应变，应力。

弹塑性介质的本构关系可以表示为[14]:

(2)

式中，κ为屈服应力，E为弹性阶段的杨氏模量，Ep为塑性阶段的杨氏模量。

1.2Riemann问题

为了避免计算ε，采用Godunov法对计算过程进行了优化。对于简单波，可以得到以下相容关系[16]：

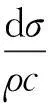
(3)

式中，∓分别对应右行波和左行波。弹性范围内c=c0，塑性范围c=c(κ)。

考虑守恒方程式(1)与如下初始条件组成了Riemann问题：

(4)

(5)

消去式(5)中的u*，得到

(6)

采用牛顿迭代法：

(7)

(8)

根据式(7)、(8)，可以得到σ*，将其代入式(5)即可得到u*。以上得到的σ*，u*，即Godunov方法的第一步。

1.3差分格式

考虑网格单元[tn,tn+1]×[xi,xi+1]。将式(1)在此单元上积分，有：

(9)

式中，Δt=tn+1-tn，Δx=xi+1-xi。为了保证数值的稳定性，CFL数条件满足：c0Δt/Δx≤1。

(10)

以上即为Godunov方法的第二步。

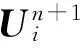
2有效性验证

Taylor[17]提出了水下爆炸作用下简单平板的动响应的解析解。对于入射波为P0e-t/θ，平板结构的速度和压力响应可以表示为：

(11)

(12)

式中，m=h0ρp；h0，ρp分别为平板的厚度和密度。βa=ρwcwθ/m，为流固耦合参数。ρw，cw分别为水的密度和声速。P0为入射冲击波的压力峰值。

本节采用经典的Taylor 平板理论验证本文的Godunov 法解决水下爆炸应力波问题的有效性。计算工况为，平板的厚度取为20 mm，入射波的峰值取为1 MPa，时间衰减常数取为6×10-4s。计算模型的材料参数如表1所示。

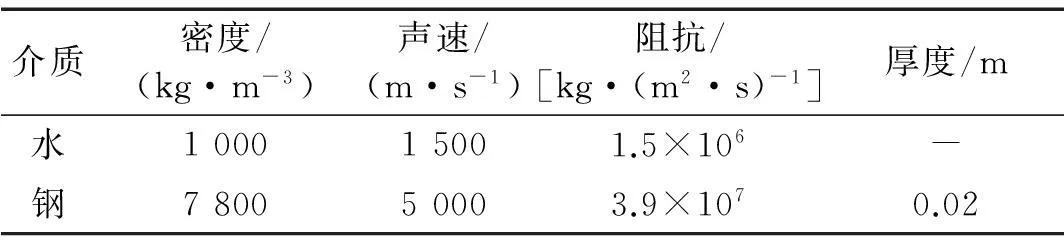
表1　材料参数

图1和图2分别为流固耦合处的无量纲压力、无量纲速度的时历曲线。时间的无量纲因子为时间衰减常数θ，而压力和速度的无量纲因子分别为P0和P0/ρwcw。图中实线为数值解，点线为解析解。从图1中可以看到，本文Godunov 法计算得到的压力曲线，在峰值与变化趋势方面，均与经典的Taylor平板理论符合较好。应力波在结构中传播时，在不同界面处产生的入射、反射和透射将会引起的压力变化。Godunov法计及了在界面处的压力变化，得到了更为准确的峰值1.927。图2中，速度的数值解和解析解在峰值和变化趋势同样吻合良好。因此，本文的Godunov方法更准确和清晰地给出了水下爆炸作用下钢板的动响应。

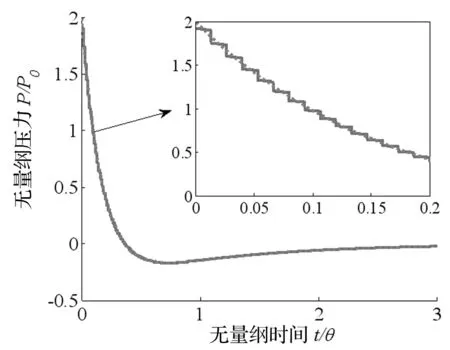
图1　流固耦合处的压力时历曲线(实线为数值解，点线为解析解)Fig.1 The pressure on FSI boundary(Solid line: the numerical solution; Dotted line: the analytical solution)

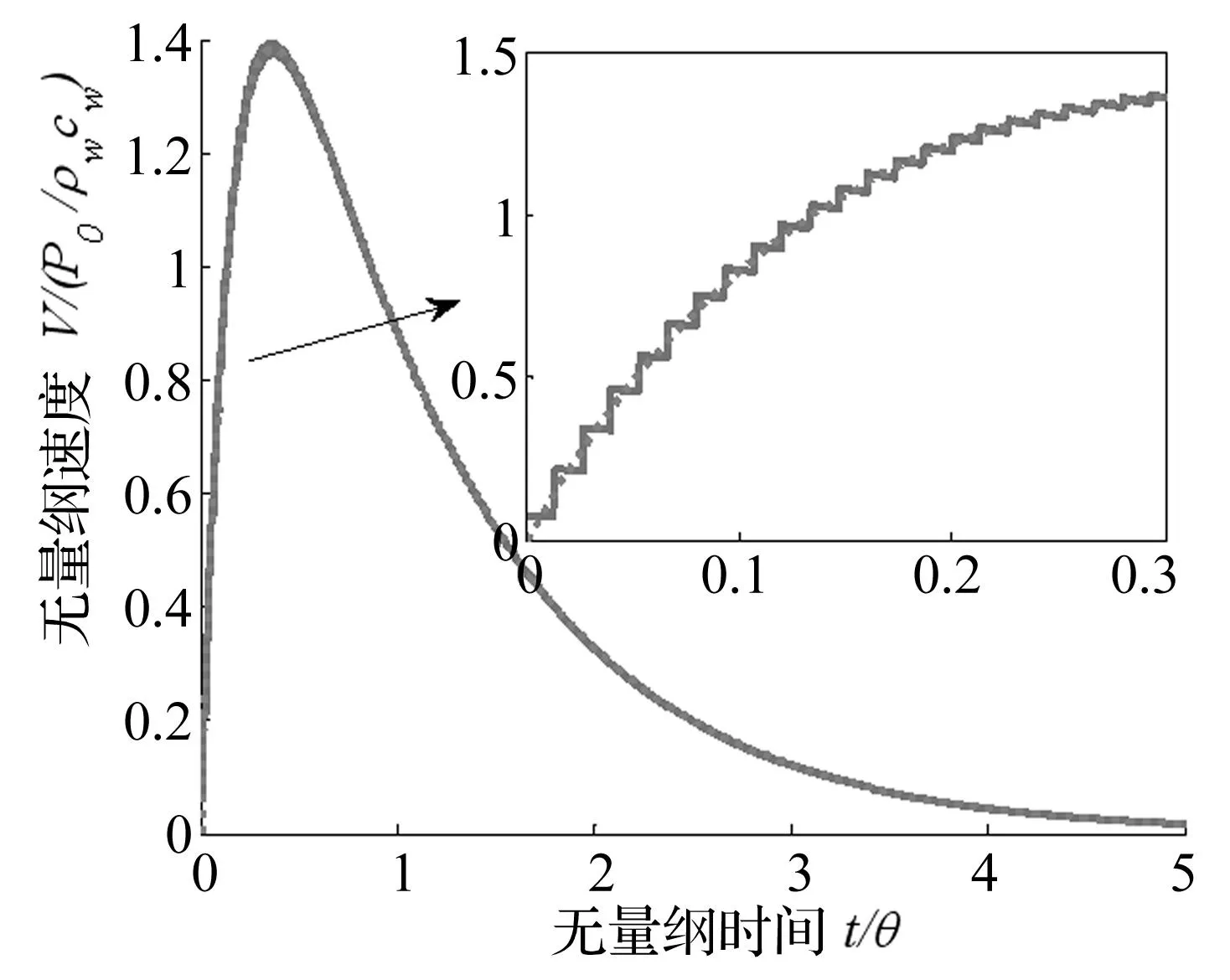
图2　流固耦合处的速度时历曲线(实线为数值解，点线为解析解)Fig.2 The velocity on FSI boundary(Solid line: the numerical solution; Dotted line: the analytical solution)

3结果与分析

随着声学覆盖层在舰船上的广泛使用，深入地对水下爆炸应力波在多层介质结构中的传播规律是十分有必要的。本文选取水下爆炸工程实际问题中常遇到的两个典型结构模型进行数值计算分析，如图1所示。一是含声学覆盖层的背空钢板，即边界Ⅲ的右侧的介质为空气；二是含声学覆盖层的背水钢板，即边界Ⅲ的右侧的介质为水。

图3　计算模型示意图Fig.3 Calculation model

水下爆炸冲击过程十分复杂。然而，为深入理解应力波在多层介质中传播的基本物理过程，本文将应力波在水-声学覆盖层-钢-水/空气系统中的传播问题视为弱冲击波在多层介质中传播的一维问题。并提出以下假设：① 各层介质为均质材料；② 应力波在介质中以纵波的形式传播。表2中给出了计算模型中的材料参数。

表2　材料参数

3.1边界条件的影响

3.1.1含声学覆盖层的背空钢板

首先计算和分析水下爆炸应力波在含声学覆盖层的背空钢板中的传播过程。计算中，声学覆盖层的厚度为50 mm，钢板厚度为20 mm，具体材料参数见表2。入射波的峰值取为1 MPa，时间衰减常数取为6×10-4s。四个不同时刻的应力分布如图4所示。图中，x<0 cm表示水域，x=0 cm表示水-声学覆盖层耦合面(边界Ⅰ)，x=5 cm表示声学覆盖层-钢板耦合面(边界Ⅱ)，x=7 cm表示钢板自由面(边界Ⅲ)。为了清晰地捕捉和描述应力波在不同介质的分界面上的传播规律，选取以下四个典型的时刻进行分析：

(1)t=t0，即应力波刚传播至边界Ⅰ。由于在界面Ⅰ处发生了反射和透射，明显看到界面处的压力峰值骤升至1.12 MPa，而界面两端的压力还保持原来的状态。

(2)t=t1，应力波刚传播至边界Ⅱ。经过边界Ⅰ后，应力波波幅在声学覆盖层内保持不变；而在界面Ⅱ处的反射和透射使得压力峰值由原来的1.12 MPa骤升至2.13 MPa。

(3)t=t2，应力波刚传播至边界Ⅲ。由于边界Ⅲ为背空条件，该界面的压力直接卸载至0 MPa；而该时刻下声学覆盖层和钢板的应力分布是应力波叠加的结果。

(4)t=t3，应力波传播在结构中传播了一次的时间，即重新传播至边界Ⅰ。界面处的相互作用使得应力峰值变为1.9 MPa。

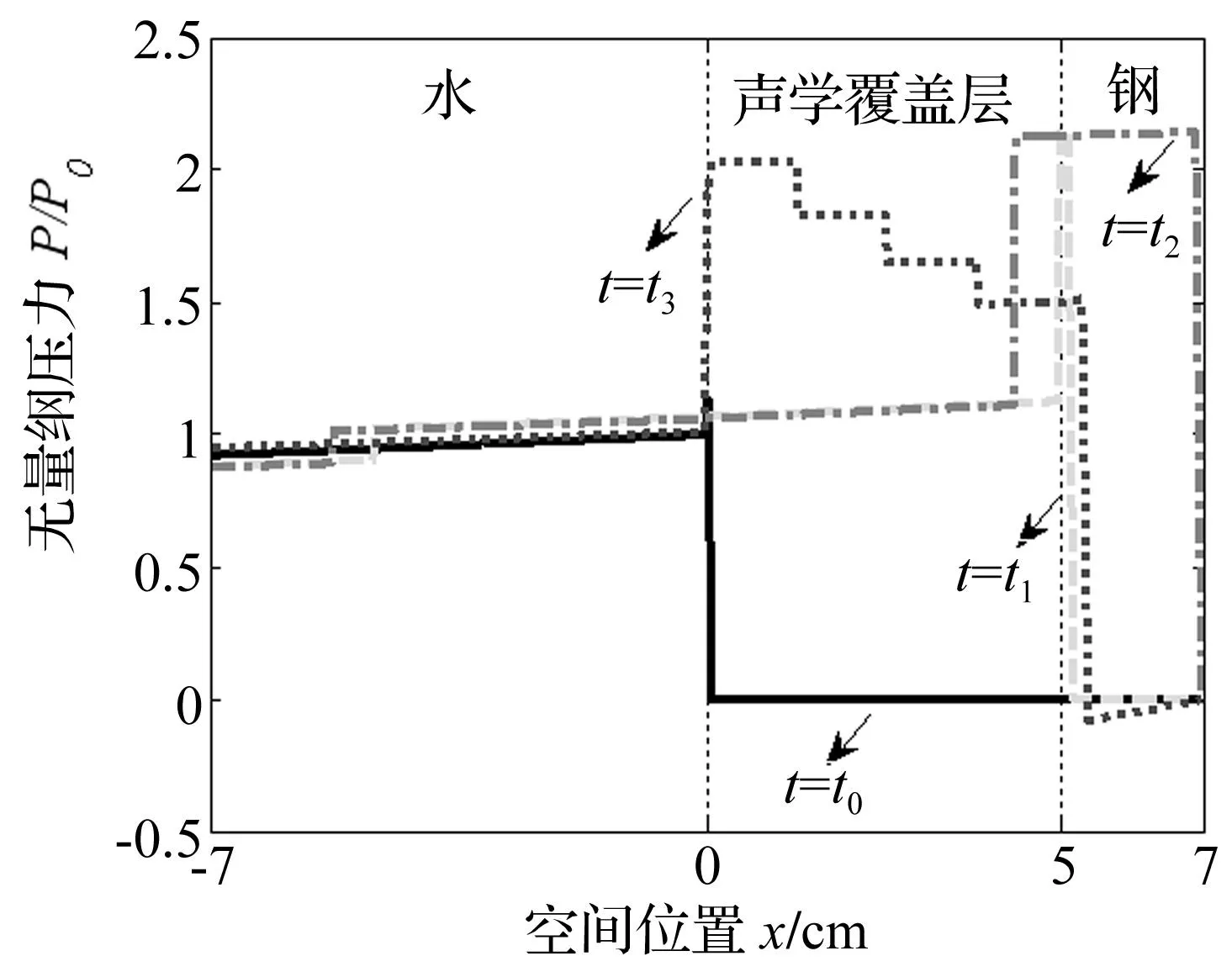
图4　背空条件下不同时刻的应力分布 (实线t=t0；虚线：t=t1；点划线：t=t2；点线：t=t3；)Fig.4 Stress distribution on different moment for air-backed condition(Solid line: t=t0; Dashed line: t=t1; Dot-dashed line: t=t2; Dotted line: t=t3)

图5　不同分界面处的应力时历曲线(实线为边界Ⅰ，点线为边界Ⅱ)Fig 5.The pressure on different boundary(Solid line: boundary Ⅰ; Dotted line: boundary Ⅱ)

在图4的基础上，图5给出了各个分界面处的无量纲应力时历曲线。从曲线的总体趋势来看，边界Ⅰ在受到冲击波作用后，压力在很短时间内从0值骤升至首个峰值，该峰值过后又很快跃升至另一个峰值，随后迅速衰减到负值。经过时间t1，应力波才传播至边界Ⅱ，边界Ⅱ上的压力从0骤升至峰值，随后迅速衰减至负值。由图5可知，边界Ⅰ上的应力峰值明显小于边界Ⅱ。边界Ⅰ、边界Ⅱ上的应力峰值分别是入射波峰值的1.90倍和2.13倍。和简单背空平板结构不同，含声学覆盖层的结构的流固耦合面的压力(边界Ⅰ)的初值仅为入射波峰值的1.12倍，这表明声学覆盖层能有效地吸收能量。

图6为边界Ⅰ和边界Ⅱ上的无量纲速度时历曲线。速度时历曲线与压力变化曲线密切相关。边界Ⅰ在受到冲击波作用后，速度从0跃升至首个峰值，随后迅速降至负值；随着该界面上压力的增加，速度达到峰值。随着压力作用在边界Ⅱ上，该边界处速度逐渐升至峰值。边界Ⅰ和边界Ⅱ的速度在前期速度略有差异，边界Ⅱ的速度峰值略大；随着时间的增加，在后期两者的速度趋于一致。

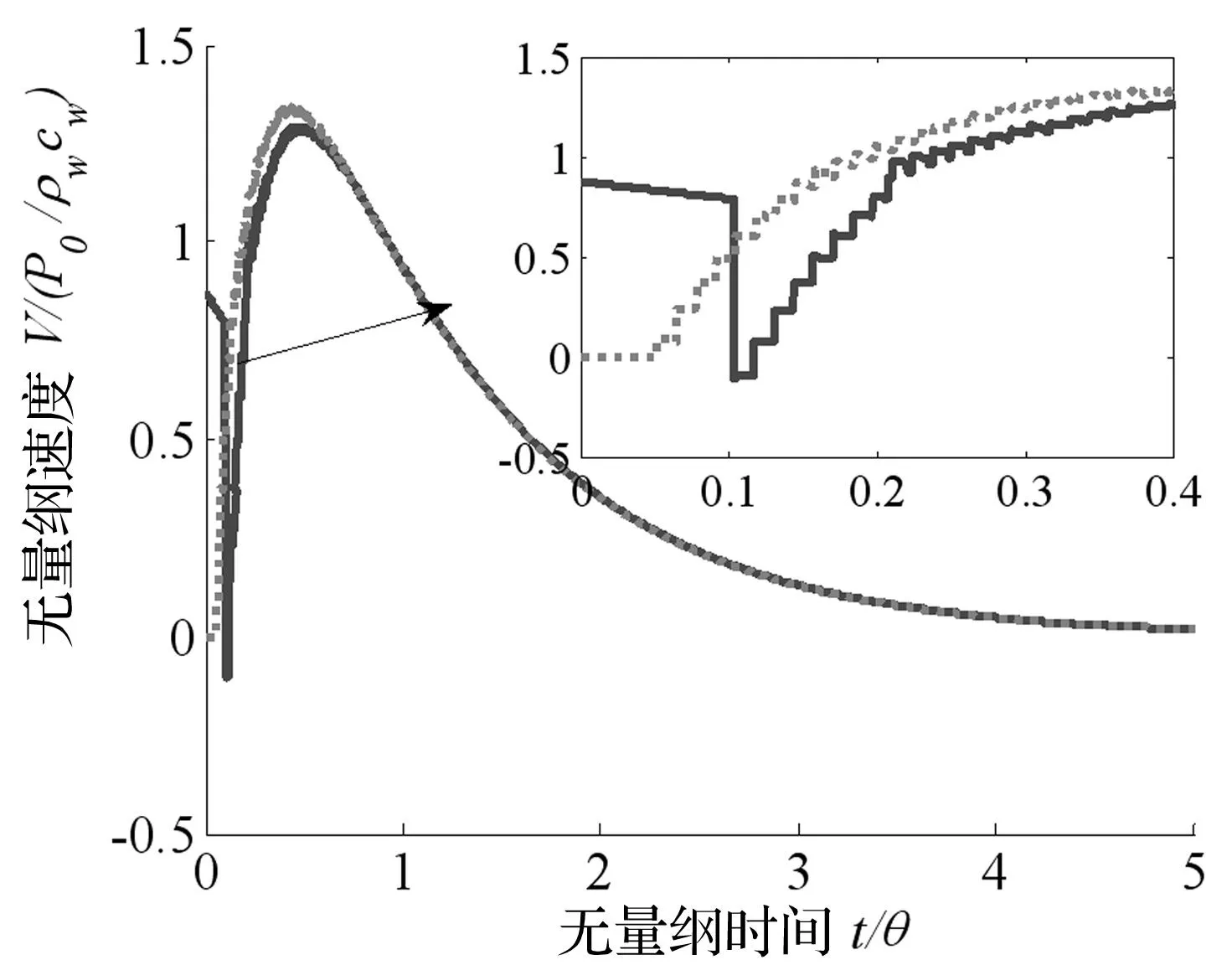
图6　不同分界面处的速度时历曲线(实线为边界Ⅰ，点线为边界Ⅱ)Fig 6.The velocity on different boundary(Solid line: boundary Ⅰ; Dotted line: boundary Ⅱ)

3.1.2含声学覆盖层的背水钢板

背水条件下的含声学覆盖层结构在舰船的舷侧防护结构中非常重要的一种结构形式。根据3.1.1节讨论的思路，本节对相同工况下含声学覆盖层的背水钢板的响应进行讨论。

图7对应地描述了四个不同时刻的应力分布。图中，x<0表示水域，x=0 cm表示水-声学覆盖层耦合面(边界Ⅰ)，x=5 cm表示声学覆盖层-钢板耦合面(边界Ⅱ)，x=7 cm表示钢板自由面(边界Ⅲ)。由图4和图7对比可知，在应力波到达边界Ⅲ之前，结构的应力状态是一致的。当应力波到达边界Ⅲ时(t=t2)，由于边界条件的改变，背水条件下边界Ⅲ的应力不再为0。同样可以看到图7中t=t3时刻的应力在钢板中应力状态，该介质中的应力为某个正值。

图8为各个分界面处的无量纲应力时历曲线。图中边界Ⅰ、边界Ⅱ、边界Ⅲ上的应力峰值分别是入射波峰值的1.90倍、2.13倍和0.77倍。应力的早期响应和背空条件下的响应一致，且边界Ⅰ和边界Ⅱ上的应力峰值保持一致；后期由于边界条件的影响，一部分的应力波透射入边界Ⅲ后面的水中，引起了边界Ⅲ上的应力变化。而应力的叠加使得背水条件下各边界面上的压力均为正值。

图7　不同时刻的应力分布 (实线：t=t0；虚线：t= t1；点划线：t=t2；点线：t=t3；)Fig.7 Stress distribution on different moment for water-backed condition(Solid line: t=t0; Dashed line: t=t1; Dot-dashed line: t=t2; Dotted line: t=t3)

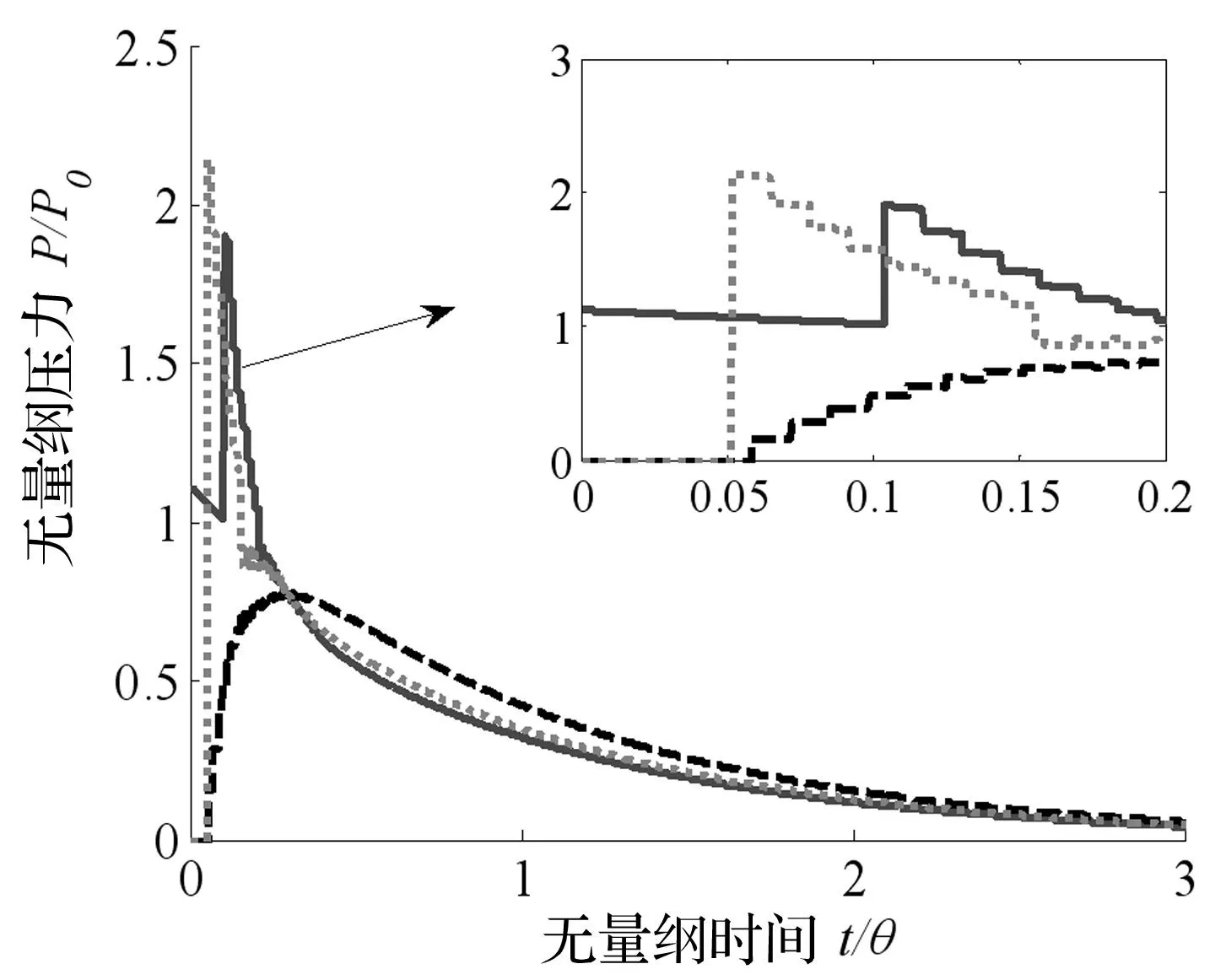
图8　不同介质的分界面处的应力分布(实线为边界I，点线为边界Ⅱ，虚线为边界Ⅲ)Fig.8 The pressure on different boundary(Solid line: boundary Ⅰ; Dotted line: boundary Ⅱ; Dashed line: boundary Ⅲ)

图9　不同介质的分界面处的速度分布(实线为边界Ⅰ，点线为边界Ⅱ，虚线为边界Ⅲ)Fig.9 The pressure on different boundary(Solid line: boundary Ⅰ; Dotted line: boundary Ⅱ; Dashed line: boundary Ⅲ)

各个分界面的无量纲速度时历曲线由图9给出。由于钢板中的波速是声学覆盖层的3倍，钢板厚度相对较薄，因此边界Ⅱ和边界Ⅲ的速度变化趋势几乎一致。而由于材料的差异，边界Ⅰ和边界Ⅱ的速度在前期略有差异。

对比图5～图8可知，水下爆炸应力波在背空和背水边界条件下的传播特性存在较大的差异。背空条件下，边界Ⅰ、Ⅱ上的压力迅速升至峰值后迅速衰减至负值；而在背水条件下，由于一部分波透射入背后的水中，边界上的压力不会产生负值。背空条件下声学覆盖层的速度峰值、冲击波冲量均比背水条件大很多，对结构的潜在破坏能力较强。

3.2声学覆盖层厚度的影响

为了讨论声学覆盖层厚度对抗爆抗冲击的影响，本节以背水板为例，取无量纲参数：hF/hB。其中，hF、hB分别为声学覆盖层和钢板的厚度。本节钢板的厚度hB统一取为0.02 m，而hF/hB分别取1、2、3、4和5。入射冲击波同样取为：P0e-t/θ，P0=1 MPa，θ=6×10-4。分界面上压力值的无量纲因子取为P0，时间的无量纲因子为θ。对于爆炸冲量，无量纲因子取为P0θ。图10给出了hF/hB分别取1～5时，边界Ⅰ和边界Ⅱ对应的压力时历曲线。由图10(a)可知，随着hF/hB的增加，边界Ⅰ延缓了峰值跃至峰值的时间，并有效的减小了脉宽；在边界Ⅱ也可以得到类似结论，hF/hB的增加可以有效减小脉宽。

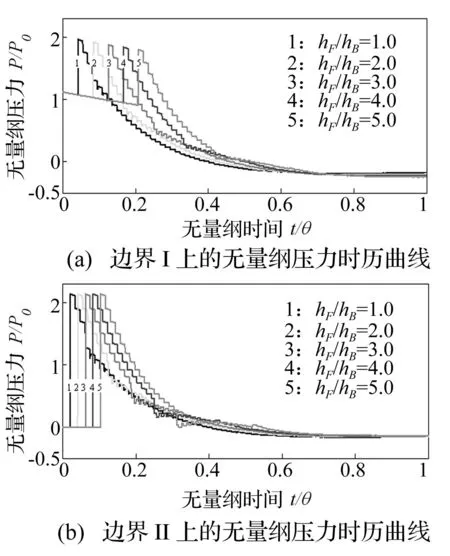
图10　无量纲压力时历曲线Fig.10 Time history response of normalised pressure

图11给出了hF/hB分别取1～5时，边界Ⅰ和边界 Ⅱ对应的爆炸冲量时历曲线。由图11可知，随着hF/hB的增加，作用在边界Ⅰ上的冲量明显增加，而作用在边界Ⅱ上的冲量明显减小，表明增加声学覆盖层的厚度能有效地吸收爆炸冲量，进而实现对舰船结构的防护。从图11仍可以看到，边界Ⅱ上冲量的减小量并不可观，即增加声学覆盖层的厚度对抗冲击性能的提高有改善但并不显著。

结合图10和图11，图12给出了边界Ⅰ和边界Ⅱ上的压力峰值以及冲量峰值随hF/hB的变化曲线。对于边界Ⅰ，随着hF/hB的增加压力峰值减小，而冲量峰值显著增加；对于边界Ⅱ，随着hF/hB的增加压力峰值和冲量峰值也在显著地减小。这表明，增加声学覆盖层的厚度能够减小流固耦合面处的峰值压力并吸收更多的爆炸冲量，进一步减小钢结构的冲量，对钢结构有保护作用。

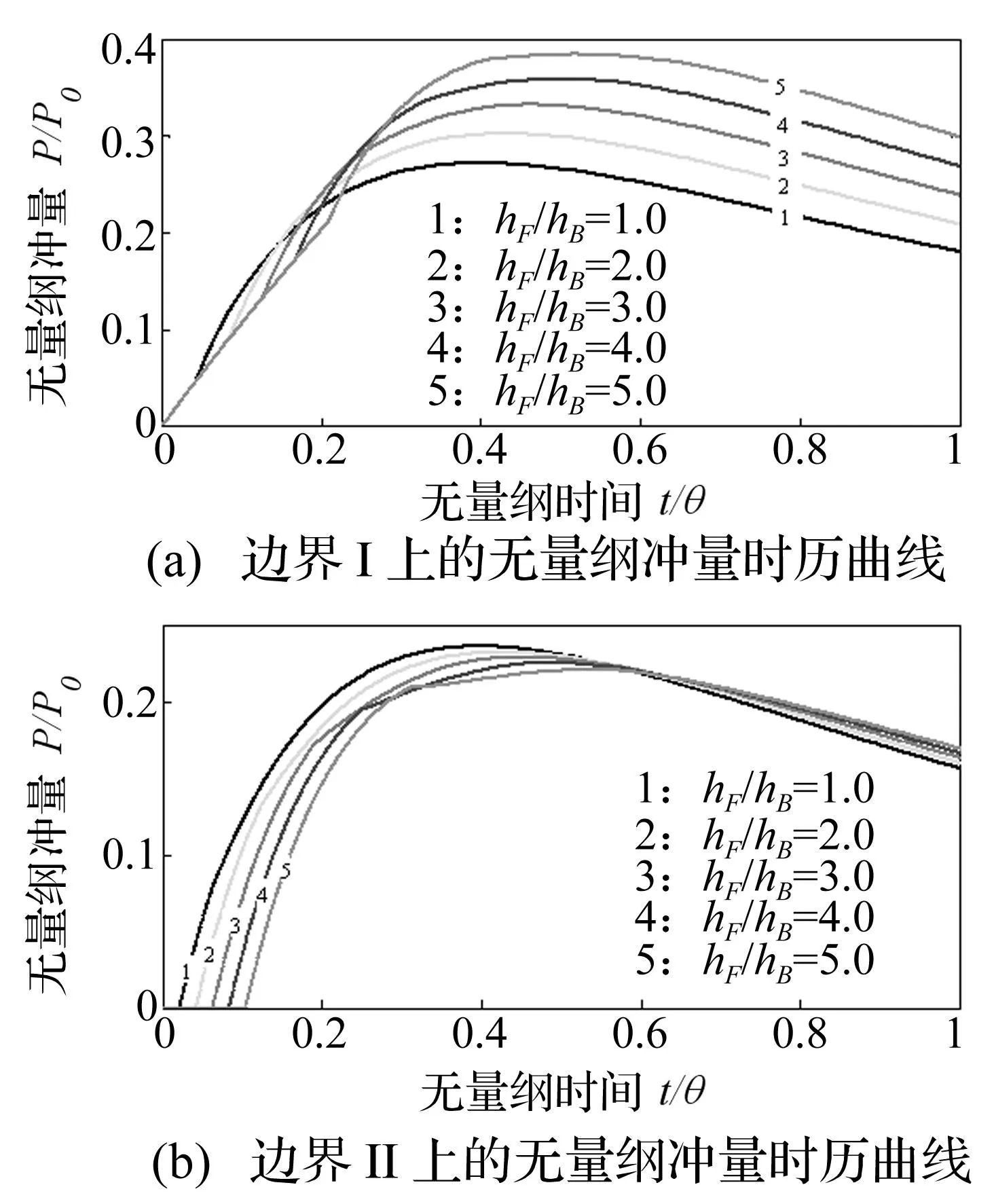
图11　无量纲冲量时历曲线Fig.11 Time history response of normalised impulse

图12　压力以及冲量峰值随hF/hB的变化曲线Fig.12 The peak value of pressure and impulse on boundary Ⅰ and boundary Ⅱ chaged with hF/hB

4结论

基于二阶Godunov方法，本文建立了水下爆炸应力波在含声学覆盖层结构中传播的计算模型，对不同工况下的应力波的传播规律进行了分析，获得边界条件、声学覆盖层厚度等工参数对抗冲击性能影响规律，得到以下结论：

(1) 与简单背空平板结构不同，含声学覆盖层的结构的流固耦合面的压力的初值仅为入射波峰值的1.12倍，这表明声学覆盖层能有效地吸收能量。

(2) 应力波在背水和背空边界条件下的传播特性存在较大的差异。背空条件下，边界上的压力迅速升至峰值后迅速衰减至负值；而在背水条件下，由于一部分波透射入背后的水中，边界上的压力不会产生负值。背空条件下声学覆盖层的速度峰值、冲击波冲量均比背水条件大很多，对结构的潜在破坏能力较强。

(3) 声学覆盖层厚度对冲击波传播特性存在较大的影响。增加声学覆盖层的厚度，能延缓各个边界面上压力峰值跃至峰值的时间、有效的减小了脉宽，并有效地吸收爆炸冲量，进而实现对舰船结构的防护。

参 考 文 献

[ 1 ] Zhang A Man, Yang Wen-shan, Yao Xiong-liang.Numerical simulation of underwater contact explosion [J].Applied Ocean Research, 2012, 34:10-20.

[ 2 ] Chen Yong, Wang Yu, Hua Hong-xing.An analytic model for the water blast response of one-dimensional marine structure coated with elastic foam [J].Archive of Applied Mechanics, 2010, 80: 1243-1253.

[ 3 ] 张社荣,孔源,王高辉.水下和空中爆炸冲击波传播特性对比分析[J].振动与冲击,2014,33(13):148-153.

ZHANG She-rong, KONG Yuan, WANG Gao-hui.Comparative analysis on propagation characteristics of shock wave induced by underwater and air explosions[J].Journal of Vibration and Shock,2014,33(13):148-153.

[ 4 ] Yang L M, Shim V P W.An analysis of stress uniformity in split Hopkinson bar test specimens [J].International Journal of Impact Engineering, 2005, 31:129-150.

[ 5 ] Mines R A W.A one-dimensional stress wave analysis of a lightweight composite armour [J].Composite Structures,2004,64(1):55-62.

[ 6 ] Chen X, Chandra N, Rajendran A M.Analytical solution to the plate impact problem of layered heterogeneous material systems [J].International Journal of Solids and Structures, 2004, 41: 4635-4659.

[ 7 ] Lin Y H, Ma C C.Transient analysis of elastic wave propagation in multilayered structures [J].CMC, 2011, 24: 15-42.

[ 8 ] Lin Y H, Ma C C.The investigation of effective material concept for the transient wave propagation in multilayered media [J].Journal of Mechanics, 2012, 28: 247-260.

[ 9 ] Jin Z, Yin C, Chen Y, et al.An analytical method for the response of coated plates subjected to one-dimensional underwater weak shock wave [J].Shock and Vibration, 2014,2014:803751.

[10] Tasdemirci A, Hall I W.The effects of plastic deformation on stress wave propagation in multi-layer materials[J].International Journal of Impact Engineering,2007,34:1797-1813.

[11] Desceliers C, Soize C, Grimal Q,et al.A time-domain method to solve transient elastic wave propagation in a multilayer medium with a hybrid spectral-finite element space approximation [J].Wave Motion, 2008,45:383-399.

[12] Brasek T P.Effect of surface coating on one-dimensional system subjected to unit step pressure wave [D].California: Naval postgraduate School, NPS-ME-94-006, 1994.

[13] Brasek T P.Response of dual-layered structures subjected to shock pressure wave [D].California: Naval Postgraduate School, 1994.

[14] Tang H S, Sotiropoulos F. A second-order Godunov method for wave problems in coupled solid-water-gas systems [J].Journal of Computational Physics, 1999,151(2): 790-815.

[15] Gong S W,Lam K Y.Analysis of layered composite beam to underwater shock including structural damping and stiffness effects[J].Shock and Vibration,2002,9(6): 283-291.

[16] Lin Xiao.Numerical computation of stress waves in solid[M].Berlin:Akademie Verlag Gmbh, 1996:14-24.

[17] Taylor G I.The pressure and impulse of submarine explosion waves on plates.[M]//Underwater Explosion Research,Vol.I: Arlington,VA: Office of Naval Research, 1950:1155-1173.

Wave propagation mechanism in coating plates subjected to underwater explosion

CHENYing-yu1,XIAOWei2,YAOXiong-liang1,LIYe1(1.College of Shipbuilding Engineering, Harbin Engineering University, Harbin 230031, China;2.College of Engineering, Ocean University of China, Qingdao 266100, China)

Abstract:Coated plates are widely used in naval ship structures for better protection from underwater explosion.Understanding the wave-propagation mechanism in multilayered mediums is very important.A second-order Godunov method was used to establish the calculation model for the wave-propagation mechanism in coating plates subjected to underwater explosion.The numerical results are in good agreement with Taylor’s solution.Different boundary conditions and thinness of the coated plate were considered to obtain their effects on the coated plates.The results offered a reference for designing and studying submarines’s shock resistance．

Key words:underwater explosion; stress waves; Godunov method; coating plate

中图分类号:O347.4+4

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.002

通信作者姚熊亮 男，博士,教授,1963年2月生

收稿日期：2015-02-10修改稿收到日期：2015-04-24

基金项目：国家自然科学基金项目(U1430236;51479041;51279038)

第一作者 陈莹玉 女，博士生，1991年11月生

E-mail： yaoxionglianghrbeu@163.com