空间太阳能电站的轨道、姿态和结构振动的耦合动力学建模及辛求解*

魏乙 邓子辰李庆军 文奋强

（西北工业大学工程力学系，西安 710072）

空间太阳能电站的轨道、姿态和结构振动的耦合动力学建模及辛求解*

魏乙 邓子辰†李庆军 文奋强

（西北工业大学工程力学系，西安 710072）

作为一种从太空获得清洁能源的系统，空间太阳能电站（SPS）吸引着许多国家和科研机构的关注.由于其超大、超轻的柔性结构特点，研究其在轨动力学行为时需要考虑轨道、姿态和结构振动的耦合作用.本文在考虑地球的非球形摄动影响下，建立了集成对称聚光系统（ISC）的动力学模型.通过Legendre变换引入广义动量，在Hamilton体系下建立了其轨道、姿态、轴向振动耦合的动力学方程.采用辛Runge-Kutta方法对耦合动力学方程进行数值求解.根据数值结果，分别研究了其在地球同步轨道下二阶摄动项对轨道、姿态和结构振动的影响，并分析了总能量的变化情况.

空间太阳能电站， 轨道， 姿态， 结构振动， 辛

引言

随着全球经济的不断发展，能源与环境问题已成为当今最引人注目的两大课题.自从1968年美国人Glaser首次提出建立空间太阳能电站（SPS）的设想以来，SPS吸引着许多国家和科研机构的关注.美、日、欧等相继提出了20多种概念，并开展了一系列探索性的研究工作［1-6］.但是这些工作基本上都是针对不同结构形式SPS建造和运行的可行性论证，对于这类超大型航天器在轨正常运行所需要研究和解决的轨道、姿态以及结构的强非线性耦合动力学问题，还缺乏针对性的、深入的研究.

在研究小型航天器的轨道运动、姿态变化、结构振动时，由于它们之间的相互影响很小，为了计算和讨论的方便，往往把它们看作是独立的运动，分别进行分析讨论［7］.然而，对于像SPS这样的超大的柔性航天器，必须考虑轨道、姿态、以及结构振动之间的耦合作用.Wie等［8］在考虑地球非球形摄动以及太阳光压的影响下，研究了平板式SPS系统轨道和姿态的耦合动力学及控制.McNally等［9，10］研究了平板式SPS系统在同步的Laplace平面轨道和地球同步轨道的轨道动力学和姿态动力学，并分别进行了比较.然而，以上的工作都是把SPS看作是刚体，并没有考虑系统的柔性.Malla等［11］将超大空间柔性结构抽象成哑铃模型，研究了轨道离心率的变化对其姿态角和轴向变形的影响；随后，针对低空地球轨道和同步地球轨道平面运动的超大空间柔性结构，Malla［12］研究了初始条件对轴向变形、姿态角和轨道高度的影响.Ishimura等［13］使用有限元建模，通过Lagrange方法建立了分布式绳系SPS结构变形和姿态运动的动力学方程，研究了太阳能电池板及绳的变形和姿态运动的耦合问题；随后，Ishimura等［14］又把绳系SPS系统抽象成轴向可以伸缩的哑铃模型，通过将微分方程线性化，研究了轨道运动、俯仰运动、轴向振动之间的耦合现象.然而，对于超大柔性SPS的轨道、姿态、弹性振动三者结合在一起的动力学研究还很少.

对于轨道、姿态和结构振动得到的耦合动力学方程，很难用分析方法进行求解，只能用数值方法进行求解.对于数值求解方法，冯康先生［15］认为：“问题原型的基本特征在离散后应该尽可能的得到保持，而为了达到这一效果则离散化应尽可能在问题原型的同一形式框架中进行.”然而传统的数值方法，如非辛Runge-Kutta方法，Newmark方法，广义α方法等，会产生人为的数值耗散，并且会破坏系统本身具有的特征，如辛性、能量、动量等.所以国内外有许多的数学和力学的专家学者从事保结构算法的研究［16-19］.正是由于保结构算法可以保持上述的某些性质，已经有很多学者将该算法应用到航天领域.赵长印等［20］用辛算法和非辛Runge-Kutta方法计算了轴对称星系模型中恒星的运动，经过比较，证明了辛算法有高效、系统的能量误差没有长期积累、相空间几何结构不因长时间计算而受歪曲等不可比拟的优点.

对于保守体系的动力学问题，选择Hamilton体系近年来已经被学术界广泛认同.本文通过Legendre变换引入广义动量，在Hamilton体系下建立了集成对称聚光系统（ISC）轨道、姿态、轴向振动耦合的动力学方程.采用辛Runge-Kutta方法对耦合动力学方程进行数值求解.数值结果表明：与经典的Runge-Kutta方法相比，辛Runge-Kutta方法可以长时间保持ISC系统的能量，并且相对能量误差一直保持在同一数量级.因此，采用辛算法研究ISC系统动力学问题，可以为探索研究其长期在轨运行提供很好的参考依据.

1 动力学建模

图1所示是20世纪90年代末NASA提出的ISC，该系统的优点是将微波发射天线和太阳电池阵布置在很近的位置，可以达到减少电力传输系统的质量和体积，降低成本的目的［3-4］.根据Malla等人的工作，将ISC抽象成哑铃模型.如图2所示，建立坐标原点为地心O的惯性坐标系OXYZ，其中OX轴与赤道的长半轴重合，OZ轴垂直于赤道平面，OY轴由右手法则得到.ISC的质心O′的轨道半径设为r，真近点角为θ，姿态角设为φ.模型的主要假设如下：

（1）将连接两端薄膜反射镜的桅杆抽象为可以伸缩但是不可以弯曲、不计质量的细长杆；

（2）假设ISC的全部质量集中在细长杆的两端，分别为m1和m2；

（3）假设ISC在赤道平面运行，只考虑地球带谐项J2摄动和田谐项J2，2摄动.

图1 集成对称聚光系统示意图Fig.1 Integrated symmetrical concentrator

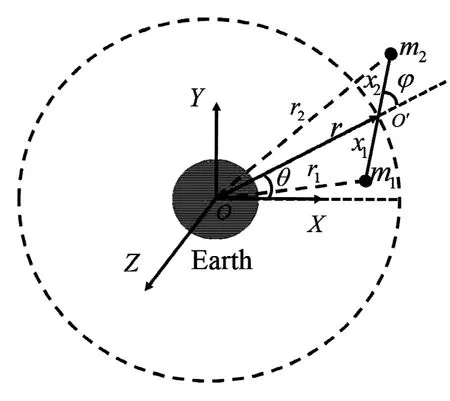
图2 集成对称聚光系统动力学模型Fig.2 Model of integrated symmetrical concentrator

设xi（i＝1，2）是质量为mi（i＝1，2）的质点到质心O′的距离，则

其中，x是杆的长度，m＝m1+m2.设ri（i＝1，2）是质量为mi（i＝1，2）的质点到地心O的距离，则

1.1 模型的势能

由于地球并非是标准的球体，因此地球的非球形摄动位函数在固坐标系中可以展成球谐函数的形式.假设ISC在赤道平面半长轴上方同步运行，则要同时考虑带谐项和田谐项摄动的影响，取二阶摄动项J2和J2，2时，模型的势能可以表示为［11，21］：

目前，三方共同创新研制了名为“智宝”的移动式病虫害智能化感知设备，填补了国内外移动式病虫害智能测报技术与产品的空白。该设备集成了包括视觉、温湿度传感器、地理位置、移动终端等多种信息获取手段，有效提升了现有病虫害监测能力。

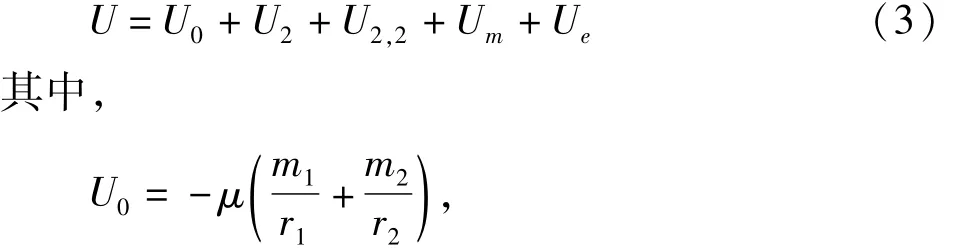
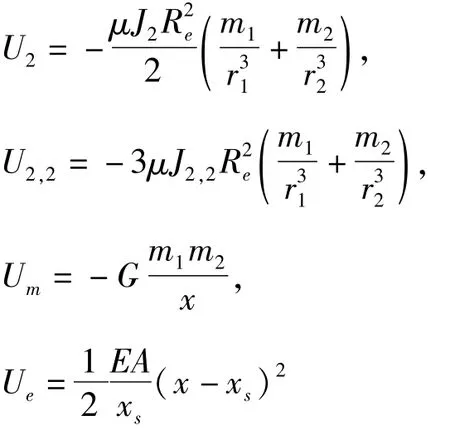
其中，E、A、xs分别为杆的弹性模量、横截面积、自然长度，μ为地心引力常数，G为引力常数，Re为地球赤道半径.

1.2 模型的动能

ISC模型的动能包括平动动能和转动动能，可以表示为［11］

1.3 模型的Hamilton体系表示

建立动力学问题方程的方法大体上可以分为两种：一是以Newton定律为基础的矢量力学方法，二是以变分原理为基础的分析力学方法.对于分析力学又可以分为Lagrange体系的表述和Hamilton体系的表述.虽然在这两种体系下得到的动力学方程是等价的，但是后者在数值方程的导入时更方便，在数值求解时计算效率更高，在系统本身性质的保持上会更好［22-23］.对于保守体系，为了得到辛算法，就应该在Hamilton体系的框架下建立动力学方程.Hamilton体系的数学框架是辛几何，因此应该通过正则变换导入到辛几何框架内进行计算.下面导出保守Hamilton体系的正则方程，首先通过Legendre变换引入广义动量，为了便于书写，引入广义坐标向量和广义速度向量，分别表示为

对于只考虑保守力的ISC，则其总能量以及角动量应该得到保持，即Hamilton函数H（q，p）＝const.，角动量pθ＝const..由方程（12）可以看到，ISC的角动量的导数为零，说明其角动量是守恒的.

2 ISC轨道、姿态、轴向振动的耦合动力学分析

2.1 初始条件

设ISC在地球的同步轨道运行，初始值为r0＝4.227433×107m，θ0＝0.0rad，φ0＝0rad，x0＝1.0416×104m，˙r0＝0.0m/s，˙θ0＝7.263631835029276 ×10-5rad/s，˙φ0＝0.0rad/s，˙x0＝0.0m/s.

2.2 地球的非球形摄动的影响

由于地球的形状和密度分布是不均匀的，而ISC要在轨运行30～40年，所以地球的非球形摄动是一种不可忽视的摄动源.假设无摄动、J2摄动、J2，2摄动下系统的能量分别为H、H2、H22，定义其相应的相对能量误差分别为，其中下标0表示初始时刻的能量.为了表述方便，本节的一些标记如表1所示.

表1 标记Table 1 Nomenclature

下面给出10个轨道周期内的分析结果.图3给出了利用辛Runge-Kutta方法计算得到的ISC系统的相对能量误差图.从图3中可以看出在Hamilton体系下，不管是否考虑地球的非球形摄动，利用辛Runge-Kutta方法计算得到的该系统的相对能量误差都是10-15量级，并且一直保持该数量级.图4给出的是利用经典Runge-Kutta方法计算得到的相对能量误差图.从图4中可以看出不管是否考虑地球的非球形摄动，相对能量误差精度都比辛Runge-Kutta方法低3个量级，并且相对能量误差呈现线性增长的趋势，说明辛算法在保能量方面有突出的优势.图5给出了地球的非球形摄动的影响下，ISC质心半径的变化情况.由于地球的J2摄动，ISC的质心轨迹不再是严格的圆，变成了偏心率很小的椭圆，从而质心半径会有3122m的最大偏移；同样，地球的J2，2摄动也会引起ISC的质心半径的变化，质心半径的最大偏移量是31m.图6给出了地球的非球形摄动的影响下，ISC真近点角的变化情况.在地球的J2摄动和J2，2摄动下，真近点角比未考虑摄动时都有所增大，虽然影响比较小，但这种趋势是线性增长的.图7给出了地球的非球形摄动的影响下，ISC姿态角的变化情况.即使无摄动力时，姿态角也会发生周期性的振荡，当考虑J2摄动和J2，2摄动时，姿态角都会有小幅的影响.图8给出了地球的非球形摄动的影响下，ISC杆长的变化情况.在不考虑摄动力时，杆长会周期性的伸长和缩短，当考虑摄动时，虽然对于长度变化的影响不是很大，但一直在增加，这对于长时间在轨运行的ISC是值得仔细考虑的.

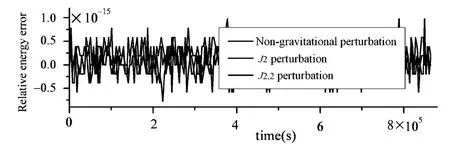
图3 相对能量误差（辛Runge-Kutta方法）Fig.3 Error of relative energy through symplectic Runge-Kuttamethod

图4 相对能量误差（经典Runge-Kutta方法）Fig.4 Error of relative energy through classical Runge-Kuttamethod

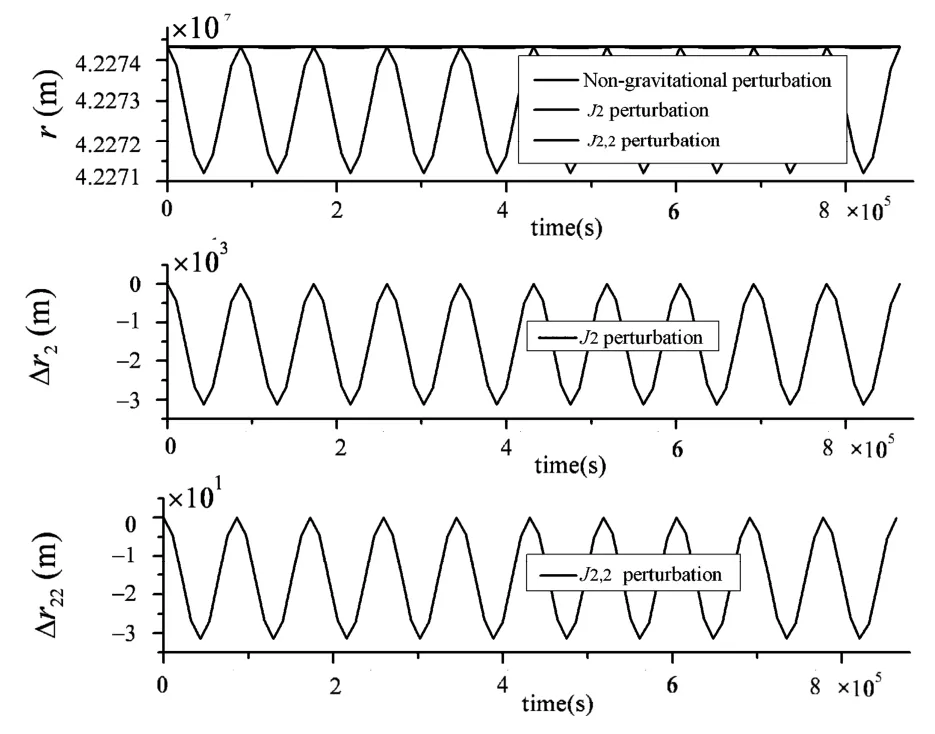
图5 引力摄动力对轨道半径的影响Fig.5 Effect of the gravitational perturbation on orbit radius

图6 引力摄动力对真近点角的影响Fig.6 Effect of the gravitational perturbation on true anomaly

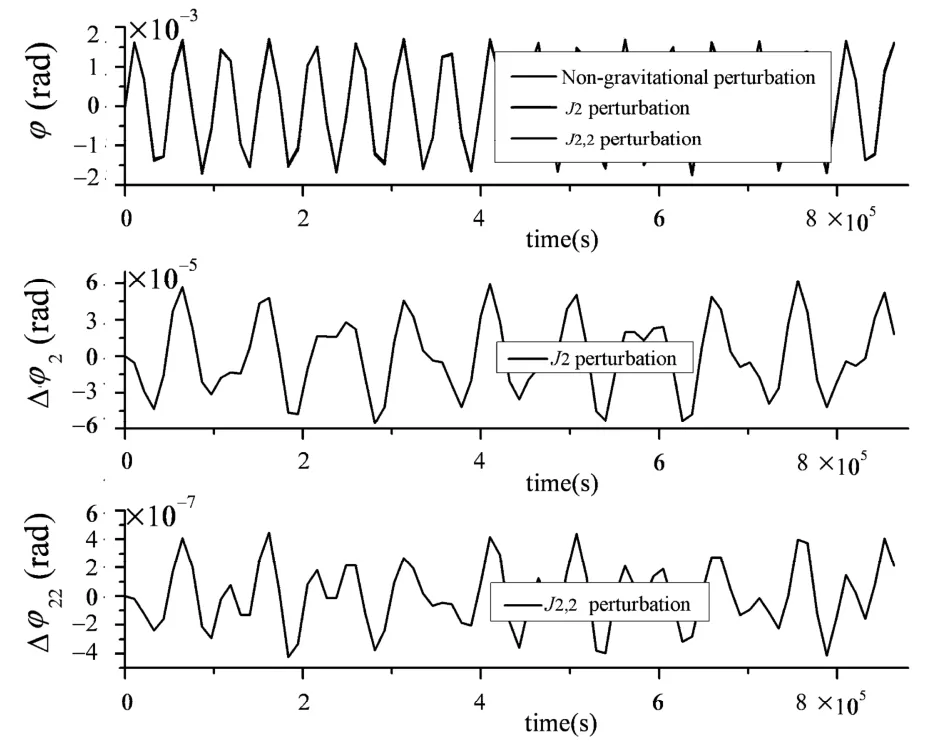
图7 引力摄动力对姿态角的影响Fig.7 Effect of the gravitational perturbation on attitude angle

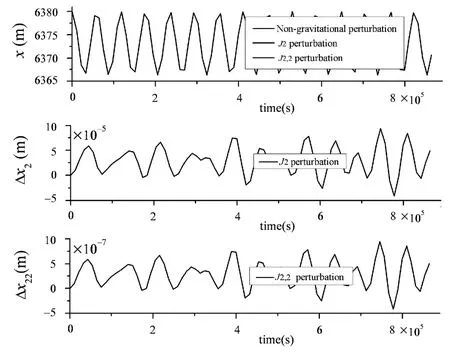
图8 引力摄动力对轴向变形的影响Fig.8 Effect of the gravitational perturbation on axial deformation

3 结论

本文通过Legendre变换引入了广义动量，将方程导入了Hamilton体系，建立了轨道、姿态、轴

向振动耦合的动力学方程，并采用辛Runge-Kutta方法进行了数值求解.通过数值结果分析了地球的J2和J2，2摄动项对ISC的轨道、姿态、轴向振动以及系统总能量的影响.

研究结果表明：在保守的Hamilton体系下ISC的角动量守恒是自动保持的.利用辛Runge-Kutta方法对耦合动力学方程进行数值求解，可以长时间保持ISC系统的能量，能量相对误差只有10-15量级.然而经典Runge-Kutta方法不能保持系统的能量，相对能量误差精度会低3个量级，并且相对能量误差会呈现线性的增长.说明Hamilton体系下的辛算法在保结构方面有突出的优势.地球的非球形摄动对轨道、姿态以及轴向变形都会产生影响，而对于轨道的影响最显著.因此，对于ISC这样一个轨道、姿态、弹性振动耦合的复杂问题，研究其在地球摄动力的影响下的耦合效应是十分必要的，为探索研究其长期在轨运行提供了很好的参考依据.

1 Koomanoff F A，Bloomquist C E.The satellite power system：concept development and evaluation programme.In：Glaser P E，Davidson F P，Csigi K I，Solar Power Satellites：A Space Energy System for Earth，Praxis Publishing，Wiley，Chichester，1998：23～56

2 Mankins JC.SPS-ALPHA：The first practical solar power satellite via arbitrarily large phased array（a 2011-2012 NASA NIAC Phase 1 Project），Artemis Innovation Management Solutions LLC，Santa Maria，California，2012

3 王新栋，胡伟鹏，邓子辰.空间太阳能电站太阳能接收器二维展开过程的保结构分析.动力学与控制学报，2015，13（6）：405～408（Wang X D，Hu W P，Deng Z C. Structure-preserving analysis of 2D deploying process for solar power receiver of solar power satellite.Journal of Dynamics and Control，2015，13（6）：405～408（in Chinese））

4 王立，侯欣宾.空间太阳能电站的关键技术及发展建议.航天器环境工程，2014，31（4）：343～350（Wang L，Hou X B.Key technologies and some suggestions for the development of space solar power station.Spacecraft Environment Engineering，2014，31（4）：343～350（in Chinese））

5 Sasaki S，Tanaka K，Higuchi K，et al.A new concept of solar power satellite：Tethered-SPS.Acta Astronautica，2006，60（3）：153～165

6 闫勇，金光.空间太阳能电站发展及研究.中国光学，2013，6（2）：129～135（Yan Y，Jin G.Development and research of solar power systems.Chinese Optics，2013，6（2）：129～135（in Chinese））

7 荆武兴，杨涤，吴瑶华等.引力引起的空间站轨道与姿态耦合动力学方程的建立和计算.哈尔滨工业大学学报，1991，1（3）：53～59（Jing W X，Yang D，Wu Y H，et al. Derivation and calculation of gravitational orbit-attitude coupling dynamic equations of space station.Journal of Harbin Institute of Technology，1991，1（3）：53～59（in Chinese））

8 Wie B，Roithmayr CM.Attitude and orbit control ofa very large geostationary solar power satellite.Journal of Guidance，Control，and Dynamics，2005，28（3）：439～451

9 McNally I，Scheeres D，Radice G，et al.Orbital dynamics of large solar power satellites.In：64th International Astronautical Congress，Paper IAC-13-C3.1.7，Beijing，Sept. 2013

10 McNally I，Scheeres D，Radice G.Attitude dynamics of large geosynchronous solar power satellites.In：AIAA/AAS Astrodynamics Specialist Conference，AIAA，San Diego，CA，Aug.2014

11 Malla，R B，Nash W A，Lardner T J，Motion and deformation of very large space structures.AIAA Journal，1989，27（3）：374～376

12 Malla R B.Structural and orbital conditions on response of large space structures.Journal of Aerospace Engineering，1993，6（2）：115～132

13 Ishimura K，Higuchi K.Coupling between structural deformation and attitude motion of large planar space structures suspended bymulti-tethers.Acta Astronautica，2007，60（8）：691～710

14 Ishimura K，HiguchiK.Coupling among pitchmotion，axial vibration，and orbitalmotion of large space structures. Journal of Aerospace Engineering，2008，21（2）：61～71

15冯康，秦孟兆.Hamilton动力体系的Hamilton算法.自然科学进展，1991，1（2）：102～112（Feng K，Qin M Z. Hamiltonian algorithms for Hamiltonian dynamical systems.Progress in Natural Science，1991，1（2）：102～112（in Chinese））

16冯康，秦孟兆.哈密顿尔系统的辛几何算法.杭州：浙江科学技术出版社，2003（Feng K，Qin M Z.Symplectic geometric algorithms for Hamiltonian systems.Hangzhou：Zhejiang Science＆Technology Press，2003（in Chinese））

17张素英.非线性动力学系统一般形式及其广义哈密顿体系下的几何积分方法［博士学位论文］.西安：西北工业大学，2003（Zhang SY.Geometric integrationmethods for generalized Hamiltonian systems and furthermore for general nonlinear dynamic systems［PhD Thesis］.Xi′an：Northwestern Polytechnical University，2003（in Chinese））

18 Hairer E，Lubich C，Wanner G.Geometric numerical integration：structure-preserving algorithms for ordinary differential equations.Berlin：Springer，2006

19钟万勰.应用力学的辛数学方法.北京：高等教育出版社，2006（ZhongW X.Symplectic solutionmethodology in applied mechanics.Beijing：Higher Education Press，2006（in Chinese））

20赵长印，廖新浩，刘林.辛积分方法在动力天文中的应用.天文学报，1992，33（1）：36～47（Zhao Z Y，Liao X H，Liu L.Application of symplectic integrators to dynamical astronomy.Acta Astronomica Sinica，1992，33（1）：36～47（in Chinese））

21章仁为.卫星轨道姿态动力学与控制.北京：北京航空航天大学出版社，1998（Zhang R W.Orbit attitude dynamics and control of satellite.Beijing：Beijing University of Aeronautics and Astronautics Publishing House，1998（in Chinese））

22陈滨.分析动力学.北京：北京大学出版社，2012（Chen B.Analytical dynamics.Beijing：Peking University Press，2012（in Chinese））

23王琪，陆启韶.多体系统Lagrange方程数值算法的研究进展.力学进展，2001，31（1）：9～17（Wang Q，Lu Q S. Advances in the numerical methods for Lagrange′s equations ofmultibody systems.Advances in Mechanics，2001，31（1）：9～17（in Chinese））

24 Carrington C，Fikes J，Gerry M，etal.The abacus/reflector and integrated symmetrical concentrator：concepts for space solar power collection and transmission.In：The 35th Intersociety Energy Conversion Engineering Conference and Exhibit，AIAA～2000～3067，Las Vegas，July，2000

25李恒年.地球静止卫星轨道与共位控制技术.北京：国防工业出版社，2010（Li H N.Geostationary satellite orbital analysis and collocation strategies.Beijing：National Defence Industry Press，2010（in Chinese））

26刘林.航天器轨道理论.北京：国防工业出版社，2000（Liu L.Spacecraftorbit theory.Beijing：National Defence Industry Press，2000（in Chinese） ）

COUPLING DYNAM IC MODELING AMONG ORBITAL MOTION，ATTITUDE MOTION AND STRUCTURAL VIBRATION AND SYMPLECTIC SOLUTION OF SPS*

Wei Yi Deng Zichen†Li Qingjun Wen Fenqiang
（Department of Engineering Mechanics，Northwestern Polytechnical University，Xi′an 710072，China）

As a system to collect clean energy from outer space，the solar power satellite（SPS）has attracted great concerns of various countries and scientific research institutions in theworld.As SPS is a very large flexible and lightweight structure in outer space，it is necessary to investigate the coupling effect of orbitalmotion，attitudemotion and structural vibration in the study of the global dynamics.In this paper，under the consideration of the effects of the non-gravitational perturbation forces，the coupled orbital，attitude and structural Hamiltonian equations of the integrated symmetrical concentrator（ISC）are constructed by using Legendre transformation and introducing generalized momenta.Subsequently，the dynamic equations of the system are solved by the symplectic Runge-Kuttamethod.According to the numerical results，the effects of non-gravitational perturbation of order 2 are well discussed，and the variation of total energy is analyzed.

solar power satellite， orbit， attitude， structure vibration， symplectic

10.6052/1672-6553-2016-021

2015-12-27收到第1稿，2016-03-12收到修改稿.

*国家自然科学基金（11432010，11572254，11502202），高校博士点基金（20126102110023），西北工业大学博士论文创新基金（CX201517）资助项目

†通讯作者E-mail：dweifan＠nwpu.edu.cn

Received 27 December 2015，revised 12 March 2016.

*The project supported by the National Natural Science Foundation of China（11432010，11572254，11502202），the Doctoral Program Foundation of Education Ministry of China（20126102110023），and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University（CX201517）

†Corresponding author E-mail：dweifan＠nwpu.edu.cn