最小二乘法在高斯拘束函数求解中的应用*

袁萍萍戈新生

（1.北京信息科技大学机电工程学院，北京 100192）（2.北京信息科技大学理学院，北京 100192）

最小二乘法在高斯拘束函数求解中的应用*

袁萍萍1†戈新生2

（1.北京信息科技大学机电工程学院，北京 100192）（2.北京信息科技大学理学院，北京 100192）

高斯最小拘束原理是一种典型的微分变分原理，以加速度为变量，通过寻求拘束函数极值的变分方法直接得出系统的运动规律.目前，国内常用的求解高斯拘束函数的方法为拉格朗日乘子法，通过引入拉格朗日乘子将高斯拘束函数的条件极值问题转化为带有拉格朗日乘子的无条件极值问题，这种求解方法会增加未知变量的个数.为减少变量个数，进一步提高运算效率，文章首先对高斯拘束函数进行简单变形，引入加速度形式的约束方程将高斯拘束函数化为最小二乘形式，直接运用最小二乘法导出使高斯拘束函数取极小值时系统真实加速度的表达式.最后通过对曲柄滑块机构正动力学问题的分析和计算，验证了该方法的有效性.

多体系统， 动力学建模， 高斯最小拘束原理， 最小二乘法， 曲柄滑块机构

引言

多体系统动力学广泛应用于航天、机械、兵器、车辆等领域，为分析多体系统的运动性能及优化设计提供了有力的理论支撑.多体系统动力学的研究包括系统动力学模型的建立和提高模型求解的速度、稳定性和精度等内容.栗鹏和姚文丽［1］以共线三球链的碰撞动力学为例，建立其碰撞的Hertz模型并进一步研究了求解的数值算法.目前，常用的解决多体系统动力学问题的方法有：牛顿-欧拉方法、罗伯逊-维登伯格方法、拉格朗日方法和高斯最小拘束原理等.高斯最小拘束原理属于微分变分原理，变分的力学原理是将系统的真实运动与可能发生的运动进行区分并加以比较.高斯最小拘束函数以系统的加速度为变量，在满足约束方程的系统所有可能加速度中，真实加速度使拘束函数取极小值［2］.运用高斯最小拘束原理可以直接得出系统的运动规律.近年来，陈小平、冯祖仁等［3］将高斯最小拘束原理应用于端杆加速度受约束的机器人动力学分析和建模中，得出机器人关节加速度的线性递推公式.史跃东和王德石［4］运用高斯最小拘束原理建立了火炮系统的动力学模型，进行了火炮射击过程的数值仿真和振动分析，并确定了影响炮口振动的主要因素以及火炮系统的固有振动频率.董龙雷、闫桂荣等［5］结合有限段法和高斯最小拘束原理对一类刚柔混合系统进行描述，比较完整的反映了系统的运动学特征.姚文丽和戴葆青［6］从相对质点形式的变分形式推导出广义坐标形式的高斯最小拘束原理，并给出了非理想约束、单边约束及刚体碰撞情形下的高斯最小拘束函数表达式.刘延柱、薛纭［7］建立了基于高斯原理的Cosserat弹性杆的分析力学模型，导出了拘束函数的普遍形式，将弹性杆的相应约束对可能运动施加限制，避免弹性杆空间自相侵占情况的发生.Kalaba［8］运用拉格朗日方程的一般形式推出高斯最小拘束函数表达式，并导出满足约束条件的系统加速度表达式.Herman和Oussama［9］将高斯最小拘束原理应用于冗余系统中，导出冗余机器人的动力学方程.Fan和Kalaba［10］将高斯最小拘束原理运用到非理想约束系统中，分析非理想约束力，如摩擦力，对系统运动精度的影响.

目前，论文中常用的求解高斯拘束函数的拉格朗日乘子法，需引入h个拉格朗日乘子λi（i＝1，2，…，h），其中h为约束方程的个数，虽然此方法可以将高斯拘束函数的条件极值问题转化为无条件极值问题，但是相应的增加了h个未知变量，降低了计算效率，为避免引入多余的未知变量，文章试图寻求一种新的求解高斯拘束函数的方法.

通过简单的变形运算，将求高斯拘束函数最小值问题变形为最小二乘问题.根据系统的真实加速度满足约束方程且使拘束函数取极小值，运用最小二乘法导出系统真实加速度的表达式，对系统的真实加速度进行积分运算便可得到系统的真实运动规律.最后运用推导出的系统真实加速度的显示表达式，对曲柄滑块机构进行动力学分析及计算，得到其运动规律，验证该求解方法的有效性.

1 高斯最小拘束函数

高斯最小拘束函数以加速度为变量，在任意时刻t，系统的真实运动与符合系统约束的所有可能发生的运动相比较，系统的真实加速度使其拘束函数取极小值.

高斯最小拘束函数G的表达式为［8］

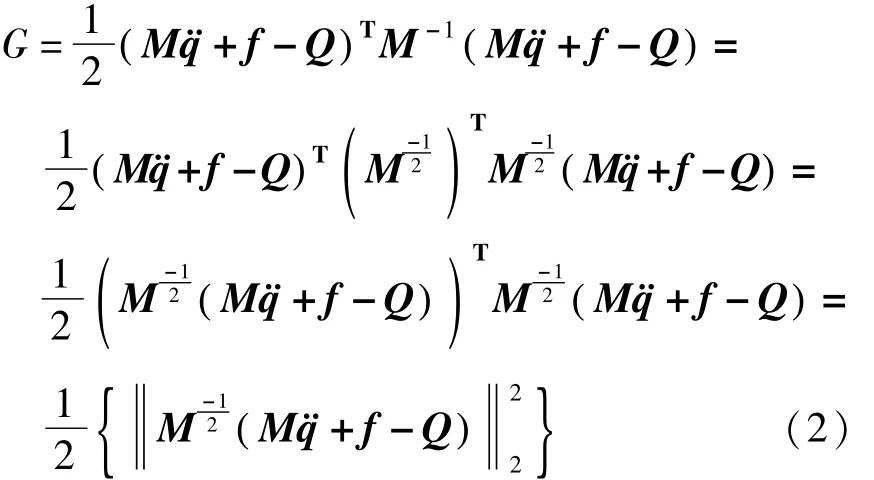
式（2）为高斯最小拘束函数的另一种表达形式.式（1）和（2）考虑了系统所受理想约束的条件.当Qc为非理想广义约束力时，可将非理想约束力视为系统主动力的一部分，此时高斯最小拘束函数为

2 系统的约束方程

运用高斯最小拘束原理求解多体系统的运动规律，其系统的约束方程可以是完整的也可以是非完整的.设系统受到d个完整约束、g个非完整约束，其形式可写为

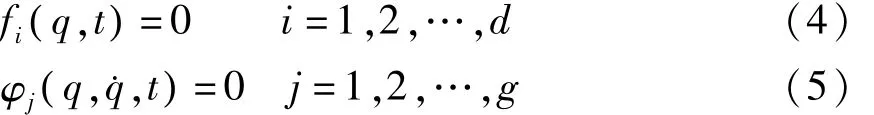
将式（4）对时间求两次微分和式（5）对时间求一次微分，所得结果可写为矩阵形式

3 求解高斯最小拘束函数中加速度

4 仿真算例

以曲柄滑块机构为例，如图（1）所示.图中o1，o2和o3分别为曲柄、连杆和滑块的质心，曲柄、连杆和滑块的连体坐标系建立在其质心处，惯性坐标系建立在点o处，曲柄和连杆的连体坐标系和惯性坐标系之间的夹角分别为θ1，θ2.系统的广义坐标为：q＝［x1，y1，θ1，x2，y2，θ2，x3］T.曲柄在转动副o处施加有转矩τ＝-0.5N·m.滑块末端连接有弹簧阻尼器，刚度系数为k＝5N/m，阻尼系数为c＝1N·s/m.当θ1＝θ2＝0时，弹簧处于平衡位置.设m1，m2和m3分别为曲柄、连杆和滑块的质量，m1＝0.37kg，m2＝0.77kg，m3＝0.1kg；l1和l2分别为曲柄和连杆的长度，l1＝0.15m，l2＝0.56m；g为重力加速度.

图1 曲滑块机构Fig.1 Crank slidermechanism

曲柄滑块机构的广义质量矩阵M，广义力向量Q分别为

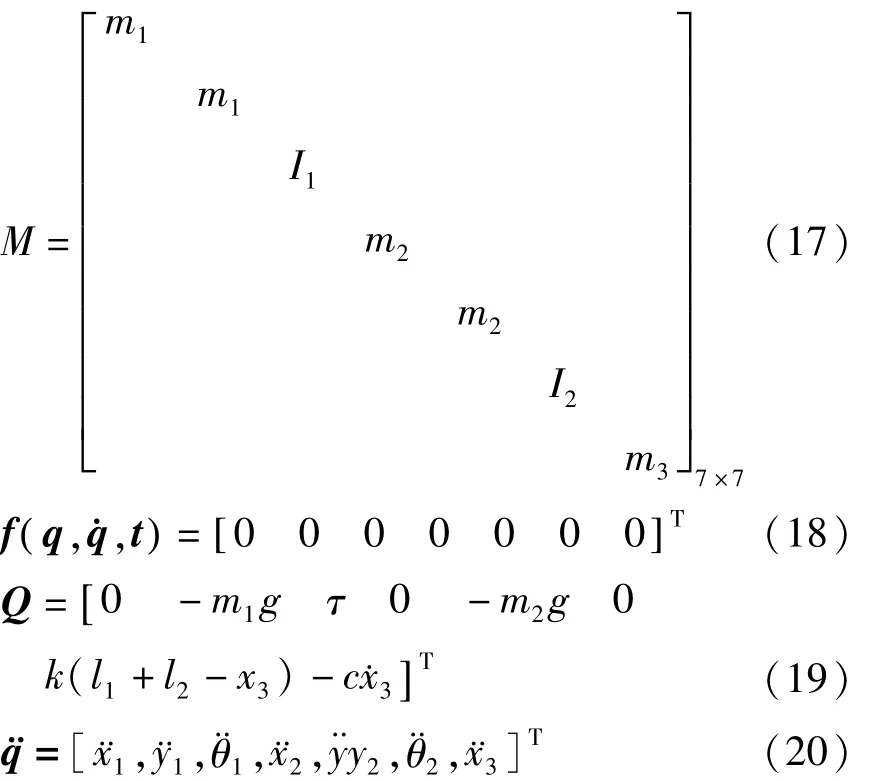
系统的约束方程为

设系统的初始条件分别为

将式（17）、（18）、（19）、（20）代入式（3），得到曲柄滑块机构的拘束函数表达式.引入约束方程φ，通过式（16）求解得出曲柄滑块机构的位移和速度变化规律图.

图1～5分别为曲柄质心在X，Y方向上的位移、速度变化曲线.图6～7为曲柄转角与曲柄转动角速度的变化曲线.图8～9为滑块质心在X方向的位移、速度变化曲线.曲柄滑块机构中存在阻尼为耗散机构，滑块的运动幅度和速度会随时间逐渐减小，机构最终在一平衡状态停止运动.

图2 曲柄质心X轴方向位移Fig.2 Deformation of the crank shaft in X axis direction

图3 曲柄质心X轴方向速度Fig.3 Velocity of Crank center in X direction

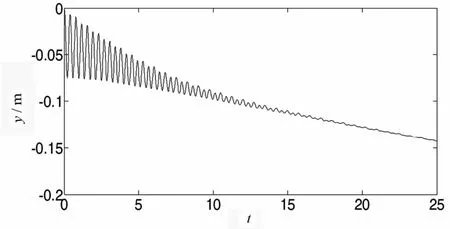
图4 曲柄质心Y轴方向位移Fig.4 Displacement of crank Center in Y direction

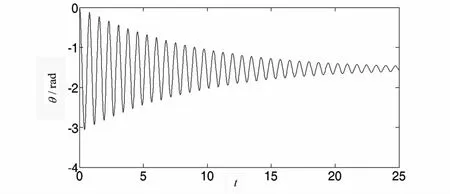
图6 曲柄转角随时间的变化规律Fig.6 Time history of the crank angle

图7 曲柄转动角速度Fig.7 Angular velocity of Crank

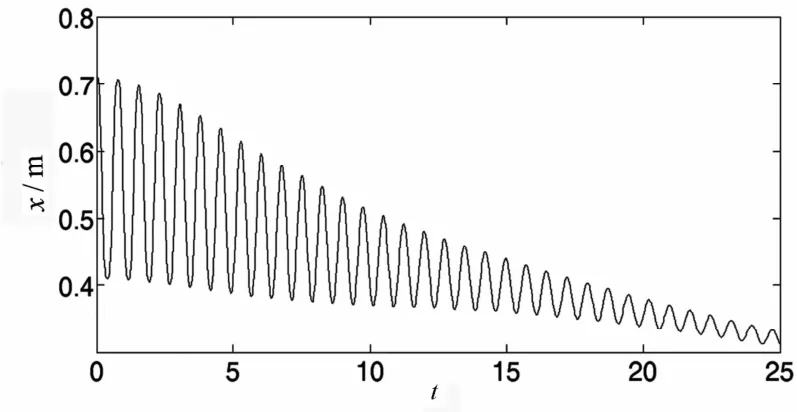
图8 滑块X轴方向的位移Fig.8 Displacement of the slider in X direction

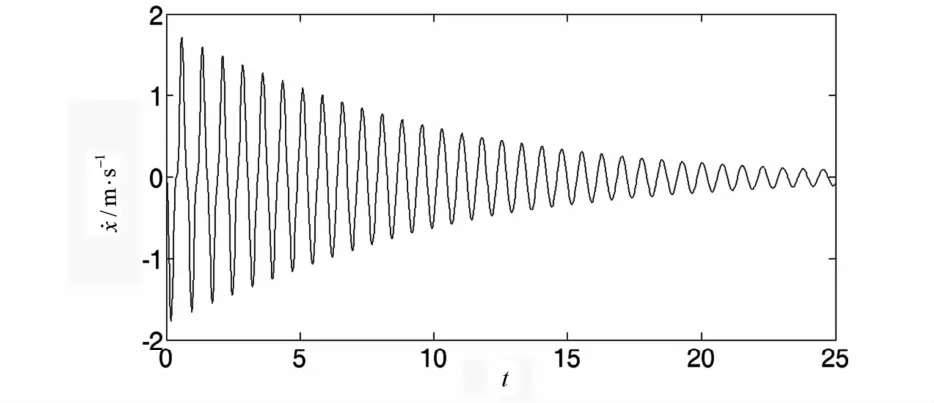
图9 滑块X轴方向的速度Fig.9 Velocity of the slider in X direction

5 小结

高斯最小拘束原理不直接描述系统的机械运动规律，而是把真实发生的运动与可能发生的运动加以比较，在相同条件下所发生的很多的可能运动中指出真实运动所应满足的极值条件，用高斯最小拘束原理求解多体系统动力学问题，主要优点是可以利用各种有效的数学规划方法寻求高斯拘束函数的极值，且不论是树形的还是非树形的系统，都可以用同样的方法处理.文章利用最小二乘法对高斯拘束函数进行求解，直接得到了系统真实运动的加速度表达式，且不需要引入其它辅助变量.从曲柄滑块机构的仿真结果可以看出，系统的数学模型推导简单，形式统一，而且能够得到多体系统运动规律的精确解，计算效率高，方法简单，易于程式化.本文提供了一种统一而有效的多体系统动力学分析与计算方法.

1 栗鹏，姚文丽.共线三球链问题的碰撞动力学研究.动力学与控制学报，2013，11（4）：301～305（Li P，YaoW L. Study on collinear collision dynamics of the three-ball chain.Journal of Dynamicsand Control，2013，11（4）：301～305（in Chinese））

2 刘延柱.高等动力学.北京：高等教育出版社，2001（Liu Y Z.Higher dynamics.Beijing：Higher Education Press，2001（in Chinese））

3 陈小平，冯祖仁，胡保生.一种新的基于spatial高斯最小拘束原理的正动力学算法.机器人，1992，14（2）：45～51（Chen X P，Feng Z R，Hu B S.A new positive dynamic algorithm based on the principle of spatial Gauss. Robot，1992，14（2）：45～51（in Chinese））

4 史跃东，王德石.高斯最小拘束原理在火炮振动分析中的应用.火炮发射与控制学报，2009（4）：26～30（Shi Y J，Wang D S.Gaussianminimum binding principle in Gun Vibration Analysis.Gun Launch＆Control，2009（4）：26～30（in Chinese））

5 董龙雷，闫桂荣等.高斯最小拘束原理在一类刚柔耦合系统分析中的应用.兵工学报，2001，22（3）：347～351（Dong L L，Yan GR，Du Y T.Gaussianminimum binding principle in a class of rigid coupling system analysis.Industry and Technololgy，2001，22（3）：347～351（in Chinese））

6 姚文莉，戴葆青.广义坐标形式的高斯最小拘束原理及其推广.力学与实践，2014，36（6）：779～785（Yao W L，Dai B Q.Generalized coordinates Gaussian minimum binding principle and its promotion.Mechanics in Engineering，2014，36（6）：779～785（in Chinese））

7 刘延柱，薛纭.基于高斯原理的Cosserat弹性杆动力学模型.物理学报，2015，64（4）：1～5（Liu Y Z，Xue Y.Dynamic model of Cosserat elastic rod based on gauss principle.Journal of Physics，2015，64（4）：1～5（in Chinese））

8 Kalaba R E，Udwadia F E.Equations ofmotion for nonholonomic，constrained dynamical systems via gauss′s principle. Journal of Applied Mechanics，1993，60（3）：662～668

9 Herman B，Oussama K.Gauss′s principle and the dynamicsof redundant and constrained manipulators.International Conference on Robotics＆Automation，2000，3：2563～2568

10 Fan Y Y，Kalaba R E.Reflections on the gauss principle of least constraint.Journal of Optimization Theory and Applications，2005，127（3）：475～484

11戴中林.广义逆矩阵A-的计算方法及应用.大学数学，2014，30（6）：56～59（Dai Z L.The calculation method of generalized inversematrix A-and its application.University Mathematics，2014，30（6）：56～59（in Chinese））

12李庆扬，王能超等.数值分析.北京：清华大学出版社，2001（LiQ Y，Wang N C，Yi D Y.Numerical analysis. Beijing：Tsinghua University Press，2001（in Chinese） ）

APPLICATION OF LEAST SUQARE METHOD IN SOLVING GAUSS CONSTRAINT FUNCTION*

Yuan Pingping1†Ge Xinsheng2
（1.School of Mechanical and Electrical Engineering，Beijing Information Science and Technology University，Beijing 100192，China）
（2.School of Applied Science，Beijing Information Science and Technology University，Beijing 100192，China）

Gauss′sminimum constraint principle is a typical differential variation principle，where the acceleration is the variable，and themotion law of the system can be obtained directly by the variationmethod of seeking the extreme of the constraint function.At present，Lagrange multiplier method is widely used for solving the Gauss constraint function.Through the introduction of Lagrangemultipliers，the conditional extreme value problem of Gauss constraint function is transformed to the unconditional extreme problem.However，thismethod increase the number of unknown variables.In order to reduce the number of variables，it need further study to improve the operation efficiency.In this paper，the deformation on Gauss constraint function is firstly simplified. The constraint equations of the acceleration form are also introduced into the Gauss constraint equations to get the least square form of equations.The least squaremethod is then used to export the expression of the true acceleration of the system，which canmake the Gauss binding function to take theminimum value.In the end，the validity of themethod is verified by analyzing and calculating the normal dynamics of the crank slidermechanism.

multi-body system， dynamic modeling， Gauss′sminimum constraint principle， Least square method， Crank slidermechanism

10.6052/1672-6553-2016-003

2015-10-08收到第1稿，2015-12-08收到修改稿.

*国家自然科学基金资助项目（11472058）

†通讯作者E-mail：pingping861206＠163.com

Received 8 October 2015，revised 8 December 2015.

*The project supported by the National Natural Science Foundation of China（11472058）

†Corresponding author E-mail：pingping861206＠163.com