长距离有压输水管道阀门关闭规律研究
□康迎宾 □张学林 □徐杨洋(华北水利水电大学)
长距离有压输水管道阀门关闭规律研究
□康迎宾□张学林□徐杨洋(华北水利水电大学)
摘要:长距离有压输水工程中的水锤压力,是影响供水工程安全运行的重要因素之一,末端阀门的关闭引起的水锤问题是最常见而又最突出。针对长距离有压输水管道末端阀门关闭引起的水锤问题,以特征线法为理论基础,以南水北调中线某配套工程有压输水管线为例,分别对该管线末端阀门在直线关阀和先快后慢两阶段关阀两种工况下的水锤压力进行计算,进而对末端阀门的关闭规律进行优化分析。结果表明,优化阀门的关闭规律可有效的降低长距离有压输水管道系统的水锤压力。
关键词:压力管道;阀门关闭规律;水锤计算;优化分析
0 前言
近年来,长距离输水工程在中国日渐增多,所用的输水方式以有压输水管道居多,尤其随着南水北调工程配套工程的建设,其运用越来越广。在长距离有压输水管道工程中,末端阀门的关闭引起的水锤问题是最常见而又最突出。对长距离有压管道系统,一般采用装设调压塔和空气阀等进行水锤防护。同时,正确的分析和计算压力管道的水锤,对提高压力管道设计水平、确保系统安全运行具有十分重要的意义。文章在前人研究的基础上,结合南水北调中线某配套工程有压输水管线,通过对末端阀门的关闭规律进行优化分析,确定阀门的最优关闭规律,以降低有压输水管道系统中的水锤压力。
1 水锤计算的特征相容方程
水锤基本方程理论基础是水流动的力学规律和连续原理,是水力过渡过程分析研究的基础。它包含以微分方程表示的运动方程和连续方程,反映了在水力过渡过程中不稳定水流的流速和水头的变化规律,水锤基本方程表达式如下:
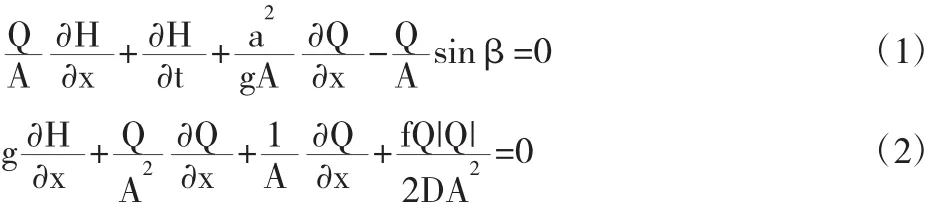
式中:H为测压管水头;Q为流量;D为管道直径;A为管道面积;t为时间变量;a为水锤波速;g为重力加速度;x为沿管轴线的距离;f为摩阻系数;β为管轴线与水平面的夹角。
式(1)、(2)可简化为标准的双曲型偏微分方程,从而可利用特征线法将其转化成同解的管道水锤计算特征相容方程。
对于长度L的管道A—B,其两端点A、B边界在t时刻的瞬态水头HA(t)、HB(t)和瞬态流量QA(t)、QB(t)可建立如下特征相容方程:


其中:CM=HB(t-kΔt)-(a/gA)QB(t-kΔt);RM=a/gA+R|QB(t-kΔt)|;CP=HA(t-kΔt)-(a/gA)QA(t-kΔt);Rp=a/gA+R|QA(t-kΔt)|。
式中:Δt为计算时间步长;ΔL为特征线网格管段长度,ΔL=aΔt(库朗条件);k为特征线网格管段数,k=L/ΔL;R为水头损失系数,R=Δh/Q2;其它符号意义同前。
水力过渡过程计算一般从初始稳定状态开始,即取此时t=0,因此当式中(t-kΔt)<0时,则令(t-kΔt)=0,即取为初始值。式(3)、(4)均只有两个未知数,将其分别与A、B节点的边界条件联列计算,即可求得A、B节点的瞬态参数。
2 工程实例
2.1工程概况
南水北调中线配套某输水工程采用有压重力流,有压输水管线起始于分水口门,终止于末端水厂,全长26.03 km,设计流量0.50 m3/s,管径700 mm,采用球墨铸铁管。输水管线进口设计水位126.93 m,进口处压力管道中心高程122.15 m;末端水厂水位84.55 m,出口压力管道中心高程78.22 m。
有压输水管线沿线设53个空气阀和3个水锤消除器;主干线进口设控制阀,末端水厂设调流阀。工程管线布置如图1所示。
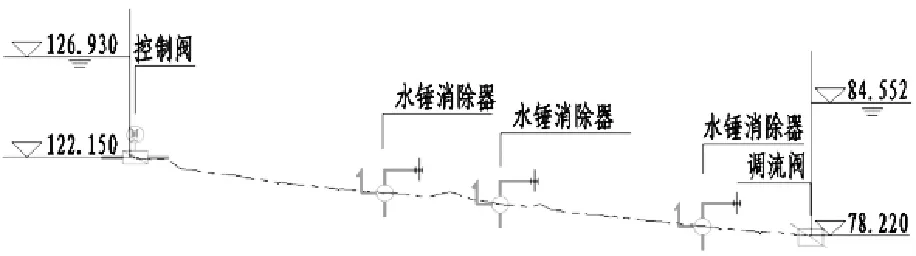
图1 工程管线布置图 (单位:m)
2.2计算结果及分析
2.2.1计算断面的选取
设定末端阀门关闭规律分别为匀速100 s关阀、匀速300 s关阀、匀速500 s关阀和匀速700 s关阀,计算有压管道沿线的水锤压力,结果如图2匀速100 s关阀图所示(匀速300 s关阀、匀速500 s关阀和匀速700 s关阀图略)。

图2 匀速100s关阀图
由图2分析可知,有压管道的水锤压力最大处位于距分水口门24.94km处,此处为穿河倒虹吸,因此选该断面作为计算断面。
2.2.2匀速关闭规律的分析
分别对匀速100 s关阀、匀速300 s关阀、匀速500 s关阀和匀速700 s关阀这几种工况下该断面的最大水锤压力随时间的变化情况进行计算,结果如图3匀速100 s关阀图所示(匀速300 s关阀、匀速500 s关阀和匀速700 s关阀图略)和表1所示。

图3 匀速100 s关阀图

表1 不同关阀时间下管道最大压力值表
由图3和表1可知,阀门关闭时间越长,最大水锤压力越小;但随着阀门关闭时间的逐渐延长,所产生的最大水锤压力得降幅会越来越小。
2.3先快后慢两阶段关闭规律的分析
选择500 s作为基准关阀时间以研究先快后慢两阶段关阀方式下的最大水锤压力。选择先快关70s,快关阶段阀门的关闭量为80%,然后再慢关至500 s全部关闭。通过水锤计算,可得该断面处的最大水锤压力为65.28 m H2O,此时该断面处压力随时间变化见图4所示。由此可知,相比匀速关阀,采用先快后慢两阶段关阀,最大水锤压力有明显的下降。
2.4先快后慢两阶段关闭规律的优化。
在上述先快后慢两阶段关闭规律计算的基础上,采用控制变量法,分别对快关阶段关闭时间和阀门关闭量进行计算分析。
固定快关阶段的阀门关闭量为80%,对快关阶段不同的关阀时间进行水锤计算,结果见表2和图5。
对表2和图5计算结果分析可知,固定快关阶段的关闭量,针对该阶段不同的关阀时间,快关时间越短,最大水锤压力越小。

图4 先快后慢两阶段关阀下管道最大压力随时间的变化图

表2 快关阶段不同关阀时间的计算结果表

图5 快关阶段不同关阀时间的计算结果分析图
固定快关阶段的关阀时间为50 s,对快关阶段的不同关闭量进行水锤计算,结果见表3和图6。

表3 快关阶段不同阀门关闭量的计算结果表
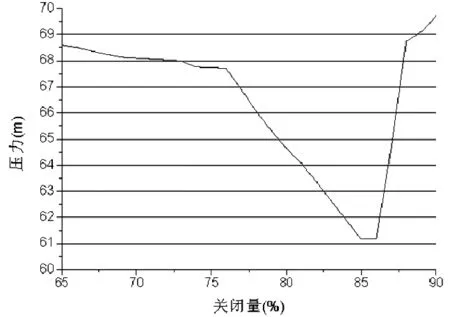
图6 快关阶段不同阀门关闭量的计算结果分析图
对表3和图6计算结果分析可知,固定快关阶段的关阀时间,对该阶段不同的阀门关闭量,其最大水锤压力也不同,存在最小值。快关阶段的关阀时间为50 s,阀门关闭量为85%时,最大水锤压力最小,为61.17 mH2O。
3 结语
对长距离有压输水管道系统,可通过控制阀门的关闭规律来降低系统最大水锤压力。通过上述分析,可得出以下结论:①阀门的关闭时间越长,最大水锤压力越小,但随着阀门关闭时间的逐渐延长,所产生的最大水锤压力得降幅会越来越小。②采用先快后慢两阶段关阀,可有效降低最大水锤压力。③采用先快后慢两阶段关阀时,快关阶段的关阀时间越短,最大水锤压力越小;对于不同的阀门关闭量,其最大水锤压力也不同,存在最小值,需要通过具体计算得出最小值。
(责任编辑:刘长垠韦诗佳)
收稿日期:2016-01-13
中图分类号:TV672. 2
文献标识码:A
文章编号; 1673-8853(2016)03-0068-02

