基于博弈论的旧城更新过程中多方利益均衡问题的研究

邵剑杰

（湖北理工学院土木建筑工程学院，湖北黄石435000）

基于博弈论的旧城更新过程中多方利益均衡问题的研究

邵剑杰

（湖北理工学院土木建筑工程学院，湖北黄石435000）

旧城更新是我国城镇一体化进程中不可忽视的问题，其牵涉到了社会的诸多层面。旧城更新的主要参与主体，包括地方政府、开发商、被拆迁者。参与主体在旧城更新过程中利益是否得到均衡，将会直接决定更新是否能够顺利地进行，运用博弈论的方法，建立三方博弈扩展式模型，可以分析三方的行为策略，并通过研究博弈均衡结果来探索实现三方共赢的方法。

旧城更新；博弈论；均衡

引言

旧城是以传统的社会生活为主体，以传统风貌作为重要特征，饱含着历史场所感的一种物质空间形态，其作为城市经济活动和文化活动等各种社会活动的中心，成为兼具城市人文景观和社会景观内涵的城市综合体，集中展现了城市的文化个性和地方特色［1］。

旧城的更新，是指将旧城里功能老化、布局不合理的已经不能适应现代化城市生活的地区所做出的有必要的、有计划的改建活动［2］。

旧城因其丰富的历史文化背景和举足轻重的社会地位，其更新问题会引起整个社会的关注，如何在更新开始前就均衡更新的各个参与主体的利益问题，是更新能否成功的关键。

一、旧城更新参与主体

旧城更新是一项牵涉社会诸多方面、涉及很多群体的利益的巨大工程，当面临局部改造或者是全面重建时，更新的主要参与主体之间需要相互的协调，才能保证更新过程的顺利完成，这些参与主体主要是：

（一）地方政府。地方政府是整个城市的管理者，是旧城更新的主导者，从立场上说，地方政府不管是出于自身政绩的需要，还是经济利益，都希望大力地推进旧城的更新，而在具体的更新过程中，他作为更新的宏观管理者，来指导、管理以及控制整个更新的过程［3］。

（二）开发商。开发商在旧城更新过程中，起到协调政府实施开发的作用，是具体工程项目的完成者。在得到政府的委托后，开发商一方面凭借自身强大的资金量，承担起拆迁和建设等任务，大大缓解了地方政府在更新过程中面临的资金压力，另一方面，因其自身完善的工作机制和丰富的工程实施经验，能较为独立的做好实施、管理、运营等多个环节的工作［4］。

（三）被拆迁者。居住在旧城的城市居民，当面临所居房屋要被拆迁时，经常会成为相对弱势的群体，因为如果对拆迁协议不满，只能通过上访或者述诸法律等方式维护自身的利益，但拆迁的政策是政府制定的，被拆迁者能为自己争取更多利益的机会就显得十分有限［5］。但是，如果在实际更新过程中，不注重保护被拆迁者的利益，很可能引起被拆迁人的强烈抗议，如果事情激化，被拆迁者甚至可能采取极端的行为，给更新的过程带来不小的阻挠。

二、博弈论方法的研究

（一）博弈论的概念

博弈论，也叫作对策论（Game Theory），是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题［6］，最早作为标准分析工具运用在经济学上，后来被广泛运用在国际关系、军事战略、应用数学、计算机科学、生物学等学科上。

博弈论是研究在博弈局中，各个博弈参与者根据自身利益和所了解的信息状况，不断预测对方的策略，从而更换自身的行为策略，来达到优化选择的目的。博弈论的核心在于博弈局中的任何一位理性决策者需要对其他理性决策者的行为策略做出分析和反应，从而作出最大限度保全自身利益的策略选择。我国古代的“田忌赛马”就体现出了博弈论的方法，田忌通过了解对方赛马的竞技水平，来调整己方赛马的出战顺序，获取胜利（表1）。

表1 田忌赛马战况表

（二）更新参与主体的博弈战略集

1.地方政府的行为选择

在旧城再开发模式更新下，地方政府是更新的主导者，同时另外一种身份是参与者，在这个更新博弈局中，地方政府有两种策略，分别是地方政府独立出资，自行开发和委托开发商来开发，这两种策略的选择，需要地方政府权衡自身的效益和财政能力［7］。如果地方政府选择自行开发这种策略，那么其首先将独立地承担开发的全部费用，支出将会很大，地方政府必须确保自身的财政能力大于这些费用，但如果开发能够顺利完成并达到不错的效果，更新所带来的各方面的收益都归属于地方政府；如果地方政府选择委托开发商来开发这种策略，那么开发的费用就由开发商来承担，地方政府为保证开发的顺利进行，往往会提供给开发商一些优惠的政策，同时对工程项目提供补贴。

2.开发商的行为选择

对于地方政府的委托，开发商有介入和不介入两种策略。作为总是把追求最大经济利益放在首位的集体或者个人，开发商的选择需要综合考虑期望效用的大小。对于是否介入旧城再开发的问题，开发商不仅仅会考虑如果介入是否能实现盈利以及能够盈利多少，还会与其他地块的土地开发项目作比较，以此来选择利润率最高的那个来介入。而对于旧城再开发涉及到的拆迁、补偿和安置等问题，开发商将会付出不菲的人力、物力和财力成本，所以，开发商需要得到政府在政策、税费和补贴等方面的大力支持［8］。

3.被拆迁者的行为选择

总的来说，被拆迁者有支持和不支持两种策略。无论是政府选择自行开发还是委托开发商开发，被拆迁者都可以选择支持或者不支持。被拆迁者是更新中较为弱势的群体，但是对于再开发所必需的拆迁腾地，被拆迁者如果选择不支持的策略，将可能会与其他参与者抗衡，拖延时间来争取自身利益，这样可能会延误工程项目的建设造成比较严重的损失，所以被拆迁者的态度直接影响了更新是否能够顺利进行。被拆迁者如何选择取决于其期望效用，如果期望效用远远大于0，旧城再开发就会得到被拆迁者的支持［9］。所以其他参与者需要保障被拆迁者的合理的利益诉求，才能确保更新顺利进行。

三、扩展式博弈模型的建立

从前文对旧城再开发模式下更新参与者利益问题的研究中可以看出，其博弈属于完全信息的动态博弈。在更新的博弈局中，地方政府先采取策略，开发商和被拆迁者随后相应的选择自己的策略。将P（Profit）作为各参与者的最终得益，用g（government）表示政府，d（developer）表示开发商，h（house owner）表示被拆迁者，建立扩展式博弈模型如下（图1）：

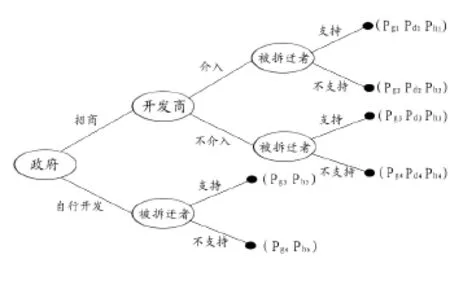
图1 扩展式博弈模型

由上图的扩展式博弈模型可见，由于更新参与者每一阶段都可能选择不同的策略，因此，博弈局中可以得到六种效用函数组合，用S表示策略，则六种效用函数组合如下：

四、博弈效用函数的分析

（一）地方政府的效用函数分析

在旧城更新博弈局中，地方政府最先选择策略，其策略集合是Sg=｛Sg1，Sg2｝，即｛自行开发，招商｝。假设地方政府的全部效用函数为T（g），C表示旧城更新所需要的开发成本，包括拆迁补偿和安置费用以及工程建设的成本；E表示地方政府提供给开发商优惠政策的成本；F表示地方政府为保障更新能够顺利进行，提供给开发商的补贴；J表示地方政府提供优惠政策和补贴后，开发商得到的收益；K表示地方政府不提供优惠政策和补贴时开发商获得的收益，k＜C＜J+E+F。地方政府的期望效用函数为Pg。

①当地方政府选择招商策略时，即Sg=Sg1，则Pg=T（g）+C-J-E-F或者Pg=T（g）+C-K

②当地方政府选择自行开发策略时，即Sg= Sg2，则Pg=T（g）-C

（二）开发商的效用函数分析

当地方政府选择采取招商策略后，开发商有介入和不介入两种策略，即策略集合Sd=｛Sd1，Sd2｝，Sd1表示介入，Sd2表示不介入。开发商的期望效用函数为Pd。

①当开发商选择介入时，即Sd=Sd1，则Pd= J-C+E+F或者则Pd=K-C

②当开发商选择不介入时，即Sd=Sd2，则Pd=C

（三）被拆迁者的效用函数分析

无论是地方政府自行开发还是地方政府委托开发商开发，被拆迁者都有支持和不支持两种策略，即策略集合Sh=｛Sh1，Sh2｝，Sh1表示支持，Sh2表示不支持。假设被拆迁者得到的补偿费用为M，安置得到利益为N，因为拆迁腾地遭受直接损失L，R表示被拆迁者面临未来生计的风险，系数为v（0＜v＜1）。被拆迁者的期望效用函数Ph。

①当被拆迁者选择支持时，即Sh=Sh1，则Ph= M+N-L-Rv

②当被拆迁者选择不支持时，即Sh=Sh2，则Ph=0

（四）博弈各阶段三方得益

（Pg5，Ph5）=（T（g）-C，M+N-L-Rv）；（Pg6，Ph6）=（T（g）-C，0）

地方政府采取自行开发策略的条件是，自行开发模式下地方政府的收益Pg5要大于招商模式下的地方政府收益Pg1，即T（g）-C＞T（g）+C-J-E-F，所以当C＜（J+E+F）／2时，地方政府会采取自行开发策略。

五、博弈模型的均衡结果

（一）地方政府与被拆迁者的均衡结果

地方政府和被拆迁者的博弈均衡解有两种（招商，自行开发）和（支持，不支持），但在现实情况下，地方政府作为更新的主导者将会动用一切社会资源来保障更新的顺利进行，因此最终被拆迁者都会选择支持，较为理想的情况是被拆迁者主动支持，则被拆迁者选择支持的收益M+N-L-Rv大于选择不支持的收益L+Rv，M+N-L-Rv＞L+Rv，M+N＞2L+2Rv（表2）。

表2 地方政府与被拆迁者的博弈矩阵表

（二）地方政府与开发商的均衡结果

如果地方政府不让利招商，自身得到最大的收益是T（g）+c-K，此时，对于开发商来说，接受这样的方案风险会很高，甚至有亏本的可能，开发商不会愿意轻易介入，地方政府最终会有一定程度的妥协，提供一定的优惠方案和补贴，实现双赢的局面，（T（g）+C-J-E-F，J-C+E+F）为“纳什均衡”解（表3）。

表3 地方政府与开发商的博弈矩阵表

（三）开发商与被拆迁者的均衡结果

“纳什均衡”解是开发商的介入和被拆迁者的支持，形成这种最优解需要满足两个条件，第一个是开发商介入的收益大于不介入的收益，即J-C+E+F＞C，C＜（J+E+F）／2；第二个是被拆迁者选择支持的收益大于选择不支持的收益，即M+N-L-Rv＞L+Rv，M+N＞2L+2Rv（表4）。

表4 开发商与被拆迁者的博弈矩阵表

六、结论

旧城更新是一个实践性较强的综合性问题，用博弈论的方法能够有效地将各利益主体的行为策略扩展出来，从而可以清晰地认识他们之间的矛盾点，在具体的实践中，如果能够将文中的子标最大精度地估算出来，进行一定程度的量化，实现M+N＞2L+2Rv，且C＜（J+E+F）／2时，地方政府、开发商和被拆迁者都能够最大限度的保障自身的利益，实现多方共赢。式中C表示旧城更新所需要的开发成本，包括拆迁补偿和安置费用以及工程建设的成本；E表示地方政府提供给开发商优惠政策的成本；F表示地方政府为保障更新能够顺利进行，提供给开发商的补贴；J表示地方政府提供优惠政策和补贴后，开发商得到的收益；K表示地方政府不提供优惠政策和补贴时开发商获得的收益，被拆迁者得到的补偿费用为M，安置得到利益为N，因为拆迁腾地遭受直接损失L，R表示被拆迁者面临未来生计的风险，系数为v（0＜v＜1）。

［1］杨俊宴.旧城规划设计［M］.辽宁:辽宁科学技术出版社, 2009（1）:2-3.

［2］李德华.城市规划原理［M］.北京:中国建筑工业出版社, 2001（3）:561.

［3］万勇.旧城的和谐更新［M］.北京:中国建筑工业出版社. 2006.

［4］廖乙勇.都市更新主体之共生模式—以台北市为例［M］.南京:东南大学出版社,2011.

［5］阳建强,吴明伟.现代城市更新［M］.南京:东南大学出版社,1999.

［6］张维迎.博弈论与信息经济学［M］.上海:上海人民出版社,1996（2）:36

［7］高曼.基于博弈论的城中村改造对策研究［D］.西安:西安建筑科技大学,2012.

［8］吕霁.基于博弈论的城中村改造模式研究［D］.武汉:华中师范大学,2008.

［9］张果果.贵州乡村旅游发展模式探索—基于博弈论的视角［D］.贵州:贵州大学,2008:4.

［10］陈煊.城市更新过程中地方政府、开发商、民众的角色关系研究［D］.武汉:华中科技大学,2009.

（责任编辑：戢斗勇jidouyong@qq.com）

The Interests Balance Problem Researching of the Old City Update Process Based on Game Theory

SHAOJian-jie
（Civil EngineeringSchool,Hubei Polytechnic University,Huangshi 435000,China）

Redevelopment of old city is in the process of our urban-rural integration,involving with many aspects of the society.The main participants of redevelopment of city include local government,developers and the demolished.Whether participation subject interests in the process of old city renewal is balancedwill directly decide whether the redevelopment can work smoothly.This paper applies the game theory,which the method of extended tripartite game model is set up,to analyze the behavior of the three parties’strategy,and by studying the game equilibrium to explore the method of realization of tripartite win-win results.

old city renewing;game theory;equilibrium balance

F293.22

A

1008-018X（2016）04-0019-04

2016-05-18

邵剑杰（1986-），男，湖北黄石人，湖北理工学院讲师。