一种确定火箭弹静不稳定度边界值的方法
方海红,庄 凌,董春杨,鞠晓燕,宋景亮
(北京航天长征飞行器研究所,北京,100076)
一种确定火箭弹静不稳定度边界值的方法
方海红,庄 凌,董春杨,鞠晓燕,宋景亮
(北京航天长征飞行器研究所,北京,100076)
放宽火箭弹的静稳定度在降低火箭弹成本,提高火箭弹射程、机动能力等性能的同时也给控制系统的稳定性带来影响,确定系统最大可适应的静稳定度对火箭弹总体设计技术具有重要意义。以过载反馈回路为基础提出一种确定静不稳定度边界值的方法,并通过仿真验证了其正确性,为工程研制早期阶段的总体设计以及控制系统的性能评估提供依据。
静不稳定度;火箭弹;控制系统稳定性
0 引 言
火箭弹作为常规火药在局部军事打击中发挥重要作用,其射程、机动能力、射击精度等是武器系统设计的重要因素。为满足纵深打击的需求,开展了远程制导火箭弹技术的研究以提高火箭弹的作战能力[1~3]。
研究表明,飞行器的稳定性、机动性均与静稳定度有关,静稳定度越大,飞行器的运动稳定性越好,但机动性越差;反之,静稳定度越小或者静不稳定,则运动稳定性越差,机动性越好。在飞行器速度和高度一定的情况下,飞行中所能产生的过载取决于攻角、侧滑角及舵面偏转角。由于飞行器在飞行过程中基本气动外形不变,所以随着静稳定度的降低,导弹可用过载增大,在飞行器处于静不稳定状态时质心更靠后,配平弹翼和弹身产生力矩的气动力减小,从而舵面面积和质量都将相应减小。因此,为了改善飞行器的机动性,飞行器弹体特性设计上不断朝着临界稳定或静不稳定特性方向发展,以空空导弹尤为显著[4]。
为了保证飞行稳定性,传统火箭弹均设计为静稳定特性,一方面限制了火箭弹的机动性能,另一方面为了实现火箭弹的静稳定需要为火箭弹增加配重,这无疑增加了火箭弹的重量,同时减小了火箭弹有效载荷,对火箭弹的射程以及作战效能带来影响。为了降低火箭弹成本,提高火箭弹射程、机动能力等性能,增加火箭弹单车作战情况下的打击覆盖范围,开展静不稳定设计技术是未来制导火箭弹的发展趋势。由于低成本的要求,这类火箭弹所选用的惯性测量装置、舵机组合的动态性能均受到一定限制,这对静不稳定火箭弹的设计带来挑战,确定系统最大可适应的静稳定度对火箭弹的总体设计技术具有重要意义。
本文以过载反馈回路为基础提出了一种分析静不稳定度边界值的确定方法,为工程研制早期阶段的总体设计以及控制系统的性能评估提供依据。
1 基础数学模型
为了进行火箭弹自动驾驶仪设计并对其稳定性进行分析,基于冻结系数法和小扰动线性化的假设,建立火箭弹的纵向运动模型。
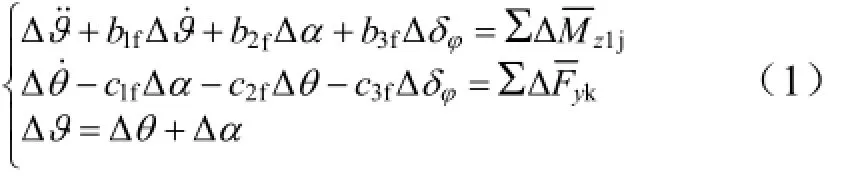
式中 Δϑ为俯仰姿态角偏差;Δθ为速度倾角偏差;Δα为攻角偏差;Δδφ为俯仰舵偏值;ΔMz1j为作用在俯仰方向上的干扰力矩;ΔFyk为作用在俯仰方向上的干扰力;b1f,b2f,b3f,c1f,c2f,c3f为俯仰方向弹体模型参数。
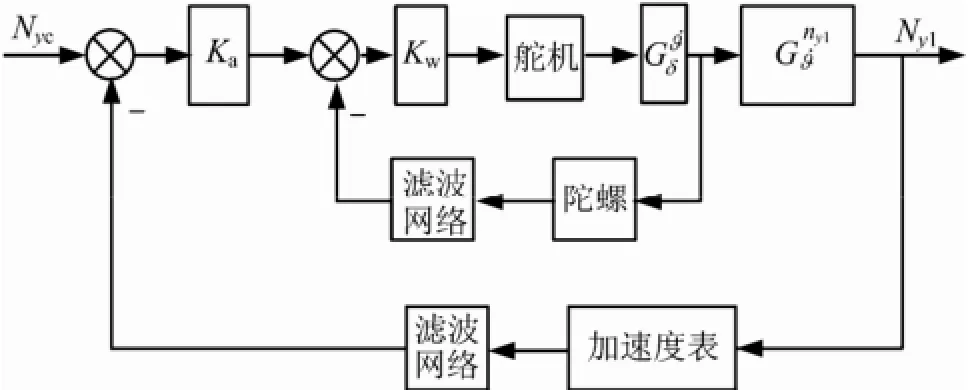
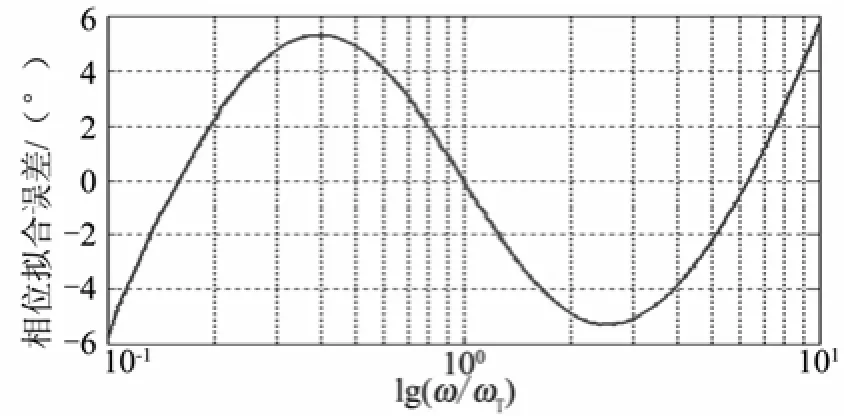
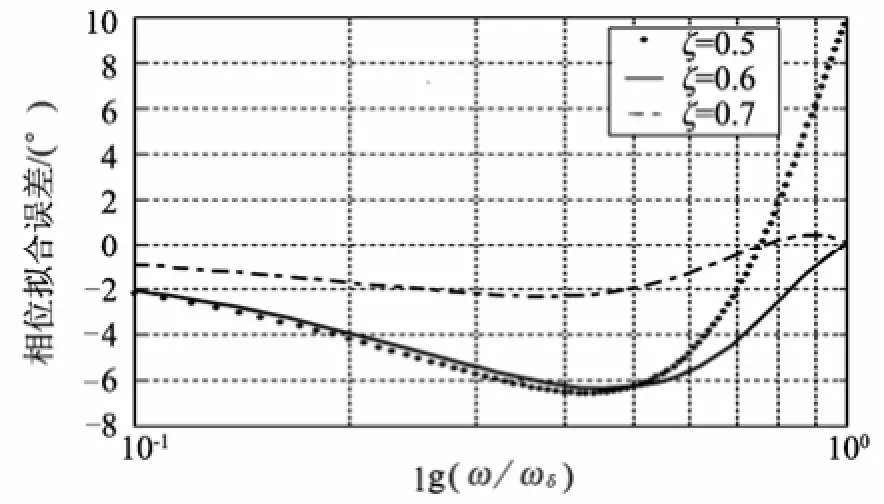
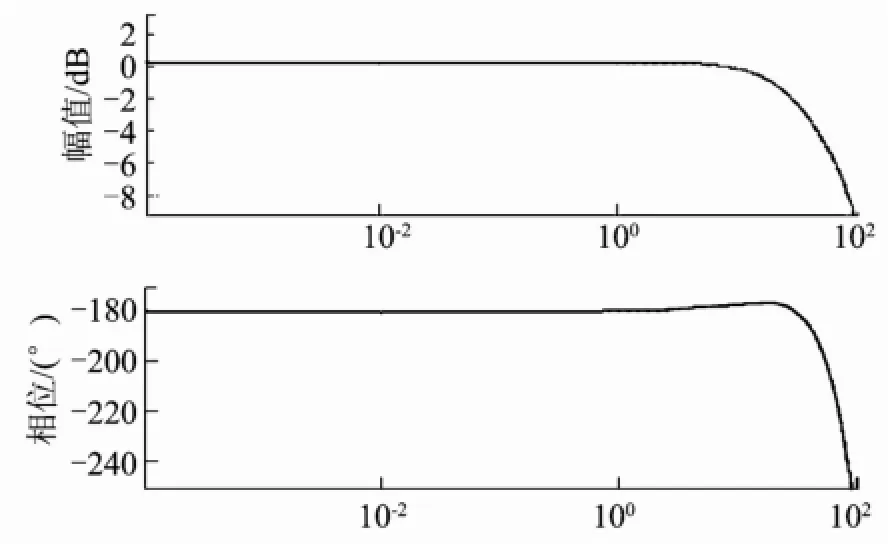
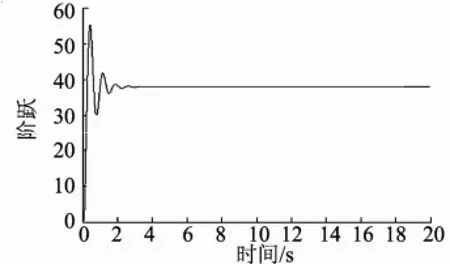
考虑火箭弹正常式布局,有c3f< 可得到过载传递函数: 根据文献[4],对于静不稳定飞行器可以通过人工增稳的方法实现稳定,且不同的自动驾驶仪回路结构对静不稳定度的适应程度不一致[5,6],而过载反馈回路结构对静不稳定具有更好的适应性。在本文中考虑选择如图1所示的过载反馈回路结构进行分析。舵机、陀螺以及加速度表采用传统的数学模型,具体如式(5)~(7)所示。 图1 两回路过载反馈自动驾驶仪结构形式 式中agc,,GGGδ分别为舵机、陀螺与加速度表的动态数学模型,与设备的特性有关;agc,,ςςςδ为阻尼比参数,一般为0.5~0.7;δωωω,,agc分别为陀螺、加速度表和舵机带宽;agc,ττ分别为陀螺和加速度表的延时。agc,ωω在几十赫兹时,对于MeMS陀螺及加速度表agc,ττ数值可达10 ms,δω范围较大。 根据图1可以写出系统的开环传递函数: 根据工程实际数据,加速度表的动态特性优于陀螺,因此分析中可取加速度表与陀螺的传递函数一致以简化分析过程,即Ga=Ggc,则系统开环传递函数为 为论述方便,将oG改写成: 式中 开环系统伯德图曲线如图2所示[7]。 图2 系统开环伯德图渐近曲线 从图2中可见:在KdB一定的情况下,随着的增大即静不稳定度的增加,ωT2向高频部分移动,从而ωc将向高频部分移动,整个开环系统的相角裕度γ以及幅值裕度Kg随之减小,到一定程度系统将出现不稳定的现象。 根据图2曲线,在其他参数不变时,若A2增大则系统带宽增加,系统的稳定裕度下降,A2的临界值为系统裕度达到零,同时系统静态增益对带宽也有贡献,当静态增益为0 dB时,增益达到最大。 根据系统的稳定性条件,系统稳定的极限条件须满足如下条件: 考虑到控制系统设计中舵机带宽ωδ远高于控制系统的带宽ωc,为了便于求解,在主值区间内可将相位角度方程中的第1项arctan(ω/ωT1)采用式(16)所示的线性方程近似代替,将方程中的第2项arctan((2ςω/ωδ)/(1-ω2/ωδ2))采用式(17)代替。 则,式(15)的第1式可以简化为 对于式(18)第1项产生的最小相位为45°,最大相位为90°,因此有: 从而,ωc满足如下: 根据式(15)在极限条件下有ωT1=A2/ωc,因此有下式成立: 应用式(20)、式(21)可得到允许的最大静不稳定。 图3、图4给出了替代方法下的相位拟合误差曲线。 图3 式(16)拟合误差曲线 图4 式(17)拟合误差曲线 将式(21)展开并整理可得: 令y=1+2logωc-Kωcωc,其中Kωc=80/(45ωδ)+4/(π)·τgc,将y对ωc求导数: 应用极值原理[8],ωc=2ln·(1/Kωc)时,y取到极大值。 由于2ln·(1/Kωc)=0.868/Kωc<1/Kωc,因此当ωc=1/Kωc时,取最大值且最大值满足: 从而可得到采用以过载+角速度反馈回路结构进行静不稳定弹体特性稳定控制时,系统能够适应的最大静不稳定度: 根据结果,系统可适应的最大静不稳定度由舵机带宽以及陀螺的延迟时间决定。 给定ωδ=18 Hz,τgc=0.01,计算可得到=1 235,ωc=35.1 rad/s。 假定系统参数为 选取自动驾驶仪的控制参数为:Kw=0.139,Ka=0.543。仿真得到系统的伯德图如图5所示,阶跃响应曲线如图6所示。调整A2=-1 200在参数不变情况下的阶跃响应曲线如图7所示。 图5 静不稳定取极值时伯德图 图6 静不稳定取极值时阶跃响应 图7 静不稳定降低(A2=-1 200)后阶跃响应 根据仿真结果可以看出:在式(25)所确定的静不稳定度条件下系统为不稳定状态,将静不稳定度缩小1%之后系统稳定,表明式(25)的结果正确。 本文以纵向通道为例对静不稳定火箭弹静不稳定边界值进行了研究,给出了过载反馈自动驾驶仪的结构,并且推导给出了该自动驾驶仪结构下控制系统的开环传递函数,给出了其伯德图,分析了静不稳定度对系统稳定性的影响,基于系统的稳定条件推导了系统可适应的最大静不稳定的极值点及其具体计算公式。本文结果以火箭弹为基础推导得到,但同样可以适用于其他飞行器,为工程研制早期阶段的总体设计以及控制系统的性能评估提供依据。 [1] 岳松堂. 多管火箭炮及其远程制导弹药[J]. 现代军事, 2007(2): 26-31. [2] 轶名. WS-2多管远程制导火箭系统[J]. 现代军事, 2007(2): 34-35. [3] 陈光文. 解析我国最新型“神鹰”400制导火箭炮系统[J]. 现代兵器, 2009(2): 22-26. [4] 关世义. 放宽静稳定性原理在现代飞行器设计中的应用[J]. 战术导弹技术, 1985(2). [5] 程云龙. 防空导弹自动驾驶仪设计[M]. 北京: 中国宇航出版社, 2007. [6] 刘代军. 自动驾驶仪结构对静不稳定弹体的适应性分析[J]. 战术导弹技术, 2001(3): 47-53. [7] 李友善. 自动控制原理[M]. 北京: 国防工业出版社, 1989. [8] 关肇值, 韩京清. 极值控制与极大值原理[M]. 北京: 科学出版社, 1980. A Method to Calculate the Static degree of Unstable Boundary of Guided-Rocket Fang Hai-hong, Zhuang Ling, dong chun-yang, Ju Xiao-yan, Song Jing-liang enhancing the static degree of stability is useful for reducing the cost, improving the maneuver and range capability of the rocket and also effecting the stability of the control system. confirming the maximum unstable stability is significant for the design of guided-rocket. a method to calculate the static degree of unstable boundary is proposed based on the overloading feedback loop and be demonstrated through simulation which supplies evidence for general design in early research stage and performance evaluation of control system. Static degree of unstable; Rocket; control system stability V414.3+4 a 1004-7182(2016)01-0077-04 10.7654/j.issn.1004-7182.20160118 2015-03-23; 2015-06-12 方海红(1979-),男,高级工程师,主要研究方向为飞行器导航、制导与控制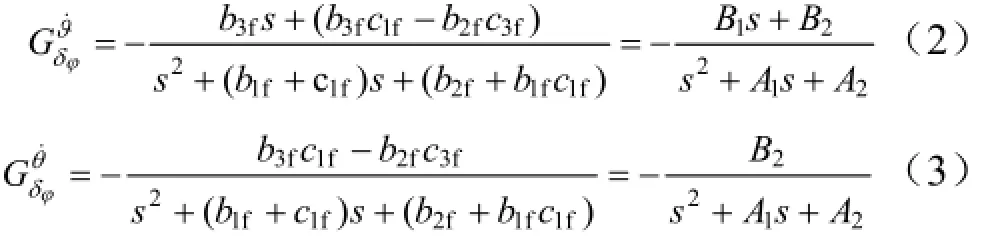
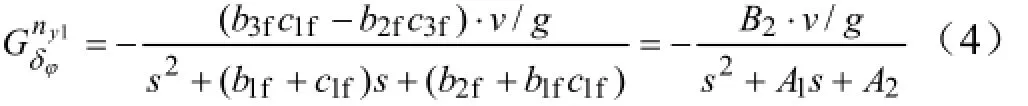
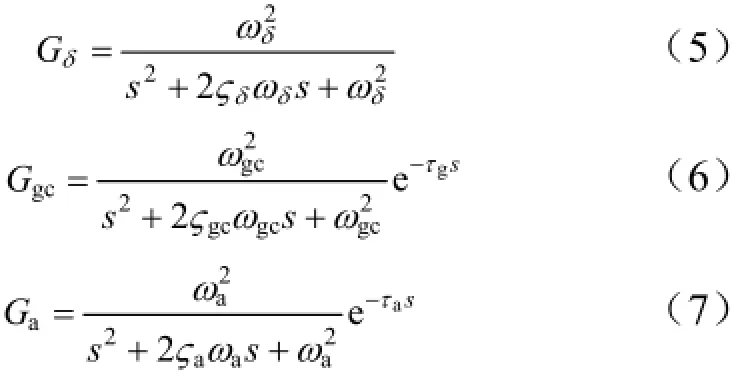
2 静不稳定度对稳定性影响分析
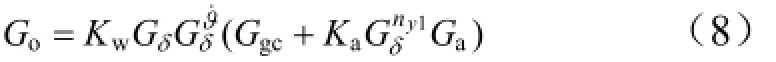
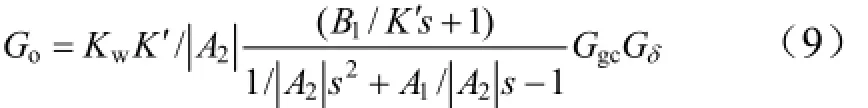

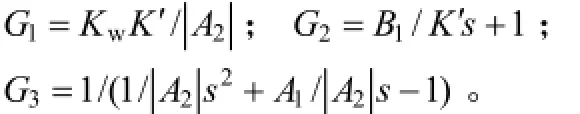
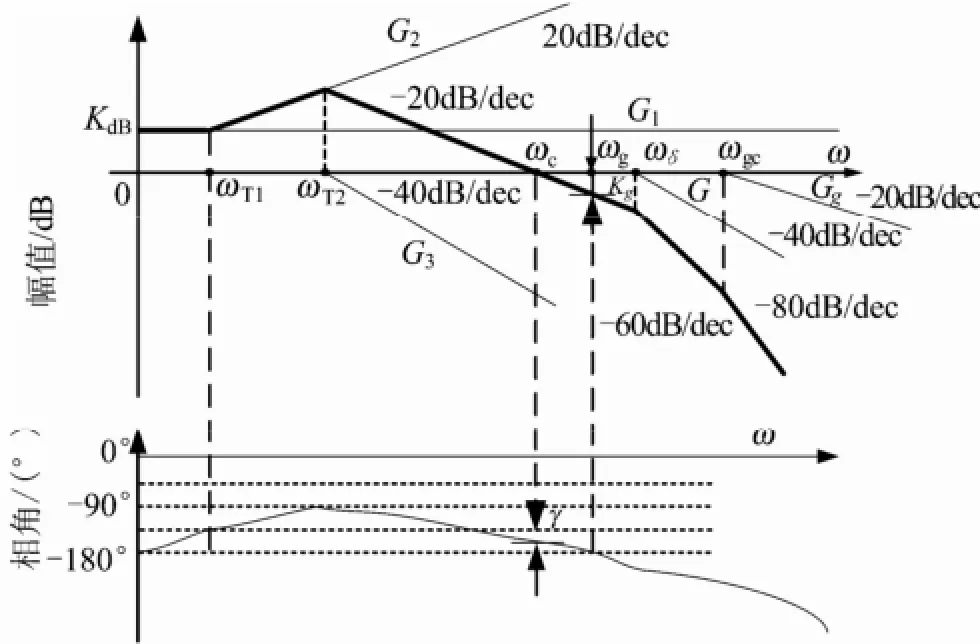


3 静不稳定边界值分析
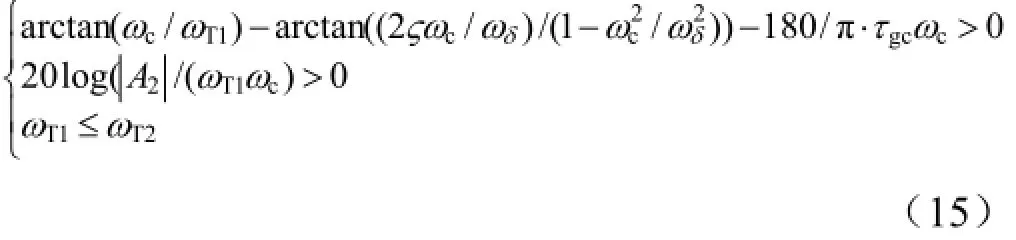
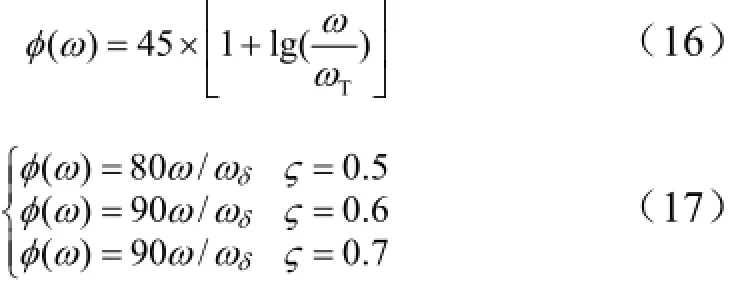
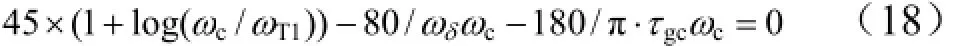
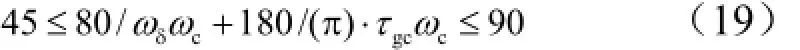
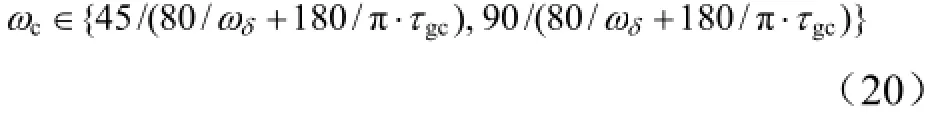
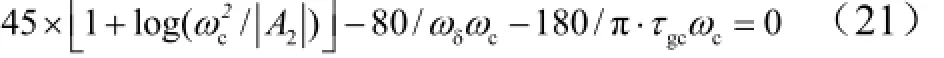

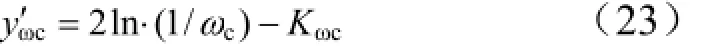
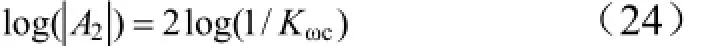
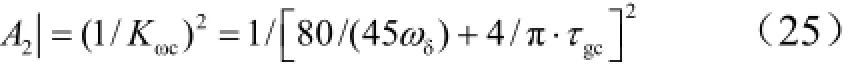


4 结 论
(Beijing Institute of Space Long March Vehicle, Beijing, 100076)

