orbifold丛的群胚表示

林奕武（广东金融学院应用数学系，广东广州510275）



orbifold丛的群胚表示

林奕武
（广东金融学院应用数学系，广东广州510275）

摘要：该文定义了orbifold丛的群胚表示，并且用群胚的语言重新定义orbifold的de Rham上同调和K-理论。

关键词：orbifold丛；群胚；群胚K-理论；丛映射

众所周知，orbifold理论涉及数学的众多分支，如拓扑学，代数几何与弦理论等。上世纪50年代，Satake［1，2］首次在拓扑与微分几何领域中引进orbifold的概念。他视orbifold为光滑流形的推广，并称之为V-流形。传统上，orbifold被视为带有奇点的“流形”，如在代数几何常称orbifold为带商奇性的簇，即将or⁃bifold奇性视为拓扑空间的内蕴结构。在拓扑中，常常将orbifold奇性视为拓扑流形上的一个orbifold结构，类似于拓扑流形的光滑结构。但是，由于orbi⁃fold的奇性结构，使得光滑流形上的很多概念无法推广到orbifold范畴。因此，Haefliger［3］和Moerdijk［4，5］等人为orbifold引入了群胚的语言。Moerdijk指出，每个orbifold都对应着一个李群胚，使得orbifold底空间刚好李群胚的轨道空间。orbifold的局部奇性结构可以从李群胚的态空间得到。因此用群胚的语言来表述orbifold是具有积极意义的。首先，可以构造李群胚的分类空间，使得基本群，de Rham上同调等几何的不变量可以在orbifold上发展起来。另外，Adem、Lei⁃da和Ruan［6］在李群胚上构造了纤维丛。而Chen和Ruan［7］在研究orbifold的弦理论的过程中发现了orbi⁃fold上同调，引起了广泛的关注。

笔者在Adem、Leida和Ruan［6］的基础上，首先，把orbifold的切丛，余切丛和外形式丛等定义成or⁃bifold上的一个群胚。把外微分形式，即从orbifold到外形式丛的截面，视为一个群胚同态。因此用新的群胚语言对de Rham上同调重新描述，使其定义更加自然。接着，本文把orbifold的纤维丛定义成一个群胚，把丛同态定义为群胚之间的同态，从而定义了orbifold群胚上的群胚K-理论，并且证明这种定义在Morita等价下是不变的，因此可以作为orbi⁃fold的K-理论。

一、orbifold及orbifold群胚

本节主要介绍orbifold，orbifold丛及orbifold群胚等概念，这些概念主要来自于［6］。

orbifold可以用两种语言来描述，一种是局部卡的语言，另一种是群胚的语言。orbifold的局部卡类似于流形的局部坐标卡，一个orbifold可视为赋予了局部卡册的Hausdorff拓扑空间。用局部卡的语言，我们能直观的看到orbifold的局部结构。orbifold也可以视为李群胚的轨道空间。用群胚的语言，我们能把群胚的丰富技巧移植到orbifold理论，从而基本群，上同调等拓扑不变量可以推广到orbifold范畴。

定义1.1设X为一个仿紧的Hausdorff拓扑空间，n≥0。

（4）X的两个orbifold卡册ℑ和ℵ，如果ℑ中的每一张orbifold卡都能嵌入ℵ中的某一张orbifold卡，则称ℑ为ℵ的一个加细。如果两个orbifold卡册有一个共同的加细，则称它们是等价的。

一个群胚是指一个小范畴，其所有态射都是等价。一个李群胚是指一个具有光滑结构的群胚，定义如下：

（1）源映射s:G1→G0为淹没映射；

（2）靶映射t:G1→G0为淹没映射；

（3）复合映射m:G1s×tG1→G1满足结合律，

其中G1s×tG1={(h,g)∈G1×G1|s(h)=t(g)};

（4）单位映射u:G0→G1，x↦1x；

（5）逆映射i:G1→G1，g↦g-1.

定义1.3设G=(G0,G1)为李群胚，如果(s,t):G1→G0×G0为固有映射，并且s,t都是局部微分同胚，则称G=(G0,G1)为一个orbifold群胚。

设G为orbifold群胚。对于任意x∈G0,存在自然的群同态

ρx: Gx→diff（Ux）,

其中，Ux为x的开邻域，Gx={g∈G1|s(g)=t(g)=x} 为x的局部子群。若对于所有x∈G0，ρx:Gx→diff(Ux)都为单态，则称G为有效的orbifold群胚。否则，称为非有效的orbifold群胚。

例1.4每个有限李群G可以看作一个orbifold群胚。其象空间为一个单点，态空间为G .我们称之为点群胚，记为G.

例1.5每个光滑流形M也可以看作一个orbi⁃fold群胚。其象空间和态空间都是M，所有的结构映射都是恒同id: M→M.由于每个态射都是单位态，我们称之为单位群胚。

接着讨论orbifold群胚之间的同态与等价，我们可以利用orbifold群胚之间等价给所有orbifold群胚分类。

二、orbifold切丛及orbifold de Rham上同调

考虑G1上的切丛TG1，首先证明TG1与G1×G0TG0是同构的。

对于拉回图表（见图1）：

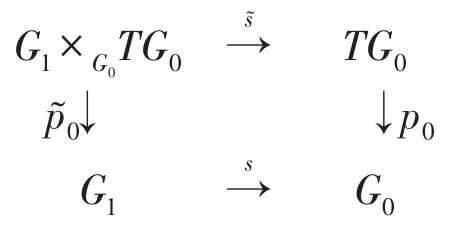
因为存在切映射s∗:TG1→TG0和p1:TG1→G1，使得p0s∗=sp1.因此存在

Ψ:TG1→G1×G0TG0

定理2.1 (TG0, TG1)是一个orbifold群胚，并且

(1TG0,Ψ): (TG0,TG1)→(TG0,G1×G0TG1)是orbifold群胚同构。

定义2.2我们称(TG0,TG1)为=(G0,G1)的切丛。

同理，我们定义(T∗G0,T∗G1)为=(G0,G1)的余切丛。定义为G=(G0,G1)的r次外形式丛，记为.

Adem、Leida和Ruan［6］把G的de Rham复形

接着我们证明这两种de Rham复形的定义是一致的。

又因为ϕdω=(dω,s∗dω)=(dω,ds∗ω)=dϕω。所以ϕ是链复形同构。

三、群胚丛及群胚K-理论

本节，我们用群胚的语言来定义orbifold丛和orbifold K-理论。

使得p0:E0→G0和p1:E1→G1都是丛投射，则称上的一个群胚丛。上群胚丛(F0,F1)和(E0,E1)之间的群胚丛映射定义为满足丛映射条件的群胚同态，即是

其中(ρ0,ρ1)为群胚同态，并且ρ0:F0→E0和ρ1:F1→E1都是丛映射。

如果(ρ0,ρ1)是同构映射对，则称(F0,F1)和(E0,E1)是同构的群胚丛。

设(f0,f1):(G0,G1)→(H0,H1)是群胚同态，(E0,E1) 是(H0,H1)上的群胚丛，则f0和f1的拉回和是(G0,G1)上的一对纤维丛。

证明：考虑下面图表：

图2　交换图

推论3.4 (f0,f1)诱导了一个群胚K-理论的同态

特别地，

定理3.5 (f0,f1)是一个Morita等价，则

因为Morita等价的orbifold群胚表示相同的or⁃bifold，所以群胚K-理论可以视为orbifold上的K-理论。

参考文献

［1］I Satake. On a generalization of the notion of manifold ［J］. Proceedings of the National Academy of Science of the United States of America，1956，42（6）：359-363.

［2］I Satake. The Gauss-Bonnet theorem of V-manifold［J］. Mathematical Society of Japan，1957，9（4）：464-492.

［3］Haefliger Groupoids and folations in analysis［J］. Geome⁃try and physics，2001，28（2）：83-100.

［4］I. Moerdijk，I. Moerdijk. Orbifolds as groupoids：an In⁃trodution［J］. Orbifolds in mathematics and physics，2002，3（10）：205-222.

［5］I. Moerdijk，A. Dorette. Orbifolds，sheaves and Grou⁃poids［J］. K-Theory，1997（12）：3-21.

［6］A. Adem，J. Leida and Y. Ruan. Orbifolds and stringy to⁃pology［M］. Cambridge Tracts in Mathematics，2007.

［7］W. Chen，Y. Ruan. A new cohomology theory of orbifold ［J］. Comm. Math. Phy，2004，24（8）：1-31.

［经济与管理］

［经济与管理］

Groupoid Representation of Orbifold Bundles

LIN Yi-wu
（Department of Applied Mathematics，Guangdong University of Finance，Guangzhou 510521，China）

Abstrast：We define the groupoid representation of orbifold bundles，and describe the de Rham cohomology of orbifold using groupoid language，then define the groupoid K-theory on orbifolds.

Key words：orbifold bundle；groupoid；groupoid K-theory；bundle map

中图分类号：O189.2

文献标志码：A

文章编号：1009-931X（2016）01—0063-03

收稿日期：2015-12-10

基金项目：国家自然科学基金项目（11201087）

作者简介：林奕武（1980-），男，广东汕头人，博士，讲师，研究方向：orbifold及陈-阮上同调。