围岩侧向压力对隧道稳定性的影响研究

余灿鑫，王增立

(中铁十八局集团第二工程有限公司， 河北 唐山　063030)



围岩侧向压力对隧道稳定性的影响研究

余灿鑫，王增立

(中铁十八局集团第二工程有限公司， 河北 唐山063030)

摘要：围岩侧压力是否对隧道稳定性产生影响，不同的理论有不同结论。轴比论观点认为，洞室形状一定时，竖向压力和水平方向的围岩压力比值和隧道洞室的稳定性密切相关。然而，有限元强度折减法计算结果则表明，泊松比(对应不同侧压力系数)与隧道的安全系数大小无关。显然，这一结论与轴比论不符，也与实际不符。以某扁平隧道作为算例，采用改进的强度折减法计算不同泊松比对应的破坏形态及安全系数，计算结果表明：泊松比对隧道的破坏形态及安全性有影响，侧压力越大，则越容易发生边墙破坏；侧向压力越小，则越容易发生拱部破坏。

关键词：隧道；稳定性；强度折减法；泊松比

1问题提出

上世纪80年代，于学馥等[1]提出了轴比论。该理论有如下一些比较重要的结论。

1) 当a/b=λ=υ/(1-υ)时，隧道为受力的最优轴比，整个隧道围岩周围压应力均匀分布，不出现拉应力，出现的最大应力值最小。式中：a、b分别为椭圆隧道的短半轴和长半轴；λ为侧压力系数；υ为土体泊松比。某隧道椭圆形洞室受力示意如图1所示。

2) 当a/b=2λ/(1-λ)=2υ/(1-2υ)时，在边墙产生零应力，整个隧道仍不产生拉应力。

注：qx为水平方向侧压力，qz为竖向侧压力系数，θ为极角，r0为极径。

随着计算力学的发展，自上世纪70年代起，采用有限元强度折减法计算隧道安全系数的技术方法不断兴起，这种方法最初用于边坡稳定性计算，由于其与理论解非常吻合，故逐步得到认可。随后这种方法被应用于隧道安全系数计算探讨，并取得了一些有益结论。采用强度折减法计算时，考虑了岩土材料参数c(粘聚力)、tanφ(摩擦角的正切值)的折减，使其不断折减，直到有限元计算模型进入极限状态为止，通过这种方式来获取材料的安全储备大小。

然而，采用强度折减法计算隧道安全系数目前尚不成熟，计算时只考虑了材料强度参数折减对隧道稳定性的影响。张黎明等[2]对泊松比对隧道稳定性的影响进行了研究，研究结果表明，泊松比对隧道的稳定性不会造成影响。显然，不同泊松比υ会造成隧道侧压力系数不同，在相同竖向压力下，不同侧压力系数必将导致隧道稳定性不同。可见，强度折减法计算结果与轴比论不符，也与实际情况不符，因此有必要对有限元强度折减法中泊松比对隧道稳定性的影响进行研究。

2强度折减法改进

有限元计算分析中，选用不同折减系数按照式(1)不断地改变材料的强度参数，并将其带入有限元模型中进行试算。通过多次试算就能够找到“濒临破坏的极限状态”，该状态时的折减系数即为安全系数[3-6]。

(1)

式中：c′为强度折减后的粘聚力；φ′为强度折减后的摩擦角；F为折减系数。

采用有限元强度折减法计算隧道安全系数时，失效判据的选取非常重要。但长期以来，对有限元强度折减过程中失效判据的争议不断，而失效判据不同，将直接影响隧道安全系数的取值。目前学术界对有限元计算判据的争议非常激烈，以致2009年出现2篇观点相悖的论文同时被评为2009年中国百篇最具影响国内学术论文的现象[7-8]。

2012年，陈力华、靳晓光[9]针对这一争议问题进行了研究。其研究结果指出：1) 抗拉强度对隧道的稳定性是有影响的，在计算中应考虑；2) 强度折减法以计算的收敛性作为失效判据是合理的；3) 以往强度折减法对抗拉强度的高估是造成不同判据计算产生偏差的重要原因。

针对以往强度折减法存在的问题，文献[9]提出了改进的强度折减法。即为使强度折减后，材料抗剪强度安全储备大小及抗拉强度安全储备大小都能得到同等降低，须满足抗拉强度指标(T)与抗剪强度指标(c，tanφ)按照同一指标折减的要求：

(2)

3算例

为了研究不同泊松比是否对隧道稳定性产生影响，建立了如图2所示的有限元计算模型。模型长宽均为143 m。隧道为宽24 m、高16 m的椭圆形。隧道材料为服从摩尔-库仑屈服准则与非关联流动法则的理想弹塑性材料，材料重度γ=20 kN/m3，粘聚力c=200 kPa，内摩擦角φ=27°，剪切模量G=2 GPa，抗拉强度为20 kPa，泊松比υ取0.275～0.45。

图2　扁平椭圆隧道有限元计算模型

本文提出了不同泊松比极限状态时的塑性区云图，如图3所示。其中，深色区域表示“受拉塑性区”、浅色区域表示“受剪塑性区”。

图3　不同泊松比极限状态时扁平隧道的破坏模式

从图3可以看出，不同泊松比对应着不同的安全系数，随着泊松比增加(侧向压力增加)，整个洞室的稳定性呈先增加后减少趋势，这与轴比论的观点有一定的相关性和一致性。

当泊松比为0.275时，隧道在拱顶部位产生了“受拉塑性区”，说明隧道的稳定性受抗拉强度影响，首先在拱部产生张拉破坏(此时安全系数为0.82)；当泊松比为0.30时，隧道破坏类型有所转变，拱顶仍存在“受拉塑性区”，而拱腰新增了“受剪塑性区”，此时隧道的稳定性主要受抗拉强度和抗剪强度共同控制(此时安全系数为1.18)；当泊松比为0.325时，拱顶“受拉塑性区”消失，侧墙部位“受剪塑性区”范围进一步扩大，两腰局部产生了“受拉塑性区”，此时隧道的稳定性受抗剪强度控制(此时安全系数为1.62)；当泊松比为0.35～0.43时，“受剪塑性区”范围进一步扩大，两腰同时产生了一定范围的“受拉塑性区”(安全系数从1.82增至2.19，达到最大)，泊松比进一步增加，两腰处的“受拉塑性区”面积继续增加，安全系数骤减。 泊松比与安全系数的关系曲线如图4所示。

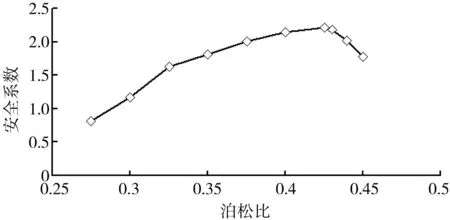
图4　扁平隧道不同泊松比安全系数

通过研究不同泊松比情况下隧道塑性区范围的变化及安全系数的变化规律，得到以下结论。

1) 隧道的稳定性与与泊松比密切相关，有限元强度折减法计算中必须考虑泊松比的影响。

2) 由于不同泊松比对应不同的侧压力系数，因此出现了最初的受拉塑性区从拱部向边墙转移的情况，即侧向压力越大，则越容易发生边墙破坏；侧向压力越小，则越容易发生拱部的破坏。

3) 以往强度折减法未考虑抗拉强度的折减，可能是导致计算结果与轴比论不符的原因。

4) 图2计算模型为扁平隧道，计算结论并不严格符合理论解，其中根本原因是实际围岩压力并不严格符合图1的理想情况。

4工程实例

由于长期以来对隧道稳定性没有一个量化的描述指标，隧道施工优或者不优，很多时候需凭借经验来确定，故即使采用有限元计算，局部受力大也并不意味着隧道整体就危险。强度折减法的引入，使隧道施工优或者不优能够被量化。下面通过1个算例，就某黄土隧道CRD法进洞应“左右开挖”还是“上下开挖”进行研究。

4.1施工工序比选

CRD法施工工艺如图5所示。现场采用的施工方法通常为“左右开挖”或“上下开挖”。

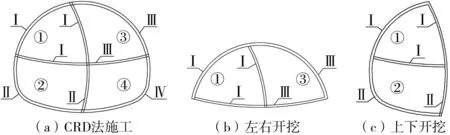
图5　CRD法施工工艺

左右开挖：开挖①→初期支护Ⅰ，中隔壁Ⅰ，临时仰拱Ⅰ→开挖③→初期支护Ⅲ，临时仰拱Ⅲ→开挖②→初期支护Ⅱ，中隔壁Ⅱ→开挖④→初期支护Ⅳ→拆除临时支撑→完成。

上下开挖：开挖①→初期支护Ⅰ，中隔壁Ⅰ，临时仰拱Ⅰ→开挖②→初期支护Ⅱ，中隔壁Ⅱ→开挖③→初期支护Ⅲ，临时仰拱Ⅲ→开挖④→初期支护Ⅳ→拆除临时支撑→完成。

为了施工方便，现场施工常常采用“左右开挖”方式，但这种方式是不是最优的开挖方式，似乎值得商榷探讨。

4.2有限元计算模型

有限元计算模型如图6所示。模型宽60 m，高30 m，隧道埋设10 m。“左右开挖”为上台阶开挖完成支护时的状况，“上下开挖”为左侧壁导坑开挖完成的状况。

图6　有限元计算模型

围岩和初期支护的物理力学参数如表1所示。初期支护及黄土的支护参数主要参照JTG D70—2004《公路隧道设计规范》[10]及GB 50010—2010《混凝土结构设计规范》[11]的参数确定。

4.3计算结果及分析

针对图6模型，采用强度折减法计算2个模型在极限状态时的状况。本文计算不仅考虑了抗剪强度指标的折减，而且还考虑了抗拉强度指标的折减。计算完毕后，提出隧道在2种开挖方式极限状态下的位移云图及塑性区云图，如图7～10所示。

表1　围岩和支护结构物理力学参数

注：E为弹性模量。

图7　“左右开挖”濒临破坏时竖向位移云图

图8　“左右开挖”破坏模式(F=2.48)

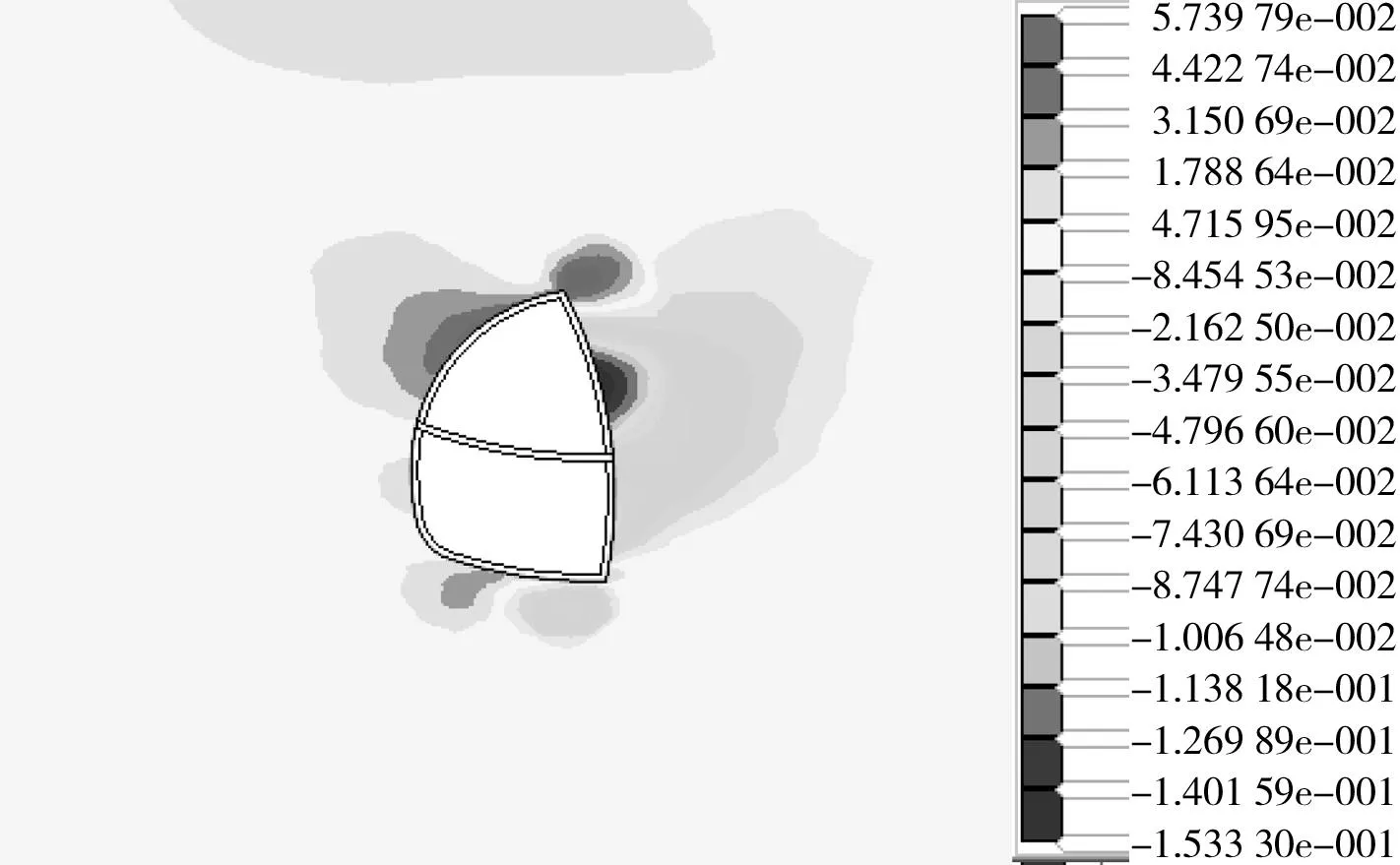
图9　“上下开挖”濒临破坏时水平位移云图

图10　“上下开挖”破坏模式(F=3.23)

对比图8和图10可以发现：

1) 对于“左右开挖”的隧道，其失稳方式为拱部坍塌，隧道产生了贯通于地表的塑性区，濒临破坏时，隧道安全系数为2.48；对于“上下开挖”的隧道，其破坏模式为边墙失稳，濒临破坏时，隧道安全系数为3.23。显然，按照“上下开挖”方式施工，施工过程中隧道更容易稳定。

2) 通常，隧道竖向围岩压力大于水平向的围岩压力，按“上下开挖”模式，施工过程中隧道的状态为最接近最优轴比的状态；而“左右开挖”模式产生的隧道为扁平结构，是极不利的断面形式，施工过程中应尽量避免。也许在某些较为稳定的地层中按照“左右开挖”方式施工也是可行的，但不是最优的。如果遇到软弱富水地层，隧道进洞比较困难时，CRD法施工应按照“上下开挖”方式进行。

3) 如果土体越差，泊松比就越接近0.5，侧向压力就越大，按照图5(c)开挖的侧壁就可能出现侧壁失稳的状况。此时采用横向支撑(临时仰拱)进行支护是有必要的，这也是CD法和CRD法在实际使用过程中的区别。

将以上黄土隧道模型泊松比调整为0.1并带入计算，得到“左右开挖”临界失效时的折减系数为2.50，“上下开挖”临界失效的折减系数为3.12。可见，若黄土隧道泊松比取0.1，则“左右开挖”时隧道安全系数变化不大。究其原因，可能是因为隧道的失稳形态为拱部失稳，主要受拱顶围岩荷载的控制所致。另外，改变泊松比对“上下开挖”时隧道稳定系数有较大影响。对于“上下开挖”的隧道，其失稳方式主要受侧向压力控制。2种泊松比临界失稳时，隧道横向支撑水平方向上的应力云图如图11所示。从图11中可以看出，υ=0.4对应的最大水平压应力为172 kPa，而υ=0.1对应的最大水平压应力为89 kPa。可见，泊松比越小，周围土体侧压力对横撑的作用力也越小。

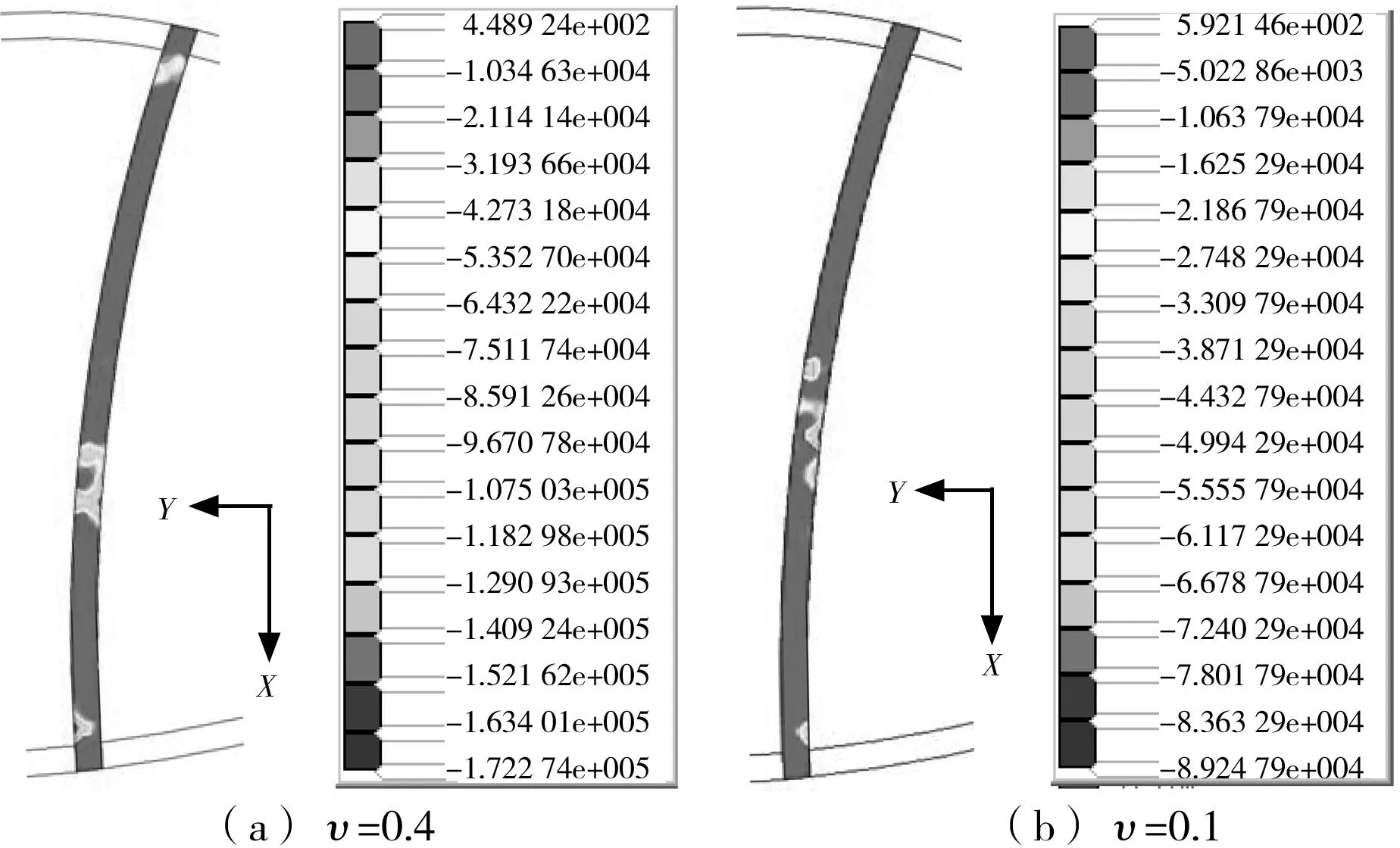
图11　水平方向应力云图(X为水平方向，Y为竖直方向)

5结论

1) 研究表明，泊松比对隧道安全系数计算有一定影响。

2) 有限元强度折减法计算时，必须考虑泊松比的影响，尤其是以侧墙失稳作为控制的隧道模型。

3) “上下开挖”施工方法是较为合理的施工方法，在围岩地质条件比较差的情况下应考虑采用这种开挖方式。

参 考 文 献

[1]于学馥，乔端．轴变论与围岩轴比三规律[J].有色金属，1981，33(3):8-14．

[2]张黎明，郑颖人，王在泉，等．有限元强度折减法在公路隧道中的应用探讨[J]．岩土力学，2007，28(1)：97-101．

[3]赵尚毅，郑颖人，时卫民，等．用有限元强度折减法求边坡稳定安全系数[J]．岩土工程学报，2002，24(3)：343-346．

[4]赵尚毅，郑颖人，邓卫东．用有限元强度折减法进行节理岩质边坡稳定性分析[J]．岩石力学与工程学报，2003， 22(2)：254-260．

[5]郑颖人，赵尚毅．有限元强度折减法在土坡与岩坡中的应用[J]．岩石力学与工程学报，2004，23(19)：381-388．

[6]UGAI K．A method of calculation of total safety factor of slopes by elastoplastic FEM [J]．Soils and Foundations，1989，29(2)：190-195．

[7]赵尚毅，郑颖人，张玉芳．极限分析有限元法讲座——II有限元强度折减法中边坡失稳的判据探讨[J]．岩土力学，2005，26(2)：332-336．

[8]刘金龙，栾茂田，赵少飞，等．关于强度折减有限元方法中边坡失稳判据的讨论[J]．岩土力学，2005，26(8)：1345-1348．

[9]陈力华，靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J]．土木工程学报，2012，45(9)：136-146．

[10]重庆交通科研设计院.JTG D70—2004公路隧道设计规范[S].北京：人民交通出版社，2004．

[11]中华人民共和国住房和城乡建设部，中华人民共和国国家质量监督检验检疫总局.GB 50010—2010混凝土结构设计规范[S]．北京:人民交通出版社，2010．

Research on Influences of Side Pressure of Wall Rocks on Stability of Tunnels

YU Canxin, WANG Zengli

Abstract:For influences of the side pressure of wall rocks on stability of tunnels, different theories draw different conclusions. In the viewpoint of the axial ratio theory, when the shape of caverns is fixed, the ratio of vertical pressure to the pressure on wall rocks in horizontal direction is closely related to stability of tunnel caverns. However, the calculation results of the finite element shear strength reduction method show that the Poisson's ratio (corresponding to different side pressure coefficients) is irrelevant to the safety factors of tunnels. Obviously this conclusion is inconsistent with the axial ratio theory and practicality. With some flat tunnel as an example, this paper adopts the modified strength reduction method to calculate failure modes and safety factors corresponding to different Poisson's ratios, and the calculation results show that the Poisson's ratio affects failure modes and safety of tunnels, the higher the side pressure, the easier the failure of side wall occurs; the lower the side pressure, the easier the failure of arc occurs.

Keywords:tunnel; stability; strength reduction method; Poisson's ratio

文章编号：1009-6477(2016)02-0093-05

中图分类号：U452.1+2

文献标识码：A

作者简介：余灿鑫(1984-)，男，四川省绵阳市人，本科，工程师。

收稿日期：2015-10-19

DOI:10.13607/j.cnki.gljt.2016.02.021