河网线要素与DEM综合的三维Douglas-Peucker算法

窦世卿，赵学胜，刘成军，林亚文，赵艳芹

1. 中国矿业大学(北京)地球科学与测绘工程学院，北京100083； 2. 黑龙江科技大学矿业工程学院，黑龙江 哈尔滨 150022； 3. 北京地林伟业信息技术有限责任公司，北京 100036； 4. 黑龙江科技大学计算机与信息工程学院，黑龙江 哈尔滨 150022



河网线要素与DEM综合的三维Douglas-Peucker算法

窦世卿1,2，赵学胜1，刘成军2，林亚文3，赵艳芹4

1. 中国矿业大学(北京)地球科学与测绘工程学院，北京100083； 2. 黑龙江科技大学矿业工程学院，黑龙江 哈尔滨 150022； 3. 北京地林伟业信息技术有限责任公司，北京 100036； 4. 黑龙江科技大学计算机与信息工程学院，黑龙江 哈尔滨 150022

摘要：目前三维Douglas-Peucker(3D_DP)算法主要应用于单一类型的DEM综合。本文引入“弯曲调节指数”来改进3D_DP算法，提出了一种三维空间河网要素与DEM综合的新方法，即将河网线矢量提取成三维离散点数据集(增加高程属性)，与DEM三维离散点数据集合并，在河网层次化选取基础上，利用改进的3D_DP算法对合并数据集进行综合操作。通过试验结果的对比和分析表明，该方法通过弯曲调节指数的调节使河流自身所具有的弯曲形态与地形的主要特征得以同时保留，试验效果良好，实现了三维空间河网要素与DEM数据在同一简化因子作用下的综合，提升了地图综合的质量。

关键词：弯曲调节指数；三维 Douglas-Peucker算法；地图综合

Douglas-Peucker(DP)算法是目前最具代表意义的二维线状要素化简算法[1-2]。目前，部分学者将其从二维推广至三维，提出了三维Douglas-Peucker算法(3D_DP算法)，并应用于DEM的综合[3-5]；文献[6]对算法进行了改进。随后，3D_DP算法在许多领域得到了广泛应用，如黄土高原的地貌综合[7]、等高线间接综合[8-9]、DEM地形特征的提取[10]、规则格网地形的LOD建模[11]及其海底多波束测深数据的抽稀[12]等。这些研究证明该算法能够保持制图区域的主要地貌特征，删除次要地貌，对隐含在DEM中的地貌结构线并没有破坏作用[3]。

河流与地貌在地理成因上存在着天然的耦合关系[13]，以往针对河网与DEM数据的综合研究中，两要素都是分开独立进行的，即河网作为矢量要素是依据其空间几何特征，而DEM则是根据其地形粗糙度，综合标准的不一致可能会在分析操作中出现几何或拓扑矛盾[14]。本文利用3D_DP算法进行河网线要素和DEM的综合方法研究，使两要素在同一简化因子的作用下进行综合操作。在使用3D_DP算法进行两要素综合的过程中，河流在水平方向上自身所具有的弯曲形态将不能同时得以保留，尤其在局部平坦地区表现会更加突出，可能出现在某一阈值下，具有不同大小弯曲的河流要素点全部被综合的情况。

为此，本文引入了“弯曲调节指数”来改进3D_DP算法，提出一种三维空间河网要素和DEM综合的方法。在该方法中，将河网线要素提取成三维离散数据点集(增加高程属性)与DEM三维离散数据点集合并，然后基于改进的3D_DP算法进行综合操作，并利用河北保定及周边地区的河网数据和DEM，对所提算法及应用的正确性和有效性进行了试验验证和分析。

13D_DP算法原理

3D_DP算法实现步骤[3](如图1)为：

(1) 确定原点和首基面：遍历某指定三维离散点集中的所有离散点并两两求矢量积，确定矢量积绝对值最大的一对所确定的平面为首基面，并指定此最大矢量积的3个点分别为原点、初始锚点和初始漂浮点(分别对应图1中的O点、A点和B点)。

(2) 点集有序化：按照空间临近原则对无序的三维离散点进行排序处理。即将初始锚点A作为点列首点，然后依次寻找三维距离最近的下一个新点，最后将初始漂浮点B作为点列的末点，原点O不参与排序。

(3) 特征点的选取：计算排序的每个离散点到首基面的点面距，若最大的点面距小于规定的阈值，则删除所有的点；若最大的点面距大于规定的阈值，则将有序点集从该点分为两段，重复上述过程[3]。

图1　3D_DP算法中的首基面与点面距Fig.1　Initial base plane and point-plane distance of the 3D_DP algorithm

2利用弯曲调节指数对3D_DP算法的改进

本节引入“弯曲调节指数”，使其能够区别反映出河流自身形态中的弯曲的大小，并用它来调节3D_DP算法中的点面距，从而得到伪点面距，然后使用伪点面距与预先设置的阈值进行比较来决定河流要素点的取舍，最终实现河流自身整体形态与地形主要特征的同时保留。

2.1河流弯曲大小的判定和比较

弯曲是线状河流目标形态综合的基本操作单元，一条河流包含有很多大小不一的弯曲。在计算机环境下，需要对弯曲做出数学化的定义，从而能够对弯曲的大小进行合理的划分和识别[15]。

弯曲判定的方法有多种，本文选用了基于拐点的弯曲定义[16]。弯曲由很多线段组成，而每相邻的两线段之间都有一个转折角，或正或负，本文规定逆时针为“+”，顺时针为“-”，当沿着线段前进，转折的方向发生改变时，转角的正负性会发生改变，转角发生改变的这个点称为曲线的拐点。在拐点处，曲线转角发生改变其实就是弯曲发生改变的地方。如图2所示，可以判定P2点、P3点为曲线上的拐点，弯曲在拐点发生了转向，而P1P2段为逆时针弯曲，P2P3段则为顺时针弯曲。基于拐点的弯曲定义具有如下两个特性：①正角弯曲和负角弯曲相间出现；②弯曲是相邻的，涵盖了曲线的所有点。

这里借助弯曲的宽度w、弯曲的长度l、弯曲的面积s、面积系数e和弯曲度f来描述弯曲所具有的特征：①弯曲的宽度w，即弯曲的口径，如图2中的P2P3直线段；②弯曲的长度l，P2P3之间弧段的总长度；③弯曲的面积s，弯曲的长度l与宽度w所围的面积；④面积系数e，e=s/s0，s0为与弯曲周长等长的圆面积，e表示弯曲的凹凸程度；⑤弯曲度f，弯曲的长度l与宽度w的比值称为弯曲度，即f=l/w。弯曲度的最小值是1，值越大，说明弯曲程度越大。

图2　基于拐点的弯曲Fig.2　The bending based on the turning point

2.2弯曲调节指数

为了合理的表示并比较出曲线上每个弯曲的大小，充分体现弯曲长度和弯曲面积的大小对曲线弯曲的影响程度，并让其具有唯一值，本文使用面积系数e、弯曲度f、弯曲长度比及弯曲面积比等几个要素组合构成弯曲调节指数(bending adjustment index)B，即

(i=1,2，…，n,为弯曲的序号)

(1)

假定dk为3D_DP算法中点Pk到基面的点面距，C为弯曲调节常数，则具有弯曲的河流点的伪点面距为

Dk=dk×(C×Bi+1)

(2)

本文在综合时以基本的弯曲作为保留或删除的单元，因此同一弯曲上的所有点使用相同的“弯曲调节指数Bi”，这样可以在综合后从视觉上保持河流弯曲的连续性，并保留弯曲本身的特性不发生变化。

通过式(2)可以看出，若想让弯曲调节指数不起作用，可以令弯曲调节常数C取值为0，这时伪点面距就等于实际的点面距；C的取值也不能过大，如果太大，会使河流点的数量保留过多，影响数据的简化效果。因此，对于C的取值，需要根据具体的地貌形态并通过试验方可确定。

2.3地形地貌的划分

采用弯曲调节指数来调节点面距，是为了避免尤其是平坦地区的河流在与DEM综合时被过度综合。弯曲调节指数调节程度的大小与地形地貌的类别有很大关系，通常来说，地势平坦的地区，调节程度大，而地势陡峭的地区，调节程度小，因此，需要进行地形地貌类型的划分，以区分弯曲调节指数在不同地形类别上对河流段的不同调节作用。

我国地域广阔，各个地区的地形地貌的类别划分有很大不同，本文将试验区选在了河北省保定地区及周边，结合国家习惯上对平原、山地的划分标准[17]，对本文试验区制定了地形类别的划分标准，具体见表1。针对各类地形状况通过试验确定C值的大小。

表1地形地貌类别的划分标准及对应C值的命名

Tab.1StandardsforthedivisionofgeomorphologyandthecorrespondingCvalue

地形类别划分平原丘陵低山区高山区海拔高度/m0～500500～10001000～3000弯曲调整常数命名C1C2C3

3河网要素和DEM数据综合算法

关于河流的综合，一般情况是先执行选取操作，然后再对保留的河流进行化简处理。本文也遵循了地图综合的这一规则，并选择了最具形状代表意义的树状河流进行试验研究。

3.1层次化的河网综合选取

河流的选取是一个复杂的问题，目前也有很多经典的河流选取方法。文献[18]以河流长度为主要标准，辅以河网密度和河流所处层次等标准进行组合，从而进行河流的综合指数的计算。本文引用了这一方法，即

综合指数=长度×等级α×(最大层次-层次+1)β

(3)

式中，河流密度以等级表示；层次值取决于河系树结构，主流所在层次为1，由主流到支流再到次级支流其层次值逐渐增大；α、β为经验参数。综合指数能够保证长度大、所处层次高、支流密度大的河流被优先选取。本文选取了文献[18]中试验确定的数值α=0.3、β=0.7，结果较为满意。按照式(3)计算出每条河流的综合指数，并按综合指数由大到小的顺序对河流进行排序，然后根据需要进行河流的合理选取，河网的层次化分级部分结果如图3所示。

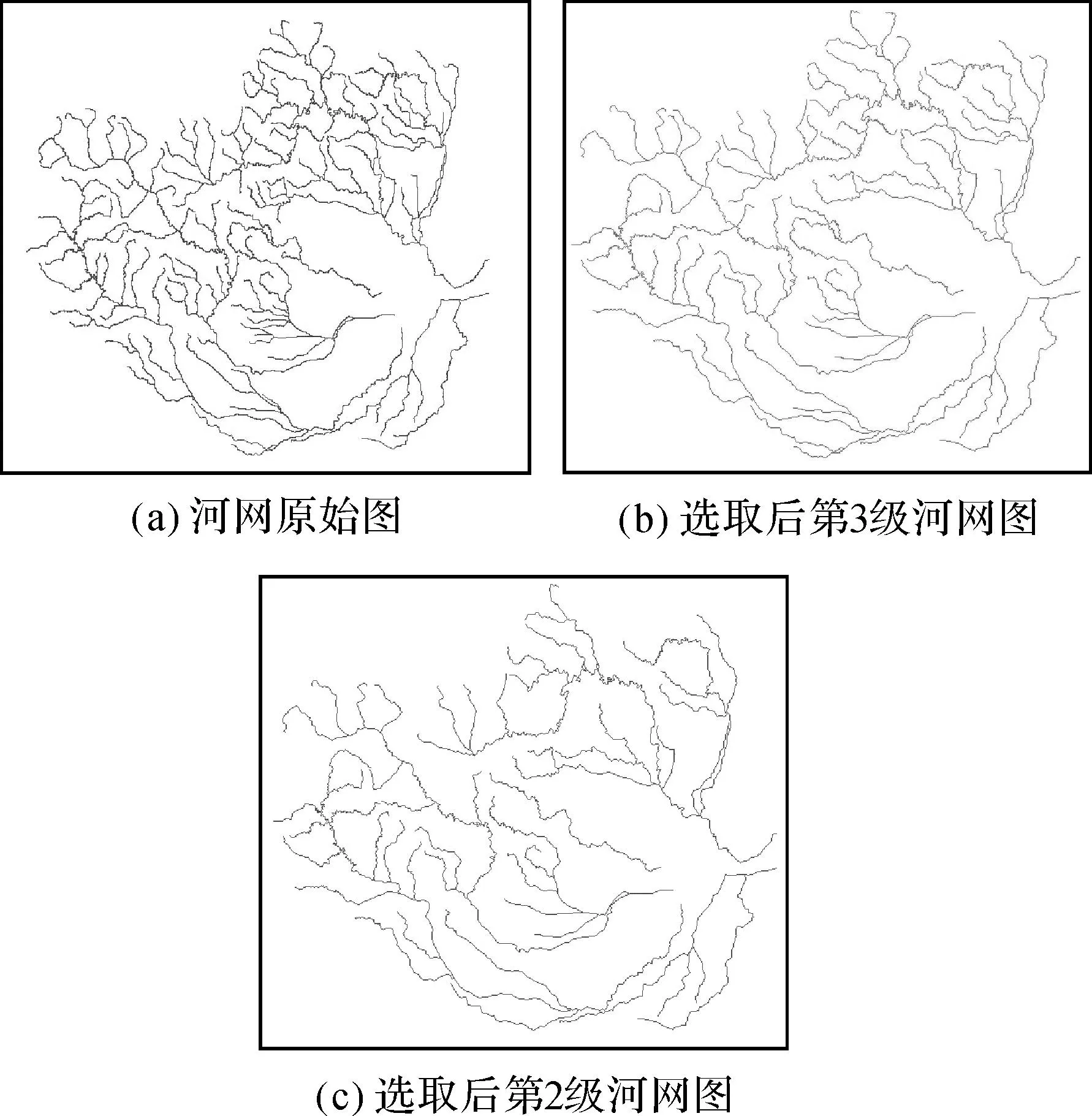
图3　河网层次化选取后各级效果图Fig.3　The effect of levels after river network selection

3.2河网要素和DEM的综合

本文所采用的三维空间河网线要素与DEM综合算法的基本思想是依据河网对地形的高度依附性，将河网数据和DEM数据均提取为三维离散点数据集，合并成同一数据集，然后使用改进后的3D_DP算法进行综合操作。具体综合过程如图4所示。

河网数据通常均为二维矢量数据，首先将河网数据按照3.1节所述方法进行层次化分级后，提取为离散点集，然后与DEM数据叠加增加其高程属性，成为三维离散点集。

使用改进后的3D_DP算法对合并数据集进行综合时，其对DEM点集的综合能够直接根据3D_DP算法的简化阈值的大小自动保留主要地貌特征，删除次要地貌。对河网点集的综合操作，则有如下说明：

(1) 需要加入相应的河流综合规则，即河网完成层次化选取后，已经得以保留的河流不应该在综合时再由于阈值的偏大等原因而被全部简化掉，因此制定以下规则：①在某一层次进行综合操作时，所有河系的主流、支流的起点和终点必须保留；②所有主流和支流的交点也必须保留。

(2) 要获得令人较满意的河网综合结果，需要多次通过试验效果的对比来确定3D_DP算法的简化阈值和弯曲调节常数C的取值。

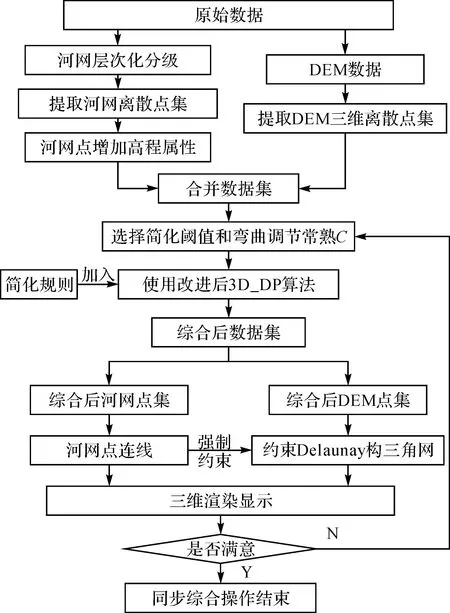
图4　河网要素与DEM综合方法流程图Fig.4　Flowchart of generalization between rivers network and DEM

合并数据集在综合操作完成以后，按照点集的属性重新分离为“综合后河网点集”和“综合后DEM点集”，然后进行河流和DEM的重建。DEM的重建采用Delaunay构三角网的方法进行，实际上重构三角网的过程由于在空间拓扑关系上与河流并没有直接的关系，若重建时不加考虑则不可避免的会出现“河流爬坡”的空间冲突现象，见图5(a)。因为河流一般流经谷底，可以认为是山地隐性的山谷线的一部分，故本文利用综合后的河流线段作为重构三角网的约束边，采用约束Delaunay构三角网的方法[19-20]，使得“河流爬坡”的空间冲突现象得以消除，具体消除情况见图5(b)。

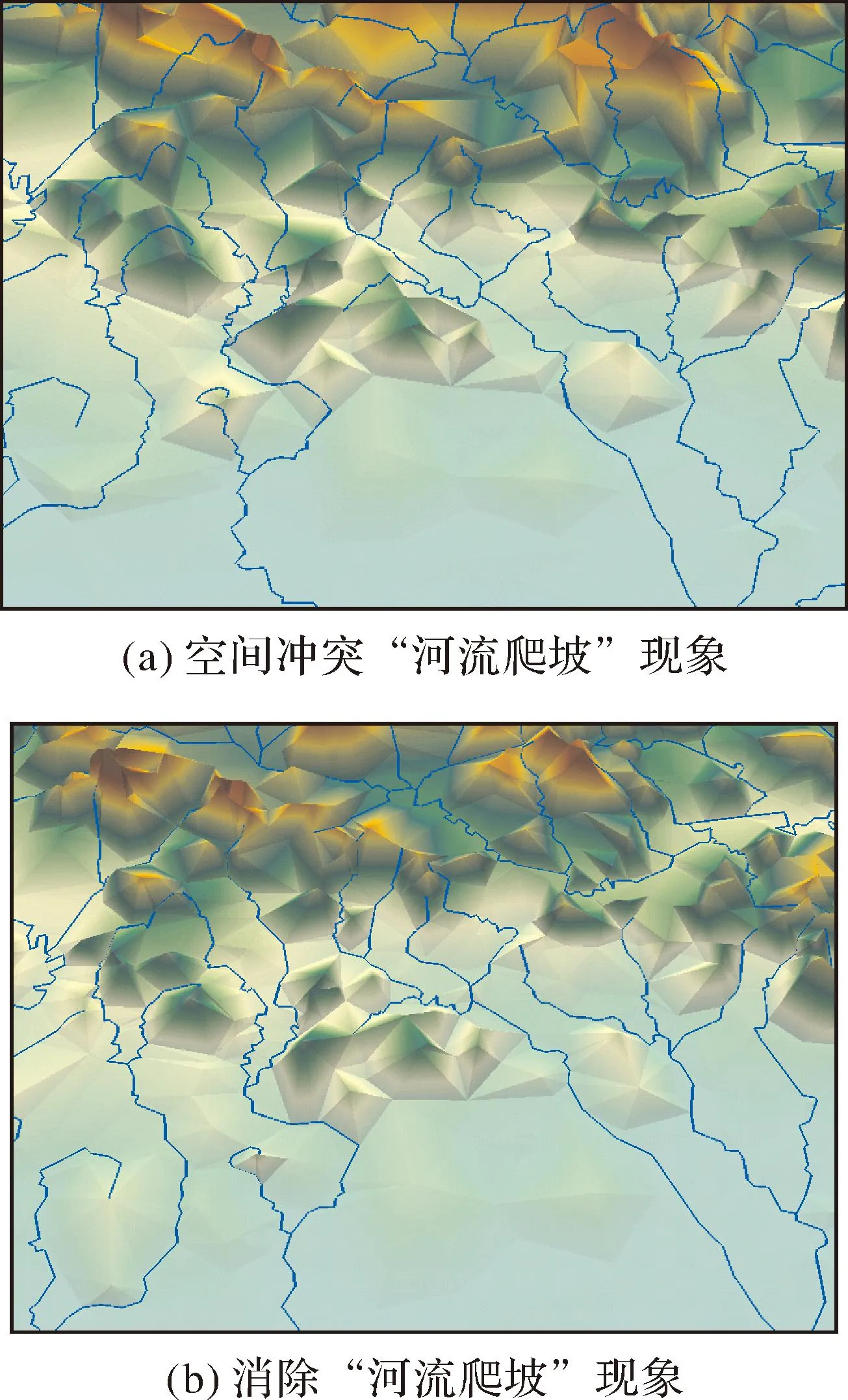
图5　采用约束Delaunay构三角网法消除空间冲突现象Fig.5　The spatial conflict phenomenon is eliminated by constraint Delaunay method

4试验及分析

4.1数据准备与预处理

本研究采用C#编程实现了改进的3D_DP算法、河系树的自动构建、河流综合指数的计算和河网与DEM数据的综合算法等，并使用OpenGL渲染显示综合前后的河网与地形效果图。试验区域和数据选择了河北省保定地区及周边约50 000 km2区域的DEM数据和同一地区的河流矢量数据。该区域地势由西北向东南倾斜。地貌分山区和平原两大类。西北部分以山区为主，东南部分以平原为主，高程分布为8～2893 m；本文对试验区内的微小河流段进行了删除处理，保留了5条完整的树状河系，共有各级河流131条，如图6所示。

按照试验要求对数据进行了预处理，可以通过开方根公式确定综合时某一层次河流被保留的条数。将试验区按照地形地貌分为3类：平原、低山区和高山区，高程划分标准见表1。

4.2试验研究与分析

针对本试验区，根据数据简化百分比和试验预期要求，本文采用3D_DP算法的3个简化阈值200 m、500 m和800 m以及3种地貌分区的弯曲调节常数C1、C2、C3分别对应不同的取值进行了多次试验和结果对比，并选取了弯曲调节指数在综合过程中的调节作用发挥较好的3组进行了统计，具体数据见表2。限于文章篇幅，本节选用阈值为800 m，弯曲调节常数取值C1=2、C2=C3=0.75调节的试验效果图进行展示对比(图7)。图中线型表示试验区部分河流，红色为河流原始形状，蓝色为未使用弯曲指数调节的综合结果，黑色为使用弯曲调节指数后的综合结果。

图6　试验区DEM与河网原图Fig.6　The original image of rivers and DEM in experimental area

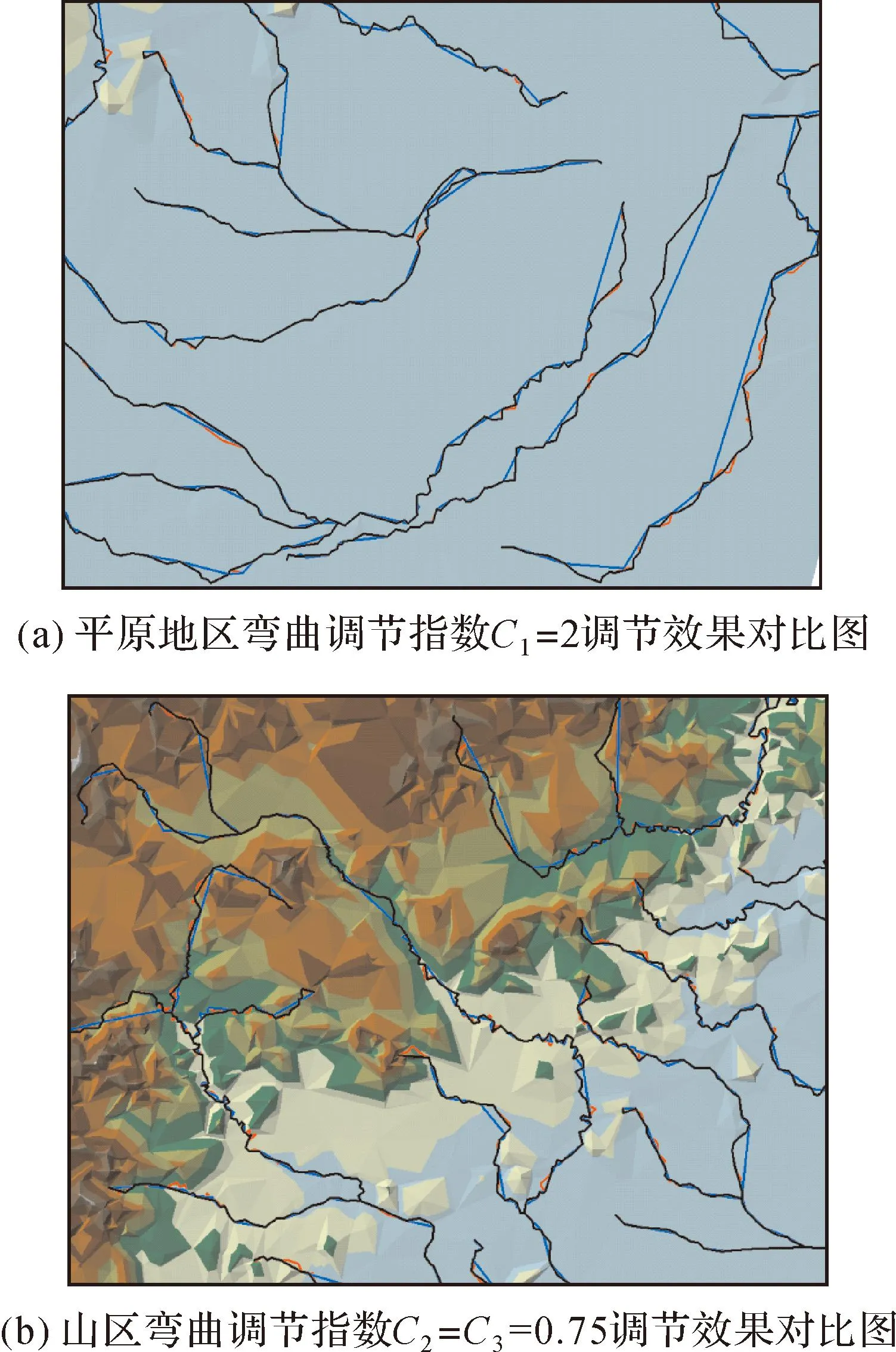
图7　阈值为800 m时河网和DEM综合试验结果对比图Fig.7　Contrast among the simultaneous simplified results of rivers and DEM when the threshold for 800 m

通过以上对试验结果和统计数据的对比，可以得出以下结论:

(1) 本文提出的基于改进的3D_DP算法的河网要素与DEM综合新方法是可行并有效的。该方法中，通过“弯曲调节指数”的调节，河网自身的弯曲形态与DEM的地形特征得以同时保留，实现了三维空间河网要素与DEM在同一简化因子作用下的综合，效果良好。本方法提高了地图综合的质量，拓宽了3D_DP算法应用范围，为进一步扩充矢量数据要素类型与DEM进行综合研究提供了新方法和新思路。

(2) 通过弯曲调节指数的调节，河流数据点的保留点数会增加，通过牺牲一点简化率来提高地图综合整体的质量是可行的。同时由于保留的河流数据点参与3D_DP算法过程中的基面选择，因此DEM数据的保留点数也会有微小的变化，但对整体的综合结果不会造成影响。

(3) 弯曲调节常数C的取值与多方面因素有关，如3D_DP算法所取简化阈值的大小、试验区的地形地貌类别以及地势的相对起伏程度等。因此，对于具体地区应用时，需要通过试验确定其取值。随着3D_DP算法的简化阈值的增大，即数据保留率的降低，弯曲调节指数的调节作用就越趋明显，弯曲调节常数C的取值也趋于增大；通过统计河流点数在调节前后的保留率差值并根据制图综合实际需要，可以适度调整弯曲调节常数C的取值。

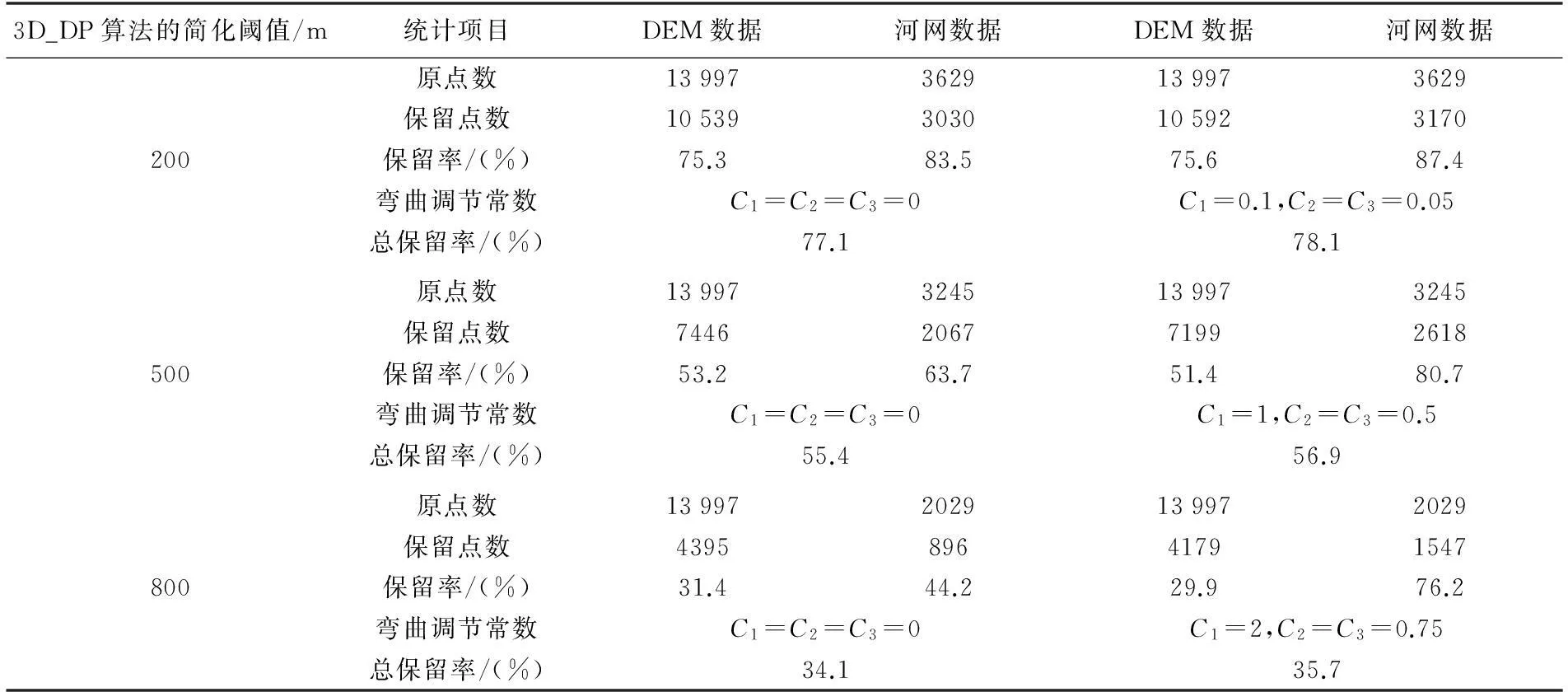
表2　综合算法试验数据统计表

5结论

本文引入“弯曲调节指数”改进了传统3D_DP算法，提出了一种三维空间河网要素和DEM综合的新方法，并通过相关试验分析，得出如下结论：①通过“弯曲调节指数”的调节，使河网自身的弯曲形态与DEM的地形特征得以同时保留，初步实现了两种要素在同一简化因子作用下的同步综合操作，提高了地图综合的质量；②应用弯曲调节指数，使河流和DEM数据点的保留点数会有少许增加，但对整体的综合结果不会造成影响；③河网要素和DEM在同一简化因子下的渐进离散点选取过程，有利于多要素的多层次动态式综合，可为他们建立LOD(细节层次)模型提供不同精度要求的综合数据。

目前在试验结果中，当正角弯曲和负角弯曲连续交替出现形成“复合弯曲”时会出现个别过度综合现象，针对“复合弯曲”的严密数学定义、表达及如何进一步完善弯曲调节指数，将是下一步研究工作中首先要解决的问题。另外，对于综合试验结果好坏的判定只能通过视觉观察确定，存在一定的主观性，需要发展严密的数学方法和模型对其进行定量的描述和评价，且对空间多种地理要素与DEM之间的综合算法的研究还有待于进一步完善与发展，如将更为广泛的其他线状地物如道路、电力线、行政边界线等纳入到综合方法的范畴之中，将有助于此算法的进一步发展和多要素数据综合理论的进步，这些问题将在以后的工作中进行更深入的研究和探讨。

参考文献：

[1]DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973, 10(2): 112-122.

[2]杨得志, 王杰臣, 闾国年. 矢量数据压缩的Douglas-Peucker算法的实现与改进[J]. 测绘通报, 2002(7): 18-22.

YANG Dezhi, WANG Jiechen, LÜ Guonian. Study of Realization Method and Improvement of Douglas-Peucher Algorithm of Vector Data Compressing[J]. Bulletin of Surveying and Mapping, 2002(7): 18-22.

[3]费立凡,何津,马晨燕,等. 3维Douglas-Peucker算法及其在DEM自动综合中的应用研究[J]. 测绘学报, 2006, 35(3): 278-284.

FEI Lifan, HE Jin, MA Chenyan, et al. Three Dimensional Douglas-Peucker Algorithm and the Study of Its Application to Automated Generalization of DEM[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 278-284.

[4]LI Yang, HU Peng, FAN Qingsong, et al. The Generalization Based on 3 Dimensional Douglas-Peucker Algorithm in New DEM Model[C]∥Proceedings of International Workshop on Education Technology and Training and International Workshop on Geoscience and Remote Sensing. Shanghai: IEEE, 2008: 283-286.

[5]FEI Lifan, HE Jin. A Three-dimensional Douglas-Peucker Algorithm and Its Application to Automated Generalization of DEMs[J]. International Journal of Geographical Information Science, 2009, 23(6): 703-718.

[6]何津, 费立凡. 再论三维Douglas-Peucker算法及其在DEM综合中的应用[J]. 武汉大学学报(信息科学版), 2008, 33(2): 160-163.

HE Jin, FEI Lifan. Further Study on Three Dimensional Douglas-Peucker Algorithm and Its Application to Generalization of DEM[J]. Geomatics and Information Science of Wuhan University, 2008, 33(2): 160-163.

[7]刘敏. 基于三维道格拉斯改进算法的地貌自动综合研究——以在黄土高原的实验为例[D]. 西安: 西北大学, 2007.

LIU Min. Relief Automated Generalization Based on the Improved Three Dimensional Douglas-Peucker Algorithm: A Case Study in the Loess Plateau[D]. Xi’an: Northwest University, 2007.

[8]黄丽娜,费立凡. 采用3D D-P算法的等高线三维综合实验研究[J]. 武汉大学学报(信息科学版), 2010, 35(1): 55-58.

HUANG Lina, FEI Lifan. Experimental Investigation on the Three Dimension Generalization of Contour Lines Using 3D D-P Algorithm[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 55-58.

[9]何津,费立凡, 黄丽娜, 等. 三维Douglas-Peucker算法的等高线间接综合方法研究[J]. 测绘学报, 2013, 42(3): 467-473.

HE Jin, FEI Lifan, HUANG Lina, et al. Study on the Method of Indirect Generalization for Contour Lines Based on the 3D Douglas-Peucker Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 467-473.

[10]朱雪坚, 叶远智, 汤国安. 运用三维Douglas-Peucker算法提取DEM地形特征[J]. 测绘通报, 2014(3): 118-121. DOI: 10.13474/j.cnki.11-2246.2014.0105.

ZHU Xuejian, YE Yuanzhi, TANG Guoan. Three Dimensional Douglas-Peucker Algorithm Based Extraction of Topographical Features from DEM[J]. Bulletin of Surveying and Mapping, 2014(3): 118-121. DOI: 10.13474/j.cnki.11-2246.2014.0105.

[11]张俊峰, 费立凡, 黄丽娜, 等. 利用3D_DP和Quad_TIN的地形实时动态显示算法研究[J]. 武汉大学学报(信息科学版), 2011, 36(3): 346-350.

ZHANG Junfeng, FEI Lifan, HUANG Lina, et al. Real-Time Dynamic Rendering Algorithm of Terrain Using 3D_DP Method and Quad_TIN Model[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 346-350.

[12]窦世卿, 刘成军, 林亚文, 等. 基于改进的三维Douglas-Peucker算法的多波束测深数据抽稀方法[J]. 科技导报, 2014, 32(19): 21-25.

DOU Shiqing,LIU Chengjun,LIN Yawen,et al. A Method of Multi-beam Echo Sounding System Data Thinning Based on Improved 3D Douglas-Peucker Algorithm[J]. Science & Technology Review, 2014, 32(19): 21-25.

[13]舒方国. 基于多Agent的等高线与河流协同综合方法研究[D]. 南京: 南京师范大学, 2012.

SHU Fangguo. Collaborative Map Generalization Method of Contours and Rivers Based on Multi-agent[D]. Nanjing: Nanjing Normal University, 2012.

[14]YANG Ling, ZHANG Liqiang, KANG Zhizhong, et al. An Efficient Rendering Method for Large Vector Data on Large Terrain Models[J]. Science in China Information Sciences, 2010, 53(6): 1122-1129.

[15]李雯静, 邱佳, 林志勇, 等. 曲线弯曲识别与等高线簇结构化方法[J]. 测绘学报, 2013, 42(2): 295-303.

LI Wenjing,QIU Jia,LIN Zhiyong,et al. Approach of Curve Bends Recognition and Contour Cluster Structuralization[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 295-303.

[16]沈志峰. 电子海图岛屿多边形简化与合并算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.

SHEN Zhifeng.Research on Simplification and Aggregation Algorithm of Island Polygon in Electronic Chart[D]. Harbin: Harbin Engineering University, 2009.

[17]中国科学院地理研究所. 中国1∶1 000 000地貌图制图规范[S]. 北京: 科学出版社, 1987.

Institute of Geography Research of CAS. 1∶1 000 000 Geomorphologic Map Drawing Specification of China[S]. Beijing: Science Press, 1987.

[18]张青年. 顾及密度差异的河系简化[J]. 测绘学报, 2006, 35(2): 191-196.

ZHANG Qingnian.Generalization of Drainage Network with Density Differences[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 191-196.

[19]杨敏, 艾廷华, 刘鹏程, 等. 等高线与水网数据集成中的匹配及一致性改正[J]. 测绘学报, 2012, 41(1): 152-158.

YANG Min, AI Tinghua, LIU Pengcheng, et al. The Matching and Consistency Correcting in the Integration of Contour and River Network[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 152-158.

[20]龙毅, 曹阳, 沈婕, 等. 基于约束D-TIN的等高线簇与河网协同综合方法[J]. 测绘学报, 2011, 40(3): 379-385.

LONG Yi, CAO Yang, SHEN Jie, et al. Cooperative Generalization Method of Contour Cluster and River Network Based on Constrained D-TIN[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 379-385.

(责任编辑：张艳玲)

修回日期： 2015-12-16

First author： DOU Shiqing(1977—)，female，PhD，associate professor，majors in the generalization and modeling for 3D GIS.

E-mail： 37929972@qq.com

E-mail： zxs@cumtb.edu.cn

The Three Dimensional Douglas-Peucker Algorithm for Generalization between River Network Line Element and DEM

DOU Shiqing1, 2,ZHAO Xuesheng1,LIU Chengjun2,LIN Yawen3,ZHAO Yanqin4

1. College of Geoscience and Surveying Engineering, China University of Mining &Technology (Beijing), Beijing 100083, China； 2. College of Mining Engineering, Heilongjiang University of Science and Technology, Harbin 150022, China； 3. Beijing Forestry Information Technology CO., LTD, Beijing 100036, China； 4. College of Computer and Information Engineering, Heilongjiang University of Science and Technology, Harbin 150022, China

Abstract：At present, the three dimensional Douglas-Peucker (3D_DP) algorithm is mainly used on generalization of a single type of DEM. This paper introduces the “bending adjustment index” to improve the 3D_DP algorithm, and puts forward a new method for generalizing river network and DEM in three-dimensional space. In this method, river network line vector data are extracted into 3D discrete point data sets which are added elevation attributes, and then they are merged with the 3D discrete point data sets of DEM. The generalization operations are made by the improved 3D_DP algorithm after the hierarchical selection of river networks. Through the contrast and analysis of the experimental results, the well experiment results have been achieved. Under the role of bending adjustment index, the overall distribution form of the rivers and the main terrain features can be reserved reasonably on the generalization. The river network and DEM data were generalized under the same simplified factor in this method. It improves the quality of the cartography generalization.

Key words：bending adjustment Index； 3D Douglas-Peucker algorithm； cartography generalization

Corresponding author：ZHAO Xuesheng

通信作者：赵学胜

第一作者简介：窦世卿(1977—)，女，博士，副教授，研究方向为三维GIS综合与建模。

收稿日期：2014-11-18

基金项目：国家自然科学基金(41171306)；黑龙江省自然科学基金(F201436)

中图分类号：P208

文献标识码：A

文章编号：1001-1595(2016)04-0450-08

Foundation support： The National Natural Science Foundation of China (No.41171306 )；Natural Science Foundation of Heilongjiang Province (No.F201436)

引文格式：窦世卿，赵学胜，刘成军,等.河网线要素与DEM综合的三维Douglas-Peucker算法[J].测绘学报，2016,45(4)：450-457. DOI:10.11947/j.AGCS.2016.20140584.

DOU Shiqing,ZHAO Xuesheng,LIU Chengjun,et al.The Three Dimensional Douglas-Peucker Algorithm for Generalization between River Network Line Element and DEM[J]. Acta Geodaetica et Cartographica Sinica,2016,45(4):450-457. DOI:10.11947/j.AGCS.2016.20140584.