Numerical Study on Hydrodynam ics of Ships in Oblique M otion with M ulti-Degree of Freedom

WANG Hua-ming,LÜ Jun,CHEN Lin,WU Bao-shan,ZHAO Chun-hui

(1a.School of Naval Architecture&Ocean Engineering,Key Laboratory of Offshore Engineering Technology of Zhejiang; 1b.Donghai Science and Technology College,Zhejiang Ocean University,Zhoushan 316022,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

Numerical Study on Hydrodynam ics of Ships in Oblique M otion with M ulti-Degree of Freedom

WANG Hua-ming1a,LÜ Jun1a,CHEN Lin1b,WU Bao-shan2,ZHAO Chun-hui1a

(1a.School of Naval Architecture&Ocean Engineering,Key Laboratory of Offshore Engineering Technology of Zhejiang; 1b.Donghai Science and Technology College,Zhejiang Ocean University,Zhoushan 316022,China;2.China Ship Scientific Research Center,Wuxi 214082,China)

It is of significance for the safety of ship to predict the hydrodynamic forces on ship in oblique motion with multi-degree of freedom.In this work,the free-surface viscous flow around ship in oblique motion with multi-degree of freedom is simulated by coupling the equations of ship motion with the Reynolds Averaged Navier-Stokes(RANS)equations.The free surface is modeled by using Volume-of-Fluid(VOF)approach and a high-resolution interface-capturing scheme.The calculated forces and moments are used to determine the dynamic equilibrium position of the ship at the specified speed.Hereby,the running attitudes including the sinkage,trim and heel are obtained. The computations presented here are an effort to numerically simulate the cases as the same as the experiments reported by IWOA(The University of Iowa),and validation of the present method is verified by comparing the present numerical results and measurements.Two sets of simulations are performed,including the model-fixed condition and the model-free condition.Comparisons between the model-fixed condition and model-free condition can enable the identification of the sinkage-,trimand heel-induced effects.The detailed flow field characteristics including the forebody vortex,bilge vortex,pressure distribution on the hull surface are obtained,which are helpful to understand the mechanism causing the change of running attitude in ship’s oblique motion.

numerical simulation;oblique motion;muti-degree of freedom motion; viscous flow;VOF

0 Introduction

Owing to the rudder steering and external forces,such as ocean current or wind etc.,inevitably,the surface vessels always undergo the oblique motion.The viscous hydrodynamic performance of the ship in oblique motion is completely different from that in straight-ahead motion.In the flow field,the flow pattern around a ship is dominated by cross flow,which makesthe flow field around the hull asymmetrical.Meanwhile,the flow separation in the wake flow is more complex.For the running attitude,besides the sinkage and trim undergone in the straight-ahead motion,the considerable heel may occur in the oblique motion.So,focus should be put on the hydrodynamic characteristics of ship in oblique motion with muti-degree of freedom so as to exactly assess the stability and manoeuvring performance of the ship.The studies on oblique motion are traditionally carried out by experimental method,which have a merit of accuracy,but demerit of longer time and higher cost.Typically,Nishio et al(1988)[1]performed the measurements including force and moment,surface pressure and mean velocity for a double-tanker model ship in a wind tunnel.Okuno et al(1989)[2]measured pressure distribution and velocity of the flow around a container model ship in a circulation water channel. Longo et al(2002)[3]conducted the towing tank tests for the Series 60 Cb=0.6 ship model,in which the free-surface elevations and mean velocity at sufficient resolution,resistance,side force,drift moment,sinkage,trim and heel for a range of Fr and drift angle were procured. Kwang et al(2006)[4]studied the viscous effect on the roll motion of a rectangular structure by PIV experiments and observed the generation and dissipation of the bilge vortex.Meanwhile, potential flow theory based methods,such as the lifting surface theory(Inoue et al,1981)[5]and slender-body theory(Yukawa et al,1998)[6],were adopted to simulate the drift motion under small incident angle widely.Nowadays,with the development of computer’s technology,the viscous flow theory based numerical methods by solving the RANS equations is becoming mature.Turbulent flow around a ship model in steady turn and in steady oblique motion was simulated by Cura Hochbaum(1998)[7].Tahara et al(1998)[8]calculated the total resistance, side force and drift moment on a Series 60 model in model-fixed oblique motion by using Baldwin-Lomax turbulence model.And then a lot of efforts on the viscous flow method have been done by Azcueta(2002)[9],Simonsen et al(2006)[10],Wang et al(2009)[11]and Toxopeus et al(2011)[12].Hereby,many features of viscous flow such as the generation and dissipation of bilge vortex etc.in the ship’s oblique motion is now can be numerically simulated.

In the theoretical calculations mentioned above,most calculations have been made on the assumption that the motions of sinkage,trim and heel could be neglected.In fact,the prediction accuracy depends significantly on the ship’s running attitude.Comparisons between the calculated results using the commercial software FLUENT with experimental data obtained by the planar motion mechanism had been performed by Liu et al(2013)[13].It was found that the error of the hydrodynamic forces was on the order of 25%when the running attitude is ignored.So it is necessary to incorporate the effects of the running attitude into the simulation. In the most numerical studies taking the running attitude into consideration,the motions of sinkage,trim and heel are simulated separately,that is,the coupling effects between them is neglected.For example,Inoue et al(1962)[14]and Jinnaka et al(1962)[15]simulated the turning motion using the coupled equations of the horizontal motions,and the motion of heel was treated alone.Hirano(1980)[16]presented a method to simulate turning motion taking the coupling effect due to heel into consideration.Toxopeus(2013)[17]calculated the sinkage and trim of theKVLCC2 with a 4°drift angle by using STAR CCM+.

In this work,by coupling the motion equations of the ship and the governing equations of fluid flow,numerical simulation of the viscous flow field around a ship in oblique motion taking coupling effect among sinkage,trim and heel into consideration are performed.A series 60 ship model is taken as an example and two sets of simulations are performed,including the model-fixed condition(i.e.without sinkage,trim and heel)and the model-free condition(i.e. with sinkage,trim and heel).Differences between the hydrodynamic forces in the model-fixed condition and model-free condition can enable the identification of the salient sinkage-,trimand heel-induced effects.

1 M athematical formulation and numerical method

1.1 Coordinate systems of ship’s oblique motion

The multi-degree of freedom motions of the ship are described by using the dual coordinate systems,that is,the earth-fixed coordinate OXYZ and the ship-fixed coordinate oxyz.The origin of the right-handed ship-fixed coordinate system is located at the center of gravity of the ship and the x-axis directs forward,y to port and z vertically upward respectively,shown in Fig.1.The hybrid basesand the projection of the x-axis on the X′OY′plane serve to define the rotations and Euler angles φ,θ,ψ.The unit vectoris defined as the product ofandfor.Sinkage is positive for the ship moving upward.Heel is positive for the rotation towards to starboard side.Trim is positive for bow up.

Fig.1 Coordinate systems

1.2 Motion equations of the ship

The translational accelerationis solved in the earth-fixed coordinate system,and the angular accelerationin the ship-fixed coordinate system.The subscripts‘E’,‘S’correspond to the variables in the earth-fixed coordinate system and ship-fixed coordinate system,respectively.

where m is the mass of the ship;andare the force and moment acting on the ship;L is the moment of inertia;is the angular velocity.

The ship’s translational and angular velocities are obtained by integrating theandas shown in Eqs.(5)and(6):

1.3 Governing equations of the fluid flow

Since a coordinate system is fixed to the ship,inertia forces caused by the transformation of coordinate are incorporated into the N-S equations as body forces.The governing equations for turbulent flow in the present study are the continuity equations for mass conservation and unsteady Reynolds-averaged Navier-Stokes equations for momentum transport,as follows:

where ui,ujare velocity component;p andare static pressure and Reynolds stress,respectively;fiis the inertia force;is the angular velocity;is the velocity vector in the ship-fixed coordinate system;is the position vector in the ship-fixed coordinate system;is the freestream velocity vector;andare their time derivatives;aqis the q th fluid’s volume fraction in the cell;ρqis the q th fluid’s density;μ is the dynamic viscosity,and it is defined with the method that is the same as ρ.

The free surface is modeled by using Volume-of-Fluid(VOF)approach and a high-resolution interface-capturing scheme,as follows in Eq.(12):

Closure of the Reynolds stress problem is achieved by using the turbulence model,and two turbulence models(i.e.RNG k-ε and SST k-ω)are investigated and their influences on the numerical results are evaluated.The conservation equations of momentum,mass and turbulence parameters are discretized with the Finite Volume Method(FVM);convective terms are approximated with the second order upwind scheme and diffusive terms with the central differencing scheme;the transport equations for the turbulent kinetic energy and its dissipation rate are discretized with the second order upwind differences;pressure and velocity are coupled by the PISO algorithm.All equations are under-relaxed using a relaxation factor of 0.3.

1.4 Models’principal dimension and computational domain

To facilitate the comparison,two Series 60 models with different dimensions are taken as examples,as shown in Tab.1.The computation domain and its boundary conditions are shown in Fig.2.The inlet boundary is located a length of the ship(L)in front of the ship,while the outlet boundary is located 2L downstream of the ship.The bottom of the domain is located L beneath the ship.Transversely,they reach to 1.5L from the center line of the ship.For the model-fixed condition,the top boundary is located above the deck at a distance equal to the draft.While for the model-free condition,the top boundary is located a half length of the ship above the deck.The prescribed velocities(u=-U cos β,v=-U sin β,w=0)and volume fraction are set on the flow inlet,top,bottom and the far field side at the port side,while the outlet boundary is modeled with a pressure-outlet condition(p=0).During the simulation,it is found that the convergence time could be reduced greatly by using the pressure-outlet condition instead of the velocity-inlet condition for the far field side boundary at the starboard side.The no-slip and impermeability boundary conditions are applied for the hull surface.

Tab.1 Principal dimensions of Series 60(Cb=0.6)

Continue Tab.1

Fig.2 Computational domain and boundary conditions

1.5 Grid generation

The computational grids are shown in Figs.3 and 4.For the model-fixed condition,the grids consist of a single structured block,as shown in Fig.3.The axial resolution of both the hull grids and near-freesurface grids is tightened to capture the detailed flow features,especially for the short waves generated by the ship at low Froude number.For the model-free condition,the hybrid grid technique that combines the structure grids with unstructured grids is adopted,as shown in Fig.4.Similarly,the grids are refined around the hull surface and the expected free surface.The whole domain is comprised of three types of grids,as shown in Fig. 4(b).The first type is the prism grids,which move with the ship as a rigid body.The second one consists of tetrahedral grids in a small rectangular region around the hull,which can be regenerated to capture the running attitude.The updating approaches of the meshes in this region are‘Smoothing’and‘Local Remeshing’.And the third one consists of the stationary hexahedral cells and prism cells far away from the hull.

Fig.3 Computational grids for the model-fixed condition

2 Numerical results and discussion

In order to evaluate the influence of the turbulence model on the numerical results,two turbulence models are chosen respectively to close the RANS equations in the model-fixed condition.The total resistance,side force,drift moment,sinkage,trim and heel of the ship at low Froude number(Fr=0.16)and high Froude number(Fr=0.316)are calculated respectively in the model-free condition.To facilitate a direct comparison,the integral variables are nondimensionalized with Eqs.(13)-(15).

2.1 Cases in model-fixed condition

The selections of congruent turbulence model and study on grid independency are performed.Firstly,Model-1 is taken as the example to investigate the hydrodynamic forces,for its principle dimensions are the same as those used by Tahara(1998)[8].The numerical results of hydrodynamic forces and moment on this model are compared with Tahara’s,and the relative error between them is defined as E%D=(S-D)/D*100,where S is the present result and D is Tahara’s.Three sets of computational grids with different density grids are chosen,which are noted by‘Coarse’,‘Medium’and‘Fine’in Tabs.2-4.There are the same number of prism layers of the grids attached to the hull surface for all the three sets of grids.The cell size increases in all directions outside the prism layer by a factor of 1.2.When the same grid is used,it is found that the calculation by SST k-ω better predicts the hydrodynamic forces.The hydrodynamic force coefficients at the medium and fine grids are very close,and a fairly good agreement is obtained.It can be found that,the numerical results converge at 2.6 million grids number.

Tab.2 Comparisons of the total resistance coefficients(Fr=0.316,β=10°)

Tab.3 Com parisons of the side force coefficients(Fr=0.316,β=10°)

Tab.4 Com parisons of the drift m oment coefficients(Fr=0.316,β=10°)

Then,Model-2 is taken as the example to investigate the wave profiles calculated by different turbulence models,for its principle dimensions are the same as those employed in the experiment by Longo(2002).The present wave profiles on the hull surface of Model-2 are compared with those by Longo,as shown in Fig.5.Obviously,the results by SST k-ω model corresponds better with the experiment than those by RNG k-ε model,and this holds particularly for the wave profiles at port side.While,the trough near the stern cannot be predicted very well by this model on the starboard side.The values of wave elevation calculated by the RNGk-ε model are much larger than those by SST k-ω model and experiments on both port side and starboard side.It can be drawn that the SST k-ω model is more conformable to simulate the flow fields involving asymmetry and separation,and it is adopted in the following calculations of model-free condition.

Fig.5 Comparison of wave profiles by different turbulence models at Fr=0.316 and β=10°

Fig.6 shows the comparison between the calculated wave elevations and those measured in experiment for the case of Fr=0.316,β=10°.It can be found agreement is satisfactory.The results have good predictions of the amplitude and wave pattern.However,the wave damping is serious especially for the port side,which may be contributed to the decrease of grid resolution on the port side.It can be found that the wave contours are asymmetric,and the wake region is also asymmetric with a wedge angle on the starboard side.The highest wave elevation is at the bow with Z/L=0.03 and the minimum wave level is near hull shoulder with Z/L=-0. 015.The predicted maximum wave elevation is the same with the experiment,while the minimum wave elevation under-predicts the measurement by 2.5%.

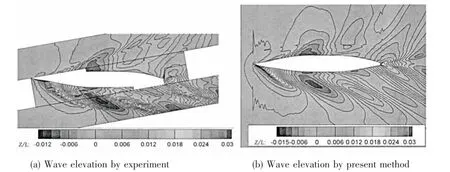
Fig.6 Comparison of wave elevations at Fr=0.316,β=10°

2.2 Cases in model-free condition

Fig.7 shows the convergence histories for integral variables at Fr=0.316,β=10°.It is noted that the simulation shows the strong oscillations in the first few seconds.Convergence to the steady state could be obtained in short time except for heel.Tab.5 shows the results of sinkage,trim,heel and the integral variables together with percent error based on measurements by Longo(2002)[3].The comparison error is defined as E%D=(S-D)/D*100,where D is the EFD value by Longo(2002)and S is the present result.The negative sinkage,trim and heel correspond to the motions of moving downward,bow down and stern up and heeling towards the direction of the windward side respectively.In general,the results of sinkage,trim and heel satisfactorily predict the measured ones,and these hold particularly for the higher speed condition(Fr=0.316)with the errors under the order 10%.While,the errors of sinkage,trim, heel for the lower speed condition(Fr=0.16)are large,typically on the order of 10%or more. The larger errors in the lower speed condition may be attributed to the following reason,that is,the running attitudes of the ship are sensitive to small disturbances.The side force coefficient Csby Cura Hochbaum(1998)[7]under-predicted with the order 11%at Fr=0.16,and he attributed this under-prediction to the lack of the free surface and the dynamic squat and heel.While,in the present study,because effects of trim,sinkage,heel and free surface have all been taken into account,errors of the hydrodynamic forces are smaller than 7%at Fr=0.16 and 5%at Fr=0.316.

Tab.5 Com parisons between computational results and measurements

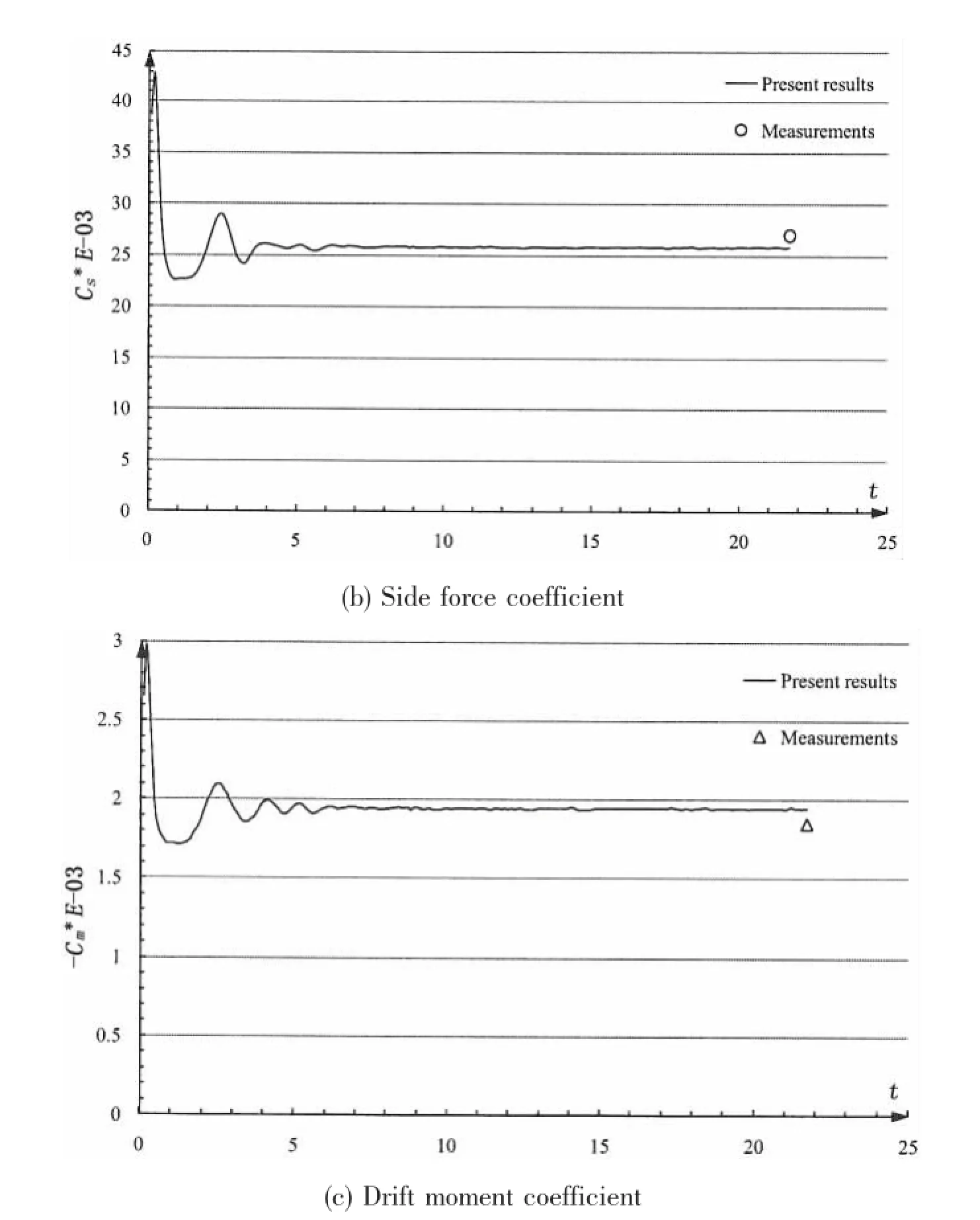
Fig.7 The converge histories for integral variables(Fr=0.316,β=10°)

The velocity distributions of Z direction on the longitudinal and cross sections are shown in Fig.8.Due to the motion of bow-down and stern-up,an obvious fore-body vortex is generated,as shown in Fig.8(a).The Z-velocity at fore-body is negative,which means the bow is moving down.Similarly,the generation of the bilge vortex can be observed obviously,as shown in Fig.8(b),and the Z-velocity on the leeward side is positive and negative on the windward side,which means that the ship is heeling towards the direction of the windward side.The similar generation of the bilge vortex was observed in the work of Kwang et al(2006)[4],in which, the viscous effect on the roll motion of a rectangular structure was investigated through the PIV experiments.

Fig.9 shows the pressure distribution on the hull surface.From Fig.9(a)-(b),it can be seen that the overall pressure on the windward side is larger than that on the leeward side,this is the reason of the side force being generated.Meanwhile,the pressure on the windward side near bow is much larger than that on the leeward side near bow,and this will cause the drift moment.What’s more,it can be found that distributions of pressure on different parts of the hull are asymmetrical,and ship’s heel,trim and sinkage are induced.

Fig.8 The velocity contour(Fr=0.316,β=10°)

Fig.9 Pressure distribution on the hull at t=5 s(Fr=0.316,β=10°)

Fig.10 shows the the wave pattern around the ship in the model-fixed condition at Fr=0. 316 and β=10°,which is measured by Longo et al(2002)[3].While,Fig.11 shows the present numerical results in model-free condition.From these two figures,it can be seen that the characteristics of the wave patterns are very sim ilar including the half-wave envelope angle,diverging wave angle and the wedge-liked angle on the wake region,except that the value of the wave crest near the bow in model-free condition is a little larger than that in model-fixed condition,while the value of the wave trough near the shoulder is a little smaller than that in model-free condition.Wave profiles on the hull are calculated in model-fixed and model-free conditions at Fr=0.316 and β=10°,and they are compared in Fig.12.It can be found that the profiles in these two different conditions are very similar.While,the profile in model-free condition is always above that in model-fixed condition on both port side and starboard side,and this is consistent with the sinkage in model-free condition.

Fig.10 Wave pattern in model-fixed condition

Fig.11 Wave pattern in model-free condition

Fig.12 Comparisons of the wave profiles in model-fixed and model-free conditions(Fr=0.316,β=10°)

3 Conclusions

In the present study,numerical simulations of the drift motion of Series 60 Cb=0.6 ship model in both model-fixed and model-free conditions are carried out.The viscous flow around ship in oblique motion with multi-degree of freedom is simulated by coupling the equations of ship motion with the unsteady Reynolds Averaged Navier-Stokes(RANS)equations,and freesurface is captured by using Volume-of-Fluid(VOF)approach and a high-resolution interface-capturing scheme.The effect of turbulence model on the accurate prediction of the numerical results is investigated in the model-fixed condition.With respected to the comparisons of the results calculated by RNG k-ε turbulence model and SST k-ω model,it is found that both hydrodynamic forces and wave profiles obtained by SST k-ω model agree better with the measurements than those by RNG k-ε model.

In the model-free condition,numerical simulations are carried out at two speeds(Fr=0.16,0.316),respectively.From the comparisons of the present hydrodynamic coefficients with measurements,it is found that the errors of the present results calculated by taking trim,sinkage and heel into account are smaller than 7%at Fr=0.16 and 5%at Fr=0.316,which is an improvement on the previous work.By analyzing the characteristics of flow field obtained in the present work,such as fore-body vortex,bilge vortex and wave elevation,we can clearly see that the effects of fluid’s viscosity and free surface are significant,so it is necessary to consider them in predicting hydrodynamic forces on ships in oblique motion.

Acknow ledgements

This work is supported by the National Natural Science Foundations of China(Grant No. 51109186),Zhejiang Provincial Natural Science Foundations of China(Grant No.LY16E090-004,LY14E090003)and the Open Foundation from Key Laboratory of Marine Fishery Equipment and Technology of Zhejiang(MFET201401).

[1]Nishio S,Tanaka I,Ueda H.Study on separated flow around ships at incidence[J].J Kansai Soc Naval Arch,1988,210: 9-17.

[2]Okuno T,Tanaka N,Hasegawa Y.Flow field measurements around ship hull at incidence[J].J Kansai Soc Naval Arch, 1989,212:67-74.

[3]Longo J,Stern F.Effects of drift angle on model ship flow[J].Experiments in Fluids,2002,32(2002):558-569.

[4]Kwang H J,Kuang A C,Hyo J J.Viscous effect on the roll motion of a rectangular structure[J].Journal of Engineering Mechanics,2006,132:190-200.

[5]Inoue S,Hirano M,Kijima K.Hydrodynamic derivatives on ship manoeuvring[J].International Shipbuilding Progress, 1981,28(321):112-125.

[6]Yukawa K,Kijima K.An estimation of hydrodynam ic forces acting on a ship hull in manoeuvring motion[J].Trans.West-Japan Soc.Nav.Arch.,1998,95:67-79.

[7]Cura Hochbaum A.Computation of the turbulent flow around a ship model in steady turn and in steady oblique motion[C] //Proc.22nd Symp on Naval Hydro.Washington,D.C.,USA,1998:198-213.

[8]Tahara Y,Longo J,Stern F,Himenno Y.Comparison of CFD and EFD for the Series 60 CB=0.6 in steady yaw motion[C]// Twenty-Second Symposium on Naval Hydrodynamics.Washington,D.C.,USA,1998:981-999.

[9]Azcueta R.Computation of turbulent free-surface flows around ships and floating bodies[J].Ship Technology Research, 2002,49(2):46-69.

[10]Simonsen C D,Stern F,Agdrup K.CFD with PMM test validation for manoeuvring VLCC2 tanker in deep and shallow water[C]//In International Conference on Marine Simulation and Ship Manoeuvring(MARSIM).Terschelling,The Netherlands,2006.

[11]Wang H M,Zou Z J,Tian X M.Computation of the viscous hydrodynamic forces on a KVLCC2 model moving obliquely in shallow water[J].Journal of Shanghai Jiaotong University,2009,14(2):241-244.

[12]Toxopeus S,Simonsen C D,Guilmineau E,Visonneau M,Stern F.Viscous-flow calculations for KVLCC2 in manoeuvring motion in deep and shallow water[C]//NATO AVT-189 Specialists Meeting on Assessment of Stability and Control Prediction Methods for NATO Air and Sea Vehicles.Portsdown West,UK,2011:151-169.

[13]Liu H,Ma N,Deng D H,Gu X,Gu X C.Application of circulating water channel in plannar motion mechanism tests and its numerical verification[C]//Proceedings of the 2013 Conference on Ship Hydrodynamics.Xi’an,China,2013:440-448.(in Chinese)

[14]Inoue S,Fukuda J.Maximum heel when the rudder is put over[J].Transactions of the West-Japan Society of Naval Architects,1962,23.(in Japanese)

[15]Jinnaka T,Fukase T,Yumuro A,Yamazaki T.Some treatments on the calculation of turning of ships[J].Journal of the Society of Naval Architects of Japan,1962,111.(in Japanese)

[16]Hirano M,Takashina J.A calculation of ship turning motion taking coupling effect due to heel into consideration[J].Transactions of the West-Japan Society of Naval Architects,1980(59):71-81.

[17]Toxopeus S L,Simonsen C D,Guilmineau E,Visonneau M,Xing T,Stern F.Investigation of water depth and basin wall effects on KVLCC2 in manoeuvring motion using viscous-flow calculations[J].Journal of Marine Science and Technology, 2013,18(4):471-496.

船舶多自由度斜航运动水动力数值研究

王化明1a，吕俊1a，陈林1b，吴宝山2，赵春慧1a

（1.浙江海洋大学a.船舶与海洋工程学院，浙江省近海海洋工程技术重点实验室；b.东海科学技术学院，浙江舟山316022；2.中国船舶科学研究中心，江苏无锡214082）

计及多自由度运动的船舶斜航水动力预报对船舶航行安全具有重要意义。文章通过耦合求解船舶运动方程和雷诺平均N-S方程，并采用VOF方法和高精度自由面捕捉技术对作多自由度斜航运动船舶的粘性绕流场进行数值模拟。船舶动态平衡位置根据计算出的力和力矩来决定，得到包括升沉、纵倾和横倾在内的船舶浮态。文中采用的算例与爱荷华大学进行的模型试验相同，通过比较数值计算结果和试验值验证了该方法的有效性。对船模在受约束和自由运动两种状态下的船舶运动和流场进行模拟，通过比较分析船舶升沉、纵倾和横倾的影响。文中计算获得的详细流场细节特征，包括前体和舭部的涡以及船体表面上的压力，有助于理解船舶斜航运动浮态变化的机理。

数值模拟；斜航运动；多自由度运动；粘性流；VOF

O352

A

王化明（1979-），男，博士，浙江海洋大学船舶与海洋工程学院副教授，硕士生导师；吕俊（1994-），男，浙江海洋大学船舶与海洋工程学院硕士研究生；陈林（1981-），女，硕士，浙江海洋大学东海科学技术学院讲师；吴宝山（1968-），男，中国船舶科学研究中心研究员，博士生导师；赵春慧（1986-），女，硕士，浙江海洋大学船舶与海洋工程学院实验师。

O352

A

10.3969/j.issn.1007-7294.2016.09.002

1007-7294（2016）09-1083-15

Received date：2016-04-26

Foundation item:Supported by National Natural Science Foundations of China(Grant No.51109186),Zhejiang Provincial Natural Science Foundations of China(Grant No.LY16E090004,LY14E090003)and the Open Foundation from Key Laboratory of Marine Fishery Equipment and Technology of Zhejiang(MFET201401)

Biography：WANG Hua-ming(1979-),male,doctor of Zhejiang Ocean University,E-mail:hmwang@zjou.edu.cn.com; WU Bao-shan(1968-),male,researcher/tutor.