模板匹配法与八邻域分析法在数字识别细化预处理中的应用及比较

张盼盼 张颖颖

摘要：讨论了模式识别的基本问题之一——图像的细化处理，将模板匹配法和八邻域分析法应用于数字识别的细化预处理中。着重比较了两种算法在数字识别中的细化结果，指出两种算法在数字识别细化预处理中存在的缺点，认为八邻域分析法适用于数字识别的预处理。对八邻域分析法作进一步改进，消除细化后冗余的像素点，保证了细化结果为单像素连接，确保数字识别的骨架提取预处理，从而提高数字识别速度及准确率。

关键词：数字识别；细化算法；模板匹配法；八邻域分析法

DOIDOI：10.11907/rjdk.161008

中图分类号：TP317.4

文献标识码：A 文章编号：1672-7800（2016）005-0210-02

0 引言

数字识别在车牌号识别、电表读数识别、票据识别等应用中运用广泛，随着计算机技术的高速发展，已有众多学者投入到数字识别的研究中。细化算法是数字识别预处理中的重要环节之一。在进行数字识别之前，为了提取和描述数字特征，往往要先对字符作细化处理，得到数字的细化结构。提取出的“骨架”能很好地突出字符形状的特点，减少冗余信息量，从而减小识别的运算量，提高数字识别的准确率。一个好的细化算法是以细化的质量和速度进行评价的，细化后的骨架应满足以下条件：①骨架的连通性必须与原图像保持一致；②骨架要保持原图像的拓扑结构；③骨架的线条宽度应尽量为单像素；④骨架在原图像几何上处于合适位置，如在中间。

细化算法无论是在图像分析还是图像识别方面都可起到重要作用，近年来许多学者相继提出了各种细化算法，如距离变换法[1，2]和边缘剥离法[3]。距离变换算法可以一次性产生骨架，但是很难保证得到骨架的连通性。因此，现实应用中大多采用边缘剥离法。边缘剥离法是重复地删除边缘上的点，直到得到由单层点构成的图像。边缘剥离算法又可以分为并行和串行两种。在串行算法中，是否删除像素在每次迭代的执行中是顺序固定的，它不仅取决于前次迭代的结果，也取决于本次迭代中已处理像素的分布情况，而在并行算法中，像素的删除与否与像素在图像的横纵顺序无关，仅取决于前次迭代的结果。

本文比较了并行边缘剥离法中经典的模板匹配法[4]和八邻域分析法[5]，将两种算法应用于数字识别的细化处理中。通过对实验结果的分析，指出两种算法在数字识别细化处理中存在的缺点，并对八邻域分析法作进一步改进，以用于数字识别的细化。

1 模板匹配法在细化预处理中的应用

将模板匹配法应用于数字识别的细化预处理中，对包含数字的图片进行一系列预处理操作：分割—去噪—二值化。经过预处理，待细化的图像是0，1二值图像。像素值为1的是需要细化的部分，像素值为0的是背景区域。模板匹配法给出删除条件对应的模板，只要检测的像素点满足被删除的条件，则被删除，删除的条件在模板中给出[6]。

现有一幅要处理的数字字符0的二值图像，按照以上算法对该二值图像进行一次循环，得到的图像如图1（a）所示。由图可知，该细化出现了断裂现象，原因在于原二值图像中存在双边缘目标像素，对于双边缘中每一列目标像素，其U=5，按照该算法，双边缘的每一列都可以被删除，最终导致细化后的图像出现断裂现象。而对于没有双边缘的二值化图像，采用该算法后细化结果良好，未出现断裂现象，如图1（b）所示。

2 八邻域分析法在细化预处理中的应用

将八邻域分析法应用于数字识别的细化预处理中，如图3（a）所示是一幅要处理的数字字符0的二值图像，按照以上算法对其进行细化处理，得到图3（b）所示的细化结果。

3 模板匹配法和八邻域分析法在细化预处理中的比较

由图1的细化结果可以看出，将模板匹配法应用于存在双边缘像素二值图像的细化算法时，细化结果存在断裂现象，且细化结果不是单像素连通，这对于要求得到单边缘像素细化结果的数字识别，模板匹配法的细化预处理不符合条件。因此，很多学者对模板匹配法进行了改进，以消除双边缘造成的影响，但是改进后的算法使得整体复杂度增加，且效果不是很理想。

与模板匹配法相比，八邻域分析法得到的细化结果良好，对于存在双边缘像素的原二值图像，细化结果不存在断裂现象，如图3所示，且细化后的骨架连通性与原图像保持一致，同时骨架在原图像集合位置中间。

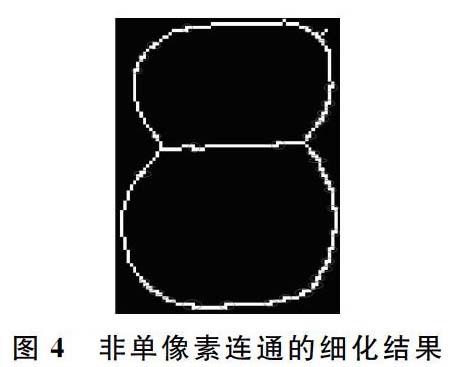
然而，八邻域分析法在数字识别细化预处理中也存在一定缺点。将八邻域分析法应用于复杂图像的细化时，存在无法达到单像素连通细化结果的问题，这将降低后续数字识别的速度和效率。非单像素连通的细化结果如图4所示。

4 改进的八邻域分析法在细化预处理中的应用

采用八邻域分析法对于复杂图像无法达到单像素连通的细化结果，而对于数字识别，单像素的细化骨架能够提高数字识别的速度和准确率，因此本文提出改进的八邻域分析法来消除细化后多余的像素点。

4.1 直角连通情况

经分析可知，由以上算法细化后多余的像素点都是属于直角连通的情况。直角连通情况可归纳为以下两个条件：①当前像素点符合4种直角连通情况之一；②V（i，j）=2。符合以上两个条件则说明当前像素点是直角连通的情况，可将当前点删除。

4.2 直线相交情况

经分析可知，直线相交也是造成细化后图像冗余的另一个原因，直线相交情况则可将当前像素点删除。

将改进的八邻域分析法应用于数字识别细化预处理中，得到的图像骨架连通性与原图像保持一致，且为单像素连通，同时骨架在原图像集合位置中间，这为后续的数字识别提供了最为理想的细化预处理结果。

5 结语

将模板匹配法与八邻域分析法应用于数字识别的细化预处理中，可以看出，模板匹配法对于数字的细化，当出现双边缘像素时则必须结束算法，否则会出现连通区域的断裂现象，将算法改进会消耗更多时间且增加复杂度。而八邻域分析法可以直接获得良好的符合条件的细化结果，有利于后面的数字识别部分，但采用八邻域分析法对复杂图像进行细化时，得到的细化结果并非单像素连通。因此，对八邻域分析法作出改进，将直角连通和直线相交情况造成的冗余点删除，改进的八邻域分析法可以得到数字字符的单像素连通细化骨架，从而提高后续数字识别的速度及准确率。

参考文献：

[1]陈军，杨存建.一种基于分区标记的快速细化方法[J].计算机应用与软件，2008，25（3）：12-14.

[2]任金昌，赵容椿.一种基于标记的并行细化算法[J].电子学报，2009，28（11）：9-12.

[3]野媛.普通Sobel边缘细化算法的改进[J].科技信息，2009（29）：312-313.

[4]毕厚杰，于锡建.一种基于边缘点特征的细化算法[J].数据采集与处理，1990，5（1）：7-11.

[5]吴丹.一种快速准确的细化算法[J].计算机与现代化，2003，1（1）：6-10.

[6]杨兴炜，刘文予，白翔.一种有效的快速细化算法[J].小型微型计算机系统，2006， 27（7）：1343-1346.

[7]喻擎苍，苏斌.改进的符号图像并行细化算法[J].计算机工程与设计，2009，30（3）：723-725.

（责任编辑：黄 健）