控制系统蒙特卡洛方法应用分析

陈磊

摘要：鉴于蒙特卡洛方法在控制系统设计及分析中的广泛应用，对蒙特卡洛仿真的工作流程及关键技术问题进行分析，并给出一种基于MTTLAB分布式计算引擎的控制系统蒙特卡洛仿真方案。

关键词：控制系统；蒙特卡洛；分布式计算；项目管理器

DOIDOI：10.11907/rjdk.161500

中图分类号：TP302

文献标识码：A 文章编号：1672-7800（2016）005-0010-03

0 引言

蒙特卡洛方法是利用随机数进行统计试验，求得统计特征值（如均值、概率等）作为待解问题的数值解，所作的统计试验称为蒙特卡洛仿真或者蒙特卡洛模拟。该方法是众多研究不确定性传递的方法之一，目的是要确定不确定性（包括系统参数变化、建模误差、外界扰动等）如何影响系统性能，其常用于复杂的非线性模型以及具有不确定参数的模型。

蒙特卡洛方法可以解决各种类型的问题，一般来说，该方法处理的问题可以分为两类：第一类是确定性的数学问题。包括计算多重积分、求解逆矩阵、线性代数方程组、积分方程和微分算子的特征值等；第二类是随机性问题，对于这类问题，有时可表示为多重积分或某些函数方程，并进而考虑用随机抽样方法求解。然而，一般情况下都不采用这种间接模拟方法，而是采用直接模拟方法，即根据实际物理情况的概率法则，首先建立一个与求所解有关的概率模型，使所求的解为所建立模型的概率分布或数学期望，然后对该模型进行随机抽样观察，即产生随机变量，最后用其算术平均值作为所求解的近似估计值。

当前，蒙特卡洛仿真及分析方法广泛应用于控制系统设计及分析中，包括制导与控制系统设计缺陷的分析、轨道及特定飞行器参数的识别[1]；飞机鲁棒性分析中实时稳定裕度的测量[2]；鲁棒自动着陆控制律的优化设计[3][4]；电传飞控系统的飞行品质研究[5]等方面。本文对控制系统蒙特卡洛仿真的工作流程及关键问题进行分析，并给出一种控制系统的蒙特卡洛仿真方案。

1 蒙特卡洛仿真工作流程

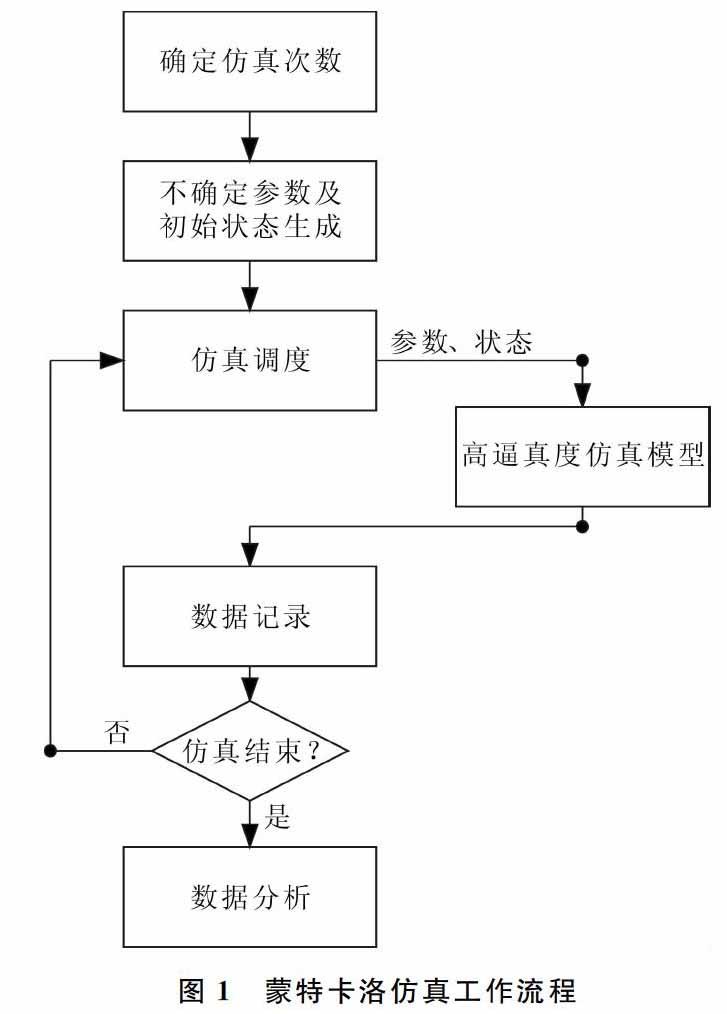
Matlab环境下的蒙特卡洛仿真工作流程如图1所示。

蒙特卡洛工作流程为：①首先确定系统仿真参数，仿真次数可以通过理论分析方法或试验方法确定；②根据不确定性模型生成全部仿真所需的随机偏差和初始状态；③以预设的不确定偏差及初始状态进行仿真调用，并记录所需的结果及状态数据；④仿真全部结束后，对记录的数据进行分析，根据分析结果对仿真模型、控制系统设计进行相应的改进。在蒙特卡洛仿真过程中，需要重点考虑以下问题。

1.1 不确定性建模

大部分实际系统中总是包含有不确定性，蒙特卡洛仿真中需要采用随机数进行统计试验，所以需要建立系统不确定输入的概率模型，即确定不确定输入的分布类型。对于部分不确定性，根据经验或理论分析，可以知道其概率分布形式，但大部分情况概率分布是未知的。对于这类不确定性，较为普遍的方法是采用不确定性参数的标称值均值的正态分布作为不确定性的概率模型。但有些情况下，不确定性明显不服从正态分布，这就需要根据观测样本进行不确定性建模。

假定实际系统不确定性的观测数据为互相独立的随机变量，不确定性建模步骤为：

（1）选择概率分布类型。选择概率分布的依据是随机变量的知识以及占有的数据。很多情况下，可以根据先验知识以及对产生该随机变量过程的认识决定或者拒绝哪种分布。另外，数据对概率选择具有决定性作用。一般有了足够的数据就可以选择出较好的概率分布，至少可以作出经验分布或者半经验分布，而且可以用数据检验所选择概率分布的正确性。对于统计量连续分布的情况，可以采用点估计法、直方图法和概率图法确定随机变量的概率分布类型。

（2）参数估计。初步确定概率分布类型后，需要确定出该分布的参数，常用的参数估计方法为矩估计法和极大似然估计法。

（3）拟合优度检验。选择参数分布类型，并估计具体参数后，应当进行分布的拟合优度检验，即检验所选择的具体分布是否符合给定的数据分布。拟合优度检验是一种统计假设检验，用于检验观测样本是否服从于概率分布函数的理论分布。常用的拟合检验方法包括检验法和Kolmogorov-Smirnov检验法。

1.2 仿真调度机制

蒙特卡洛仿真通常需要将一个仿真任务执行成千上万次，要耗费大量的时间，使得系统设计周期过长，因此并行计算是进行蒙特卡洛仿真的一个必然选择。Matlab的分布计算工具箱提供了利用计算机集群进行并行计算的功能。

分布计算工具箱通过MATLAB分布式计算引擎可支持开发能在多台计算机上运行的分布式MATLAB计算应用程序，无需改换原有的MATLAB开发环境。用户可先在MATLAB中完成计算程序的开发与调试，然后利用该工具箱将算法分解为多个相互独立或相关的任务。MATLAB分布式计算引擎在多个远程MATLAB进程中同步调度和处理这些任务，相比单一的MATLAB进程执行，运行时间大大缩短。

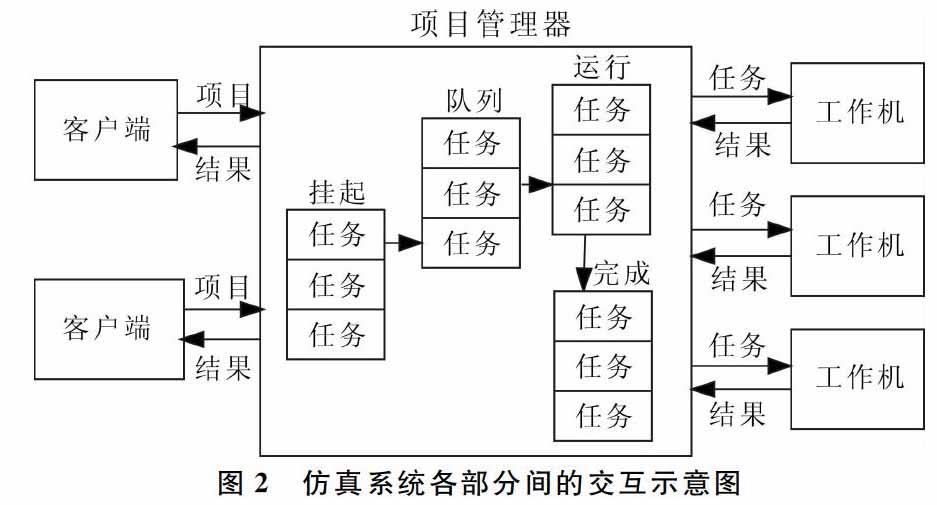
MATLAB分布计算工具，仿真系统由以下部分组成：①客户端：定义项目，将项目分解成多个任务，是用于进行MATLAB编程的计算机；②项目管理器：负责项目管理和任务分发，用户可以通过项目管理器将项目提交到项目队列以及将任务分发到工作机；③工作机：工作机接收项目管理器分配的任务，并进行计算。仿真系统各部分之间的交互如图2所示。

Matlab分布计算工具应用分为分布式执行以及并行计算，在应用分布计算工具进行蒙特卡洛仿真时，蒙特卡洛仿真作为用户提交的项目，可以自然地分为各个单次仿真任务，各单次仿真相互独立，因此属于分布式执行。

1.3 蒙特卡洛分析方法

对控制系统进行蒙特卡洛仿真本身不是目的，蒙特卡洛方法中重要的是应对蒙特卡洛仿真的结果进行充分有效的分析，使其能更好地服务于控制系统的设计及性能优化。对控制系统可以开展以下几方面的蒙特卡洛仿真分析。

（1）概率统计。首先确定任务成功的准则，然后通过蒙特卡洛仿真可以得到任务成功概率，能够直接对控制系统的性能进行评价。

（2）仿真模型验证。针对仿真模型中的某些错误和缺陷，单次仿真通常难以发现。因此对控制系统仿真模型，加入随机扰动及随机初始状态，进行蒙特卡洛仿真。在进行系统验证时，为充分暴露仿真系统的缺陷，设定的随机扰动的幅值可大于正常扰动幅值。通过对仿真统计结果和失败案例的概率分析，找出仿真系统的设计缺陷。

（3）控制系统灵敏度分析。采用灵敏度分析技术，确定特定输出与随机输入变量之间的灵敏度。采用最小二乘估计回归建立线性模型，使用多重测量的相关系数评估灵敏度。采用线性回归方法搜索仿真输入空间，找出对仿真输出影响最大的变量。

（4）定量的系统鲁棒性分析。采用蒙特卡洛方法计算系统的随机鲁棒性，得到定量的稳定性描述。

（5）控制器参数优化。在参数最优化计算中，当目标函数为非线性、存在多峰值或维数较高时，往往受到限制。这时应用蒙特卡洛方法比较有效，包括随机模拟算法，序贯随机模拟算法及随机搜索法等[6]。

（6）系统稳定性及飞行品质分析。对于电传飞控系统，通常考核它的动态特性和飞行品质，即输入驾驶员杆指令，考察时间响应、短周期阻尼、CAP、延迟时间等品质指标。

通过蒙特卡洛仿真，可获得阶跃响应时间常数、稳态误差、周期阻尼、CAP、延迟时间等指标的散布点，计算各品质指标的数学期望、方差，可获得飞行品质的概率估计值。

2 控制系统蒙特卡洛仿真方案

本文建立一种基于MATLAB分布计算工具的蒙特卡洛仿真系统，主要由客户端以及分布式计算机网络构成，仿真系统逻辑结构如图3所示。

2.1 客户端

客户端需安装并启用分布式计算引擎服务，并安装MATLAB 分布计算工具箱，用于创建分布式仿真作业。用户在客户端计算机的Matlab中构建Matlab仿真模型，创建蒙特卡洛仿真作业，并将作业提交给项目管理器，由分布式计算网络进行并行的仿真计算。客户端工作流程如图4所示。

最终的系统仿真结果会返回到客户端，因此蒙特卡洛分析工作也在客户端计算机进行。

2.2 分布式计算网络

分布式计算网络中由仿真管理节点和若干仿真节点组成。 该网络中的计算机都需要安装并启用MATLAB分布式计算引擎服务，管理节点运行作业管理器进程，仿真节点运行工作机进程。仿真管理节点负责仿真调度，它接收客户端提交的作业，将作业所包含的仿真任务自动分配到各个仿真节点进行计算，收集各工作机的计算结果。所有任务完成后将仿真结果返回到客户端。分布计算网络环境下的蒙特卡洛仿真整体工作流程如图5所示。

3 结语

可知蒙特卡洛方法本质上是一种基于参数随机抽样的数值计算方法，通过这种方法得出的结果可信度基于两个条件：①应建立可靠的数学模型，并将此数学模型与实际数据进行检验，尽可能在不使模型过于复杂的情况下令模型符合实际数据；②对模型中的随机量分布有明确的了解，进而针对不同的分布采取合理的随机抽样方法。此外，如果条件许可，应该对计算得出的统计结果与实际对照。

蒙特卡洛方法由于能够验证复杂系统的环境变化、子系统、部件及全部参数同时变化下的系统特性，可以进行参数的遍历性试验，因此具有较高的可信度，目前在国内外航空航天领域获得广泛应用，尤其在新型号飞行器控制系统的研制过程中，成为一种有效的、必备的检测和验证工具。

参考文献：

[1]PEGGY S， WILLIAMS. A monte carlo dispersion analysis of the X-33 simulation software[Z].NASA Dryden Flight Research Center， AIAA，2001.

[2]JOHN T， BOSWORTH，SUSAN J STACHOWIAK.Real-time stability margin measurements for X-38 robustness analysis[Z].NASA Dryden Flight Research Center，2005.

[3]GERTJAN LOOYE， HANS-DIETER JOOS， DEHLIA WILLEMSEN.Application of an optimization-based design process for robust autoland control laws[Z].AIAA，2001.

[4]GHN， LOOYE，SANCHO，et al.Design of robust autoland control laws using mu-Synthesis[C].AIAA Guidance， Navigation， and Control Conference and Exhibit，2002.

[5]杨云，张平. 电传飞控系统的蒙特卡洛分析与设计[J]. 航空学报， 2008，（29）：18-23.

[6]卢燕，舒传模. 蒙特卡洛法在导弹末制导雷达对目标的位置捕获概率估计中的应用[J]. 战术导弹技术， 2005（1）：29-33.

（责任编辑：陈福时）