基于非支配排序遗传算法的目标分配算法

徐磊 杜思伟

摘要：解决指挥控制领域的目标分配问题，主要使用单目标函数优化分配模型的分配方法。这一类方法的缺点是在当前时间序列上只考虑单一目标对下属节点的分配，未综合全局考虑分配任务的效率。本文先描述了单目标函数优化分配算法的使用步骤，后分析了该算法应用于指挥控制系统目标分配研究的优劣。再此基础上，进一步利用NSGA-II算法提出快速非支配排序机制的多目标分配算法，快速逼近多目标分配问题的Pareto最优解。

关键词：指挥控制 目标分配 非支配排序遗传算法

中图分类号：TP18 文献标识码：A 文章编号：1007-9416（2016）07-0120-02

1 引言

随着指挥控制系统的发展，需要其具备同时对20批以上目标的分配能力，指挥控制系统需要根据各下属节点的能力及目标的综合态势确定较优的分配方案。因此，目标优化分配是指挥控制领域最具有研讨价值的问题。

目标优化分配是最具有代表性典型的非确定多项式问题。随着指挥控制系统下属任务处理节点与目标数目的增加，目标分配的可选方案随着指控系统下属任务节点及目标数量的增加而呈几何式阶梯增长。

当指控系统有2个下属节点，用以应对2批目标时，可行的分配方案有16种；当指控系统有4个下属节点，用以应对4批目标时，理论可行分配方案数上升到65536种；而当下属节点和目标数量再次翻倍之后，总分配方案数的数量级已过亿，在实际工程应用中不可能通过穷举的方式获得最优解。

目前，目标优化分配方法主要有基于单目标函数优化分配模型的分配方法，以及针对该类模型改良的快速分配方法，这两种分配方法本质上其实是一类方法，这一类方法的缺点是在当前时间序列上只考虑单一目标对下属节点的分配，完成分配后转入下一个单一目标的分配任务，此时下属节点的可分配资源已减少，未综合全局考虑分配任务的效率，因此该方法不是最优化的分配方法。

2 单目标函数优化分配算法

下面给出单目标函数优化分配模型进行分析，目标函数和限制条件见表达式（1）、（2）：

（1）

（2）

式中：N：指挥控制系统下属可处理目标的节点数量；

M：参与优化分配的目标数量；

：目标j的任务紧迫度；

：下属节点i对目标j的分配有利度；

：目标j是否分配给下属节点i的假定值，=1分配，=0不分配，该假定数受任务分配可行性判断结果限制。∈D，D= {|满足资源、时间和空间约束}。

公式（1）的物理含义是把目标分配给处理最有利的下属处理节点，任务紧迫度高的目标具有优先选择权。

针对以上单目标优化分配模型，本文根据工程经验提出以下快速分配方法，该方法结合一系列先行的选优工作，能在较短时间内获得较优的可行解。步骤如下：

Step1：如指挥控制系统的下属任务处理节点数量N，从任务列表中选取2N的目标参与分配，任务序列中的目标已进行了时间和空间约束条件判断，按照任务紧迫度排序。

Step2：任务序列表中排序靠前目标最先参加目标分配，当目标到达分配时空域远界后，对目标进行资源约束条件判断，若满足条件，优选处理节点中分配有利度最高的处理节点进行分配，完成一批目标的分配。

Step3：重复步骤2，直到所有下属处理节点均有目标。

Step4：等待空闲的处理节点，实施再次分配。

该分配算法的优点是无需叠代，可在较短时间内获得较优的可行解，分配结果可保证将目标分配给任务最有利的处理单元，且漏分数量最小。缺点是：只考虑了当前单一目标任务有利度对分配结果的影响，未综合考虑全局处理单元对多目标的分配可能。因此有必要在指挥控制系统目标分配起始时，就考虑全局多目标的优化分配方案，以获得更优的分配方案。

3 基于非支配排序遗传算法的多目标分配算法

为了获得指挥控制系统对于多目标的全局优化分配结果，尝试将利用解决多目标决策问题的思路来解决时序上的单目标优化分配问题。

多目标分配决策的难点在于，全局的分配有利度与各目标自身的分配结果是可能存在一定矛盾的。理论上不可能存在每个目标的自身的分配结果均是最优的全局最优情况，往往是采用某种确定的分配方案后，会使目标域中的某一批目标的分配有利度变差。但由于该目标的牺牲，提升了全局的分配结果。基于以上的特征，可以规避使所有目标均达到最优分配的情况，转而在各目标之间进行协调，促使全域的分配结果尽可能的优化。

一般而言，根据各参考文献，利用解决多目标决策问题的思路来解决时序上的单目标优化分配问题的基本算法有线性加权求和法、密切值法、分层评价法等。以上算法的基本思路均是通过不同的数值计算方法，将多目标的全局有利度归化成单一值，用以衡量分配方案的优劣。这种做法的优点在于简单、快速、可实现性强，缺点在于计算效率低、算法鲁棒性及适应性差，在实际的工程实现中效果一般。

本文采用非支配排序遗传算法解决指挥控制系统的多目标分配问题。

3.1 遗传算法

遗传算法（Genetic Algorithm）是一类借鉴生物界适者生存、优胜劣汰遗传机制的进化规律演化而来的随机化搜索方法，其主要基于群体搜索策略在处理的群体间根据预先设定的模型进行信息的传递与交换。与牛顿梯度法等最优化算法的确定性、方向性搜索策略相比，遗传算法的处理机制是基于概率的，因此，其在处理和搜索最优解的过程中搜索到局部最优解的概率相对较低。另外，该算法的处理方式是非线程的，搜索过程不仅仅局限于单值解，因此，该算法比较适合于结果指控领域中的目标分配问题。

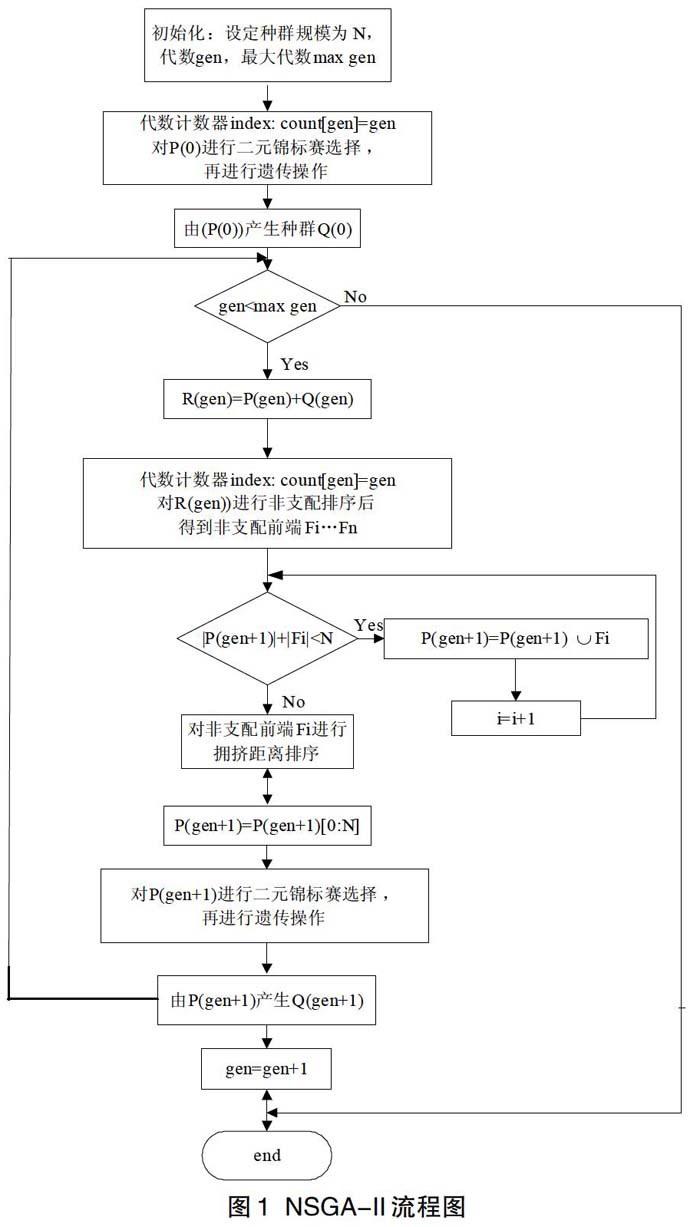
3.2 第二代非支配排序遗传算法（NSGA-II）描述

第二代非支配排序遗传算法（NSGA-II）是基于第一代非支配排序遗传算法NSGA的改进算法。

该算法采用了快速非支配排序（Fast Non-Dominated Sorting），采用了拥挤度及其比较算子，代替了第一代算法中需要使用者指定的共享半径。当排序过程中出现同级个体时，使用拥挤度及其比较算子作为次级排序的依据，从而保持了种群的多样性；另外，该算法在原算法的基础之上引入精英策略。该策略可以使得采样空间扩大，防止错失最优解，提高了算法的快速性和鲁棒性。

3.3 算法操作

步骤1 初始化：根据指控系统下属节点数量以及当前目标批数，初始化产生200组原始分配组合种群P0。对初始种群P0实施非支配倒序排序，排序完成后，按排序结果，对每一组分配方案赋一个非支配值R。

步骤2 选择：对初始化产生200组原始分配组合种群P0进行淘汰赛选择，即随机对200组原始分配组合进行两两配对，对于一对中的两组分配组合方式进行非支配值R的比较。假定参与比较的两对分配组合方式为A和B，其对应的非支配分别为RA和RB。根据预设原则“保留非支配大的那组分配组合方式，淘汰另一组分配方式” ，若RA

步骤3 交叉：选择后的分配组合种群P1中共有100组分配组合，该分配组合包括了指控下属任务节点的编号以及目标的批号。将目标的批号设定为单点交叉源，按照步骤2中的配对方式，对100组分配组合进行两两配对。对配对后的分配组合的目标批号进行相互交叉，形成交叉后的分配组合种群P2。

步骤4 变异：交叉后的分配组合种群P2中共有100组分配组合，该分配组合包括了指控下属任务节点的编号以及交叉后的目标批号。对于指控系统的目标分配问题，本文的变异操作采用下属节点与待分配目标的双元素变异。即使用一个新的指控下属节点或新的目标批号去替换原始分配组合中的某个组合，从而形成一个新的分配组合种群P3。具体的变异步骤如下：

（1）根据交叉后分配组合种群P2的规模大小，设定变异概率Pm，并确定变异门限g。随P2的规模增大或变异概率Pm的增大，变异的分配组合数量也会随之增大。

（2）对于交叉后分配组合种群P2中的每一组分配组合，产生一个[0，1]之间遵循高斯分布的随机数，若>g，则该分配组合需要进行变异操作。

（3）随机在全局可分配组合中挑选可用的指控下属节点或目标批号，对确定发生变异操作的分配组合的下属节点或目标批号进行更改。

算法流程如下图1所示。

4 结语

本文由浅入深，先描述了单目标函数优化分配算法的使用步骤，后分析了该算法应用于指挥控制系统目标分配研究的优劣；再此基础上，进一步利用NSGA-II算法提出快速非支配排序机制的多目标分配算法，快速逼近多目标分配问题的Pareto最优解，用于指挥控制系统的多目标分配研究。为指挥控制系统的多目标分配研究提供了一种可行、高效的解决方案。

参考文献

[1]邢清华，王颖龙，刘付显.多型号武器的目标优化分配问题研究[J].空军工程大学学报，2003，4（1）：22-25.

[2]王士同，刘征.动态武器目标分配问题的DWTA-GA算法[J].华东船舶工业学院学报，1999，13（5）：17-22.

[3]J.F.Aguilar Madeira，H.Rodrigues，Heitor Pina.Multi—objective optimization of structures topology bygenetic algorithms[J].Advances in Engineering Softwal'e，2005（36）：21-28.

[4]戴耀，汪德虎.舰艇火力分配的多指标模糊优选动态规划[J].辽宁工程技术大学学报，2001，20（5）：673-675.

[5]刘军，贾宏慧.基于改进的排列法的目标威胁评估与排序模型[J].计算机工程与设计，2007，28（19）：4750-4751.