创新教学模式，搭建自由平台

王高明

高中数学当中的研究性学习，指的是学生在教师的启发与指导下，从基础知识之外或是实际生活当中寻找数学研究课题，运用所学知识方法对之进行自由探究的教学活动.对于高中数学教学来讲，研究性学习是对于基础教学的拓展延伸，也是学生们学习效果升华的关键步骤.从形式上来看，研究活动的自由方式为学生们提供了广阔的发挥空间，有助于激发其自主学习的热情.从内容上来看，研究内容总是基于教材而又高于教材，能够有效打开学生视野，深化知识理解.

一、优化开端，在课堂教学中渗透研究性学习

研究性学习从表面看来虽然是一个“点”状的教学动作，它对数学教学所产生的影响却是呈现出“线”型的过程分布的.因此，对于研究性学习的落实绝不是一蹴而就的，它需要在整个教学过程中得到渗透与强调.在实际教学当中，作者从课程开端处便会开始进行优化，将课程导入的形式与内容向着研究性学习的模式去靠拢.

例如，在对等差数列前n项和的内容进行教学时，我先向学生们提出了三个问题：（1）求前100个自然数之和：1+2+3+…+100=？（2）求前n个奇数之和：1+3+5+…+（2n-1）=？（3）求前n个偶数之和：2+4+6+…+2n=？对于第一个问题，学生们还可以靠自己的计算知识勉强予以解答，而对于后两个问题，便需要大家展开思考，从中寻找到一些计算规律了.在对这个内容进行思考的过程中，等差数列前n项和的逻辑已经初露端倪了，这也是研究性学习思维的初步渗透.

高中数学当中的研究性学习是灵活、自由、实际的.这些特点也为课程开端处的优化处理提供了方向.在每一次主体教学展开之前，教师们都应当将本次内容进行一个“软化”处理，找到其中可以灵活拓展或是能与实际生活取得联系的部分，并将之以自然化、情境式的方式展现出来，让学生们从一开始便以研究性的思维走进知识.

二、强化过程，在开放问题中开展研究性学习

课堂教学当中的主体部分，除了是知识内容深入展开的重要阶段，也是研究性学习有效铺开的关键时段.作为对于基本内容的延伸与拓展，研究性学习是与基本知识的教学同步存在的.通过强化主体教学过程，研究性学习的开展效果也得以优化提升.谈及具体的强化方法，笔者认为，开放性问题的引入至关重要.

例如，在对等比数列的内容进行教学时，为了能够将学生们的思路最大限度地打开，我在课堂当中设置了这样一个开放问题：设等比数列{an}的公比为q，前n项和为Sn，是否存在一个常数c，使得数列{Sn+c}也成等比数列？若存在，求出这个常数c；若不存在，请说明理由.这个问题的出现，让学生们的思维顺利走出了基本知识形式的禁锢.这之中的字母常数也让问题的推导更具普遍性和灵活性.在这个自由探究的过程中，学生们对等比数列知识的理解更加深入了，并从中发现了问题，促进了自己的进一步研究.

从特点上来看，开放性问题与研究性学习之间存在很多相通之处.二者都是对基础知识内容的灵活拓展，需要学生们的自由探究，从而实现思想方法的实际运用与有效升华.因此，在研究性学习的主体呈现阶段加入开放性问题，对于激发学生思考热情和深化方法理解来讲颇有助益.开放性问题虽然比较灵活，但内容上仍然是以基本知识为出发点的，教师们在具体设计时也不会产生太大困难.

三、延伸教学，在生活实践中拓展研究性学习

研究性学习是一个长线的过程，并不随着课堂教学的结束而结束.将理论知识运用到实际问题的处理解决当中，一直是研究性学习的一个重要目标.因此，就将研究性学习的触角延伸至实际生活当中也就势在必行了.以生活实践为背景搭建数学研究平台，是研究性学习广泛开展的理想思路.

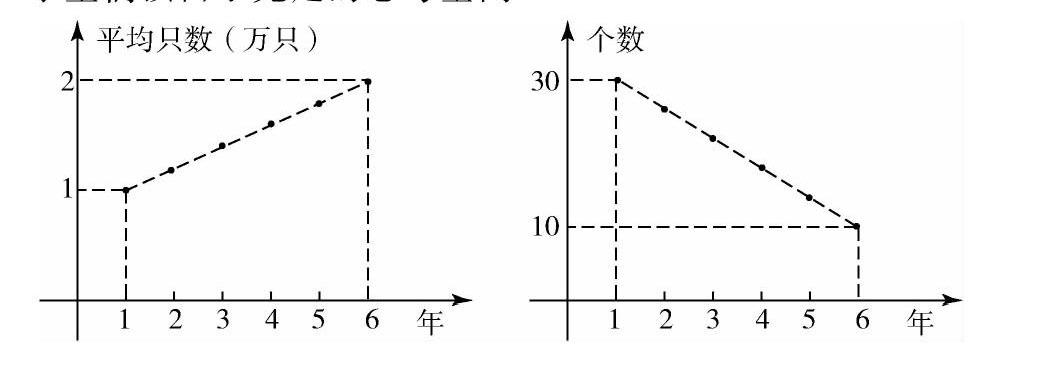
例如，在带领学生们学习了数列的知识内容后，我为学生们设计了这样一个应用问题：某人对当地养鸡场连续六年中的规模状况进行调研，得到如下两个图像.左图表示从第1年开始，每个养鸡场出产1万只鸡上升到第6年每个养鸡场出产2万只鸡.右图表示从第1年养鸡场个数30个减少到第6年10个.请从中求出第2年的养鸡场个数及所有养鸡场出产鸡的总只数，并分析出哪一年的养鸡场规模最大.这个问题的解答，对学生们的基本知识掌握以及运用图像进行灵活探究的能力要求很高.研究性的提问方式也为学生们预留了充足的思考空间.

对于理论教学的巧妙延伸，不仅达成了研究性学习的过程性目标，还很好地将学生们对于数学知识的思考与领悟带到了实际生活当中.这在促进学生加强对于生活的关注热度的同时，也让枯燥的理论知识在灵动生活的衬托之下变得越发有趣了.让每名学生都能够在积极的心态之中实现对高中数学知识内容的深入理解，是我们希望看到的.

从上文的论述不难发现，研究性学习对于高中数学教学来讲，是基于自由平台搭建之上的教学模式创新.它打破了传统固化的教学流程，走出了教材之内的基础内容限制，对既有知识进行拓展，并允许学生按照自己的思路对之进行讨论和探究，真正实现了思想方法的活学活用，完成了数学教学效果的升华.通过开端处的意识渗透、过程中的重点加强与课堂外的实践跟进，研究性学习得到了有效开展.这是新的时代背景对高中数学教学提出的新要求，也是教学活动迈向新高度的必经之路.