转换思维数学课堂教学的多维度思考与实践オ

张建军�オ�

身为高中数学教师，在尽力完成好每一次教学活动的同时，也在不断寻找着完善与提升教学实效的方式与方法.纵观当前常用的课堂教学模式，已经被教师们探究得比较深入了，在实践当中也能够将其精髓发挥出来.因此，想要进一步推进数学教学的顺利开展，在完善当前行动的基础上，更重要的是创新，转换思维，另辟蹊径，找到一个教学设计的新方向，在这个领域中继续寻觅，为高中数学教学注入新鲜血液.笔者结合当下的教学现状，从中分析出了一些薄弱之处，以此为据，从如下几个角度进行了教学方法完善，并在实践当中收获了较为理想的效果.

一、讲数学，同时讲文化，注重前期知识渗透

从教学环节上来讲，每一次新知识的引入，都需要经过一个课程导入的过程.这个过程，不仅能够从心理上将学生们的注意力由课下引导至课上，还能够为主体知识内容的出现打开一个入口，让学生们得以循序渐进地接受知识.在课程导入环节，教师们比较常用的方式包括提问、游戏、情境创设等等.笔者经过多次实践发现，在新课程开始之初以背景文化性内容开篇，同样能够达到很好的导入效果.

例如，在开始对解析几何的内容进行教学之前，我先向学生们介绍了一个相关的数学文化知识：在“数”与“形”之间建立起联系的历史上，笛卡尔是一个不得不提的功臣.他早在17世纪时，便发明了平面直角坐标系，并借助这个工具，成功实现了运用平面上的点来表示数，找到了点与数之间的一一对应关系.在这个基础之上，平面上的图形也得以通过数字予以表现.以前的方程学习经验，让大家掌握了用坐标系来表示直线的方法.其实，曲线也可以以点和数字来表示.在这样的介绍与启发之下，学生们很快走进了数形结合的思维之中，并对曲线的学习充满了期待.

在很多人眼中，数学都只是单纯的推导和计算，毫无文化可言，实则不然.数学是一门历史悠久的学科，它的发展过程构成了学科深厚的文化积淀.这种文化，不仅是这门学科的骄傲，更是推进数学研究的启发与动力.对数学文化进行了解与掌握，是高中数学教学的一个必要内容，却常常被教师们所忽略.用数学文化作为导入方式，在将学生们的思维引入课堂的过程中效果很好.

二、讲数学，同时讲技术，注重中期内容呈现

在很多情况下，仅靠教师一方的能力，很难将最为完整和生动的数学呈现在学生面前.特别是对于高中数学当中较为抽象的内容来讲，单一的语言叙述总是显得有些单薄，教师们需要寻找新的方式加以辅助.在这些辅助手段之中，现代信息技术手段经常会成为笔者的首选.随着时代与科技的发展，越来越多的技术手段得以应用于数学教学过程当中，它们也着实能够产生理想的效果.

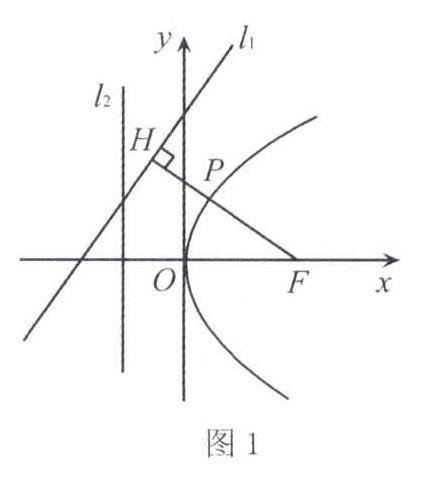
例如，在学习过抛物线的知识后，我请学生们尝试解答这样一个问题：现有直线l1：4x-3y+6=0，l2：x=-1，且点P是抛物线y2=4x上的一个动点.那么，该动点P到直线l1与直线l2的距离之和的最小值是多少？仅从字面上来看，学生们很难找到解答问题的切入点.即使将函数图象画出来，很多学生仍然不知道该如何放置点P.于是，我运用几何画板软件将已知条件当中的图形画了出来（如图1），并通过移动点P，让学生们在运动的过程中看到它到两条直线距离之和的变化规律.由此，大家非常直观地发现，当且仅当焦点F、动点P和直线FP与l1垂直时的垂足H共线时取得最小值，问题顺利得解.[TP9GS15.TIF，Y#]

现代信息技术手段在高中数学教学过程当中的应用点有很多，前文所述只是一个比较具有代表性的缩影.对于抽象性比较强，或是与图形之间具有紧密关联的知识内容，加入一定技术手段之后便能够将其更为生动灵活地展现出来.在这样的全新方式之下，学生们可以更加顺利和清晰地理解知识，并在体验演示的同时激活思维，一举两得.

三、讲数学，同时讲应用，注重后期方法理解

对于高中数学来讲，成功且完整的学习过程绝不是仅仅停留在理论层面上就止步了的.如果只懂理论，却不懂如何运用这些理论解决实际问题，便成了“光说不练假把式”.只有在与实践结合起来之后，才能说是将理论知识学懂学透了.知识应用于数学学习，既是一种检验学习效果的重要途径，更是全面掌握知识的必然要求.因此，在教学方式转变创新中，在讲理论的同时讲应用，应当成为教师们开展思考的一个关键课题.

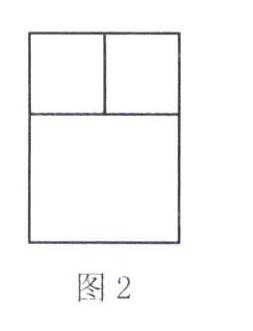
例如，在带领学生们学习过函数的内容后，我为大家设置了一道课后习题：某人想要用一根长6米的木料做一个如图2形状的窗框.在该窗框中，上、下框架的高度之比为1∶2.若想让光线通过窗框的面积达到最大，应该怎样对现有木料进行分配和使用呢？在这个问题的解答中，学生们很自然地运用到了方程的知识，并通过研究最大值的方式顺利得出了正确的设计方案.如果仅是让学生们面对方程内容本身进行练习，难免枯燥乏味.而在结合了实际生活当中的问题之后，大家的思考热情明显提升了.学以致用的过程，也让大家体味到了数学学习的乐趣.

可以看出，在理论知识的教授过程当中加入应用的元素，并不是一件困难的事情.数学本就是来源于生活，又回归于生活的，应用性是数学知识的一个附随特性.教师们在进行教学设计时，既可以考虑在课堂教学当中将理论与实践结合起来予以呈现，也可以在课后练习当中更多地设置一些实际应用问题，达到引导学生深入理解、灵活掌握的效果.有了实际生活的参与，数学在学生眼中也焕发出了生命力，大家的探究积极性越发高涨了.

从前文当中的叙述不难发现，高中数学教学方法的创新，需要教师们从两个角度完成思维转换：第一，立足教学方法本身，不断创新与灵动.高中阶段的知识内容本就枯燥抽象，难以引起学生们的关注热情.如果教师们继续一意孤行地停留在语言上的理论传授，只能让学生陷入被动学习与厌恶学习的恶性循环之中.新的教学方式的出现，无疑让学生眼前一亮，对于课堂教学的兴趣也就自然而然地迁移到知识内容上了.第二，实现不同教学方法与内容的巧妙整合.再精妙的教学方式，很多时候也难以让整次课堂教学充实起来.加之高中数学知识内容的综合性特点，需要教师们将相关内容结合起来，以多种形式予以呈现，方能实现“一次教学，多种收获”的优质效果.教师们的有效思维转换，必将为高中数学教学优化提供根本动力.