Plane Symmetric Solutions in f(R,T)Gravity

M.Farasat Shamir

Department of Sciences and Humanities,National University of Computer and Emerging Sciences,Lahore Campus,Pakistan

1 Introduction

The most popular issue in the modern day cosmology is the current expansion of universe.Observational and theoretical facts indicate that our universe is in the phase of accelerated expansion.[1]The existence of dark matter and dark energy is another interesting topic of discussion.[2]Almost a century ago,Einstein introduced the concept of dark energy by adding a small positive cosmological constant in the field equations.But he rejected this idea later on.However,it is now thought that the cosmological constant may become a suitable candidate for dark energy.Modified theories of gravity seem attractive to explain late time acceleration of the universe.An interesting modified theory of gravity is the f(R)theory which involves a generic function of Ricci scalar in standard Einstein–Hilbert Lagrangian.

In recent years,f(R)gravity has been investigated by many authors in different contexts.[3−17]Some interesting review articles[18]can be helpful to understand the theory.Bamba et al.[19]discussed curvature singularity appearing in the collapse process of a star in this theory.They proved that curvature singularity could be avoided by adding Rαterm in the viable f(R)gravity models.Thermodynamics of the apparent horizon in the Palatini f(R)gravity has been discussed by Bamba and Geng.[20]Capozziello et al.[21]found spherically symmetric solutions in f(R)gravity via Noether symmetries.Cylindrically symmetric vacuum and non-vacuum solutions have also been explored in this theory.[22]Sharif and Shamir[23]investigated plane symmetric solutions in metric f(R)gravity.The same authors[24]obtained the solutions of Bianchi types I and V cosmologies for vacuum and non-vacuum cases.Kucukakca and Camci[25]investigated Palatini f(R)gravity using Noether gauge symmetry approach.For this purpose,they considered a flat Friedmann–Robertson–Walker(FRW)universe and it was shown that the resulting form of f(R)gravity model yielded a power law expansion for the scale factor of the universe.Conserved quantities in metric f(R)gravity using Noether symmetry approach have been calculated.[26]

Another modified theory named as f(R,T)gravity has been developed by Harko et al.[27]It is the generalization of f(R)gravity and based upon the coupling of matter and geometry.In this theory,gravitational Lagrangian involves an arbitrary function of the scalar curvature R and the trace of the energy momentum tensor T.The equations of motions after the addition of an appropriate function f(T)indicate the presence of an extra force acting on test particles.The investigation of perihelion shift of Mercury using f(R,T)gravity provide an upper limit on the magnitude of the extra acceleration in the solar system which indicates the presence of dark energy.[27]Thus the study of f(R,T)gravity models may also provide better results as compared to the predictions of standard theory of general relativity(GR).The action for f(R,T)theory of gravity is given by[27]

where g is the determinant of the metric tensor gµνand Lmis the usual matter Lagrangian.It would be worthwhile to mention that if we replace f(R,T)with f(R),we obtain the action for f(R)gravity and replacement of f(R,T)with R leads to the action of GR.The energy momentum tensor Tµνis defined as[28]

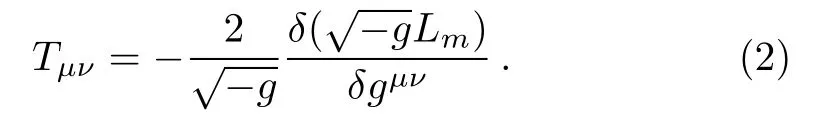
When we assume that the dependance of matter Lagrangian is merely on the metric tensor gµνrather than its derivatives,we get

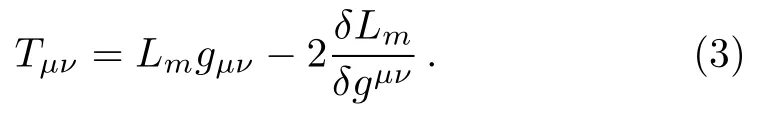
Many authors have investigated this theory in recent years and a reasonable amount of work has been done so far.

Adhav[29]explored the exact solutions of f(R,T) field equations for locally rotationally symmetric Bianchi type Ispacetime.Bianchi Type V cosmology with cosmological constant has been studied in this theory by Ahmed and Pradhan.[30]Jamil et al.[31]reconstructed cosmological models in f(R,T)gravity and it was concluded that the dust fluid reproduced ΛCDM,phantom-non-phantom era and the phantom cosmology.G¨odel type universe was studied in the framework of f(R,T)gravity by Santos.[32]Sharif and Zubair[33]discussed the reconstruction and stability of f(R,T)gravity with Ricci and modified Ricci dark energy.The same authors[34]analyzed the laws of thermodynamics in this theory.However,it has been proved that the first law of black bole thermodynamics is violated for f(R,T)gravity.[35]Houndjo[36]reconstructed f(R,T)gravity by taking f(R,T)=f1(R)+f2(T)where it was shown that f(R,T)gravity allowed transition of matter from dominated phase to an acceleration phase.Harko and Lake[37]found cylindrically symmetric interior string like solutions in f(R,Lm)theory of gravity.In a recent paper,[38]we investigated the exact solutions of cylindrically symmetric spacetime in f(R,T)gravity and recovered two solutions which corresponded to an exterior metric of cosmic string and a non-null electromagnetic field.We explored the exact solutions of locally rotationally symmetric Bianchi Type I universe in the context of f(R,T)gravity.[39]In another work,[40]we investigated Bianchi type I cosmology in f(R,T)gravity with some interesting results.It was concluded that equation of state parameter w→−1 as t→∞which suggested an accelerated expansion of the universe.Thus it is hoped that f(R,T)gravity may explain the resent phase of cosmic acceleration of our universe.This theory can be used to explore many issues and may provide some satisfactory results.

In this paper,we focus ourselves to investigate the exact solutions of plane symmetric spacetime in the framework of f(R,T)gravity.The plan of paper is as follows:In Sec.2,we give some basics of f(R,T)gravity.Section 3 provides the exact solutions for plane symmetric spacetime using two different classes of f(R,T)models.Summary and concluding remarks are given in the last section.

2 Some Basics off(R,T)Gravity

The f(R,T)gravity field equations are obtained by varying the action S in Eq.(1)with respect to the metric tensor gµν

where∇µdenotes the covariant derivative and

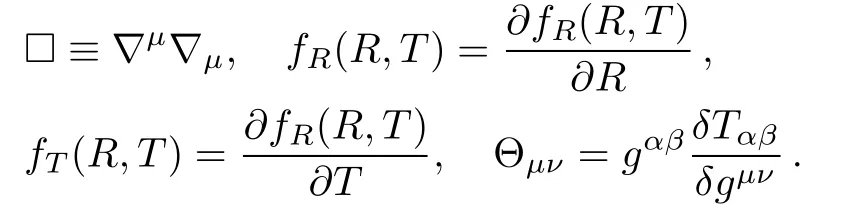
Contraction of Eq.(4)yields

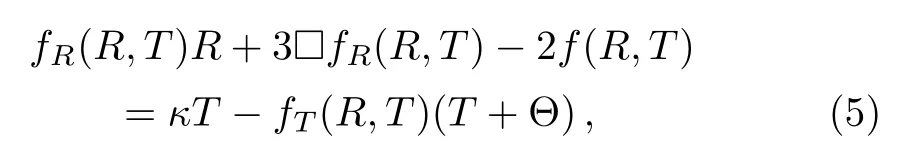
where Θ = Θµµ. This is an important equation because it provides a relationship between Ricci scalar R and the trace T of energy momentum tensor.Using matter Lagrangian Lm,Θµνand the standard matter energymomentum tensor are derived respectively as

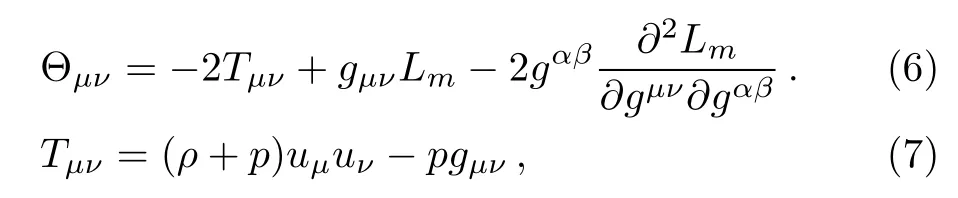
satisfying the equation of state

whereis the four-velocity in comoving coordinates and ρ and p denote energy density and pressure of the fluid respectively.Perfect fluids problems involving energy density and pressure are not any easy task to deal with.Moreover,there does not exist any unique definition for matter Lagrangian.Thus we can assume the matter Lagrangian as

Using this value in Eq.(3)and Eq.(7),we get a constraint equation

Similarly,using Eq.(6)and Eq.(9),we get

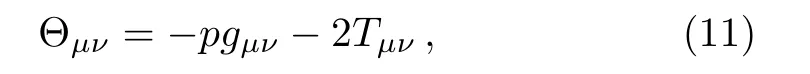
which gives an extra condition on p,

Using Eq.(11),the field equations(4)take the form

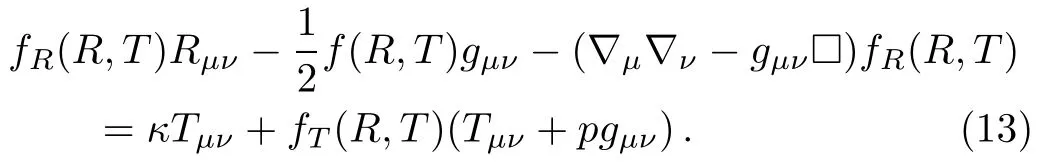
It is mentioned here that these field equations depend on the physical nature of matter field.Many theoretical models corresponding to different matter contributions for f(R,T)gravity are possible.However,Harko et al.[27]gave three classes of these models

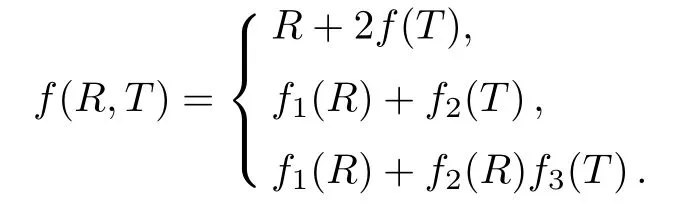
In this paper,we consider the first and second class only to investigate the exact plane symmetric solutions.

3 Exact Plane Symmetric Solutions

Here we shall find plane symmetric static solutions of the field equations in f(R,T)gravity.

3.1 Plane Symmetric Spacetimes

We consider the general static plane symmetric spacetime given by

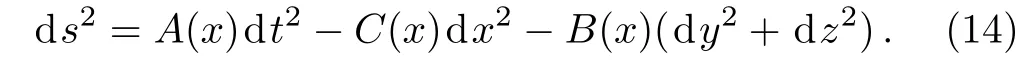
For the sake of simplicity,we choose C(x)=1 so that the above spacetime becomes

The corresponding Ricci scalar takes the form

where prime represents derivative with respect to x.Now,we explore the solutions of the field equations for two classes of f(R,T)models.

3.2 f(R,T)=R+2f(T)

For the model f(R,T)=R+2f(T),the field equations become

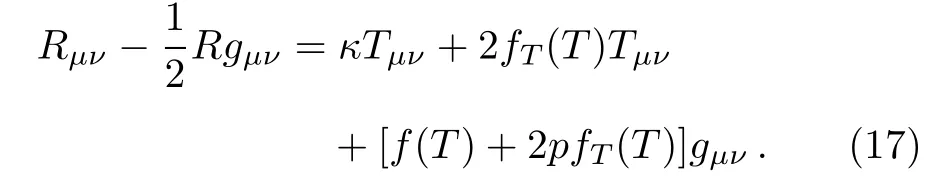
Here we find the most basic possible solution of this theory due to the complicated nature of field equations.However,in the next subsection we will explore the solutions with more general case.For the sake of simplicity,we use natural system of units(G=c=1)and f(T)= λT,where λ is a dynamical parameter.In this case,the gravitational field equations take the form similar to GR

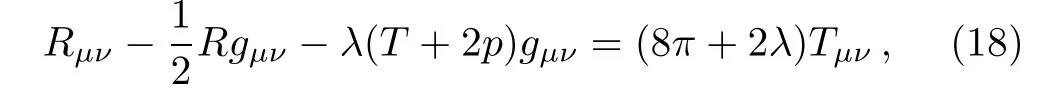
where the term λ(T+2p)may play the role of cosmological constant Λ of the GR field equations.It would be worthwhile to mention here that the dependence of the cosmological constant Λ on the trace of the energy momentum tensor T has already been proposed by Poplawski[41]where the cosmological constant in the gravitational Lagrangian is a function of T,and consequently the model was named as “Λ(T)gravity”.It was argued that recent cosmological data favour a variable cosmological constant which was consistent with Λ(T)gravity. Λ(T)gravity has been shown to be more general than the Palatini f(R)gravity.[42]

Now using Eq.(18),we obtain a set of differential equations for plane symmetric spacetime,

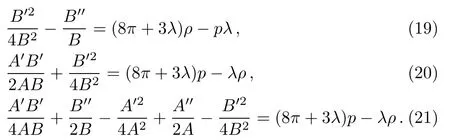
Thus we get three independent field equations in four unknowns namely A,B,ρ and p.Subtracting Eq.(20)and Eq.(21),it follows that

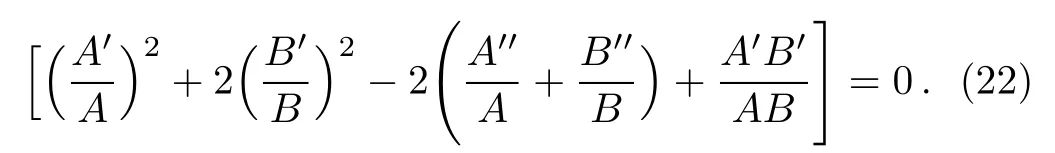
We solve this equation as follows:

Case I

As a first case,we solve Eq.(22)by the power law assumption,i.e.,A∝xrand B∝xl,where r and l are any real numbers.Thus we use A=k1xrand B=k2xl,where k1and k2are constants of proportionality.It follows that

and hence the solution metric becomes

It can be shown that these values of r and l lead to R=0.By substituting the solution A=k1x−2/3and B=k2x4/3back in Eqs.(19)–(21),we get either λ = −2π or λ = −4π which shows that λ is not an arbitrary constant.If were-define the parameters,i.e.,the above metric takes the form

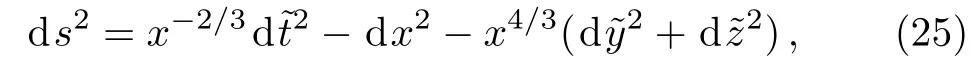
which is exactly the same as the well-known Taub’s metric.[43]

Case IINow we assume B=Anso that Eq.(22)gives

This equation yields a solution given by

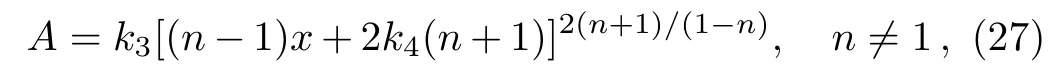
where k3and k4are integration constants.Without loss of generality,we can choose k3=1 and k4=0 so that Eq.(27)takes the form

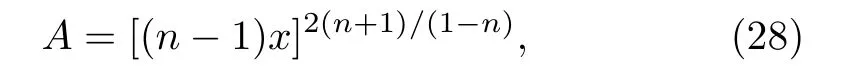
and thus B turns out to be

and the solution metric takes the form

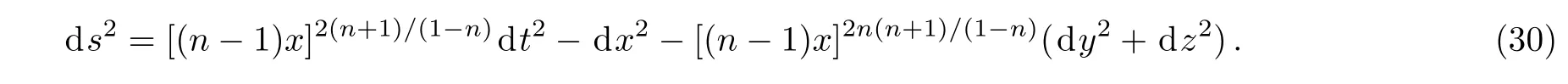
In this case,the energy density becomes

while the pressure of universe turns out to be

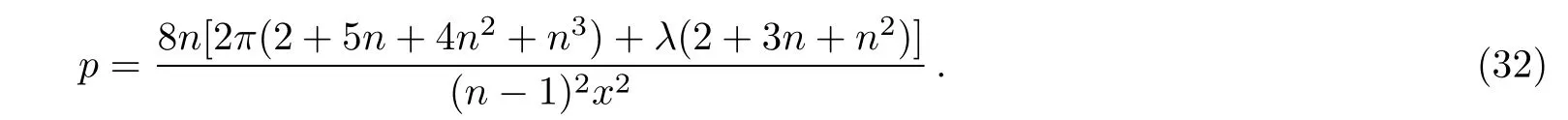
It would be worthwhile to mention here that we can recover Taub’s solution when n= −2.

3.3 f(R,T)=f1(R)+f2(T)

Now we explore the solutions with more general class.Here the field equations for the model f(R,T)=f1(R)+f2(T)become

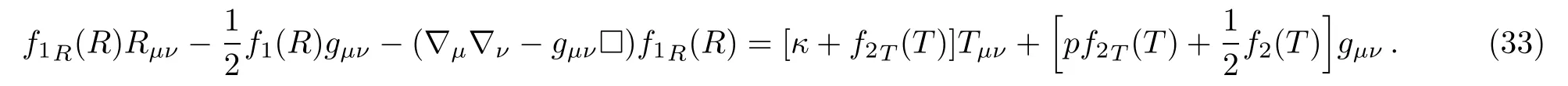
Contracting the field equations(33),we obtain

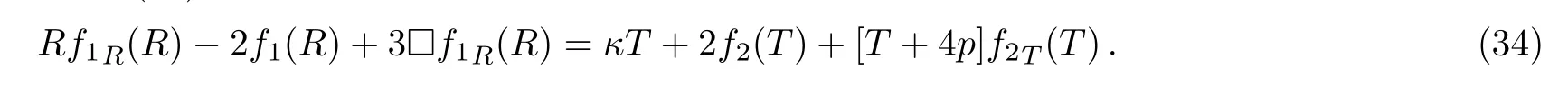
Using this,we can write

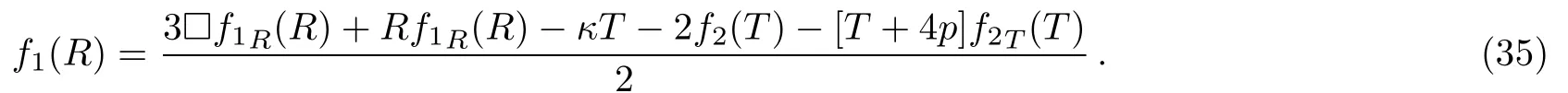
Inserting this in Eq.(33),we get

隔一年，我和妻子离婚了。妻子不愿意离婚，法官不愿意判决。我和妻子先后去法院纠缠半年多时间。我恳求法官看一下妻子膝盖和胳膊肘上的刀疤与鳞屑。我说，我担心哪一天妻子的刀片会划在我的脖子上。妻子坚持说，我这是刺血治疗皮肤病，我的心理没问题。我说，你的心理没问题，我的心理有问题，我跟你过日子早已失去了安全感。

Since the metric(15)depends only on x,one can view Eq.(36)as the set of differential equations for f1R(x),f2T(x),A and B.It follows from Eq.(36)that the combination

is independent of the indexµ and hence Aµ−Aν=0 for allµ and ν.Thus A0−A1=0 yields

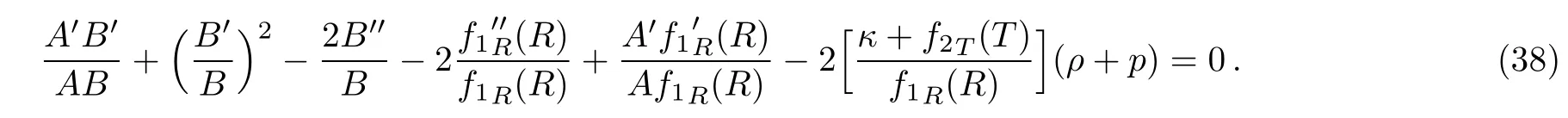
Also,A0−A2=0 provides

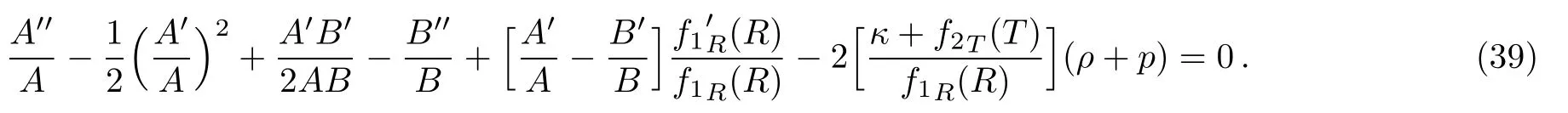
Thus we get two non-linear differential equations with fi ve unknowns namely A,B,f1R,f2T,ρ and p.The solution of these equations could not be found straightforwardly.Subtracting Eq.(38)and Eq.(39),we obtain

Due to highly non-linear nature of Eq.(40),here we also use the assumption B=An.Thus Eq.(40)reduces to

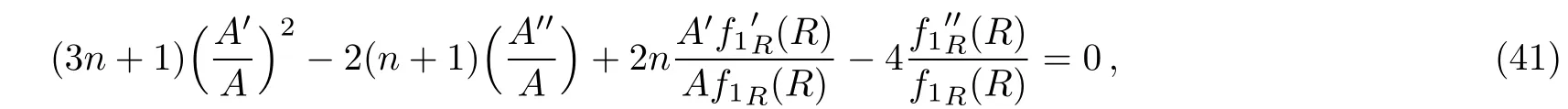
and the Ricci scalar turns out to be

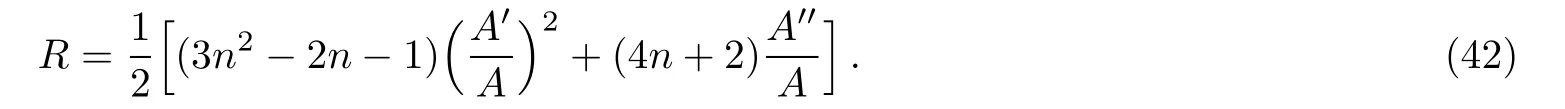
We follow the approach of Nojiri and Odintsov[44]and take the assumption f1R(R)∝f0Rm,where f0is an arbitrary constant.So using Eqs.(41),(42)and after some tedious calculations we obtain

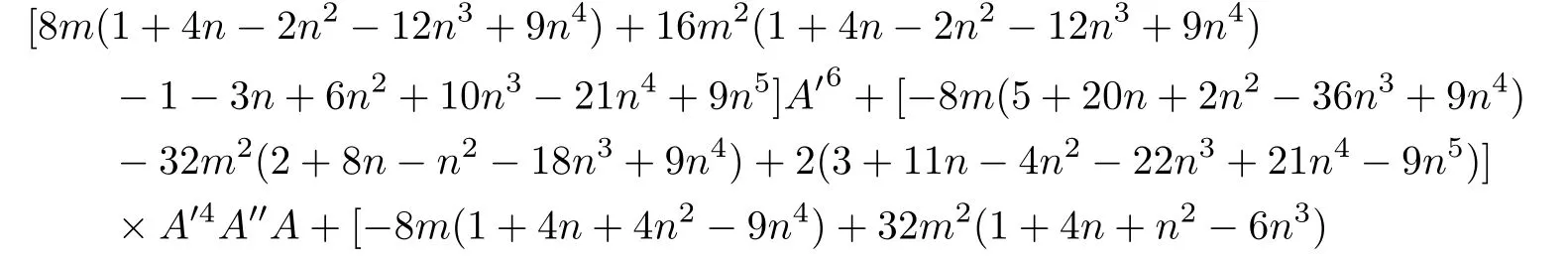
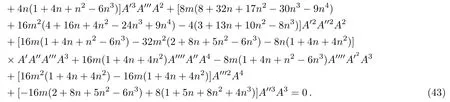
Case III

In this case we try to recover the Taub’s solution.For this purpose,we substitute A=x−2/3in Eq.(43).After some lengthy calculations,we obtain a constraint equation

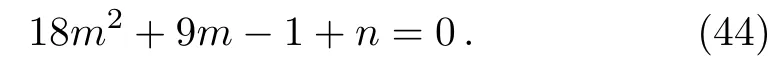
We can obtain B=x4/3for n=−2.Thus Eq.(44)reduces to

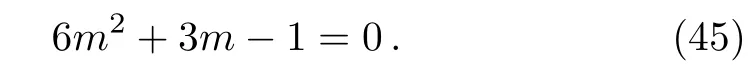
The roots of Eq.(45)turn out to be mThus,we have

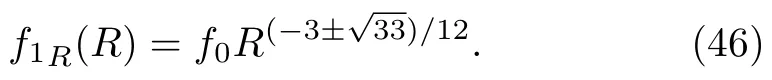
After integration,we obtain

whereand k5,k6are integration constants.It has been shown that the terms with positive powers of the curvature support the inflationary epoch.[45]The corresponding Ricci scalar is also zero in this case.Using first root mEoS parameter ω and Eqs.(38),(39),the energy density of the universe turns out to be

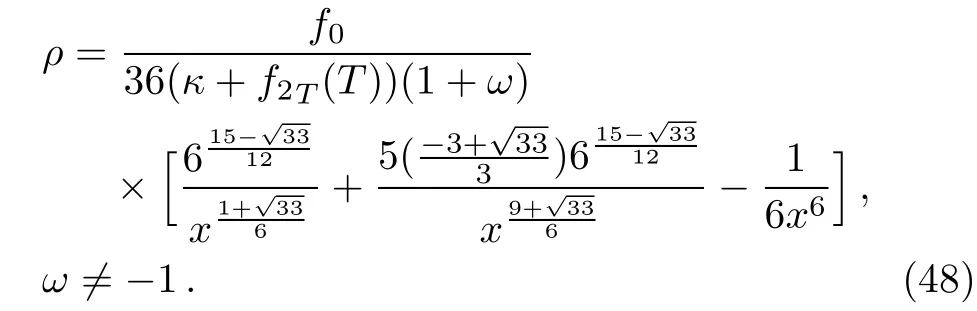
We can choose the sign of f0depending upon the values of ω to get the positive energy density.Similarly,we can find expression for energy density in the case of other root

Case IV

Here we take A=1/x in Eq.(43)to obtain a constraint equation

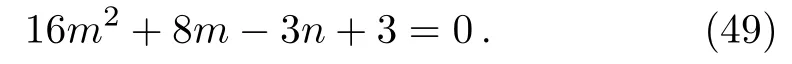
Using this equation,it follows that

The solution metric takes the form

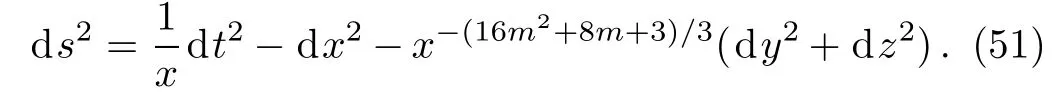
The corresponding Ricci scalar becomes

We can construct different f1(R)models for different values of m satisfying Eq.(49).However,an interesting logarithmic form of f1(R)models is obtained for m=−1

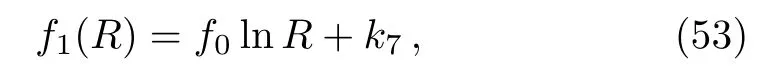
where k7is an integration constant.In this case Ricci scalar becomes R=98/3x2and the solution metric takes the form

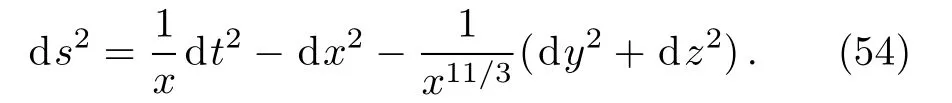
The matter density turns out to be

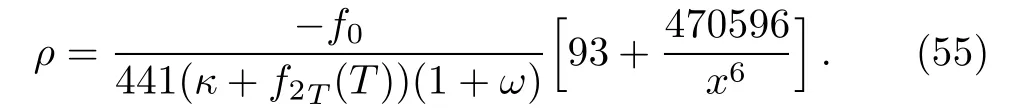
Similarly for m=−2,we obtain

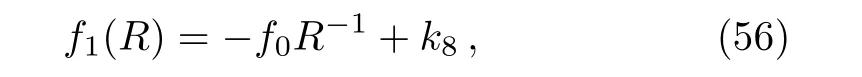
where k8is an integration constant.This model is also cosmologically important as it has been proved that negative power of curvature serves as an effective dark energy supporting the current cosmic acceleration.[45]Obviously one can work out the Ricci scalar,energy density and the solution metric in this case.

Case V

Here we consider A=eαx,where α is a non-zero real number.In this case,we obtain a constraint equation using Eq.(43)

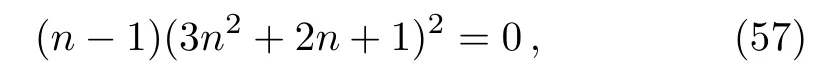
which does not involve parameter m.So this choice will yield a solution for any f1(R)model in power law or logarithmic form.The roots of Eq.(57)turn out to be

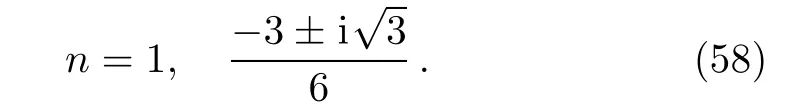
We discard the imaginary roots and consider the real value of n to get a physical solution.In this case the Ricci scalar turns out to be non-zero constant,i.e.,R=3.The energy density becomes

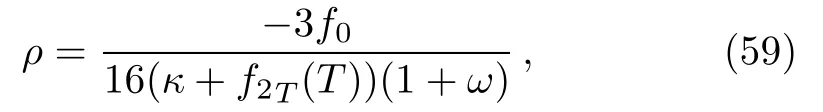
and the solution metric becomes

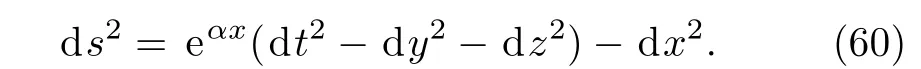
This corresponds to the well-known anti-deSitter spacetime in GR.[46]

3.4 Physical Importance of the Solutions

The spacetime admitting three parameter group of motions of the Euclidean plane is said to possess plane symmetry and is known as a plane symmetric spacetime.Such spacetime possesses many properties equivalent to those of spherical symmetry.The plane symmetric spacetime has been extensively investigated by many researchers from various standpoints.Taub,[47]Bondi,[48]Bondi and Pirani–Robinson[49]defined and studied plane wave solutions.They considered the concept of group of motions of spacetime which played a fundamental role in plane gravitational waves.It has been established that the spacetime Eq.(15)admits the plane wave solutions of GR field equations.[50]

In this study,we have explored plane symmetric solutions in the context of f(R,T)gravity.The non-vacuum plane symmetric solutions provide Taub’s universe with a singularity at x=0,which suggests the presence of black hole.Another solution(51)suggests that an object falling into a black hole approaches the singularity at x=0.However,non-singular solution is obtained in the shape of an anti-deSitter spacetime.An anti-deSitter space is a GR like spacetime,where in the absence of matter or energy,the curvature of spacetime is naturally hyperbolic.From geometrical point of view,an anti-de Sitter space has a curvature analogous to a flat cloth sitting on a saddle,with a very slight curvature because it is so large.Thus it would correspond to a negative cosmological constant.Anti-deSitter space can also be thought as empty space having negative energy,which causes this spacetime to collapse at a greater rate.The existence of quantum-corrected deSitter space has been predicted as an outcome of a nontrivial solution for constant curvature R0in f(R)gravity.[51]One may play with the parameters of the theory under consideration in such a way that the deSitter space can provide a solution to the cosmological constant problem.Thus the physical relevance of the solutions is obvious.

4 Concluding Remarks

This paper is devoted to explore the exact static plane symmetric solutions in f(R,T)gravity.To our knowledge,this is the first attempt to investigate plane symmetric solutions in f(R,T)gravity. In this work,we consider two classes of f(R,T)models.First we take f(R,T)=R+2f(T).For this class,we investigate two cases and recover a solution which corresponds to the well known Taub’s spacetime.[43]The expression for matter density ρ and pressure p have been calculated for this solution.

The second class with f(R,T)=f1(R)+f2(T)is the more general choice to explore the solutions.We assume f1R(R)∝f0Rm,where f0and m are arbitrary real constants.The corresponding field equations are solved for three cases,which provide one new solution and two important solutions namely Taub’s and anti-desitter spacetimes are recovered.So the physical relevance of these solutions is obvious.The function of Ricci scalar f1(R)contains positive power of curvature in the first case while the second case corresponds to negative power of curvature.It is worth mentioning here that the terms with positive power of curvature support the in flationary epoch while the term with negative power of curvature serve as an effective dark energy which supports the current cosmic acceleration.[45]We also provide a choice for solution with logarithmic form of f(R)model.

We have discussed five cases in this paper.However,many other cases can also be explored and different cosmologically important f(R,T)models can be reconstructed.It would be worthwhile to mention here that such solutions may provide a gateway towards the solution of dark energy and dark matter problems.It also seems interesting to explore the exact solutions in other modified theories of gravity.The investigation of plane symmetric solutions in f(G)gravity is under process.

Acknowledgments

The author would like to acknowledge National University of Computer and Emerging Sciences(NUCES)for funding support through research reward programme.The author is also thankful to the anonymous reviewer for valuable comments and suggestions to improve the paper.

References

[1]A.G.Riess,et al.,Astron.J.116(1998)1009;S.Perlmutter,et al.,Astrophys.J.517(1999)565;D.N.Spergel,et al.,Astrophys.J.Suppl.170(2007)377.

[2]S.Nojiri and S.D.Odintsov,Int.J.Geom.Meth.Mod.Phys.4(2007)115;M.S.Turner and D.Huterer,J.Phys.Soc.Jap.76(2007)111015;V.Sahni and A.Starobinsky,Int.J.Mod.Phys.D 9(2000)373;D.H.Weinberg,New.Astron.Rev.49(2005)337.

[3]M.Sharif and M.Zubair,Adv.High Energy Phys.2013(2013)790967.

[4]M.Sharif and H.R.Kausar,JCAP 07(2011)022.

[5]M.Sharif and H.R.Kausar,Int.J.Mod.Phys.D 20(2011)2239.

[6]M.Sharif and H.R.Kausar,Astrophys.Space Sci.331(2011)281.

[7]M.Sharif and H.R.Kausar,Mod.Phys.Lett.A 25(2010)3299.

[8]M.F.Shamir and Z.Raza,Commun.Theor.Phys.62(2014)348.

[9]K.Bamba,S.Nojiri,S.D.Odintsov,and D.Saez-Gomez,Phys.Lett.B 730(2014)136.

[10]K.Bamba,A.N.Makarenko,A.N.Myagky,S.Nojiri,and S.D.Odintsov,JCAP 01(2014)008.

[11]K.Bamba,S.Nojiri,and S.D.Odintsov,Phys.Lett.B 698(2011)451.

[12]S.Capozziello and S.Vignolo,Int.J.Geom.Meth.Mod.Phys.8(2011)167.

[13]S.Capozziello,F.Darabi,and D.Vernieri,Mod.Phys.Lett.A 26(2011)65.

[14]S.Capozziello,M.D.Laurentis,S.D.Odintsov,and A.Stabile,Phys.Rev.D 83(2011)064004.

[15]E.Elizalde,S.Nojiri,S.D.Odintsov,and D.Saez-Gomez,Eur.Phys.J.C 70(2010)351.

[16]K.Bamba,C.Geng,S.Nojiri,and S.D.Odintsov,Mod.Phys.Lett.A 25(2010)900.

[17]S.Capozziello,M.D.Laurentis,S.Nojiri,and S.D.Odintsov,Gen.Rel.Grav.41(2009)2313.

[18]A.D.Felice and S.Tsujikawa,Living Rev.Rel.13(2010)3;T.P.Sotiriou and V.Faraoni,Rev.Mod.Phys.82(2010)451;T.Clifton,P.G.Ferreira,A.Padilla,and C.Skordis,Phys.Rept.513(2012)1;S.Nojiri and S.D.Odintsov,Phys.Rep.505(2011)59;K.Bamba,S.Capozziello,S.Nojiri,and S.D.Odintsov,Astrophys.Space Sci.342(2012)155.

[19]K.Bamba,S.Nojiri,and S.D.Odintsov,Phys.Lett.B 698(2011)451.

[20]K.Bamba,and C.Geng,JCAP 06(2010)014.

[21]S.Capozziello,A.Stabile,and A.Troisi,Class.Quantum Grav.24(2007)2153.

[22]A.Azadi,D.Momeni,and M.Nouri-Zonoz,Phys.Lett.B 670(2008)210;M.Sharif and S.Arif,Astrophys.Space Sci.342(2012)237.

[23]M.Sharif and M.F.Shamir,Mod.Phys.Lett.A 25(2010)1281.

[24]M.Sharif and M.F.Shamir,Class.Quantum Grav.26(2009)235020;M.Sharif and M.F.Shamir,Gen.Relativ.Gravit.42(2010)2643.

[25]Y.Kucukakca and U.Camci,Astrophys.Space Sci.338(2012)211.

[26]M.F.Shamir,A.Jhangeer,and A.A.Bhatti,Chin.Phys.Lett.29(2012)080402.

[27]T.Harko,F.S.N.Lobo,S.Nojiri,and S.D.Odintsov,Phys.Rev.D 84(2011)024020.

[28]L.D.Landau and E.M.Lifshitz,The Classical Theory of Fileds,Butterworth-Heinemann(2002).

[29]K.S.Adhav,Astrophys.Space Sci.339(2012)365.

[30]R.L.Naidu,D.R.K.Reddy,T.Ramprasad,and K.V.Ramana,Astrophys.Space Sci.348(2013)247.

[31]M.Jamil,D.Momeni,M.Raza,and R.Myrzakulov,Eur.Phys.J.C 72(2012)1999.

[32]A.F.Santos,Mod.Phys.Lett.A 28(2013)1350141.

[33]M.Sharif and M.Zubair,Astrophys.Space Sci.349(2014)529.

[34]M.Sharif and M.Zubair,JCAP 03(2012)028.

[35]M.Jamil,D.Momeni,and R.Myrzakulov,Chin.Phys.Lett.29(2012)109801.

[36]M.J.S.Houndjo,Int.J.Mod.Phys.D 21(2012)1250003.[37]T.Harko and M.J.Lake,arXiv:1409.8454.

[38]M.F.Shamir and Z.Raza,Astrophys.Space Sci.356(2015)111.

[39]M.F.Shamir,Eur.Phys.J.C 75(2015)354.

[40]M.F.Shamir,J.Exp.Theor.Phys.146(2014)281.

[41]N.J.Poplawski,arXiv:gr-qc/0608031.

[42]N.J.Poplawski,Class.Quantum Grav.23(2006)4819.

[43]M.L.Bedran,M.O.Calvao,F.M.Paiva,and D.Soares,Phys.Rev.D 55(1997)6.

[44]S.Nojiri and S.D.Odintsov,Phys.Rep.505(2011)59.

[45]S.Nojiri and S.D.Odintsov,Phys.Rev.D 68(2003)123512.

[46]T.Feroze,A.Qadir,and M.Ziad,J.Math.Phys.42(2001)4947.

[47]A.H.Taub,Annals Math.53(1951)472.

[48]H.Bondi,Nature(London)179(1957)1072.

[49]H.Bondi,E.Pirani,and I.Robinson,Proc.Roy.Soc.251(1959)519.

[50]H.Takeno,Tensor(N.S.)7(1957)97.

[51]G.Cognola,E.Elizalde,S.Nojiri,et al.,JCAP 0502(2005)010.