基于变分辨率栅格模型的启发式有向搜索最优路径算法
华剑锋,张 丰,杜震洪*,刘仁义,李荣亚(1.浙江大学浙江省资源与环境信息系统重点实验室,浙江杭州310028;2.浙江大学地理信息科学研究所,浙江杭州310027)
基于变分辨率栅格模型的启发式有向搜索最优路径算法
华剑锋1,2,张 丰1,2,杜震洪1,2*,刘仁义1,2,李荣亚1,2
(1.浙江大学浙江省资源与环境信息系统重点实验室,浙江杭州310028;2.浙江大学地理信息科学研究所,浙江杭州310027)
摘 要:针对连续空间中无法直接采用图论方法进行路径分析的问题,提出了基于四叉树思想构建的变分辨栅格模型.该模型不仅兼顾了地形表达精度与数据冗余度,而且避免了地物“边缘效应”的影响.在该模型基础上,设计了一种启发式有向搜索算法,该算法在搜索节点时,首先对相邻节点进行方向性选择,减少搜索空间,提高了算法的效率.实验结果表明,提出的模型及算法不仅能够求得连续空间中的最优路径,而且具有较高的计算效率.
关 键 词:最优路径;连续空间;变分辨率;栅格模型;有向搜索方法
0 引 言
路径分析一直是各个学科研究的热点,也是GIS网络分析的基本问题,其核心是对最优路径的求解.由于GIS矢量数据表达的是一种离散空间,存在预定的节点及轨迹,因此可以很方便地将其抽象为具有节点和连线的网络,继而将问题转换为在图论意义下利用最短路径算法求解最优路径的问题.然而,GIS栅格数据表达的是一种连续空间,不存在预定的节点和轨迹,因而用于求解矢量数据最优路径的策略和算法并不适用于栅格数据.实际中也往往遇到此类问题,例如航空线路规划、输电线路选址、道路工程设计、森林火灾蔓延等.目前为止,国内外专家学者对基于矢量数据求解最优路径的研究较多,但对栅格数据求解最优路径策略和算法的相关研究较少,且多见于人工智能领域对移动机器人行走路径的求解[1-4],而在GIS领域鲜有文献报道.基于GIS栅格数据求解最优路径的关键在于栅格数据模型的构建策略,以及最优路径算法的设计与优化.
在栅格数据模型构建方面,文献[5]引入地表障碍距离构建了网格模型,该模型综合考虑地理空间高程、坡度、障碍物等因素的影响,易于实现路径的寻优计算.文献[6]利用网格划分栅格数据,结合点、边、属性等约束条件,以图或网络的方式描述栅格数据,最后在网络模型中求解最优路径.文献[7]将离散的矢量网络作为辅助,在连续的栅格表面描述道路网络,以此来求解栅格表面考虑地形要素的最优车辆出行线路.这些文献都对栅格数据进行了模型构建,也考虑了障碍物等因素的影响,但所构建的栅格模型均属于单分辨率模型,这种模型在解决实际问题时存在2个问题:(1)不能兼顾地形表达精度与数据冗余度.当分辨率过低时,不能精确表达地形复杂度,从而影响路径寻优计算的准确性;当分辨率过高时,虽能精确表达地形复杂度,但会造成数据的大量冗余,增加路径寻优的计算成本.(2)在路径规划时往往会遇到如图1所示的问题,图1中,PS为起点,PE为终点,A、B为路径规划区域内的面状地物(如居民区、自然保护区等),理想的路径应该为L1,但计算机在自动选线时往往会绕道而行选择类似L2的路径,这是由于地物虽然只覆盖了单元格的一部分,但单元格因为拥有了地物信息,导致计算机选线时绕道而行,这种现象称为地物的“边缘效应”.

图1 地物“边缘效应”Fig.1 Edge effect
在栅格数据最优路径算法方面,文献[8]在栅格数据环境下,采用Dijkstra算法,通过维护OPEN 和CLOSED表来进行节点的搜索,并构建了索引数组来判断待搜索的节点是在OPEN表还是在CLOSED表中,由此提高了算法的效率.但Dijkstra算法的优点在于能够计算起始节点到其他所有节点的最优路径,是一种发散式的搜索,并不适合给定起点和终点的最优路径问题.文献[9]采用A*算法计算最优的步行路径.A*算法是一种关注起点到终点的最优路径算法,同时也是一种人工智能算法,更适合在栅格数据中进行求解,但文献[9]并未对A*算法做任何改进,使得算法的效率较低.
为了解决上述模型和算法上的问题,本文提出变分辨率栅格数据模型,采用四叉树的思想将地形复杂区域或地物边缘进行不断细分,直至细分后的单元格具有唯一性质,而对地形平坦区域则保留初始的分辨率,从而,在兼顾地形表达的精度与数据冗余度的同时避免了地物“边缘效应”的影响.进而,在模型的基础上,设计启发式有向搜索算法,通过引入有向搜索方法,建立适当的筛选条件,避免对不必要节点的搜索,在节点搜索过程中进行方向性选择,缩小搜索范围,提高算法效率.
1 变分辨栅格数据模型
变分辨率栅格数据模型不同于单分辨率栅格数据模型,由相互邻接、分辨率不同的单元格构成,因而其实现原理、单元格的领域模式、单元格通行代价的计算方式也有所不同.
1.1 实现原理
变分辨率栅格数据模型基于四叉树的思想构建,它不断地将具有多重性质的单元格四分为大小相同的子单元格,直到所有的单元格都具有唯一的性质,从而使具有多重性质的单元格得到精细表达.而单一性质的单元格由于无须细分减少了数据存储量.图2是一个二值8*8的栅格模型及其对应的四叉树结构,首先将其细分为4个子域(NW、NE、SE、SW),然后继续细分子域直到每个子域都具有唯一值.

图2 栅格数据的四叉树结构Fig.2 The quad tree structure of raster data
在连续空间中进行最优路径分析需要考虑多种影响因素(如居民区、自然保护区、名胜古迹等),这些影响因素在最优路径分析中被作为障碍物.将连续空间以规则镶嵌的方式栅格化后,某些影响因素不会完全覆盖某些单元格,这种情况多发生于地形复杂的区域或地物的边缘,此时,就采用四叉树的方式对其进行细分,地形复杂区域或地物边缘由于被划分得更为细致,从而得到精细化的表达,同时也避免了地物的“边缘效应”.而对于地形平坦的区域或障碍物较少的区域,则不进行细分,这样的好处是减少了数据的存储总量,使得数据整体的冗余度较低.
1.2 单元格的领域模式
如同图3搜索中需要给定图的节点和连线,变分辨率栅格数据模型也需要指定单元格的领域模式.单分辨率栅格数据模型的领域模式通常有4,8,16,32等,而变分辨率栅格数据模型的领域模式则更为复杂,这是因为其指定单元格的相邻单元格个数是不确定的.本文采用判断单元格是否相邻的方法来确定指定单元格的领域模式,具体方法为将指定单元格的中心作为节点,搜索与它相邻的所有单元格,并将这些单元格作为指定单元格的领域模式,相邻单元格的节点称为相邻节点,指定节点与相邻节点之间的连线称为通行路径.
1.3 单元格的通行代价计算
在进行实际最优路径分析时,受地形地貌或者居民区、自然保护区等因素的影响,通过每一个单元格的代价都是不同的,因此,需对单元格的通行代价进行具体计算.本文依据单元格是否覆盖障碍物将其划分为障碍物单元格和可通行单元格,障碍物单元格不允许线路通过,而可通行单元格计算通行的代价通常考虑地形、坡度、距离等因素,各个因素的影响权值可以不同,单元格通行代价值Cost由式(1)计算得到.
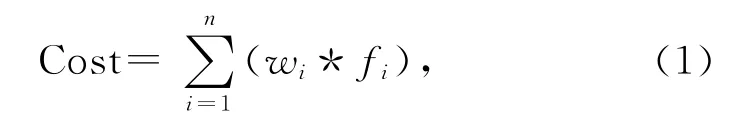
式中,i为影响因素编号,fi为编号为i的影响因素,wi为该影响因素的权值.
2 启发式有向搜索算法及分析
变分辨率栅格数据模型是最优路径分析的基础,它为最优路径分析提供了数据模型支持.同时,最优路径分析也离不开算法的支持.本文对A*算法进行改进,设计了启发式有向搜索算法.
2.1 启发函数的建立
A*算法在搜索过程中使用启发函数,对搜索的每一个节点进行代价评估,优先选择代价最小的节点,再从这个节点继续搜索,直到搜索到目标,从而省略了大量无谓的搜索路径,增强了搜索的目标性,提升了效率.其核心算法函数为f(x)=g(x)+h(x),其中g(x)为起点到该节点的实际最小代价,h(x)为该节点到终点的估算代价,f(x)即为从起点到终点并经过了该节点的最小代价.
2.2 有向搜索方法对A*算法的优化
为了进一步提高A*算法的搜索效率,本算法在搜索节点时,首先计算2个夹角值θ1和θ2,以判断待搜索的节点是否在当前节点和终点内.如图3所示,建立以当前节点为原点0,以原点0到终点1的连线方向为x轴的直角坐标系.θ1为待搜索节点2、原点0和终点1构成的夹角,θ2为待搜索节点2、终点1和原点0构成的夹角.当θ1、θ2同时满足小于等于90°时,才将其纳入当前节点的可扩展节点集.此项工作相当于对变分辨率栅格数据模型中各个节点的相邻节点进行数据预处理.
计算公式如下:
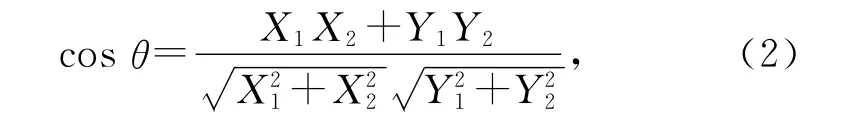
其中,(X1,Y1)和(X2,Y2)分别为同一直角坐标系中2个点的坐标,θ为两点与坐标原点间连线的夹角.

图3 有向搜索方法Fig.3 The method of directional algorithm
2.3 实现过程
设置节点的状态为{j,isObstacle,Cost,g(j),h(j),f(j),preNode},其中,j为当前节点标识;preNode为j的父节点,i为preNode的父节点标识;isObstacle为节点所在单元格的障碍标识,其取值为true或false,true值表示该单元格为障碍物单元格,false值表示该单元格为可通行状态;Cost为该单元格的通行代价;g(j)为从起点沿着产生的路径,移动到当前节点的实际代价,g(j)=preNode.g(j)+Cost;h(j)为当前节点移动到终点的估算代价,该值可以是曼哈顿距离、欧氏距离、切比雪夫距离,算法采用曼哈顿距离,即首先计算从当前节点移动到终点水平和垂直方向的各个分辨率的单元格的数量之和,再乘上单元格所代表的实际距离;f(j)=g(j)+h(j).
建立3个链表ORIGINAL、OPEN和CLOSED,ORIGINAL为“初始列表”,存放了所有单元格节点;OPEN为“开启列表”,用来存放所有待检查的节点;CLOSED为“关闭列表”,用来存放所有已访问过的节点,这些节点在后续的搜索中无须再次被检查.OPEN和CLOSED表的初始状态置为空.算法的具体步骤如下:
1)将所有节点的状态设置为{j,isObstacle,Cost,∞,h(j),∞,null}放入到ORIGINAL表中,将初始节点(即起点PS)的状态设置为{j,false,0,0,0,0,null},放入到OPEN表中.
2)在ORIGINAL表中搜索所有与起点PS相邻的节点,排除具有以下特征的节点:(1)θ1、θ2不满足条件;(2)isObstacle状态为true,这些节点无法通行;(3)CLOSED表中的节点,这些节点已被访问.将排除后的所有节点放入OPEN表,计算它们的g(j)值和f(j)值,并设置它们的父节点为起点PS.
3)从OPEN表中删除起点PS,并将其添加到CLOSED表.
4)从OPEN表中找出f(j)值最小的节点,将其从OPEN表中移出,并添加到CLOSED表,同时将该节点设置为当前节点S.
5)在ORIGINAL表中搜索所有与当前节点S相邻的节点,排除具有以下特征的节点:(1)θ1、θ2不满足条件;(2)isObstacle状态为true;(3)CLOSED表中的节点.将排除后的所有节点放入OPEN表,计算它们的g(j)和f(j)值:并设置它们的父节点为S.
6)遍历步骤5)中搜索到并符合条件的节点,若节点不在OPEN表中,则将它添加进OPEN表,计算它的g(j)和f(j),并设置它的父节点为S,若节点已经在OPEN表中,计算新的路径(即经过S到达该点的路径)的g(j)值:若g(j)值高于原值,说明这不是一个明智的选择,因为其耗费更高;若g(j)值低于原值,意味新的路径是更好的选择,首先将该节点的父节点更新为当前节点S,然后重新计算它的g(j)和f(j)值.在所有产生新路径的节点中,选择f(j)值最小的作为路径的节点,将其父节点S从OPEN表移至CLOSED表,并更新该节点为当前节点S.转到步骤5),直至OPEN表中出现终点PE,退出循环.
7)最后,从终点PE开始,沿每一节点的父节点回到起点PS,连接而成的路径就是所要求解的最优路径.
算法的代码及实现步骤如下:
public class BestPath{
oriList//初始列表
openList//开启列表
closedList//关闭列表
startNode//起始节点
endNode//目标节点
currentNode//当前节点
public BestPath(){
openList.Add(startNode)//将起始节点添加到开启列表
currentNode=startNode;
do{
currentNode=searchFminNode(currentNode)//寻找开启列表中F值最低的节点,并将其置为当前节点
closedNode.Add(currentNode) //将当前节点切换到关闭列表
currentNode=searchNode(currentNode)//搜索当前节点的相邻节点
}while(endNode∈openList)//直到目标节点出现在开启列表中,这时路径被找到
}
private Node search FminNode(Node goalNode){
for each node//遍历所有相邻的节点
if(node->{θ1&θ2}&&node.isObstacle==false&&node∉closedList)//如果节点满足条件
{
openList.Add(node)//将节点添加到开启列表
calc F(node)//计算节点的F值
node.preNode=goalNode//设置节点的父节点为goalNode
}
return FminNode//返回至F值最小的节点
}
private Node searchNodes(Node goalNode){
for each node//遍历所有相邻的节点
if(node!->{θ1&θ2}&&node.isObstacle==true&&node∈closedList) //如果节点不满足夹角条件或不可通过或已经在关闭列表中
{
//什么也不做
}
{
openList.Add(node)//将节点添加到开启列表
node.preNode=goalNode//设置节点的父节点为当前节点
calc GF()//计算该节点的G值和F值 }
if(node∈openList)//节点已经在开启列表中
{
node.NewG=calcNewG()//计算经过goalNode到该节点的新路径的G值
if(node.NewG<node.G)//若新值低于原值,因为新的路径是更好的选择
{
node.preNode=goalNode//设置节点的父节点为当前节点
closedNode.Add(goalNode)//将当前节点切换到关闭列表
reCalc GF()//重新计算该节点的G值和F值
}
}
return FminNode//返回F值最小的节点
}
}
3 实例与效率分析
为验证模型和算法的有效性,采用江苏省某地区220kV输电线路规划对模型和算法进行实例验证.在输电线路规划中,影响线路设计的主要因素有居民区、自然保护区、水源保护区、森林公园、风景名胜区等环境敏感区,以及空间距离、高程、坡度等地形影响因素[10].环境敏感区是禁止通行的区域,因此将其作为障碍因素,地形影响因素需计算其通行代价.根据已有栅格数据的分辨率以及线路规划精度要求,构建多分辨率栅格数据模型,模型中的空间距离、高程、坡度的影响权重分别设定为0.7,0.2,0.1.图4为构建的规划区域的变分辨率栅格数据模型.

图4 规划区域的变分辨率栅格数据模型Fig.4 Variable resolution raster data model of planning area
首先对模型的有效性进行验证.实验结果如图5所示,图5(a)、(b)为单分辨率栅格数据模型,其中(a)的分辨率较低,(b)的分辨率较高,(c)为本文提出的变分辨率栅格数据模型.图5(a)中的路径受到地物“边缘效应”的影响,为避开障碍物需绕道而行,(b)和(c)都成功避开了障碍物,并且得到了比(a)更短的最优路径,但(b)中单元格的数量远远大于(c),造成数据冗余度较高,同时也增加了路径寻优的计算成本,而(c)不仅正确地寻找最优路径,而且极大地降低了数据冗余度及计算成本.

图5 3种模型的线路规划结果Fig.5 Route planning results of three kinds of models
然后对算法的有效性进行验证.在变分辨率栅格数据模型中选取Dijkstra、A*和本文提出的启发式有向搜索算法求解最优路径(见图5(c)),结果如表1所示.从表1的实验结果可知,Dijkstra算法由于在搜索节点时的盲目性,需要搜索的空间庞大,找到最优路径的时间较长,而A*算法由于增加了启发式信息,大大减少了搜索节点数,找到最优路径所需的时间远短于Dijkstra算法.而本文提出的启发式有向搜索算法对A*算法做了改进,引入了有向搜索方法,使得搜索的节点数减少了近一半,从而提高了寻找最优路径的时间效率.

表1 3种算法比较Table 1 Comparison of three algorithms
4 结 语
提出了变分辨率栅格数据模型,该模型克服了传统单分辨率栅格数据模型在进行最优路径分析时无法兼顾地形表达精度和数据冗余度的弊端,避免了地物“边缘效应”的影响.同时,在模型的基础上,对A*算法进行了改进,通过引入启发式有向搜索方法,减少了搜索空间,提高了算法的计算效率.本文虽然考虑了坡度等地形因素,但最后得到的最优路径的空间距离为水平距离,如何计算实际距离有待进一步研究.总之,该方法能有效解决连续空间中最优路径的求解问题,可应用于道路工程设计、输电线路选址等领域.
参考文献(References):
[1] 张万绪,张向兰,李莹.基于改进粒子群算法的智能机器人路径规划[J].计算机应用,2014(2):510-513.ZHANG Wanxu,ZHANG Xianglan,LI Ying.Path planning for intelligent robots based on improved particle swarm optimization algorithm[J].Journal of Computer Applications,2014(2):510-513.
[2] 赵开新,魏勇,王东署.改进蚁群算法在移动机器人路径规划中的研究[J].计算机测量与控制,2014(11):3725-3727.ZHAO Kaixin,WEI Yong,WANG Dongshu.Research of improved ant colony algorithm in mobile robot path planning[J].Computer Measurement &Control,2014(11):3725-3727.
[3] 简毅,张月.移动机器人全局覆盖路径规划算法研究进展与展望[J].计算机应用,2014(10):2844-2849,2864.JIAN Yi,ZHANG Yue.Complete coverage path planning algorithm for mobile robot:Progress and prospect [J].Journal of Computer Applications,2014(10):2844-2849,2864.
[4] 康冰,王曦辉,刘富.基于改进蚁群算法的搜索机器人路径规划[J].吉林大学学报:工学版,2014(4):1062-1068.KANG Bing,WANG Xihui,LIU Fu.Path planning of searching robot based on improved ant colony algorithm[J].Journal of Jilin University:Engineering and Technology Edition,2014(4):1062-1068.
[5] 孙永,刘靖旭,宋留勇.复杂地理环境下基于障碍距离的最短路径寻优算法[J].测绘科学,2014(2):37-41,68.SUN Yong,LIU Jingxu,SONG Liuyong.Study of shortest paths optimization algorithm based on obstructed distance under complexity geographical environment[J].Science of Surveying and Mapping,2014 (2):37-41,68.
[6] 厍向阳,史经俭,罗晓霞.栅格数据模型中附有条件的最短路径算法[J].计算机应用,2008(4):856-859.SHE Xiangyang,SHI Jingjian,LUO Xiaoxia.Shortest path algorithm confined to conditions in grid data model[J].Journal of Computer Applications,2008(4):856-859.
[7] CHOI Yosoon,UM Jeonggi,PARK Myongho.Finding least-cost paths across a continuous raster surface with discrete vector networks[J].Cartography and Geographic Information Science,2014,41(1):75-85.
[8] 鲁敏,张金芳.栅格地形的最优路径分析[J].武汉大学学报:信息科学版,2010(1):59-63.LU Min,ZHANG Jinfang.Least-cost path analysis in raster terrains[J].Geomatics and Information Science of Wuhan University,2010(1):59-63.
[9] 严瑞,龙毅,郑玥,等.顾及地形起伏的步行最优路径分析算法[J].武汉大学学报:信息科学版,2012(5):564-568,572.YAN Rui,LONG Yi,ZHENG Yue,et al.An optimal walking path algorithm considering terrain influence [J].Geomatics and Information Science of Wuhan University,2012(5):564-568,572.
[10] 舒隽,韩冰,陈学姣.计及线路路径优化的空间电网规划[J].中国电机工程学报,2014(4):570-577.SHU Jun,HAN Bing,CHEN Xuejiao.Spatial power network planning considering electric line route optimization[J].Proceedings of the CSEE,2014(4):570-577.
Heuristic directional search optimal path algorithm based on the variable raster model
HUA Jianfeng1,2,ZHANG Feng1,2,DU Zhenhong1,2,LIU Renyi1,2,LI Rongya1,2(1.Zhejiang Provincial Key Lab of GIS,Zhejiang University,Hangzhou310028,China;2.Department of Geographic Information Science,Zhejiang University,Hangzhou310027,China)
Journal of Zhejiang University(Science Edition),2016,43(1):051-056
Abstract:For graph theory method cannot be directly used to approach the path analysis problems in continuous space,a variable resolution grid model based on quad-tree thought is figured out.This model not only takes into account the topographic expression accuracy and data redundancy,but also avoids the impact of the“edge effect”.On the basis of the model,a heuristic directional search algorithm is designed,in which a directional search method is introduced.The algorithm firstly selects nodes according to the direction when searching for adjacent node,thereby reducing the search space and improving the efficiency of the algorithm.Experimental results show that the model and the algorithm proposed can not only obtain the optimal path in continuous space,but also have high computational efficiency.
Key Words:optimal path;continuous space;variable resolution;raster model;directional search method
通信作者*,E-mail:duzhenhong@zju.edu.cn.
作者简介:华剑锋(1989-),男,硕士研究生,主要从事GIS开发及其在水利、公共卫生等领域的应用研究.
基金项目:国家自然科学基金资助项目(41471313,41101356);浙江省科技攻关计划项目(2013C33051);国家海洋公益性行业科研专项经费资助项目(2015418003,201305012);国家科技基础性工作专项(2012FY112300);中央高校基础科研业务费专项(2013QNA3023).
收稿日期:2015-05-05.
DOI:10.3785/j.issn.1008-9497.2016.01.009
中图分类号:P208
文献标志码:A
文章编号:1008-9497(2016)01-051-06

