合龙方案对多跨连续梁桥施工监控的影响分析

包仪军，丁明波，朱　龙

(兰州交通大学土木工程学院，兰州　730070)



合龙方案对多跨连续梁桥施工监控的影响分析

包仪军，丁明波，朱龙

(兰州交通大学土木工程学院，兰州730070)

摘要:多跨连续梁的合龙顺序对结构成桥累计位移和内力有较大影响，以1座(48+4×80+48) m预应力混凝土连续梁桥为例，根据不同的合龙方案确定3种工况，对不同工况下的桥梁结构建立不同结构体系转换的施工阶段分析有限元模型，分析合龙顺序及合龙期间的预应力张拉阶段对施工阶段的预拱度及成桥内力的影响，对比分析多跨连续梁桥合龙口两端产生较大位移差的原因。提出多跨连续梁桥线形监控难度的主要影响因素为累计位移最大值和合龙口两端的累计位移差。结果表明，合龙顺序对梁体施工中的预拱度设置量影响较大，特别是不同结构体系下预应力张拉效应差别较大，合理的合龙顺序和分批分阶段张拉预应力可降低施工过程中线形监控的难度，根据分析结果提出合理的合龙顺序建议。

关键词:多跨连续梁;合龙顺序;线形监控;体系转换;预拱度

悬臂施工的多跨连续梁结构的成桥累计位移及最终成桥内力在很大程度上受合龙顺序、临时支座拆除顺序、预应力张拉阶段的影响［1，2］，虽然混凝土的徐变作用使最终成桥内力向一次性落架的内力趋势发展，但其最终成桥内力和施工过程中的累计变形还是存在较大的差异。

目前对于多跨连续梁桥在结构设计、施工监控方面的研究较多，而对多跨悬臂施工的合龙顺序对结构成桥内力和累计变形的影响的研究较少。在多跨连续梁桥的设计方面，对其最终成桥内力及运营阶段的安全性考虑较多，而对成桥累计变形及施工过程中梁体线形是否容易控制的考虑较少。张谢东［3］从合龙时间、合龙方案的选择、合龙顺序、体系转换以及施工配重等方面对预应力混凝土连续梁的合龙段施工做了研究并成功应用于实际的桥梁施工控制。王兵见［4］分析了一次落架合龙和逐段现浇合龙两种方案对主梁累计位移和受力的影响。石现峰［5］以1座三跨混凝土连续梁桥为例分析比较了采用3种施工方法(一次落架法、逐跨施工法及悬臂施工法)对成桥后由于自重引起的结构内力及变形的影响，同时还比较分析了两种常用的徐变模式对桥梁结构的长期影响。易锦［6］以1座12跨刚构—连续组合梁桥为工程背景，对5种合龙方案和3种体系转换顺序进行数值模拟，探讨合龙次序和体系转换顺序对该类桥梁的受力和变形规律。以6跨连续梁为工程背景，分析了线形监控难度的决定性因素，设计了不同的合龙顺序并进行了分析，对比分析了多跨连续梁桥合龙口两端产生较大位移差的原因，并分析了不同合龙顺序对最终成桥内力的影响。

1　工程背景及设计合龙工况

新建合福铁路武步溪特大桥(48+4×80+48) m预应力混凝土双线连续梁桥，桥梁总体布置如图1所示。边支座中心线至梁端0.75 m，梁全长417.5 m，梁体为单箱单室，变截面、变高度结构，梁高沿纵向按二次抛物线变化，合龙段长度2 m。

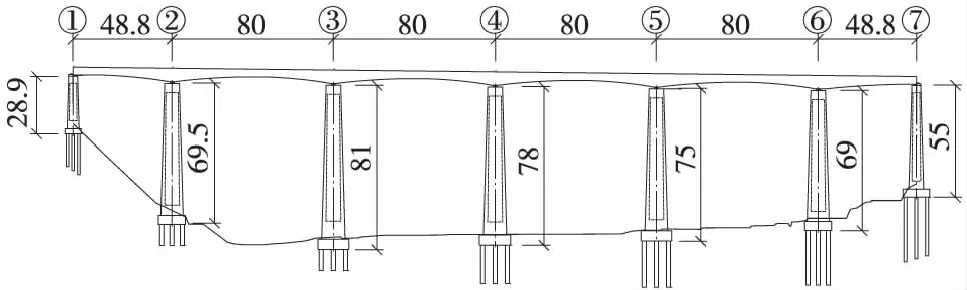
图1　桥梁总体布置(单位:m)

本桥采用悬臂浇筑施工工艺，桥梁上部结构设计施工方案为:墩梁固结→悬臂阶段施工→次边跨合龙→张拉次边跨钢束→边跨合龙→张拉边跨钢束→浇筑中跨合龙段→张拉中跨部分钢束→解除临时固结、张拉中跨剩余钢束→成桥→加载二期恒载。

为找出最优合龙方案以及不同合龙方案对主桥成桥后位移的影响规律，确定以下3种合龙工况进行对比分析，各合龙工况计算模型的荷载、边界条件、材料参数和预应力张拉顺序均不变。临时固结的拆除时间均为合龙口合龙后，张拉部分预应力束后拆除合龙口两相邻桥墩的临时固结，合龙段预应力均为一次全部张拉，具体合龙工况见表1。

表1　合龙过程施工工况

工况1的合龙顺序及体系转换过程见图2。全桥从墩顶0号块开始悬臂对称施工的受力状态与静定的T形刚构状态相似，如图2(a)所示;图2(b)为次边跨合龙体系转换后，结构转换为简支带双悬臂的结构体系;图2(c)为边跨合龙体系转换后，结构转换为2跨连续梁带单悬臂的结构体系;最后中跨合龙完成全部体系转换形成6跨连续梁，如图2(d)所示。悬臂施工中的合龙是一个对称施工的过程，可使结构稳定，受力对称［7］。

合龙段施工是多跨连续梁施工和体系转换的一个重要环节，需要通过有限元模型详细计算分析不同合龙顺序下各个施工阶段的位移和应力。采用有限元软件进行施工阶段模拟分析，按照实际的悬臂施工工序，模拟梁段节段的形成、荷载的加载、边界条件的转化以及结构体系转变等因素对结构挠度变形的影响。全桥共划分为182个单元，183个结点，结构离散模型如图3所示。

图2　工况1合龙顺序

图3　全桥离散模型

2　合龙顺序对线形控制难度的影响

为使悬臂施工连续梁桥的成桥线形满足设计及运营要求，在施工过程中需要进行线形控制，设置合适的预拱度值，这就要求在确定立模高程时全面考虑所有因素的影响，连续梁的预拱度与其形成过程和合龙顺序有着直接的联系，同一座连续梁若合龙顺序不同，其预拱度也有很大的不同［8］。

立模高程的计算公式如下

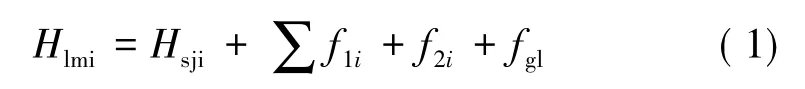
式中Hlmi——第i梁段前端立模高程;

Hsji——第i梁段前端设计高程;

∑f1i——第i梁段前端从安装到成桥收缩徐变完成的累计位移值，含自重、预应力、混凝土收缩徐变、二期恒载等所有因素对此端前端位移的影响; f2i——使用荷载在i梁段引起的挠度的50%; fgl——挂篮前端变形值。

施工监控难度的相关影响因素分析如下。

(1)累计位移最大值。若累计位移较大，需设置较大的预拱度，预拱度设置偏大或者偏小都会影响桥梁结构的整体线形，对于无砟轨道桥梁，会影响桥面的平顺性和轨道板的铺设。

(2)合龙口两端的累计位移差。合龙段长度一般为2 m，若两端累计位移差过大，合龙口两端的预拱度会有较大的差值，若实际发生的位移与预估位移有一定的误差，则会影响局部线形和总体线形。在多跨连续梁悬臂施工中，后续施工产生的荷载会对先施工的梁段产生弹性变形，而已施工的节段在自重、预应力等荷载作用下已完成了弹性变形，不会对后施工的节段产生弹性变形。多跨连续梁先边跨合龙时，由于两端结构形式的不同，一端为T构悬臂端，一端为边跨现浇段，合龙段两端产生的累计位移值也不同，如图4 (a)所示，在边跨合龙及体系转换的过程中，在拆除临时支座时，在边跨预应力的作用下，支座位置梁体会产生转角，悬臂端会产生直线的下降或上升的形变，一般，若边跨预应力张拉较多，次边跨悬臂端会下降，边跨上升，如图4(b)所示，此部分位移大都在拆除临时支座后瞬间发生，若预测不当出现误差，较难调整，对后续中跨的合龙影响很大。对于先中跨合龙后边跨合龙的桥梁，中跨合龙并拆除临时支座的过程中，边跨悬臂段亦会产生向上或向下的形变，从而在边跨合龙口形成累计位移差，影响边跨的合龙及梁体的线形。多跨连续梁合龙顺序的不同，合龙段的累计位移差亦不同。合龙段两侧的累计差值越大，施工控制难度越大，易产生较大的合龙误差，通过改变合龙顺序可使合龙段位移差达到最优，从而降低施工控制的难度，保证成桥后梁体线形更好。

通过有限元分析，模拟不同合龙工况下的施工过程，各施工工况下合龙段成桥累计位移及位移差见表2，由恒载累计位移及活载产生的各工况预拱度比较(仅示出一半)如图5所示。

图4　多跨连续梁变形特点

表2　各工况合龙口两侧成桥累计位移及位移差cm

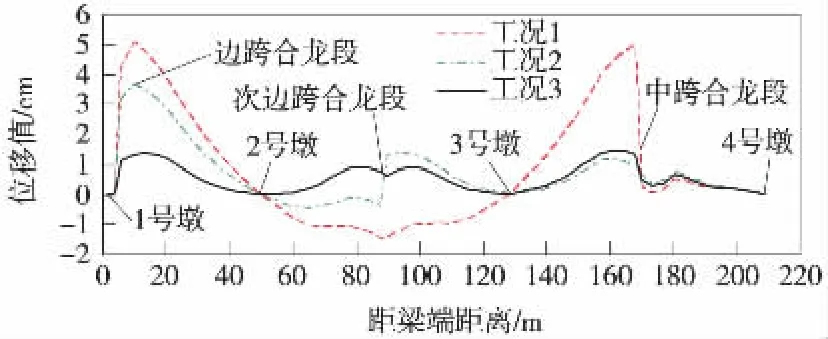
图5　预拱度比较

根据竖向累计位移及预拱度的比较，得出以下结论。

(1)工况1下各个合龙段的累计位移明显大于工况2、工况3，因此工况1在桥梁线形控制时所提供的预抛高较大，体系转换过程中位移变化过大，容易产生不可控因素，增加施工控制的难度。通过分析发现，工况1在次边跨合龙后在预应力的作用下，外悬臂端产生了向下3 cm的位移，次边跨合龙段产生了向上1.9 cm的位移，故工况1产生如此大累计位移差的主要原因是简支带外悬臂结构体系受预应力作用后，支点位置发生了较大的转角，从而引起悬臂端较大累计位移。

通常，预应力作用下会产生两种效应，预应力的直接效应和本阶段的徐变变形，为了分析次边跨合龙后预应力张拉的徐变效应，基于Torst-Bazant方法，作者［9］采用积分中值定理推倒出了计算徐变变形增量的代数方程(公式(2) )。采用该方程对次边跨合龙后的预应力徐变变形效应进行计算，绘制了考虑徐变和不考虑徐变下预应力张拉产生的位移，如图6所示。

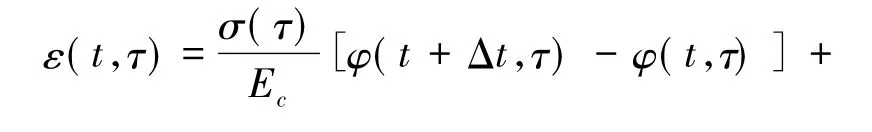
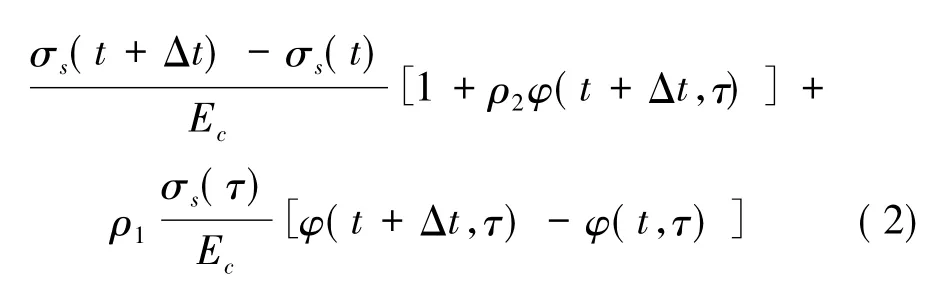
式中，σ(τ)为初始时刻τ时混凝土的应力; Ec为龄期τ时的混凝土弹性模量;σs(t)为时刻τ至t产生的应力增量;φ(t，τ)为徐变系数;ρ1，ρ2为系数。

徐变系数的计算一般采用线性徐变理论(工作应力满足)，文献［10］采用了CEB－FIP(1900)模型，该模型对徐变系数的预测采用了乘积的表达式。该模型考虑了混凝土特征抗压强度、构件尺寸、环境相对湿度、持荷时间、加载龄期和水泥种类等参数的影响。计算公式如下

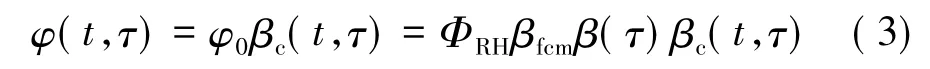
式中，φ0为名义徐变系数;ΦRH为环境相对湿度修正系数;βfcm为混凝土强度修正系数;β(τ)为加载龄期修正系数;βc(t，τ)为徐变进程时间系数。

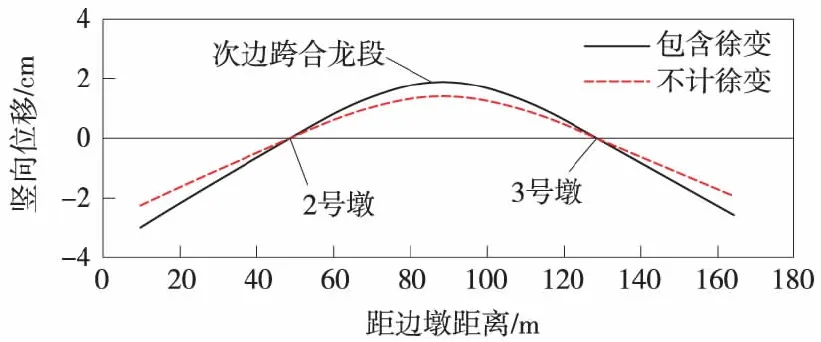
图6　次边跨合龙张拉钢束竖向位移

从图6可以看出，在次中跨合龙后预应力张拉过程中徐变效应显著，在两个悬臂端徐变变形达到了0.63 cm，占总位移的24.6%，在次中跨合龙位置达到了0.49 cm，占总位移的25.8%。因此通过选择合适的预应力张拉工序，减小徐变效应，也可以达到降低合龙段累计位移差的目的。

为此，针对工况1的合龙顺序在合龙后在保证结构施工过程安全的情况下不张拉全部的合龙段预应力(次中跨合龙张拉CB6～CB9、CT16、CT17，边跨合龙张拉SB4～SB7、ST14、ST15，中跨合龙后张拉中跨的全部预应力及次边跨的CB1～CB5、CW1～CW3及边跨的SB1～SB3、SW1、SW2)，定义为工况4。对工况1及工况4的预拱度进行比较，如图7所示。

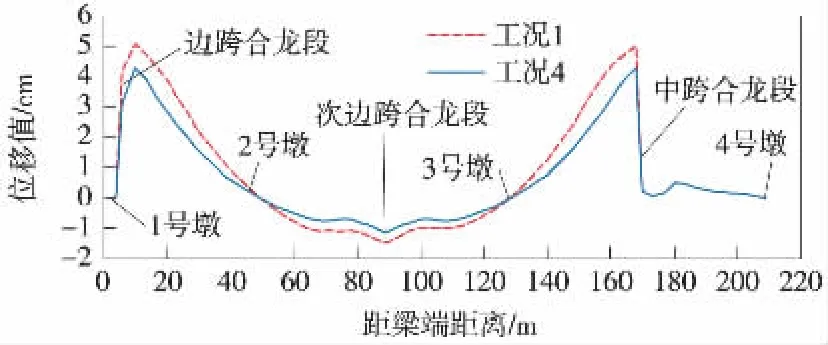
图7　工况1及工况4预拱度比较

由图7可以看出，对合龙段预应力的张拉阶段进行调整，可以有效降低预拱度的最值及合龙段差值，这是因为成桥后的结构体系总体刚度较大，由预应力引起的位移量较小。表3列出了工况1及工况4的合龙段累计位移差，由此可知通过调整预应力张拉阶段减小的累计位移差值达到了1.71 cm，达到了总位移差值的35.9%。

表3　合龙段两侧累计位移差　cm

(2)由表2分析知，工况1下各合龙段累计位移远大于工况3，合龙段位移差为相邻合龙口合龙张拉后拆除临时固结的瞬间产生，若产生合龙误差，较难调整，若强制调整将导致梁体应力集中和次内力过大。

(3)合龙顺序的差异直接影响桥梁的预拱度。由预拱度最值及预拱度变化趋势可以看出在工况1下，全桥的预拱度较大，而且有较大的跳跃性。分析其原因，主要是因为合龙前两侧结构体系不同，累计位移也有较大差异。相比之下，工况3的预拱度最小，且在每个合龙段处的连续性较好，便于施工时立模高程的设置，减小控制难度，使成桥后的线形更接近于设计线形。

3　合龙顺序对成桥应力的影响

连续梁桥的最终恒载内力与施工合龙的程序有密切关系，不同的施工程序，其初始恒载内力不同，在体系转换过程中，引起的内力重分布的数值随之不同［11］。合龙段两侧的合龙误差对多跨连续梁成桥后的应力也有明显影响，合龙误差越大，越容易引起预应力孔道在合龙位置形成折角，则预应力钢束对下缘的混凝土会产生集中力，造成混凝土的开裂或崩裂［12］。同时，合龙误差越大，则合龙时结构将产生很大的次内力，不利于梁体受力。表4列出了各工况下的应力值及应力差值，各截面上下缘应力如图8所示，图中仅示出全桥的一半。

通过对各个工况应力的比较可知:

(1) 3种工况下各截面的应力变化趋势是一致的，均向一次性成桥内力发展;

(2)工况1上缘应力较工况2、工况3大，最大应力差达到了2.69 MPa;各墩墩顶处工况1的下缘应力略小于工况2、3，应力差值在1.0 MPa左右;工况1的下缘应力与工况2、3相比较，越靠近合龙段越大。

分析工况1应力较工况2、工况3产生如此大差值的原因，简支带外悬臂体系在预应力张拉过程中产生的应力大。为了分析各个工况下张拉次边跨预应力时产生的应力，作了如图9所示的预应力效应应力图。

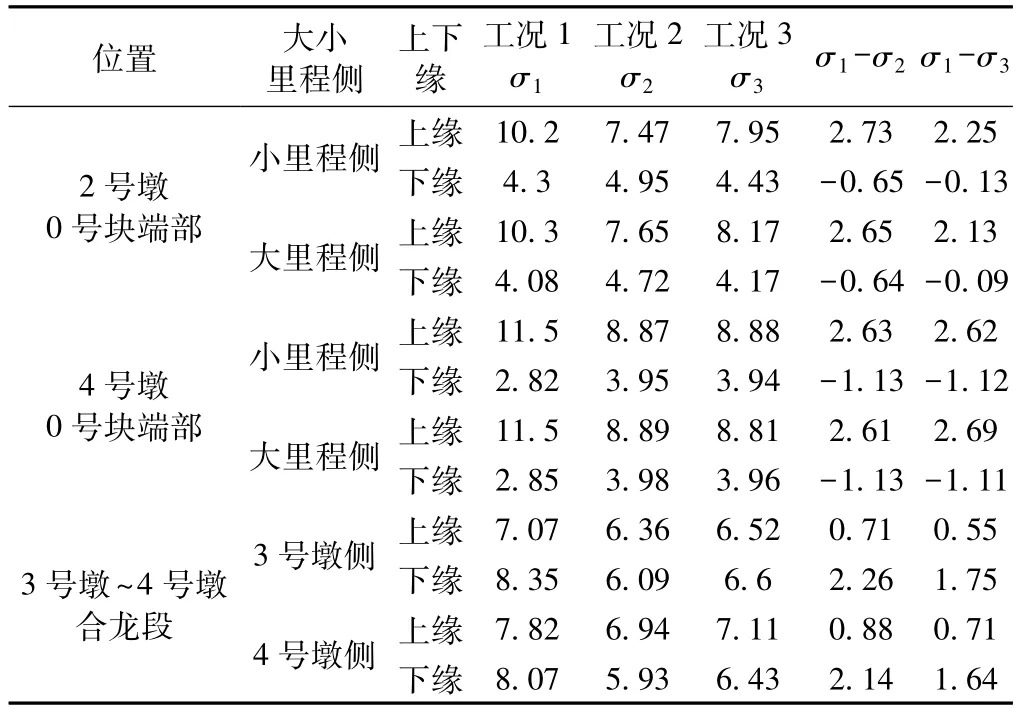
表4　各工况关键位置应力值比较　MPa

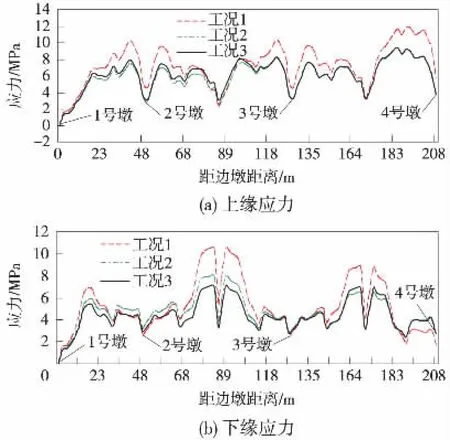
图8　各工况上、下缘应力

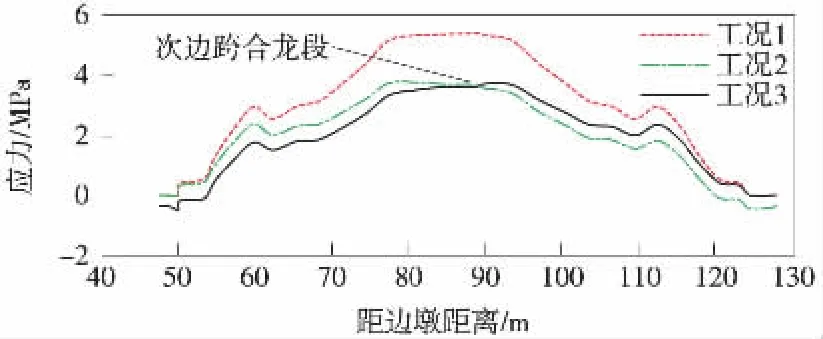
图9　张拉次边跨预应力

通过对图9分析发现，张拉次边跨预应力时，工况1较工况2、工况3产生较大的应力，在次边跨合龙段位置达到了5.37 MPa，与工况2的应力差值达到了1.82 MPa。因此简支带外悬臂体系在张拉预应力时对梁体应力影响大，可通过调整预应力张拉工序来优化梁体应力分布。

(3)合龙顺序的不同对多跨连续梁成桥应力有一定的影响。对各个工况成桥应力对比分析，发现各工况下应力都满足运营要求。为了使成桥后梁体受力更合理，应针对不同的合龙顺序下设计不同的预应力钢束布置。

4　结语

本文对多跨连续梁合龙顺序进行了有限元分析，对比分析了各合龙工况下的累计位移、合龙口位移差、梁体应力等，对多跨连续梁合龙顺序的设计有一定的参考意义。

(1)多跨连续梁悬臂施工结构体系转换复杂，为了成桥后达到理想线形，必须对其进行施工监控，多跨连续梁桥的合龙顺序为影响其预拱度设置的主要因素，因此，在多跨连续梁合龙顺序的选择上应引起重视。

(2)先次边跨、再边跨、最后进行中跨的合龙顺序预拱度较大，且由于合龙段两侧的累计位移差较大，线形监控的难度较大，合龙段位移差为最大悬臂施工完成后产生，若产生误差，较难调整。若在施工现场条件允许的情况下，不建议采用。

(3)合龙口两端累计位移差主要由合龙过程中张拉的预应力产生，简支带外悬臂的结构体系，在张拉预应力时对整个结构的变形及内力均有较其他结构体系显著的影响，其主要原因是此体系竖向刚度小并有较大的徐变效应，可通过分阶段张拉预应力来调整减小其影响。

(4)先边跨、再次边跨、最后中跨的合龙顺序，从理论分析上来讲是最优的，其预拱度最小且连续性好，应力也相对较小，在受力上更符合要求。

参考文献:

［1］陈秀清，裴万胜，程菊红，等.预应力混凝土连续梁桥合龙顺序对成桥状态的影响研究［J］.铁道建筑，2013(12):19-21.

［2］朱雷，熊锐，颜岩.悬臂施工连续梁桥合龙线形应力分析［J］.交通科技，2013(1):10-12.

［3］张谢东，詹昊，舒洪波，等.大跨度预应力混凝土连续梁桥合龙施工技术研究［J］.桥梁建设，2005(2):63-66.

［4］王兵见，陈云海.体系转换对多跨连续梁悬臂施工控制的影响分析［J］.公路交通科技，2009(10):132-133，170.

［5］石现峰，李建中.施工方法对混凝土连续梁桥内力及变形的影响［J］.工程力学，1998(2):543-549.

［6］易锦，贺国京，陆杰，等.合龙及体系转换顺序对多跨刚构－连续组合梁桥影响分析［J］.铁道科学与工程学报，2013，10(5):23-27.

［7］王学华.合龙顺序对高速铁路连续梁桥的影响分析［J］.铁道标准设计，2014，58(7):72-75.

［8］杨帆.宜万铁路叶溪河大桥(70+108+70) m连续梁桥合龙方案优化设计［J］.铁道标准设计，2012(7):55-59.

［9］范立础.桥梁结构徐变次内力分析［J］.同济大学学报:自然科学版，1991，19(1):23-32.

［10］中华人民共和国交通部.JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京:人民交通出版社，2004.

［11］范立础.预应力混凝土连续梁桥［M］.北京:人民交通出版社，1985.

［12］冯鹏程，吴游宇，杨耀铨，李朝阳.连续刚构桥底板崩裂事故的评析［J］.世界桥梁，2006(1):66-69.

Research on the Effect of Closure Program on Construction Monitoring of Multi-span Continuous Beam Bridge

BAO Yi-jun，DING Ming-bo，ZHU Long
(School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)

Abstract:The closure order of multi-span continuous beam often exerts eminent influence on the cumulative displacement and internal force of the bridge structure.With reference to a pre-stressed concrete continuous beam bridge of (48+4×80+48) m，finite element models are established with respect to three different conditions according for each different closure program to analyze the effects of closure order and pre-stress tensioning in the process of closure on the camber and the internal force during the construction and the causes of displacement difference between the closure ports.It is concluded that the main influencing factors impacting the monitoring are the maximum accumulated displacement and the accumulated displacement difference between closure ports.The results indicate that the setting of camber is greatly influenced by the closure order，especially，the difference in pre-stressed tensioning effect for different structural systems is very big.As reasonable closure order with phased pre-stressed tensioning may facilitate the linear control in construction process，reasonable closure order is proposed based on analysis results.

Key words:Multi-span continuous beam; Closure order; Linear monitoring; System transformation; Camber

作者简介:包仪军(1990—)，男，硕士研究生，E-mail:1203916904 @ qq.com。

收稿日期:2015-08-17;修回日期:2015-08-26

文章编号:1004-2954(2016) 03-0082-05

中图分类号:U448.21

文献标识码:A

DOI:10.13238/j.issn.1004－2954.2016.03.018