水轮发电机组调速系统的非线性输出响应分析

夏　鑫，倪　伟，周建中

(1.淮阴工学院自动化学院，江苏淮安223003；

2.华中科技大学水电与数字化工程学院，湖北武汉430074)



水轮发电机组调速系统的非线性输出响应分析

夏鑫1，倪伟1，周建中2

(1.淮阴工学院自动化学院，江苏淮安223003；

2.华中科技大学水电与数字化工程学院，湖北武汉430074)

摘要：针对水电机组调速系统结构复杂且存在诸多非线性环节，提出了一种基于非线性输出频率响应函数的水轮发电机组调速系统分析方法，该方法可以很好的避免调速系统建模困难的问题，同时又能较好地反应调速系统模型的非线性特性。首先，建立了具有非线性特性的调速系统模型。进而对不同工况参数下的调速系统进行仿真，利用仿真数据辨识出各工况下的NOFRFs模型。最后，对调速系统各工况下的NOFRFs进行分析。实验仿真结果指出，所提方法能够清晰的描述运行工况变化时调速系统的非线性变化特性，为调速系统的优化控制与故障诊断提供了一定的理论依据。

关键词：调速系统；非线性输出响应；参数辨识；水轮发电机组

0引言

随着大规模互联电网的发展，电力系统安全稳定运行已成为当前研究的热点。水轮发电机组在电力系统中承担着功率调节与频率调节的作用，而其调速系统直接影响了其调节品质，进而影响到电网中电能的质量。国内外许多学者[1- 8，10]对调速系统的参数辨识与优化及控制策略进行了广泛的研究。大多数学者[2- 5]在研究调速系统模型时采用刚性水击水轮机线性模型，而水轮发电机组是一个由水力、机械、电力等因素耦合的复杂非线性系统，线性调速系统模型不能全面反映水电机组的运行特性。目前对非线性调速系统的研究也取得了一些进展[1，6- 10]，但大多数研究只是针对调节参数的优化而开展，并未对调速系统的非线性本质进行深入分析。因而开展水电机组调速系统非线性响应研究对调速系统的优化控制与故障诊断有积极的支持与指导作用。

水轮发电机组调速系统中存在水锤效应、水门开度限幅、机械响应死区等非线性因素，其精细化的数学模型难以建立。Volterra级数模型作为一种有效的非线性建模方法，近年来，受到了学者的广泛的关注和应用[11，12]。Volterra模型的频域形式广义频率响应(generalized frequency response function，GFRF)是一种有效的非线性系统频域分析方法。由于广义频率响应函数存在维数灾的问题且其表达不直观，因而在实际应用中受到了很大的限制。Lang[13]提出了一种非线性输出频率响应函数(nonlinear output frequency response functions，NOFRFs)，它是GFRF的一维变化形式，对于分析非线性系统的响应特性具有重要的理论价值。

本文在建立了非线性水轮机组调速系统模型的基础上，辨识得到非线性调速系统的频率输出响应函数，通过对不同参数下的调速系统非线性响应分析，从本质上揭示了调速系统的非线性特征，为调速系统的优化控制与故障诊断提供了一定的理论依据。

1非线性调速系统模型

1.1PID控制器与电液伺服系统

目前，具有PID控制规律的控制器在水轮机调速系统中广泛应用。本文采用的PID控制器与电液伺服系统的结构如图1所示。对电液随动系统考虑了死区、接力器限幅等非线性环节。

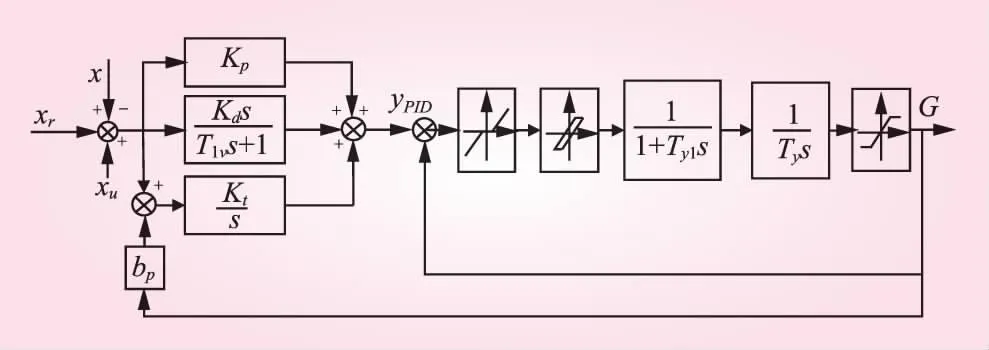
图1　PID控制器与电液伺服系统

图中，xr为给定频率；x为机组频率；xu为扰动频率；kp、kd、ki分别为比例、微分和积分系数；T1v为微分滤波时间常数；bp为永态差值系数；Ty1为主配压阀反应时间常数；Ty为主接力器反应时间常数；G为导叶开度。

1.2刚性水击非线性水轮发电机组模型

当前对水轮机非线性模型的研究主要可分为3类：基于水轮机全特性曲线插值的非线性水轮机模型；基于水轮机过渡过程的内特性模型；IEEE提出的水轮机简化非线性解析模型[8，9]。由于全特性曲线一般难以获取，而基于过渡过程的内特性模型结构对工况参数要求极其严格，因而本文选取了模型相对简单但工程应用价值较大的水轮机简化非线性解析模型。其将水轮机近似为阀门处理，考虑了压力引水管道的作用，模型方程可表示为

(1)

式中，Pm为机械功率相对值；At为比例系数；q、Qnl为水轮机流量和空载流量相对值；D为速度偏差阻尼系数；G为导叶开度相对值；Tw为管道水击时间常数；fp为水头损失系数；h为水头相对值。

对于同步发电机仅考虑转子转速动态特性，忽略转子摩擦等因素，同步发电机模型可以简化为一阶模型，其传递函数表示为

(2)

式中，x为机组频率；Ta为机组惯性时间常数；eg为自调节系数。

综上所述，刚性水击非线性水轮发电机组模型的结构可由图2表示。

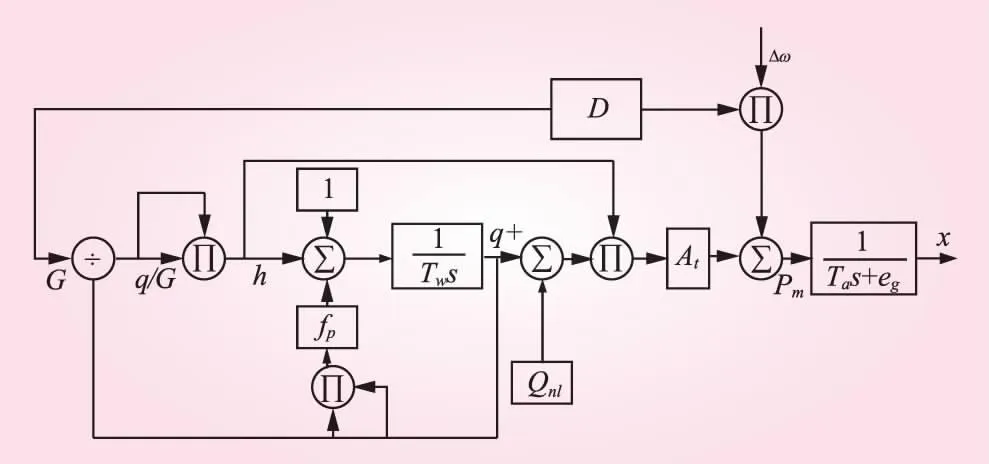
图2　刚性水击非线性水轮机组模型

2非线性输出频率响应分析方法

2.1刚性水击非线性水轮发电机组模型

水轮发电机调速系统中包含许多非线性环节，在控制动态过程中其数学解析模型表述异常复杂，不利于其非线性行为的分析。Volterra级数模型是非线性系统建模的最有效方法之一，其只关注系统的输入输出关系而不具体描述系统内部结构，非线性模型的输入输出关系可由Volterra级数模型表述如下

(3)

式中，u(t)为输入量，y(t)为输出量，hn(τ1，…，τn)为n阶时域核。

对式(3)进行多维傅里叶变换得到Volterra级数的频域模型

(4)

式中，Hn(jω，…，jω)称为广义频率响应；U(jω)、Y(jω)分别为输入u(t)、y(t)的傅里叶变化形式。由于广义频率响应存在维数高，计算困难且直观性差的问题，Lang[13]等提出了非线性输出响应模型将GFRF函数由多维变为一维，大大提高了非线性频率响应的应用价值。NOFRFs模型可表述为

(5)

由式(4)、(5)可得

(6)

2.2非线性输出频率响应函数辨识方法

将式(6)展开

(7)

将式(7)转换成矩阵形式

(8)

由式(8)可知，非线性输出响应函数与输入信号的频率有关与幅值无关，因而在辨识非线性输出响应函数时可以通过改变输入信号的幅值来达到激励系统的作用。若系统为N阶非线性模型，则对系统施加N次频率相同幅值不同的激励信号如式(9)所示

(9)

在N次激励下，式(8)可写成如下状态矩阵组

Y =Yr1Yi1︙YrNYiNéëêêêêêêêùûúúúúúúú=AUG

(10)

对式(10)进行最小二乘计算可得非线性输出频率响应函数

(11)

3仿真实验分析

本文按照前述水电机组调速模型进行仿真分析。具体参数参照某水电厂的实际运行设置如下：kp=2.65；kd=1；ki=1.25；bp=0.02；Ty1=0.02 s；Tw=0.5 s；T1v=0.01；At=1.06；Ta=5.7 s；eg=0；D=0。仿真时间设为500 s，仿真步长0.01 s。

3.1水轮机空载流量的响应

水轮机在运行过程中，由于导水机构漏水、轴承润滑不良等因素而导致水轮机空载流量发生变化，为分析由空载流量变化导致的水电机组调速系统非线性响应，做如下仿真分析。

图3　不同空载流量下的调速系统频率响应

设Ty=0.1 s，分析Qnl=0.1，Qnl=0.2和Qnl=0.3时的调速系统响应，在t=90 s时加入扰动信号xr(t)=0.05sin(t)，3种空载流量下的调速系统频率控制响应如图3所示。

从图3中可知，3种空载流量下其非线性响应差别不大，很难分析出空载流量对调速系统影响。为此，对调速系统输出响应做频谱分析如图4所示。

从图4中可知，调速系统的输出响应频谱同样难以描述调速系统中空载流量变化引起的非线性特征。

图4　空载流量为0.1，0.2，0.3时调速系统输出频谱

为此，采用本文所提出的非线性输出响应模型分析方法。因四阶以上频率成分影响较小，故本文采用前3阶频率对调速系统进行分析，设激励信号为xu(t)=0.05sin(t)，xu(t)=0.1sin(t)，xu(t)=0.15sin(t)，扰动信号的基频ωf=1/2π，表1为不同空载流量下调速系统的NOFRFs的主要倍频所对应值。

表1不同空载流量下NOFRFs值

阶数不同空载流量Qnl下的NOFRFs值Qnl=0.1Qnl=0.2Qnl=0.3G1(0.5jωf)0.13030.13430.1585G2(0.5jωf)2.96953.92335.1336G3(0.5jωf)0.95241.36191.3141G1(jωf)0.08140.08440.0639G2(jωf)60.349248.320736.7324G3(jωf)0.67440.07440.3718

从表1可以看出，随着空载流量的不断增大，在0.5倍频的G2值不断增加，而基频的G2值不断减小，说明G2值对空载流量的变化较为敏感。同时也指出空载流量的变化主要影响了调速系统的二阶非线性特性，通过对调速系统的二阶非线性特性的分析可以反推水轮机空载流量变化的趋势，为调速系统的优化控制与诊断提供一定的依据。

3.2主接力器响应时间常数的响应

调速系统主接力器的响应时间常数会因为润滑、油压等因素而发生变化，本文依据前面所提出的模型，设空载流量Qnl=0.2，对主接力器响应时间常数分别为Ty=0.1，Ty=0.15和Ty=0.2时进行了非线性输出响应分析，仿真设置与之前相同，NOFRFs的主要倍频所对应值如表2所示。

从表2中可以看出，随着主接力器时间常数的增加，其主要非线性变化集中在以0.5倍频为主的各阶NOFRFs，而基频的NOFRFs变化不大。结果指出，主接力器时间常数的变化对0.5倍频的各阶NOFRFs影响较大，可作为主接力器时间常数变化分析的依据。

表2不同主接力器响应时间常数下NOFRFs值

阶数不同主接力器响应时间常数Ty下的NOFRFs值Ty=0.1Ty=0.15Ty=0.2G1(0.5jωf)0.13430.17030.2033G2(0.5jωf)3.92334.98396.0127G3(0.5jωf)1.36191.71480.2154G1(jωf)0.08440.08450.0848G2(jωf)48.320748.516248.6285G3(jωf)0.49310.49110.4901

4结论

本文在建立的水轮发电机组非线性调速系统模型的基础上，针对传统时频方法分析的不足，提出了基于非线性输出响应模型的分析方法，对不同空载流量及不同主接力器时间常数下的水电机组调速系统进行了分析，由分析结果可知：

(1)空载流量的变化主要影响了调速系统的二阶非线性特性，其主要倍频的二阶NOFRFs值在空载流量变化时都发生了较大变化。

(2)主接力器时间常数的变化主要影响0.5倍频的各阶NOFRFs值，而其他倍频的NOFRFs值变化不大。

通过对水轮发电机组调速系统的非线性输出响应分析，其结论可为调速系统的优化控制与诊断提供一定的依据。

参考文献：

[1]方红庆， 陈龙， 李训铭. 基于线性与非线性模型的水轮机调速器PID参数优化比较[J]. 中国电机工程学报， 2010， 30(5)： 100- 106．

[2]LANSBERRY J E， WOZNIAK L. Adaptive hydrogenerator governor tuning with a genetic algorithm[J]. IEEE Transaction on Energy Conversion， 1994， 9(1)： 179- 185．

[3]邓磊， 周喜军， 张文辉. 用于稳定计算的水轮机调速系统原动机模型[J]. 电力系统自动化， 2009， 05： 103- 107．

[4]殷豪. 基于遗传算法的自适应PID型水轮机调速器研究[J]. 水力发电， 2006， 32(5)： 40- 42．

[5]姜胜， 陈启卷， 蔡维由. 水轮机调速器参数仿真寻优策略[J]. 中国电机工程学报， 2008， 28(3)： 102- 106．

[6]刘志坚， 束洪春， 于继来， 等. 一种满意控制的水轮机调速系统参数优化方法[J]. 中国电机工程学报， 2009， 29(20)： 99- 105．

[7]孙美凤， 张永华， 张俊红. 水轮机调速器参数自整定遗传算法的研究[J]. 水力发电， 2007， 33(5)： 44- 46．

[8]Group IEEE Working， Others. Hydraulic turbine and turbine control models for system dynamic studies[J]. IEEE Transactions on Power Systems， 1992， 7(1)： 167- 179．

[9]KUNDUR P. Power system stability and control[M]. New York： McGraw-Hill， 1994．

[10]方红庆， 沈祖诒. 水轮机调节系统分析[M]. 北京： 中国水利电力出版社， 1991： 7- 97．

[11]KHAN A A， VYAS N S. Application of Volterra and Wiener theories for nonlinear parameter estimation in a rotor-bearing system[J]. Nonlinear Dynamics， 2001， 24(3)： 285- 304．

[12]唐浩， 屈梁生， 温广瑞. 基于Volterra级数的转子故障诊断研究[J]. 中国机械工程， 2009， 10(4)： 447- 449．

[13]LANG Z Q， BILLINGS S A. Energy transfer properties of non-linear systems in the frequency domain [J]. International Journal of Control， 2005， 78(5)： 345- 362．

(责任编辑高瑜)

Analysis on Nonlinear Output Frequency Response of Hydro Governing System

XIA Xin1, NI Wei1, ZHOU Jianzhong2

(1. College of Automation, Huaiyin Institute of Technology, Huaian 223003, Jiangsu, China; 2. College of Hydroelectric Digitization Engineering, Huazhong University of Science and Technology, Wuhan 430074, Hubei, China)

Abstract:As the hydro turbine governing system has many nonlinear link, a method based on nonlinear output frequency response functions (NOFRFs) is proposed to apply on the analysis of governing system of hydro-generator unit. This method can avoid the problem in complex system modeling and provide good description on the nonlinear characteristics. Firstly, the nonlinear hydraulic governing system model is built. Then, the hydraulic governing system is simulated under different operation conditions and the NOFRFs under different operation conditions are identified. Finally, the nonlinear characteristics are analyzed. The simulation results indicate that the proposed method can clearly describe the change of nonlinear characteristics. The proposed method can provide some theoretical basis for optimal control and fault diagnosis of governing system．

Key Words:governing system; nonlinear output frequency response; parameter identification; hydro-generator unit

中图分类号：TM312

文献标识码：A

文章编号：0559- 9342(2016)01- 0070- 04

作者简介：夏鑫(1989—)，男，湖北荆门人，讲师，博士，主要研究方向为水力发电机组系统辨识与故障诊断．

基金项目：国家自然科学基金项目(51079057)

收稿日期：2015- 08- 15