捕捉有效样本 促进课堂动态生成
■ 武汉市蔡甸区第一小学 刘秀芬
捕捉有效样本促进课堂动态生成
■武汉市蔡甸区第一小学刘秀芬

样本是学生自己创造出来的宝贵的、有价值的教学资源。教师要有敏锐的洞察能力,对每一个样本做出及时、准确地判断,捕捉到有效的样本,促进课堂动态生成。如何捕捉有效的样本呢?我觉得应该从以下3个方面入手。
一、在备课中预设有效样本,引领动态生成
俗话说:凡事预则立,不预则废。预设是教学的基本要求,也是教学的起点。在备课中,预设有效样本与预设其他环节同样重要。教师要给自己预设的样本确立一个明确的目标,使它们成为新知生成的“催化剂”。首先我们就要搞清楚什么样的样本是有效样本。有效样本应该包括两个方面:第一、有利于突出教学重点的样本才是有效样本。第二、有利于突破教学难点的样本才是有效样本。我们只有从这两个方面精心预设了有效样本,才能在课堂上有目的地进行选择。例如:我在上人教版二年级上册《数学广角》排列前就在头脑里预设了三种样本:(一)有重复或遗漏的排列。(二)交换位置法的排列。(三)固定十位法的排列。我估计固定个位法在学生样本里不会出现,准备讲完固定十位法后提示学生。上课时,我先让学生2人小组合作:用数字卡片1、2、3摆两位数,并填入下表。接着选取了以下三个样本:

这三个样本代表了三种解题思路:第一种是无序思维,任意摆,有重复。是学生错知的暴露点;第二种是交换位置法,是新知的生成点;第三种是固定首位法,是学生有序思维的优化点。我捕捉到了三个有效样本,它们层层递进,使新的目标不断生成,学生的认识和体验不断加深,创造的火花不断迸发,新知生成就水到渠成。
反之,教师在备课时没有预设有效样本,选择了不恰当的样本就会阻碍新知的生成。例如:某老师在上人教版四年级上册《平行与垂直》时,他是这样设计的:
(一)画图感知,确定研究对象。
过渡:今天我们继续研究有关直线的知识,就是两条直线在同一平面内的位置关系。
板书:两条直线
1.想象活动
想象纸面上两条直线的位置关系。
师:想一想,如果我们在这张长方形纸上画两条直线,这两条直线会有怎么样的位置关系呢?(学生想象)
2.动手操作
学生在草稿纸上任意画两条直线。
……
教师选了如下三个样本:

师:同学们的想象力真丰富,画出了这么多种情况。根据两条直线的位置关系你能给它们分分类吗?
生:可以分两类。把第一种和第三种分成一类,第二种分成另一类。
师:有不同意见吗?
……
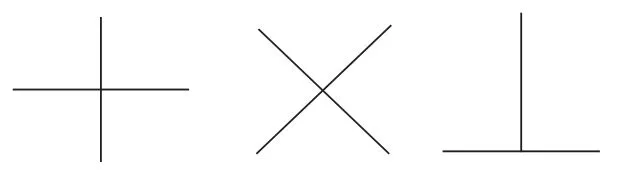
全班学生都没有反对意见。为什么呢?从直观上看,学生很容易把第一和第三放在一起。因为学生在没有学习相交和不相交的知识前,凭感觉认为第一种是不相交的。教师花了很长时间引导学生认识第一种为什么属于相交。当教师在总结时提问:在同一平面内,两条直线的位置关系是什么?还有很多学生说是垂直和平行。纵观教师的教学设计没有问题,问题出在哪?他选择的样本出现了问题。这一环节重点讲的是在同一平面内,两条直线的位置关系只有两种情况:相交和不相交。结果样本的选择上没有出现明显的相交的例子,孩子把注意力全部放在了垂直上。教学的重点出现了偏移,学生往往错误地用垂直来替代相交,用特殊代替了一般。以上样本应该做以下改动:

接着讲垂直的时候,他出示了以下三个样本:

师:这三个图形哪一个比较特殊?
生:第三个。
师:有不同意见吗?
……
学生认为第一种和第二种明显相交,第三种要延长了才能相交。所以孩子都同意第三个特殊。教师把第三个当做有效样本出示显然不妥。这样把学生的注意力转移到了相交上。垂直必须具备两个要素:①两直线相交。②相交成直角。但在前面已经重点学习了相交,这里探究的重点是第二个要素:相交成直角。我觉得样本要做如下改动:
总之,我们备课不仅要备学生、备教材还要备样本。只有做到心中有数,教师才能顺利捕捉到有效的样本,引领课堂动态生成。
二、在探究中丰富有效样本,促进动态生成
有效样本的产生,离不开教师精心设计的教学环节,更离不开一个开放式的教学探究活动。条条框框少了,学生的思维才会活跃起来。困难生会充分暴露知识的错误点,引发学生思维的碰撞。例如:在学习人教版五年级上册《梯形的面积》时,由于学生已经经历、探索了平行四边形和三角形面积计算的推导过程,并形成了一定空间观念。于是我设计了一个开放式的探究活动:让学生4人小组动手剪一剪、拼一拼、画一画、折一折把梯形转化为已学过的各种图形。并提出操作和探究的要求:转化后是什么图形?转化后图形的面积会不会计算?转化后图形的面积与原来梯形的面积有什么关系?以下是孩子们创造出来的样本。


如果把以上样本都用来推导梯形的面积公式,显然是不合适的。我引导学生捕捉有效样本。
师:你觉得哪些样本可以合并成一种来探究?小组内可以议一议。
生:我觉得可以把第1种、第2种和第3种合并成一种。正方形和长方形是特殊的平行四边形。
生:这些梯形的面积都可以用一个平行四边形的面积加一个三角形的面积来计算,我们可以选择第一种为代表。
师:你觉得还有哪些样本也可以合并?
生:第5、6、7种也可以合并成一种。只有2个一样的直角梯形可拼成正方形或长方形,具有特殊性。我们选取第5个为代表进行研究。
……
学生通过讨论、交流把9个样本浓缩成了5个,接着让学生选择自己喜欢的样本推导梯形的面积公式。汇报如下:
方法一:(分割)
1.把梯形分割成一个平行四边形和一个三角形

梯形的面积=平行四边形的面积+三角形的面积
=上底×高+(下底-上底)× 高÷2
=上底×高+下底×高÷2-上底×高÷2
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
2.把梯形分割成两个三角形

梯形的面积=三角形的面积+三角形的面积
=上底×高÷2+下底×高÷2
=(上底+下底)×高÷2
方法二:(拼组)
把2个一样的梯形拼成一个平行四边形。

梯形的面积=平行四边形的面积÷2
=底×高÷2
=(上底+下底)×高÷2
方法三:(割补)
1.把一个梯形剪成两个高相等的梯形再拼成一个平行四边形
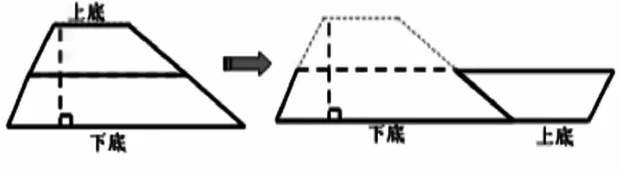
梯形的面积=平行四边形的面积
=(上底+下底)×高÷2
2.把梯形剪成两个三角形和一个六边形再拼成一个长方形
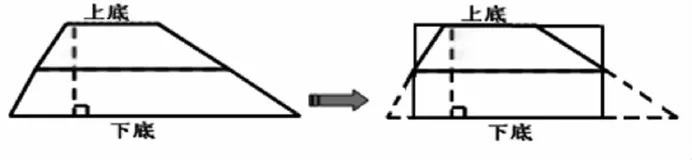
梯形的面积=长方形的长×宽
=(上底+下底)÷2×高
=(上底+下底)×高÷2
我提供给学生的学具是开放的:有直角梯形、等腰梯形和普通梯形。让孩子们自己选择。探究的过程是开放的:学生可以任意选择画、剪、折、拼等活动方式探索把梯形转化成学过的任意图形。其中第8个样本就是学生动手折出来的。样本的展示是开放的:几乎把孩子设计的不同样本都展示出来了。选择有效样本的形式也是开放的:在教师引领下,通过孩子议一议,选择出5个有效样本。接着让学生选择自己喜欢的样本推导梯形的面积公式,最后汇报交流。在平等、愉悦的氛围中,学生们的智慧在合作中激发,不同的思维在探究中碰撞。正所谓:水本无华,相荡乃成涟漪;石本无火,对击始发灵光。课堂变成了一幅真实、自然生成的画卷。
三、在追问中完善有效样本,演绎动态生成
新课标重视课堂预设,更重视课堂的生成。再高明的教师也不可能把一节课的有效样本全部设计出来。更何况在目前的网络时代,学生的信息量不断增长,创新意识不断加强,他们解决问题的方法也异彩纷呈。教师及时有效地追问能产生意想不到的样本。例如:我在上人教版五年级《长方形的表面积》时选取了两个样本如下:
长方体的表面积=长×宽×2+ 长×高×2+宽×高×2
长方体的表面积= (长×宽+长× 高+宽×高)×2
我确信没有其他的方法,但我还是习惯性地追问了一句:你还有其他做法吗?一个孩子很坚定地说:“有”。他的答案是:
长方体的表面积= (宽+高)×2× 长+高×宽×2
面对全班学生迷惑不解的眼神,我让学生说明理由。原来他把长方形展开后如下图:
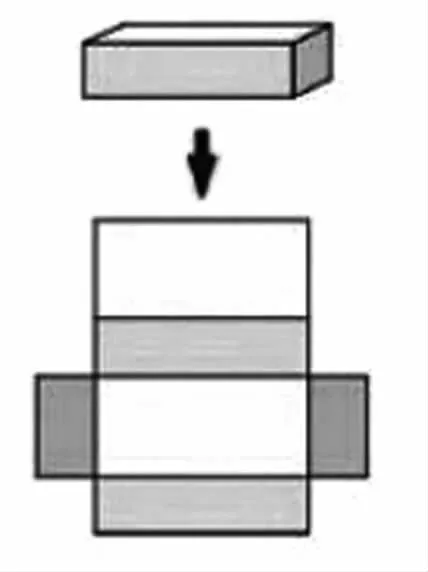
原长方体的(宽+高)×2是展开后中间大长方形的长,原长方体的长是展开后中间大长方形的宽。所以(宽+高)×2×长是求的展开后中间大长方形的面积。原长方体的高×宽×2求的是展开后两边的小长方形的面积和。追问——捕捉到了创新的样本,独特的思维;追问——成就了“无心插柳柳成荫”的惊喜。正如教育家布鲁姆说:“人们无法预料到教学所产生的成果的全部范围。如果没有预料不到的成果,教学也就不能成为一种艺术。”
综上所述,只有精心预设有效样本,才能使教师捕捉样本有方向,有目标,教学才不会偏离航道;只有让学生充分探究,才能丰富有效样本,激发学生思维;只有适时追问,才能引出精彩纷呈的解题方法,造就“横看成岭侧成峰,远近高低各不同”的精彩画面。
责任编辑郑占怡

