考试作弊行为的博弈分析及对策研究

李恒祥 李一鸣 李姗姗（河北农业大学商学院 河北保定 071000）

考试作弊行为的博弈分析及对策研究

李恒祥 李一鸣 李姗姗（河北农业大学商学院 河北保定 071000）

在我国绝大部分高校中存在着考试作弊的不文明行为。各大高校采取了各种措施，但还是屡禁不止，作弊不仅是小范围的不文明现象，更是影响着整个学校的公平竞争氛围。大学生是社会的未来，大学时期不遵守考场纪律，也会对社会诚信、契约精神产生深刻的不良影响。本文采用了博弈论的视角分析考试作弊风气形成的原因，并对这一现象提出具体解决方案。

作弊；博弈；对策

一、引言

在高校中，考试成绩是衡量学生的学业学习成果和教师教学水平的主要指标，也是评奖评优，入党，推免研究生，出国读研的重要甚至是主要标准。正因为这个指标对学生来讲十分重要，所以也滋生了不公平竞争的作弊行为。目前各大高校的考风普遍比较恶劣，尤其是高年级的作弊现象更是突出。而在这种严峻的态势下，没有高校出台的规定对这种不正当竞争行为有有效的遏制作用。这种现状既影响了评奖评优指标的可靠性，又不利于学生的公平意识和契约精神教育。故考试作弊问题已经成为了学校管理部门和社会各界重点关心的问题之一。

通过微观经济学的知识可知，在完全竞争市场的前提下，每个经济人都会做出最理性的选择，在每个经济人做出最优选择的同时，整体达到帕累托最优，任何一方不能获取超额利润。但是在学校的期末考试中，各个学生之间信息不对称，经过博弈之后选择对自己平均效用最大的决策，但是这并不是整体最优决策。

二、作弊分类

按照作弊的目的不同而将作弊分成两类：通过性作弊和争优性作弊。这两种博弈在博弈分析和治理方法上都有所区别。

1.通过性作弊

在此定义的通过性作弊是指为了通过本次考核的最低限制而采取的作弊行为。

2.争优性作弊

在此定义的争优性作弊是指为了获得考试成绩优秀获得的奖励、荣誉等而采取的作弊行为。

三、简单博弈分析

1.囚徒困境

两个共谋犯罪的人被关入监狱，不能互相沟通情况。如果两个人都不揭发对方，则由于证据不确定，每个人都坐牢一年；若一人揭发，而另一人沉默，则揭发者因为立功而立即获释，沉默者因不合作而入狱五年；若互相揭发，则因证据确实，二者都判刑两年。

图一

囚徒困境关键在于由于信息不对称造成的个人利益与集体利益相冲突，由图一可知，无论对方选择坦白与否，自己若选择坦白则一定比不坦白所判处刑期要少，所以博弈的结果是都选择坦白。这是一个占优策略，即无论对方的选择是什么，自己选择坦白总比选择不坦白收益要高。

2.通过性作弊简单博弈与混合策略

通过性作弊的特点是单方面的，和其他人作弊与否无关。设是否作弊的激励因素临界值为，受多种因素影响：对自己不能通过考试的焦虑程度，公正监考的严厉程度，其他正面激励因素。所以：时是学生选择是否作弊的临界点。

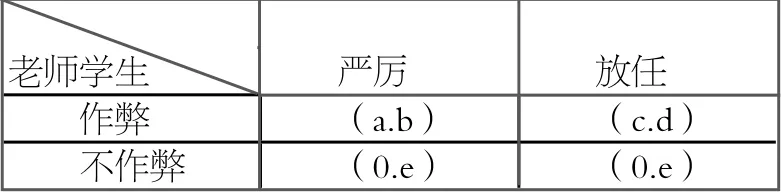
其中abcd为老师或学生从本次考试中获得的效用。其大小关系为b＜a＜c＜0＜d，e＜0。abd都是负面效用。b为作弊被老师查处后学生所面临的严厉处罚（留校察看开除学籍等），a为因为给学生带来了严厉处罚而给老师带来的负面效用，d为作弊后分数提高而给学生带来的正面效用，c为放任此学生作弊破坏公平公正给老师带来的负面效用，e为有可能不通过考试的焦虑和诚信考试的自豪感总和。

因为b为一个极小的值而导致a也非常小，假设老师严厉的概率为，放任的概率为。学生作弊的概率为，不作弊的概率为。

可见因为a＜c所以E（X）＜。出于个人利益最大化的原则，通

作弊学生的平均效用为

E（Y）=

所以E（Y）＞E（ ）

从这次博弈分析中可以看出老师倾向于不严厉监考而学生倾向于作弊，即（放任.作弊）。这是一组纳什均衡，即给定一方的选择，则另一方的选择一定是最优的。

3.争优性作弊简单博弈的占优策略

争优性作弊的目的是争取更好的排名，而不是通过考试。又因为前文已经分析过老师放任的可能性趋近于1，所以在此只涉及和其他同学之间的博弈。假设丙丁两同学水平相当，作弊手段相当，在同样的考试环境下进行考试，且在考试前双方都不知道对方是否会作弊。博弈收益矩阵如图二。

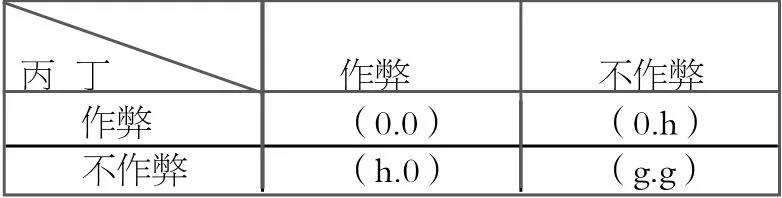
图二

只要有一方成功作弊而另一方没有作弊的话，在本次博弈中就会取得优胜，但是会背负不诚信考试的负罪感和作弊被发现和处罚的风险。因博弈优胜的效用远远大于风险，所以h＞0.若双方都作弊，则对自己的排名没有明显提高，但是背负上了不诚信考试的负罪感和作弊被发现和处罚的风险。，同时取得卷面上较高的分数，故效用为0。若双方都不作弊，则是一个公平竞争诚信考试的环境，故g＞0且0＜g＜h。

当丁选择作弊时，丙选择作弊的效用为0，不作弊的效用为0.0=0

当丁选择不作弊时，丙选择作弊的效用为h，不作弊的效用为g.g＜h

从这次博弈中可以看出，（作弊.作弊）是一个占优策略，即无论对方选择什么，选择作弊的效用总是大于不作弊的效用，所以纳什均衡的结果是双方都选择作弊，这是理性的选择。很明显当双方都不作弊的时候整体达到最优，而且，当得知对方会采取作弊行为时，己方一定会采取作弊来保证自己的利益。当不知道对方是否作弊时，会选择作弊。

四、重复博弈

根据博弈论来讲，一次博弈、多次博弈和无限次博弈的结果会有所不同。从分类来看，通过性作弊的重复博弈和争优性重复作弊博弈又有所不同。

1.通过性作弊重复博弈

由于每次考试的监考老师都不相同，而且即使重复间隔时间也都比较长，重复次数少。所以假设每次考试都面对不同的监考老师，即每次的博弈都相当于一次博弈。和前文2.2中分析的结果一样，每次的均衡策略都是（放任.作弊）

2.争优性作弊重复博弈

争优性作弊重复博弈与通过性作弊重复博弈不同，大学期间所有的考试基本都是和同专业的同学竞争，而水平相当的同学不会变化太多，所以争优性作弊重复博弈分析的博弈对手是同样的人。

（1）无限次博弈

若是无限次考试，假设第一次考试中丙、丁选择的结果是（作弊，不作弊），且双方在考试中都知道了对方的选择。则在下一次考试中丁就可以选择“作弊”来惩罚丙，届时，不管丙选择哪种行为其收益都将是0。丙会意识到如果长期收益为0时收益会较（不作弊.不作弊）选择的收益g大幅减少，所以丙就会选择“不作弊”。

那么在无限次博弈中这种策略收益是不是最高呢？密歇根大学的政治科学家罗伯特·阿克塞尔罗德曾经在一系列的实验中用令人信服的方法证明了这一论点。他要求几十名博弈论专家为囚徒困境的重复博弈提出他们最中意的策略，然后，他在计算机上演示‘巡回赛’，使这些策略相互竞争。每个策略在计算机上都要和其他的所有策略进行比较，并且计算机会记录下全部策略的收益。

胜出的策略——具有最高总收益的策略——结果证明是最简单的策略。这种策略称为“针锋相对”，即在每一局，你都要采取对手在上一局所选择的策略。

所以，实验显示，这种策略，惩罚措施是有效率的。

（2）有限次博弈

从现实来讲，考试的次数总是有限的，和同一个人竞争更是有限的。我们不妨从最后一次博弈分析起，最后一次博弈相当于一次博弈，所以最后一次考试的均衡策略为（作弊.作弊），既然最后一次博弈的结果已经知道，倒推倒数第二次博弈也没有必要保持（不作弊.不作弊）的合作，倒推倒数第三次、倒数第四次，一直到第一次。其均衡策略都是（作弊.作弊）。

所以只要博弈次数（考试次数）是有限的，双方就不会达成（不作弊.不作弊）的互利合作，而是一直选择作弊作为自己的策略。

五、序贯博弈

之前我们所考查的博弈中两个参与人都是同时采取行动的。但是在许多情形下并不是同时决策，而是一方首先采取行动，另一方再作出反应。在这样的博弈中，先进行决策的参与人是领导者，后进行决策的参与人是追随者。如在通过性作弊博弈中，进行博弈的老师可能已经惩罚过一个作弊的学生，这将使在博弈的学生有理由相信这个老师已经选择了严厉。相反，该学生已经看到老师已经看到别的学生在作弊却没有对其进行惩罚，这个表现使学生有理由相信老师选择了放任。

1.通过性作弊序贯博弈

（1）老师为领导者

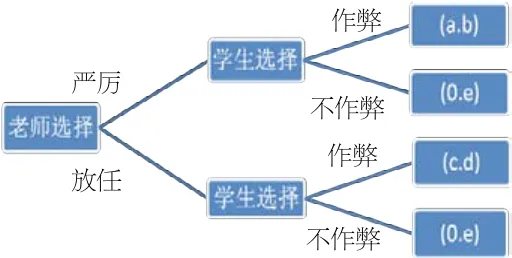
当已知老师选择“严厉”策略时学生选择“作弊”时效用为b，“不作弊”时效用为e。由于b＜e，所以可以预料学生一定会选择“不作弊”。所以均衡为（严厉，不作弊），老师的效用为a。

当已知老师选择“放任”策略时学生选择“作弊”时效用为d，“不作弊”时效用为e。由于e＜b，所以可以预料学生一定会选择“作弊”。所以均衡为（放任，作弊），老师的效用为c。

由于老师预料到了自己选择的均衡结果，又因为a＜c,所以老师一定会选择（放任，作弊）这一均衡。

（2）学生为领导者

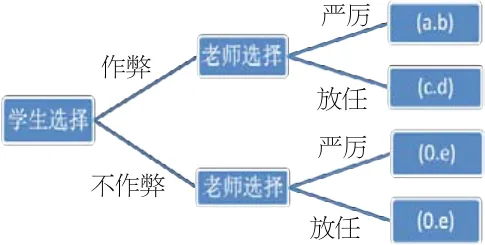
当已知学生选择“作弊”策略时老师讲选择“严厉”时效用为a，“放任”时效用为c。由于a＜c，所以可以预料老师一定会选择“放任”。所以均衡为（放任.作弊），学生的效用为d。

当已知学生选择“不作弊”策略时老师讲选择“严厉”或“放任”时效用都为0，而且学生也知道只要他选择“不作弊”，均衡效用一定是（0.e），所以没有任何区别。

因为d＞e，所以学生一定会选择“作弊”，最后的均衡仍然是（放任，作弊）

2.争优性作弊序贯博弈

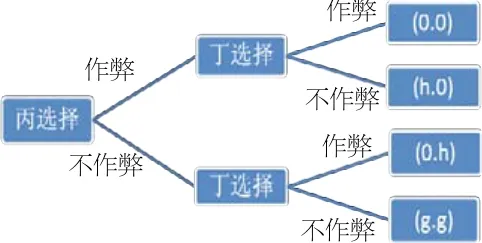
当已知丙选择“作弊”策略时丁讲选择“作弊”和“不作弊”时效用均为0。但是选择“不作弊”时博弈会失败，所以均衡为（作弊.作弊），丙的效用为0。

当已知丙选择“不作弊”策略时丁讲选择“作弊”时效用为h，“不作弊”时效用为g。由于g＜h，所以可以预料丁一定会选择“作弊”。所以均衡为（不作弊.作弊），丙的效用为0。

但是，丙可以预料到如果他选择不作弊，则在本次博弈中一定会失败，即考试成绩低于丁，所以处于领导者地位的人一定会选择“作弊”作为自己的策略。反之亦然。

六、治理对策

对于作弊行为的治理，显然采取常规的思想教育，签保证书，宣誓等传统方法效果并不显著，因为这种措施并没有真正意识到作弊的目的和对作弊采取分类治理的必要性。下面本文通过以下几个方面对作弊行为治理提出建议。

1.降低处罚力度，加快惩罚速度

法学泰斗贝尔卡利亚说过：“法律的威慑力，源于承担犯罪后果的必然性，而非承担后果的严重性”。所以上文已经分析过老师在选择严厉是所付出的心理成本太高，在学生作弊时老师的效用为a，a是一个极大的负数。简单来说就是对学生的仁慈，不忍心看到学生付出高昂的作弊成本。所以第一个措施就是降低老师在处罚作弊学生的心理成本。可以采取当老师发现学生作弊后可以酌情申请：重修、重修且缴纳重修费用、警告、记过、留校察看、开除学籍等处分，并说明原因。这样既可以保证公平竞争，又不至于对作弊者处罚过重，从而导致了制度执行率不高的现象。

2.注重平时作业

无论平时作业是不是纳入综合评分标准都要重视平时作业。其原因在于平时作业是对阶段性学习成果的考量。可以从作业中看出学生是否从课程中学到了知识，并且可以在平时监督学生认真而全面的学习，从而减少学生在考试之前的焦虑程度，减少其作弊概率。

也可以让学生作业中发表自己的看法。而且从平时作业中较容易发现抄袭行为，从而对学生进行警告或处罚，避免考试作弊而面临的更严重的处罚。

3.将发现作弊定入年终奖金评定标准

此项措施也是提高老师采取严厉措施时的效用，让老师愿意惩罚破坏考场纪律的人，维护考试公平。不仅要减少老师查处作弊的负罪感，也要提高物质奖励。

4.利益不相关者监考

有些老师存在“直系学生”的概念，即使处罚力度小，有物质奖励，也出于维护学生的角度考虑不愿意处罚学生，尤其是在平时跟老师关系比较好的学生。所以可以从其他院系安排老师交替监考，这样可以避免老师袒护，从而导致的不公平竞争。

5.重点监考

因成绩优异者的作弊是想要获得学校对优秀学生的奖励等有限资源，所以更要对成绩优秀学生的作弊严加监督。在考试前可以在在上一次考试中成绩较为优异的学生桌子上放置优秀学生标志。通过监考老师严格监考来避免争优性作弊，以不正当方式来获得有限资源的行为。

6.在确保监考有效的同时采取较为严厉处罚

这项措施与通过性作弊防治的降低处罚力度并不冲突，这里指的严厉处罚是指对优秀学生而言的严厉处罚。如一次作弊四年禁止入党，禁止评奖学金，禁止本系教授为其写出国推荐信，本科成绩记不及格等对于争优性作弊的严厉措施。提高其作弊平均成本，从而防止其作弊。

七、结语

此前所做分析均为在学生和老师完全理性的假设前提之下，实际中情况并非完全如此，影响因素有很多，诸如学生素质、家庭教育、老师的教育理念等。但是本次博弈分析也显示出了学生和老师对（放任，作弊）和（作弊，作弊）的倾向。也提示了我们应该从老师和学生自身的利益出发，对规则进行修改，使其自发选择“严厉”和“不作弊”，而不是靠道德约束。从而使高校的考试作弊现象有所减轻，营造公平公正的竞争氛围。

[1]哈尔·R·范里安.微观经济学现代观点[M].格致出版社·上海三联书店·上海人民出版社.2011年2月第一版

10.19312/j.cnki.61-1499/c.2016.02.064