基于Monte Carlo模拟的巨灾风险债券定价研究——以中国洪水巨灾债券为例

黄英君，李江艳，韩经纬(重庆大学经济与工商管理学院，重庆400030)



基于Monte Carlo模拟的巨灾风险债券定价研究——以中国洪水巨灾债券为例

黄英君，李江艳，韩经纬
(重庆大学经济与工商管理学院，重庆400030)

摘要:近年来各类灾害统计数据显示我国已成为世界上受洪涝灾害影响最为严重的国家之一。如何在有效防范洪涝灾害的基础上对其所造成的损失进行最大限度最为有效的弥补也成为各界关注的主要问题。在对现行巨灾风险管理工具进行不断尝试的过程中，巨灾风险债券因其投资风险相对较低、投资收益相对高的特性，成为了目前衔接保险市场与资本市场最为有效的巨灾风险管理工具之一。基于此，本文一方面试图探索巨灾风险债券作为一种新型巨灾风险管理工具在我国开展的必要性及可行性;另一方面通过对我国洪涝灾害损失数据进行分析，并试图运用非寿险精算原理及资本资产定价模型对我国洪水巨灾风险债券定价研究进行初步探索。

关键词:巨灾风险债券定价; Monte Carlo模拟;洪水巨灾风险债券

1　引言

近年来，随着地震、洪水、海啸等自然灾害的频发，世界性的灾难日益严峻，其所造成的直接经济损失和遇难人数也在不断剧增。根据瑞士再保险2015年最新一期研究报告显示，无论是从自然灾害还是人为灾害的角度，全球巨灾的发生次数、造成的遇难人数以及所造成的保险损失都呈上升趋势，其中遇难人数以及所造成的保险损失更是居高不下。我国作为一个领土广阔、地势复杂多变的国家，遭受自然灾害风险的几率及相应损失也会大得多。现阶段，我国巨灾风险分散机制的构建均是在政府主导下，保险公司与再保险公司共同参与，而庞大的巨灾损失，使得保险公司无力继续承保巨灾保险及再保险，只能通过政府财政救济手段来分散巨灾风险。但仅通过政府救济来分散巨灾风险显得过于单一，且相对于巨灾风险所造成的巨大损失，政府财政救济金明显不足以弥补。因此，在政府对于巨灾风险损失进行直接补偿的同时，需要有其他的巨灾风险分散方式与其并行。对于巨灾风险基金而言，因其具有庞大资金基础，若能顺利开展亦能有效分散一部分巨灾风险。但我国的巨灾风险基金目前还处于起步阶段，从设立、运行到监管均较为复杂，且需要一个较长的周期。因此，亟需在传统型巨灾风险管理工具基础之上，寻找一种新型的能够提供巨灾资金支持的巨灾风险管理工具以应对巨灾事件所造成的损失。此时，巨灾风险证券化作为一种新型的巨灾风险管理模式开始出现，其通过将保险市场与资本市场进行有机结合达到资本市场向保险市场提供强有力资金支持，保险市场则向资本市场提供更高的投资收益的目的。这一新型的巨灾风险管理模式，一方面解决了传统巨灾风险管理工具巨灾保险、巨灾再保险等所无法解决的资金问题，另一方面也增加了资本市场的流动性，开始逐渐被推行。

国外学术界关于巨灾保险证券化的研究始于上世纪90年代。在当时金融证券化和保险金融化的大背景下，Goshay和Sandor［1］首先提出了保险衍生品的概念，他们提出将保险市场和资本市场连接起来，将保险和再保险市场的风险转移到资本市场上去。随后各类学者开始针对各类巨灾保险证券化产品的可行性进行了研究，如Kunreuthe和Pauly［2］对巨灾债券的运行机制可能存在问题进行了研究; Froot［3］则进一步对巨灾债券可行性进行分析，并指出巨灾债券能够成功运行的原因。在巨灾保险证券化产品逐渐得到学术界认可后，学者们开始对巨灾保险证券化产品的定价问题进行研究，其中包括Lane［4］通过对已发行巨灾债券参数进行回归分析后所提出的LFC定价模型; Lin和Cox［5］对在死亡率基础上的保险证券化产品定价模型进行了研究，并根据该模型诠释了存在两个纯死亡率保险债券产品的不同收益; Chang等［6］利用无套利定价模型对亚式巨灾期权进行的定价等。

目前，我国学术界针对各类巨灾风险证券化工具所展开的研究较多集中于对巨灾风险证券化种类，运行机制等相关情况的研究。如施建祥和邬云玲［7］提出巨灾风险证券化结合了资本市场与保险市场，且保证了保险市场的安全、高效运行，其通常包括巨灾互换、巨灾期权、巨灾风险债券等多种形式。田玲和张岳［8］提出对于巨灾风险证券化工具的定价也就意味着对金融市场和保险市场的统一定价，具有重大意义。庹国柱等［9］对各类巨灾风险证券化工具的实际发行情况等数据进行收集整理，发现在所有巨灾风险证券化工具中巨灾风险债券的发行量和成交量所占比重最大，约占巨灾风险证券市场的一半份额。除此之外，也有学者对巨灾风险证券化工具的定价问题进行研究，但相对而言较少。如韩天雄和陈建华［10］运用了均衡定价理论［11］给出了巨灾证券产品定价的表达式。田玲和向飞［12］比较分析了巨灾风险定价框架下各类模型，LFC模型［4］、Wang的两因素模型［13］和Christofides模型［14］等的优缺点及适用条件等。施建祥和秦倩琪［15］则利用非寿险精算技术、资本资产定价模型和债券定价原理分析计算我国台风灾害债券的收益率和价格。李永和范蓓［16］结合无套利BDT利率期限结构模型建立了我国巨灾债券短期利率离散形式的动态变化模型。谢世清和梅云云［17］以保险精算角度对目前存在的主要巨灾债券定价理论模型进行了系统性分析，并提出各类定价模型的适用性等。韦勇凤等［18］通过对金融危机前后期间巨灾债券对资本市场投资组合的影响进行了实证分析，并得出巨灾债券能够有效扩展资本市场投资组合结论。翁成峰等［19］以我国地震巨灾债券为研究对象，并尝试对我国地震巨灾债券进行参数化定价研究。此外，韦勇凤等［20］运用Wang的两因素巨灾债券定价模型对公私合作下的地震巨灾债券定价进行了研究。

值得注意的是，现阶段各类巨灾风险证券化工具均处于推行阶段，具体挑选运行何种巨灾风险证券化工具，以及如若推行如何定价等问题均无统一标准。因此，在运行巨灾风险证券化工具之前，对其运行的可行性及如若运行如何定价等问题进行探究具有重大意义。本文将沿此思路进行相应研究，首先探索作为巨灾风险证券化主要形式之一的巨灾风险债券在我国运行的可行性及必要性，其次在此基础上以洪水巨灾风险债券为例，对我国洪水巨灾风险债券定价问题进行初步探索。

2　数据选取与数据处理

在本文中，我们所收集的洪水巨灾损失数据均是最为原始的数据。经过整理后得出的是某一损失范围之内洪水巨灾的发生次数及频率等。通过我们所整理出的频率数据对其进行拟合，从而得出洪灾损失所服从的分布。

2.1洪灾损失的分布拟合

本文选取的数据为直接经济损失超过1亿元人民币的灾害损失数据作为随机样本，根据洪灾损失的原始数据，我们可以得到洪灾损失的发生频率和频数分布以及洪水损失数据统计分析表。

从表1中可以看出，损失灾害数据出现分布不均的情况，在1～10亿元区间内累积频率出现迅速攀升的情况，这将会大大增加误差的出现。为了减少误差，我们对样本数据进行对数变换。同时，在对选取数据进行描述性统计分析的过程中，我们发现所收集洪水损失数据分布是正偏斜的，并且分布较为平坦。故此处假设所选取数据所服从分布为对数正态分布，其均值和方差分别为2.603201和1.992059。

为对此假设进行验证，此处我们用Monte Carlo模拟进行分布拟合。首先在MATLAB中生成一个伪随机数，并且该伪随机数服从均值和方差分别为2.603201和1.992059的对数正态分布，若该伪随机数处于样本损失数据区间内，则输出结果为1，否则为0。重复以上过程N次，在本文中假设N =10000，计算所有输出结果的总和，并将所有输出结果的总和计入输出变量SUM中，从而可以得出各不同损失区间内的拟合值“SUM/N”，结果如表1所示。

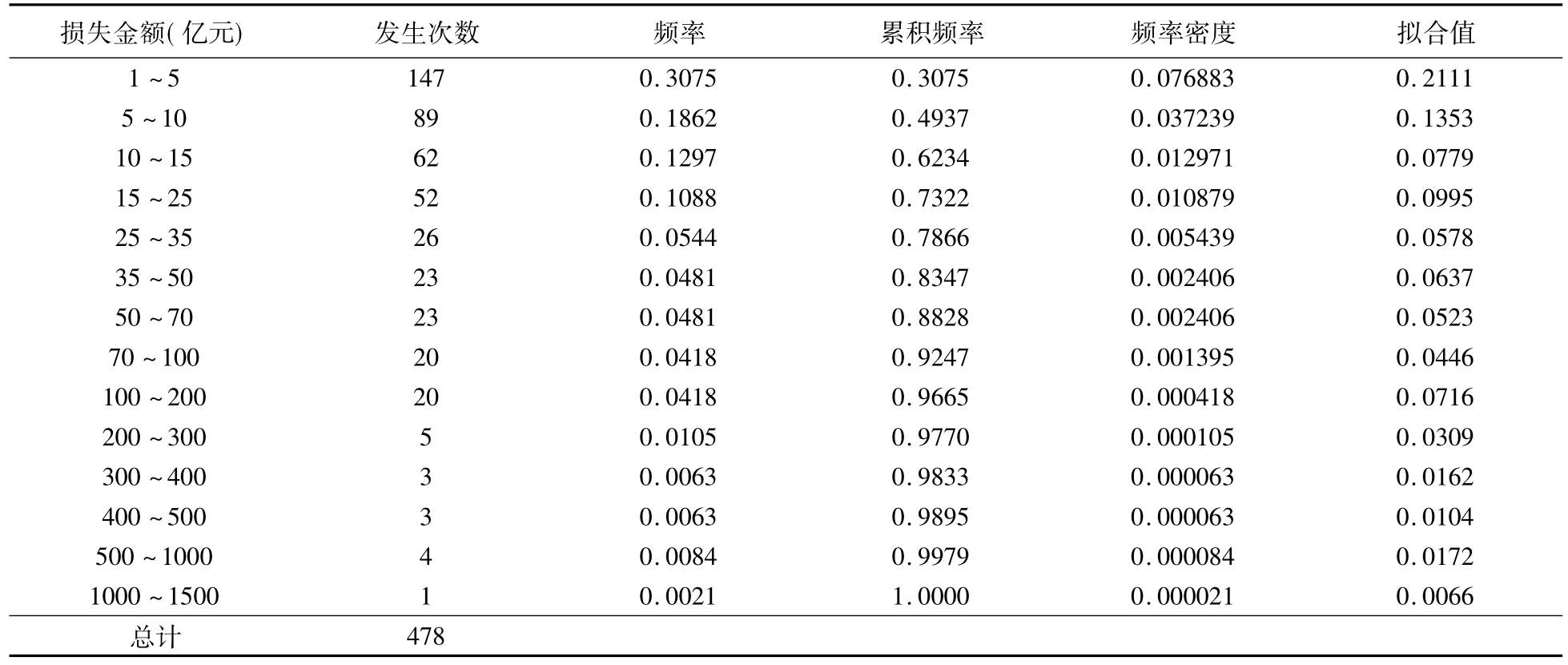
表1　我国洪水灾害损失原始数据及损失程度拟合值(1986～2014年)

在表1中，通过观察各损失程度下的拟合值，发现实际洪水损失金额的分布得到验证。因此，可以得出本文所取洪灾损失服从对数正态分布，其中μ为洪灾损失数据的均值，σ2为洪灾损失数据的方差。即

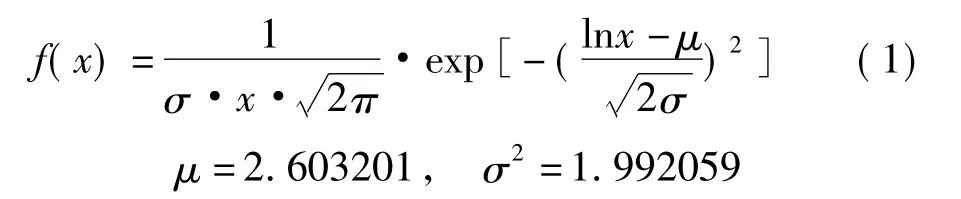
2.2洪灾损失次数的拟合

假设我国洪涝灾害发生次数服从参数为λ泊松分布，其概率分布函数为

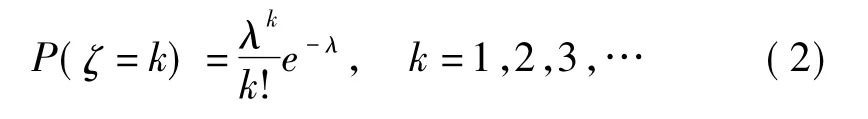
在泊松分布中，参数λ的值为洪灾发生次数的均值，运用矩估计λ= E(Y)，此时根据表1中的原始数据可得洪涝灾害发生次数的均值为18.3846。因此，在本文中λ的值为18.3846。将λ的值代入泊松分布函数，即可求出每年洪灾发生次数的概率。即

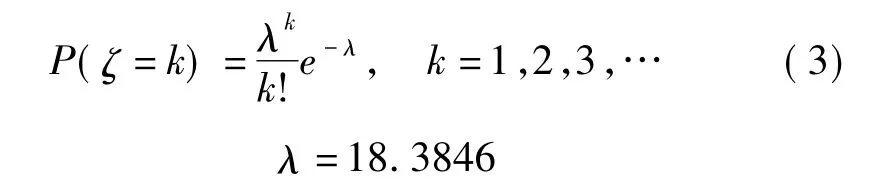
3　实证分析

洪水巨灾债券属于巨灾债券的一种，因此和巨灾债券一样，也具有相应的原始发行人，即保险公司或再保险公司;对外发行人SPV(特殊目的机构)，通常为再保险公司;以及相应的触发机制。在SPV对外发行巨灾债券时都会设立触发条件，当巨灾事件发生时，若巨灾损失超过所设立触发条件，则投资者会损失部分或全部的本金及利息;反之，若巨灾损失未超过所设立触发条件，则投资者将得到本金及相应的利息。因此，在本文中假设研究对象为期限为一年的洪水巨灾债券，其收益率记为R，触发条件为M(本文中假设洪水巨灾保险的覆盖率为30%，因此M也设定为洪水灾害年损失的30%)，实际巨灾损失达到触发条件M的概率为p。

3.1洪水巨灾债券收益率的确定

在此处，我们可以用与上文同样的方法通过Monte Carlo模拟来计算不同触发机制下的概率p。因此，如前文所示，首先在MATLAB中建立一个伪随机数记为n，且n服从参数为18.3846的泊松分布;其次建立n个伪随机数，且这些伪随机数均服从均值和方差分别为2.603201和1.992059的对数正态分布，计算这些伪随机数之和并且取其总和的30%，若该值超过M，则输出结果记为1，否则记为0。重复上述过程N次(本文中选取N = 10000)，随后将所有输出结果之和记为SUM，因此我们可以在最后得出p = SUM/N。选取不同的M，我们可以得到不同的概率p，如表2所示。

表2　不同损失金额的触发值及其触发概率

对于不同类型的巨灾债券将会有不同的触发条件，因此，本文选取(600，0.1805 )，(900，0.0888)，(2700，0.0101)三个点分别作为本金完全保证型巨灾债券、本金50%保证型巨灾债券、本金无保证型巨灾债券三种巨灾债券的触发点。

本文中，洪水巨灾债券收益率的计算公式根据资本资产定价模型来确定，即为

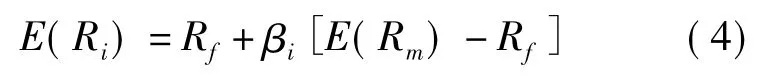
其中E(Ri)表示某金融资产的期望收益率，Rf表示无风险收益率，βi表示该金融资产的贝塔系数，E(Rm)表示市场组合的期望收益率。并且本文中假设，无风险收益率Rf为4%，市场组合的期望收益率E(Rm)为12%，洪水巨灾债券的贝塔值为0.5，则不同类型的洪水巨灾债券的期望收益率为:

(1)本金完全保证型洪灾债券(即若洪灾发生收益率为0)。

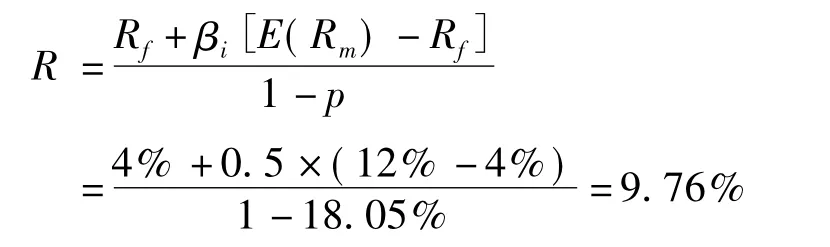
(2)本金50%保证型洪灾债券(即若洪灾发生收益率为－50%)。

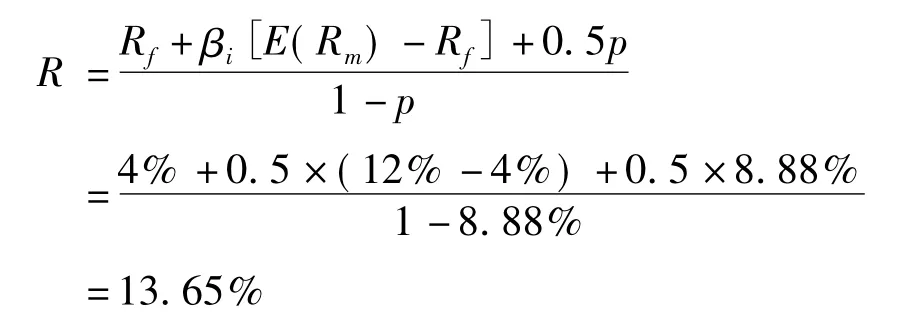
(3)本金无保证型洪灾债券(即若洪灾发生收益率为－100%)。

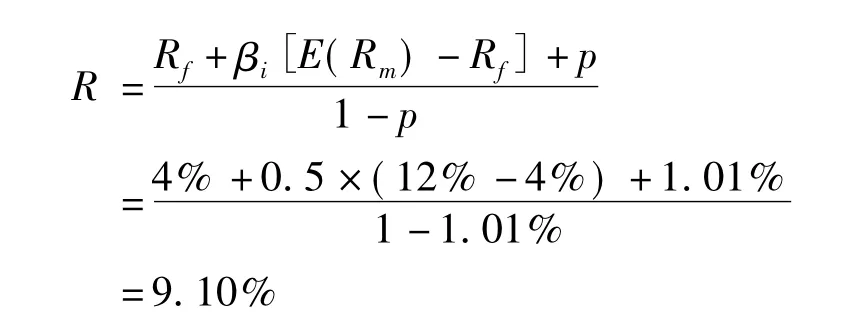
3.2洪水巨灾债券价格的确定

此处假定本文所研究洪水巨灾债券面值为100元，若巨灾灾害发生，投资者将根据洪水巨灾债券约定进行相应的债息或本金支付;反之，若巨灾灾害未发生，则该债券于每期末将支付利息i元，并在最后一期期末(T)偿还本金。假设支付函数为f，此时债务结束。用τ表示巨灾发生时刻，若在到期前巨灾发生，则τ∈{ 1，2，…，T}。则该债券的现金流［21］可表示如下

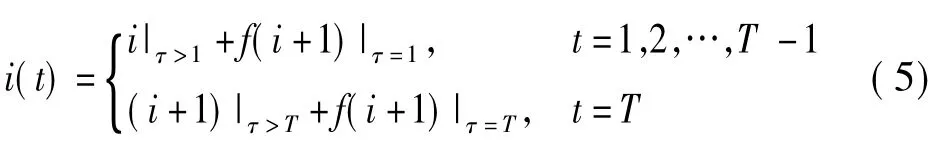
因此，在t =0时刻的债券价格P可表示为未来现金流的现值

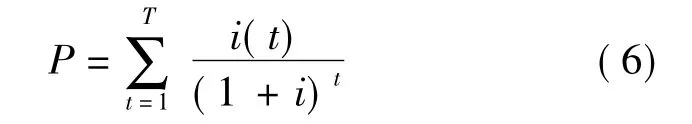
而在本文中假定发行的洪水巨灾债券为面值100元，期限为一年的债券，且每6个月付息一次。因此，需要对其进行两期现金流现值分析。假定发行为面值100元的两期洪水巨灾债券，则不同类型洪水巨灾债券的价格为:

(1)本金完全保证型洪水巨灾债券，其年收益率为9.76%，触发点为(600，0.1805)。

第一期预期收益现值

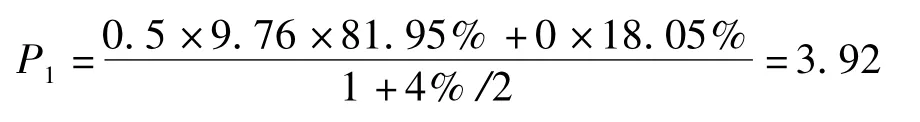
第二期预期收益现值

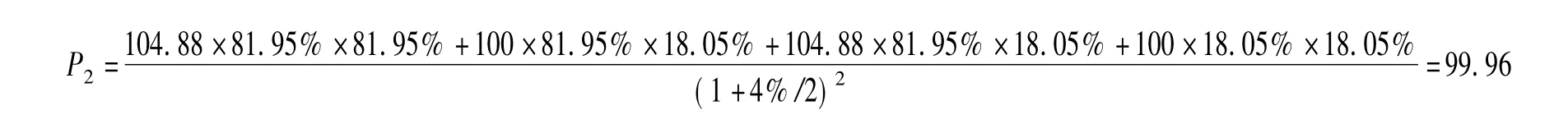
则该种类型洪水巨灾债券的价格为

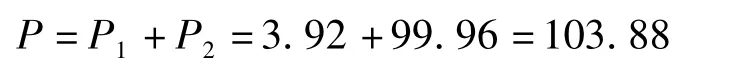
(2)本金50%保证型洪水巨灾债券，其年收益率为13.65%，触发点为(900，0.0888)。

第一期预期收益现值

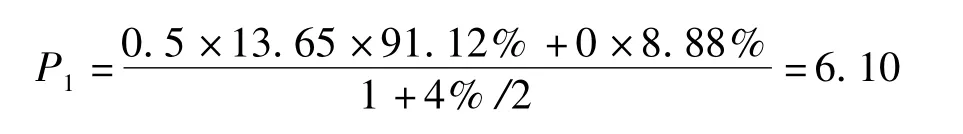
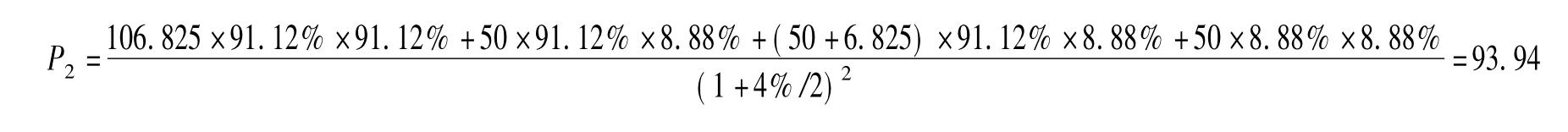
第二期预期收益现值则该种类型洪水巨灾债券的价格为

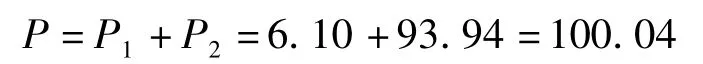
(3)本金无保证型洪水巨灾债券，其年收益率为9.10%，触发点为(2700，0.0101)。

第一期预期收益现值

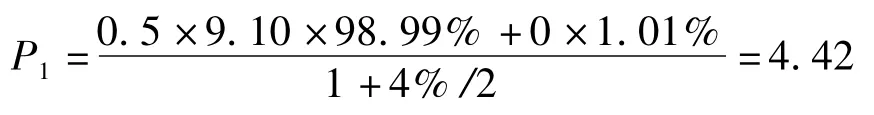
第二期预期收益现值

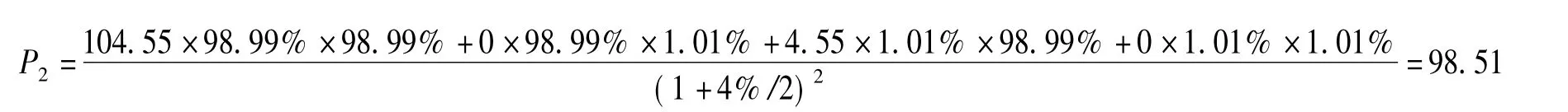
则该种类型洪水巨灾债券的价格为

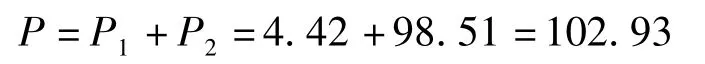
3.3洪水巨灾债券价格敏感性分析

(1)损失金额对债券价格的影响。在以上计算洪水巨灾债券价格时，我们发现在不同的损失程度下巨灾债券的价格也不尽相同，因此，本文基于表2中所给出数据分析不同损失程度对洪水巨灾债券价格的影响。在表2中我们可以得到各损失程度下的触发值以及相对应的概率情况，此处假定所有巨灾债券均为本金无保证型债券，且为便于比较，此处假定为单一时期债券。基于以上假定可以计算出各损失程度下的年收益率及债券价格，如表3所示。

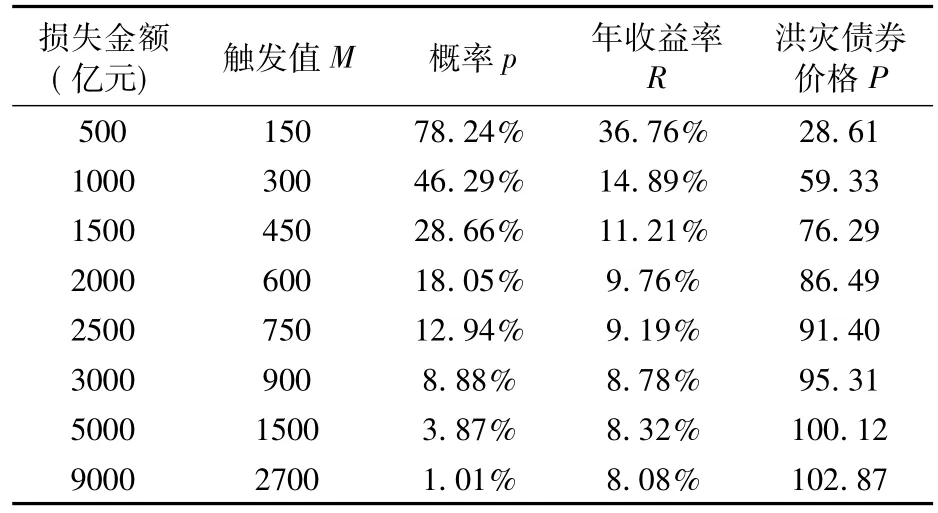
表3　不同损失金额下的洪灾债券价格

从表3中我们可以看出，随着损失程度的增大，实际巨灾损失突破触发值的概率p在减小，也就是说巨灾事件造成本金损失的可能性在逐渐降低，因此洪水巨灾债券的价格也就呈现上升趋势。

(2)本金收回比例对债券价格的影响。在以上计算洪水巨灾债券价格时，我们发现除不同损失程度会对债券价格造成影响外，不同的本金收回比例也会对债券价格造成影响。因此，我们可以选取某个固定损失程度点，并对此损失金额采取不同本金收回比例，最终计算出不同本金损失比例下的债券价格。在分析本金收回比例对巨灾债券价格的影响之前，我们做出如下假定:①选取损失金额为2000的点进行分析;②本金收回比例选取100%、80%、50%、20%、0%等5种比例进行比较;③洪水巨灾债券为单一时期巨灾债券;④由于是在同一损失程度下进行的分析，因此收益率应相差不大，故在此处假定各种本金收回比例的年收益率均以本金收回比例100%的收益率9.76%为准。

基于以上假定，我们可以计算出5种不同本金收回比例下洪水巨灾债券的价格，如表4所示。

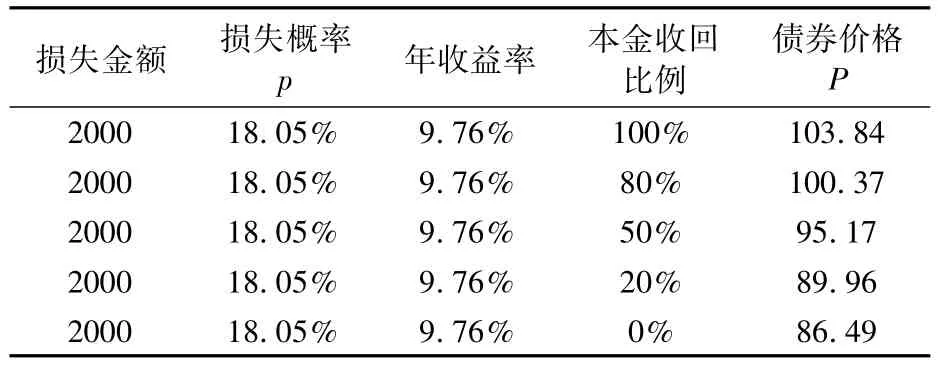
表4　不同本金收回比例所对应的洪灾债券价格

从表4的计算结果中我们可以看出，在损失金额保持不变，年收益率固定的情况下，随着本金收回比例的不断降低，债券价格也在不断降低。因为在其他情况维持不变的情况下，随着本金收回比例的不断地降低，投资者所承受的风险也在不断地增大，洪水巨灾债券价格在此种情况下也就出现了不断降低的趋势。

4　研究结论及政策建议

本文通过引入Monte Carlo模拟对洪灾损失数据进行分布拟合，以非寿险精算原理为基础，结合资本资产定价原理及相应巨灾债券定价原理，对我国洪水巨灾债券定价研究进行了初步探索，并得出以下结论及相应建议:

首先，在对本文所研究洪水巨灾债券进行价格敏感性分析后，我们发现随着损失程度的增加，洪水巨灾债券年收益率下降得很快，且债券价格不断上升。这种情况对于洪水巨灾债券的推行极为不利。例如，在损失程度较大的年份时，投资者需要付出较高的价格而获得的收益率却比较低，这将会大大打击投资者的积极性。因此，政府或推行巨灾债券的保险公司、再保险公司应采取相应策略以缩小不同损失程度间债券收益率及价格的差距，提高投资者积极性。

其次，在分析本金收回比例对洪水巨灾债券价格的影响时，可以看出本金完全收回与本金无收回的债券价格相差较大，这两种比例的设置都会影响债券发行人及投资者的行为。因此，需要从本金收回比例出发，根据证券市场的实际情况，制定一个合理的本金收回比例，使巨灾债券的供需双方都能最大程度地接受。这个比例不能太高也不能太低。

最后，在对我国洪水灾害损失数据进行收集时，我们发现我国现阶段的洪水灾害数据的搜集、处理等成本极高且现阶段的数据也存在较大的滞后性，使得在获取精确、真实的洪水灾害数据上难度增加。详实准确的巨灾损失数据是巨灾债券定价的重要依据，故目前亟需在我国建立相应的灾害数据统计数据库，从而保证巨灾风险研究所需数据的及时性、真实性和可靠性。

参考文献:

［1］Goshay R C，Sandor R.An inquiry into the feasibility of a reinsurance futures market［J］.Journal of Business Finance，1973，5(2):56-66.

［2］Kunreuther H，Pauly M.Neglecting disaster:why don’t people insure against large losses［J］.Journal of Risk and Uncertainty，2004，28(1):5-21.

［3］Froot K.The evolving market for catastrophic event risk ［J］.Risk Management and Insurance Review，1999，2 (3):1-28.

［4］Lane M N.Price，risk and ratings for insurance linked notes:evaluating their position in your portfolio［J］.Derivatives Quarterly，1998，4(4):36-52.

［5］Lin Y，Cox H.Securitization of catastrophe mortality risks［J］.Insurance:Mathematics and Economics，2008，42(2):628-637.

［6］Chang C W，Chang J S K，Lu W L.Pricing catastrophe options with stochastic claim arrival intensity in claim time［J］.Journal of Banking＆Finance，2010，34(1):24-32.

［7］施建祥，邬云玲.我国巨灾保险风险证券化研究——台风灾害债券的设计［J］.金融研究，2006，(5):103-112.

［8］田玲，张岳.巨灾风险债券定价研究的进展述评［J］.武汉大学学报(哲学社会科学版)，2008，61(5):650-654.

［9］庹国柱，赵乐，朱俊生.政策性农业保险巨灾风险管理研究［M］.北京:中国财政经济出版社，2010.61-63.

［10］韩天雄，陈建华.巨灾风险证券化产品的定价问题［J］.保险研究，2003，(12):31-33.

［11］Cox S，Pederson H.Catastrophe risk bonds［J］.North American Actuarial Journal，2000，4(4):56-62.

［12］田玲，向飞.基于风险定价框架的巨灾债券定价模型比较研究［J］.武汉大学学报(哲学社会科学版)，2006，59(2):168-174.

［13］Wang S.Cat bond pricing using probability transform ［A］.Special Issue on Insurance and the State of the Art in Cat Bond Pricing［C］.Geneva Papers:Studies and Folders Series(No.278)，2004.19-29.

［14］Christofides S.Pricing of catastrophe linked securities ［A］.ASTIN Colloquium International Actuarial Association［C］.Bergen，Norway，2004.1-28.

［15］施建祥，秦倩琪.基于极值理论的地震巨灾债券定价［J］.统计与决策，2008，(21):18-20.

［16］李永，范蓓.多事件触发巨灾债券设计与定价研究［J］.中国软科学，2012，(3):41-48.

［17］谢世清，梅云云.巨灾期权的保险精算定价探析［J］.现代财经:天津财经大学学报，2011，(8):101-107.

［18］韦勇凤，李勇，巴曙松.巨灾债券对投资组合分时期影响的实证分析［J］.保险研究，2012，(8):121-127.

［19］翁成峰，韦勇凤，巴曙松.中国参数化地震巨灾债券的定价分析［J］.中国科学技术大学学报，2013，43 (12):1026-1032.

［20］韦勇凤，翁成峰，李勇.基于Wang双因素变换的公私合作中国地震巨灾债券定价［J］.数理统计与管理，2015，34(3):513-520.

［21］田玲.巨灾风险债券运作模式与定价机理研究［M］.武汉:武汉大学出版社，2009.141-179.

Catastrophe Risk Bonds Pricing Based on Monte Carlo Simulation——Taking Flooding Catastrophe Bonds in China as an Example

HUANG Ying-jun，LI Jiang-yan，HAN Jing-wei
(School of Economics and Business Administration，Chongqing University，Chongqing 400030，China)

Abstract:Data in recent years consistently shows that China is one of the countries with most serious natural disasters by flood.Therefore，how to cover the flood loss effectively based on the precaution of the flood disaster becomes an issue concerned by the world.During the test of all kinds of catastrophe risk management tools，catastrophe risk bonds becomes one of the most effective tools of bridging the equity market and insurance market because of its low risk in investment and high return.This article aims to investigate to the feasibility of catastrophe risk bonds in China and make a preliminary investigation of the pricing of flood catastrophe risk bonds based on the non-life actuarial principles and the capital asset pricing model.

Key words:catastrophe bonds pricing; Monte Carlo simulation; flooding catastrophe bonds

基金项目:国家社会科学基金重点资助项目(10AGL010)

收稿日期:2015-05-07

中图分类号:F842.6

文献标识码:A

文章编号:1003-5192(2016)02-0050-06

doi:10.11847/fj.35.2.50