多模式资源受限项目调度问题的双目标优化
顾 坤, 徐 哲
(北京航空航天大学经济管理学院,北京 100191)
多模式资源受限项目调度问题的双目标优化
顾 坤, 徐 哲
(北京航空航天大学经济管理学院,北京 100191)
摘 要:除了追求项目工期最短,减少资源需求量波动也是项目管理者需要考虑的问题,但在实际项目执行时,追求较均衡的资源需求量则有可能导致项目延期,因此需要进行项目工期和资源均衡程度的权衡。综合考虑资源的多样性与活动的多执行模式,以项目工期和资源均衡为优化目标,建立多模式项目调度问题的双目标优化模型。提出一种基于非支配排序遗传算法的双目标混合遗传算法来求解问题的帕累托最优解,在算法中设计违背约束的惩罚方法和可行解的筛选过程。通过算例分析验证模型与算法的有效性,并分析网络参数和资源强度对帕累托解集的影响,说明求解帕累托解集的必要性,为项目管理者确定项目调度方案提供决策依据。
关键词:资源受限项目调度;多模式;双目标优化;资源均衡;遗传算法
本文信息:顾 坤,徐 哲.多模式资源受限项目调度问题的双目标优化[J].石家庄铁道大学学报:社会科学版,2016,10(1):6-14.
项目调度是在满足活动优先关系约束、资源约束及其它项目需求的基础上,为项目中的每个活动确定开始时间,形成基线进度计划,以满足项目的某些绩效指标(如最小化项目工期、均衡资源利用等)。经典的资源受限项目调度问题(Resource-Constrained Project Scheduling Problem,RCPSP)已经被证明是NP难问题,并得到了广泛深入的研究[1],其主要工作包括项目进度计划的制定和资源的安排[2],每个活动具有单一的工期和资源需求量。一般可以通过增加活动的资源使用量以缩短活动工期,从而形成不同的资源量与工期组合,这就产生了多模式资源受限项目调度问题(Multi-mode Resource-Constrained Project Scheduling Problem,MRCPSP)[3],其中活动的每种执行模式对应特定的工期和资源需求量组合。目前,MRCPSP研究的主要是在资源及优先关系约束下,求解得到每个活动的执行模式和开始时间以使得项目工期最短[4]。
项目管理者在优化项目工期的同时,尽量避免造成可更新资源(如人力、大型机器、设备等)的需求量出现“高峰”和“低谷”。因此,有时还会要求项目在满足活动优先关系和项目工期约束条件下,在一定时间内合理安排每个活动的开工时间,最小化资源使用量的变异,使资源高效均衡利用,即资源均衡问题(Resource Leveling Problem,RLP)。
在资源均衡问题中,多数研究假设不存在资源约束,文献[5]和文献[6]在不考虑资源约束及给定项目截止日期的情形下,最小化资源使用量与均值的方差;文献[5]采用整数线性规划求解RLP,但是求解时间较长;文献[6]借助非连续动态规划成功解决小规模RLP;文献[7]研究存在截止期限的多模式资源受限项目调度资源均衡问题,提出一种基于分支定价的启发式算法;文献[8]提出了一个基于时间窗的分支定界算法,该算法的核心思想是巧妙枚举活动的可行开始时间;与文献[8]不同,文献[9]的分支定界算法是建立在枚举准稳进度计划的基础上。针对大规模问题,许多研究开始聚焦于启发式算法,文献[10]提出了一个基于优先权的启发式算法和一个禁忌搜索算法;文献[11]设计了基于种群的迭代贪婪搜索算法,并通过计算实验证明其算法可以有效求解含有多达1000个活动的项目资源均衡问题;文献[12]研究了通过活动分裂来实现资源均衡,并实现了一个求解资源均衡问题的遗传算法。
此外,在多目标优化研究中,资源均衡也是优化的目标之一。文献[13]研究了资源受限情况下资源均衡和净现值双目标优化问题,设计分支定界算法对多种资源进行优化;文献[14]中,定义成本由活动不同模式产生的直接成本和与项目工期有关的间接成本两部分组成,继而研究了多模式资源受限下的离散时间/成本权衡问题(Multimode Resource Constrained Discrete Time/Cost Trade-off Problem,MRC-DTCTP),设计了遗传算法对问题进行求解;文献[15]在可更新资源和活动优先关系约束下研究了MRC-DTCTP,同时对项目工期、成本及资源均衡三个目标进行优化;文献[16]和[17]都研究了模糊多目标“时间-成本-资源”优化问题,优化了时间、成本和资源均衡三个目标,使用模糊集理论对不确定的活动工期参数建模,分别采用NSGA-II算法和混合遗传-粒子群算法来获取基线进度计划。
基于上述分析可以看出,对多模式资源受限项目调度问题的RLP研究较少,已有研究主要以可更新资源不受限或受限为基础,较少考虑不可更新资源约束。成本作为一种特殊的不可更新资源,在实际项目开始之前,管理者往往对成本有大概的估计,即项目预算,因此需对项目成本进行单独考虑。本文在综合考虑可更新资源,不可更新资源以及总成本约束的条件下对多模式项目调度问题进行研究,同时优化项目工期和资源均衡水平。首先对所研究的问题进行数学描述,建立成本约束下的多模式资源受限项目调度问题的双目标优化模型,然后,设计改进的双目标混合遗传算法并对算例进行求解,验证模型与算法的有效性,最后通过算例实验,给出深入的计算实验分析与结果。
一、问题描述
本文采用节点式(activity-on-node,AON)项目网络图,活动有多种执行模式,不同模式对应不同的工期、成本及资源需求量组合,具体参数描述如表1。项目决策者综合权衡项目工期和资源均衡程度,在满足优先关系、可更新资源、不可更新资源及成本约束的条件下,以项目工期和资源正向偏差的最小化为目标,为每个活动选择一个执行模式,安排各活动的开始时间,即求解多模式资源受限项目调度问题的帕累托最优集。
二、数学模型
本文所研究的调度问题有两个优化目标:第一个目标是最小化项目工期,即最后一个活动的完工时间;第二个目标是可更新资源的均衡水平,该指标采用可更新资源每个时段的实际使用量与均值的正向偏差的加权和进行衡量,该目标值越小越好。例如,人力资源作为典型的可更新资源,项目管理者在规划时应避免加班情况出现,而适当的闲暇相对可以接受,所以目标函数采用对正的偏差进行惩罚,更符合实际。
建立的项目调度模型如下:
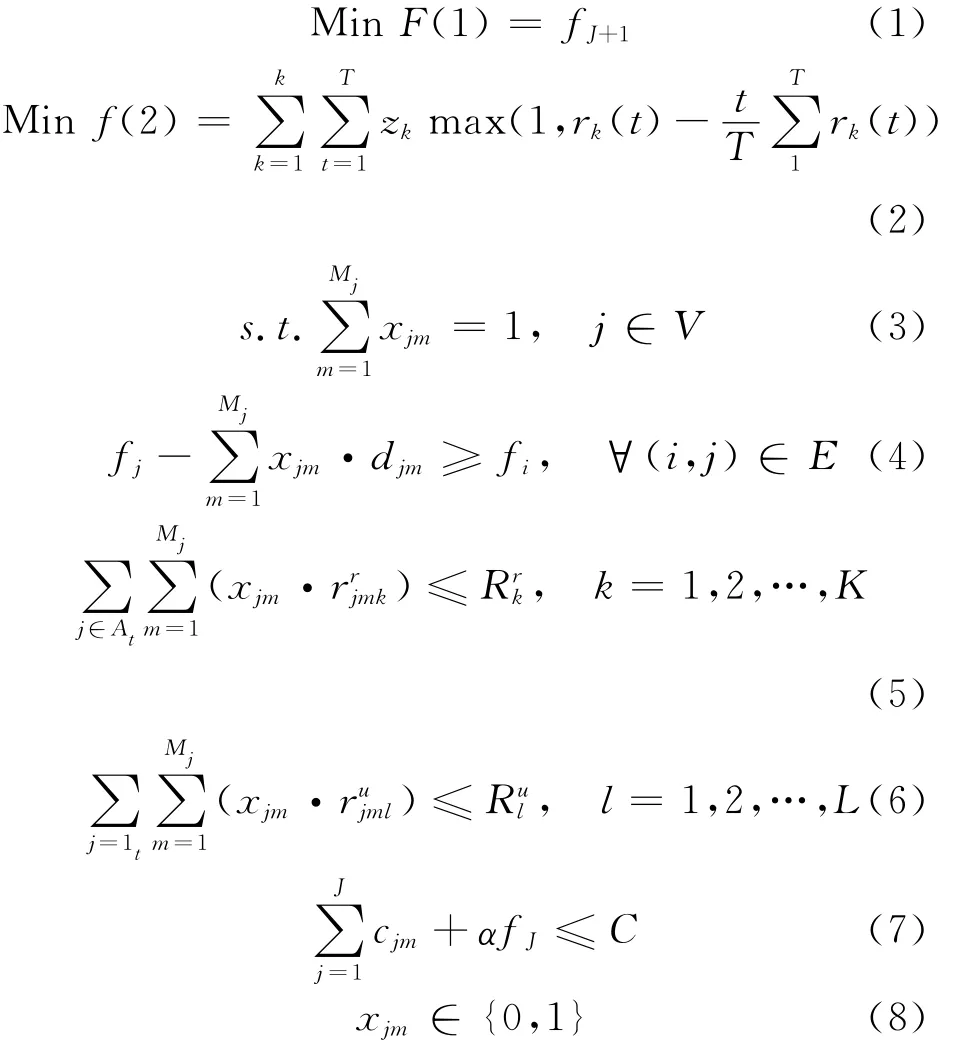
式(1)表示最小化项目工期;式(2)表示资源均衡的目标函数,rk(t)是可更新资源k在时段的实际使用量;式(3)确保了每个活动在执行时只能采用一种执行模式;式(4)表示活动间的优先关系约束;式(5)意味着每种可更新资源在每个时段的需求量不能超过其可用量,其中At代表时段内正在进行的活动集合;式(6)表示不可更新资源的可用量有限;式(7)是项目成本约束;式(8)为活动模式选择变量,活动j以模式m执行,则xjm=1,否则xjm=0。
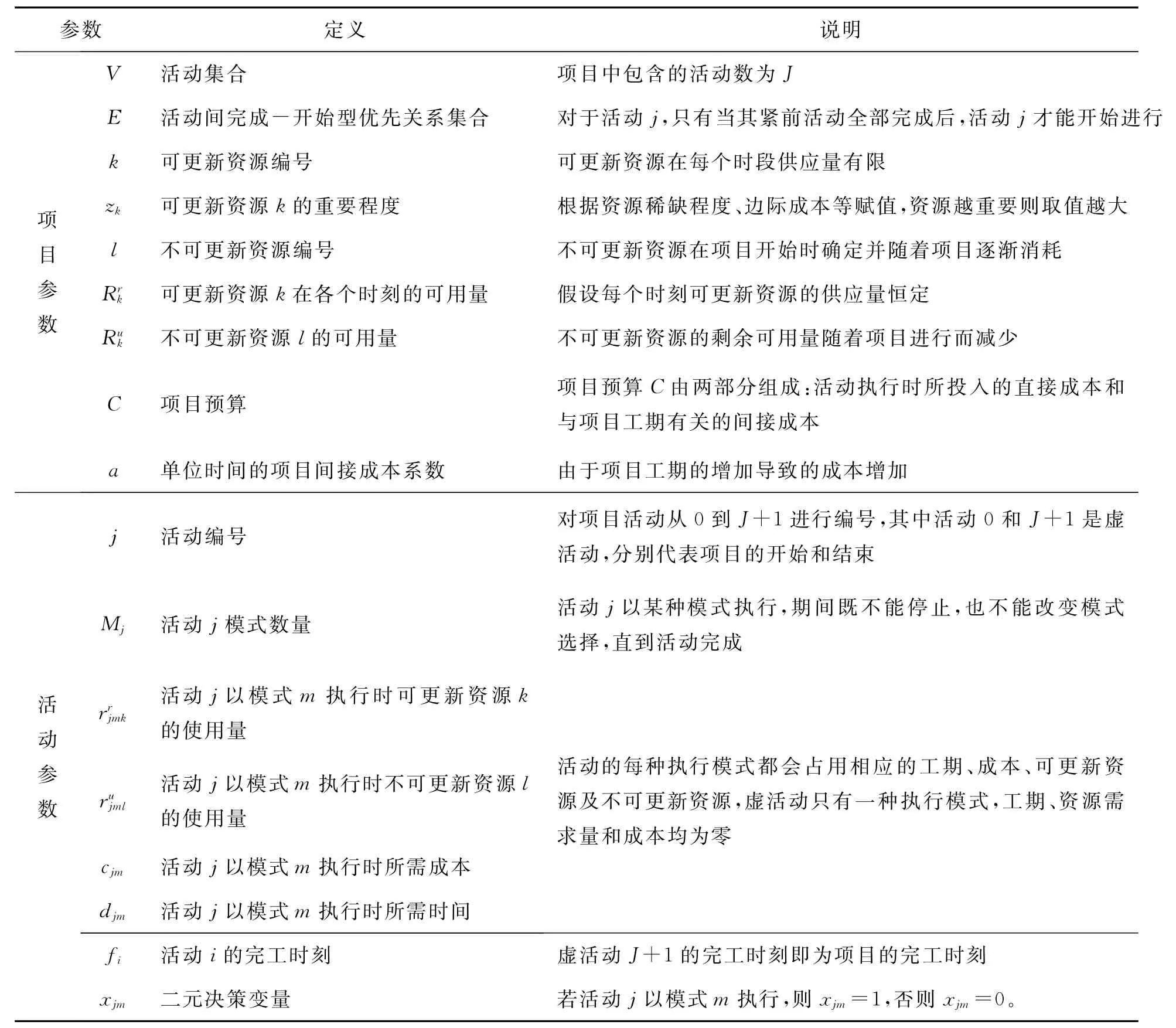
表1 参数定义及说明
三、双目标混合遗传算法
本文研究多模式资源受限项目调度的双目标优化问题,采用非支配排序遗传算法NSGA-Ⅱ对上述模型进行求解。
本文设计的算法框架如图1所示,首先,随机产生可行解作为初始种群以保证初始解的优良性,然后,在确定了各种资源及成本的可用量条件下,对初始种群执行遗传操作和非支配排序直到达到最大进化代数;最后,对所得解集进行筛选。
(一)解的编码及解码方式
在算法中,由满足紧前关系的活动列表链和模式列表链相结合的方式对染色体进行编码,活动列表链和模式列表链一一对应,如图2,项目网络中有6个活动,第一行表示染色体的活动执行顺序,第二行为各活动对应的执行模式。依据串行调度生成机制对各个染色体进行解码,在同时满足可更新资源约束和紧前关系约束的条件下,确定各个活动的最早开工时间,生成可行的调度计划,从而得到染色体所对应的两个适应值:项目工期和可更新资源使用量正向偏差加权和。
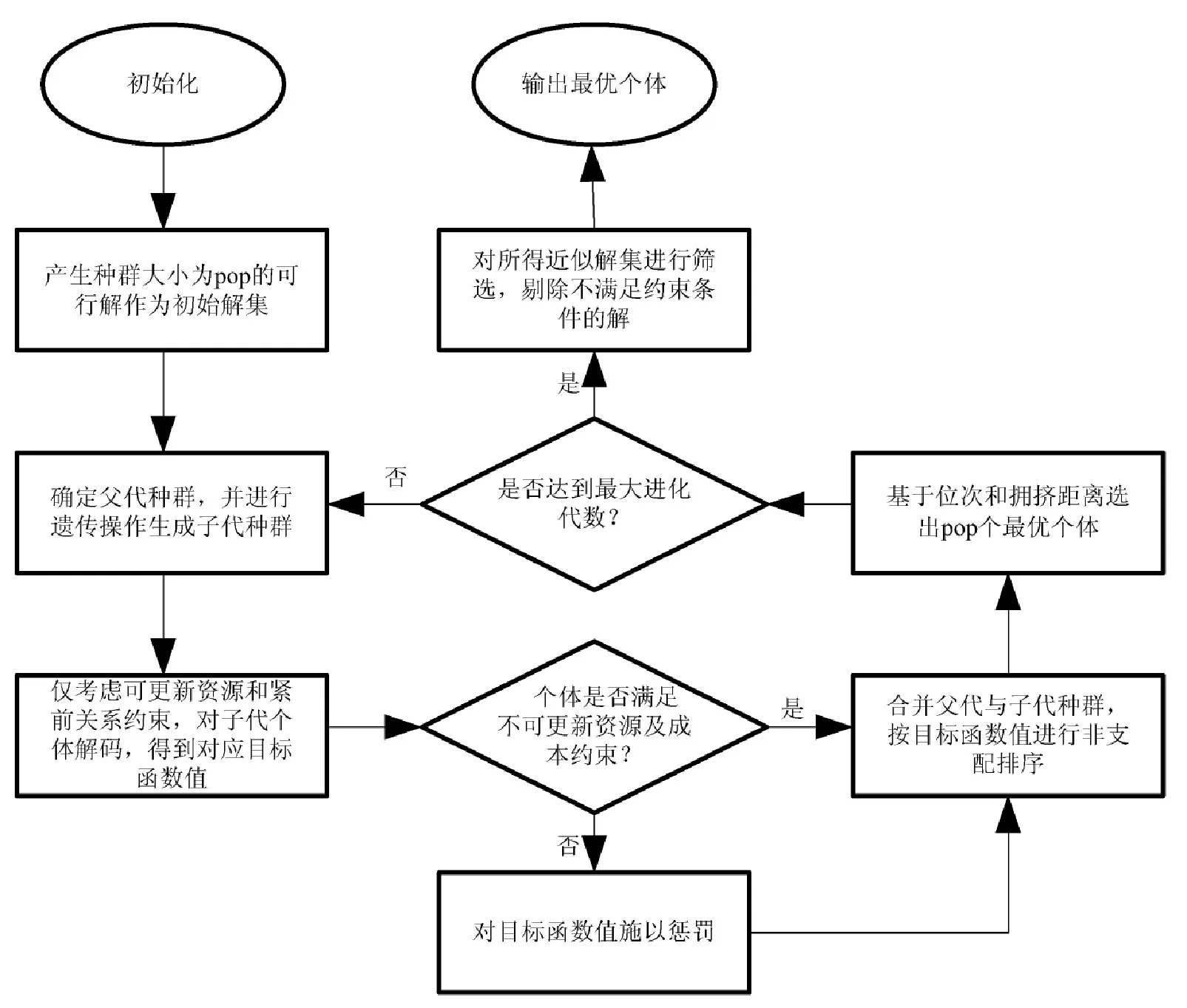
图1 双目标混合遗传算法流程图
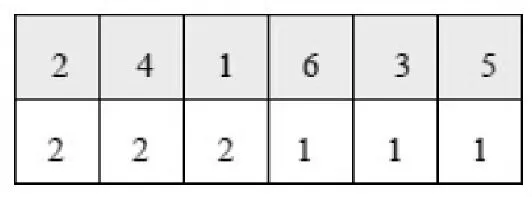
图2 双链染色体结构示意图
(二)初始种群
随机抽取满足紧前关系约束的活动列表和模式列表组成个体,计算其不可更新资源使用量及成本,如果满足约束,则将该个体放入初始种群,直至初始种群规模达到pop。
(三)遗传算子
1.选择算子
通过非支配排序,得到各个染色体的位次和拥挤距离,根据偏序关系定义对种群进行选择操作,即如果两个个体的非支配排序不同,取位次较小的个体;如果两个个体在同一级,取周围较不拥挤的个体。
对于每个个体p都设有以下两个参数np和sp。其中np为在种群中支配个体p的个体的数量,sp为被个体p所支配的解个体的集合。据此对种群中的个体进行非支配排序,从而将种群划分为N个互不相交的非支配边界集{F1,F2,…,FN}。若p∈Fa,则个体p的位次为a;对同一个位次的个体按目标函数进行升序排列,计算p的拥挤距离,有
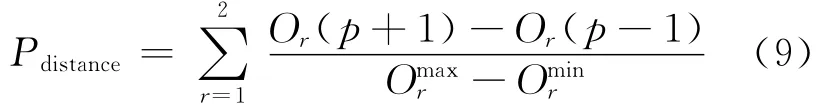
式中,Or(p+1)和Or(p-1)分别为与p的目标函数值相邻的两个个体所对应的目标函数值,Omaxr和Ominr分别为属于Fa的所有个体的第r个目标函数的最大值和最小值。
每次遗传迭代后,将子代种群与父代合并,新种群大小为2pop,按上述方法选取靠前的pop个个体。
2.交叉和变异
在遗传操作中,亲代染色体都有一定概率发生交叉,交叉由两条链分别进行,其中活动列表链采取两点交叉,模式列表链采取单点交叉。
子代个体以一定概率发生变异,对于活动列表的变异,在满足优先关系的前提下,交换选定活动j和活动j+1的位置;对于模式列表的变异,随机选定一个活动,将其执行模式随机改变。
(四)目标函数值的惩罚
通过遗传操作之后,需要对子代种群的可行性进行判断,如果子代个体超出了不可更新资源约束或成本上界,则应减少其进入下一代遗传的概率。设F(1)j、F(2)j分别为个体j解码后得到的两个目标函数值,选取惩罚函数为
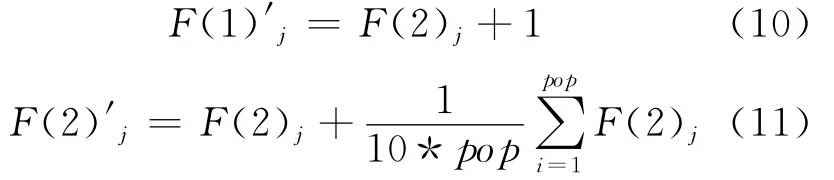
式中,F(1)′j为惩罚后的工期值,F(2)′j是对资源均衡函数进行惩罚所得值,即在个体j已有均衡函数值的基础上增加该代种群均衡函数均值的十分之一。
(五)最终解的筛选
当种群进化到最大代数后,遗传操作停止,对所得近似解集进行筛选,剔除违背不可更新资源和成本约束的不可行解,得到最终可行解。
四、算法测试
本文实例根据文献[14]进行改编,项目网络图如图3所示,项目中共包含8个活动,其中活动0和活动7是虚活动,表示项目的开始和结束;活动1至6为实活动,每个活动有2种模式,各模式由活动工期、可更新资源需求量、不可更新资源需求量以及活动的直接成本组成。假设项目的执行只需要一种可更新资源以及一种不可更新资源,可更新资源可用量Rr=6,不可更新资源可用量Ru=15,项目预算C=215,单位时间的间接成本a=1。
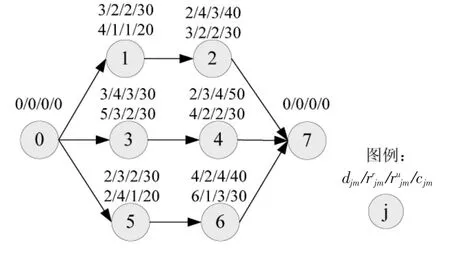
图3 示例项目的AON网络图
采用Matlab实现本文的双目标混合遗传算法。设置参数如下:种群规模pop=200,最大进化代数分别为1、5、10、100,染色体交叉概率0.9,活动列表和模式列表的变异概率均为0.1。
取算法结束时所得100代的2个解作为帕累托最优解,以此作为比较基准,所对应的目标函数值向量分别为[8,2.625]和[9,1.556]。从多样性看,如图4所示,当进化代数为1时,得到2个近似解,所对应的目标函数值向量集合为{[9,2]和[11,1.828]}。当进化代数为5时,得到2个近似解,所对应的目标函数值向量集合为{[8,2.625]和[9,1.778]},其中包括一个帕累托最优解。从收敛性看,当进化代数为10时,得到全部帕累托最优解集,从第10代至算法结束,最优解集保持稳定。各代对应近似解的调度计划见图5。
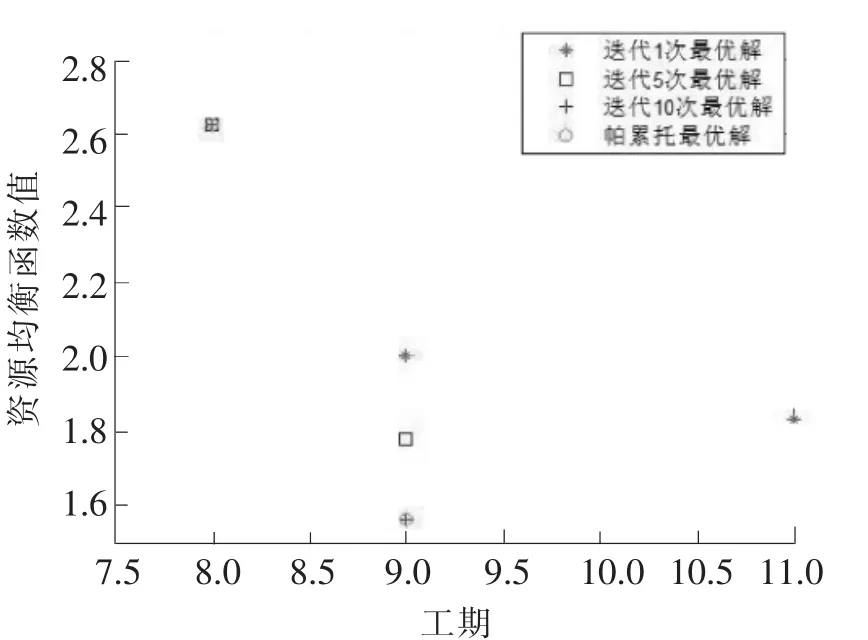
图4 种群进化所得解集与帕累托最优集的比较
从计算结果上看,与单目标MRCPSP模型相比,多目标问题会获得多个帕累托最优解,为项目管理者提供了更多决策空间,并且,每个最优解对应多个调度方案,体现了解的差异性和多样性。按文献[2]的模型和算法,仅以工期最短为目标对本算例求解,得到最优项目工期为8。但是,在实际项目管理中,如果项目更偏向于对资源的均衡利用,管理者也可能会采用工期较长、资源更均衡的调度方案。
五、实验分析
本节通过对随机生成的算例集合进行分析,验证算法的有效性。由项目调度问题算例生成器Progen2.0软件生成具有不同结构的活动网络,通过对每个算例的参数进行定义生成本文所需要的算例集合。采用资源强度(RS)测度资源稀缺程度,RS越小,表示资源越稀缺;采用网络复杂度(NC)测度活动网络的复杂程度,NC越大,表示活动间约束越多。实验参数设置见表2,指定活动个数N取3个不同的值,NC取2个不同的值,RS取4个不同的值,每种参数组合随机产生10个算例,从而得到个算例。算法通过Matlab编程实现,实验参数设置如下:最大进化代数设为50代;种群个数为40;交叉概率为0.8,变异概率为0.1。
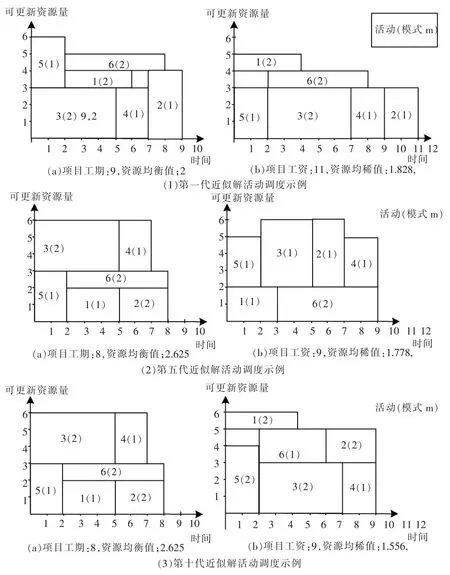
图5 各代对应最优解的活动调度示例
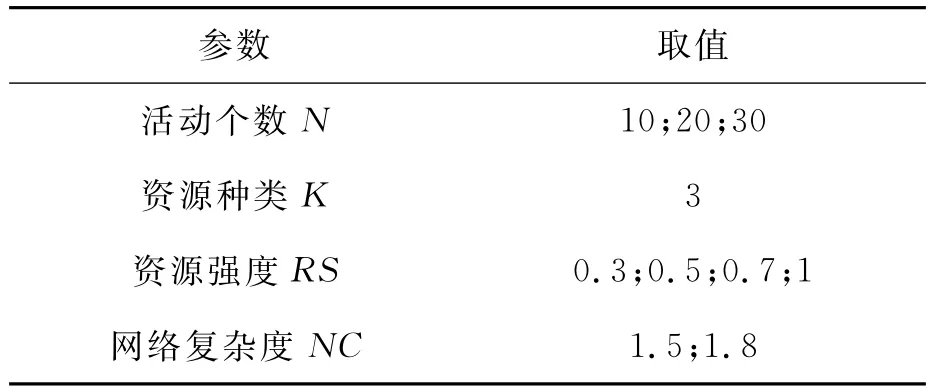
表2 实验参数设置
(一)考察网络参数、资源强度对帕累托解个数的影响
对240个算例进行求解,根据活动个数N的取值进行统计归类,计算帕累托解个数的均值,绘制图6。考察图6,可以得出以下结论:①当N增大时,解的个数随之增大,说明活动数多的项目调度问题具有更多的帕累托解;②NC从1.5到1.8变化时,解的个数略有减少,这说明对于网络复杂度低的项目,帕累托解的数量会越多;③当RS变化时,解的个数变化没有明显的规律性,这是因为,随着资源强度的RS增大,项目工期会缩短,由此产生新的解,但是,如果新解的资源均衡指标值优于之前的解,则将淘汰一个或多个已有解,因此,解的个数没有一致的变动趋势。
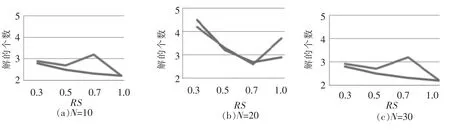
图6 不同参数下所得帕累托解个数的均值
(二)考察资源强度对帕累托解集的影响
在上节中讨论了网络参数对帕累托解数量的影响,发现网络活动数量(N)越多,网络复杂度(NC)越低的项目,帕累托解的数量会越多,因此本部分选取N=30、NC=1.5的情形考察资源强度RS对帕累托解集的影响。图7和图8均给出了算例实验中NC=1.5、N=30组的帕累托解集随RS变化的散点图。考察图7可以看出,当资源强度(RS)增大时,优化目标值更优,这说明资源供应越充足,可以同时获得工期短,资源均衡水平高的调度计划,有效地实现了优化调度的目的。考察图8可以看出,资源强度(RS)依次取1、0.7、0.5、0.3时,帕累托解集逐步向外围移动,且移动幅度有扩大的趋势。即当资源供应充足时,RS的适度减少(RS值从1减小到0.7),对优化结果的影响较小;而当资源供应紧张时,此时减小RS (RS值从0.5减小到0.3)会使工期和资源均衡度水平明显变差。
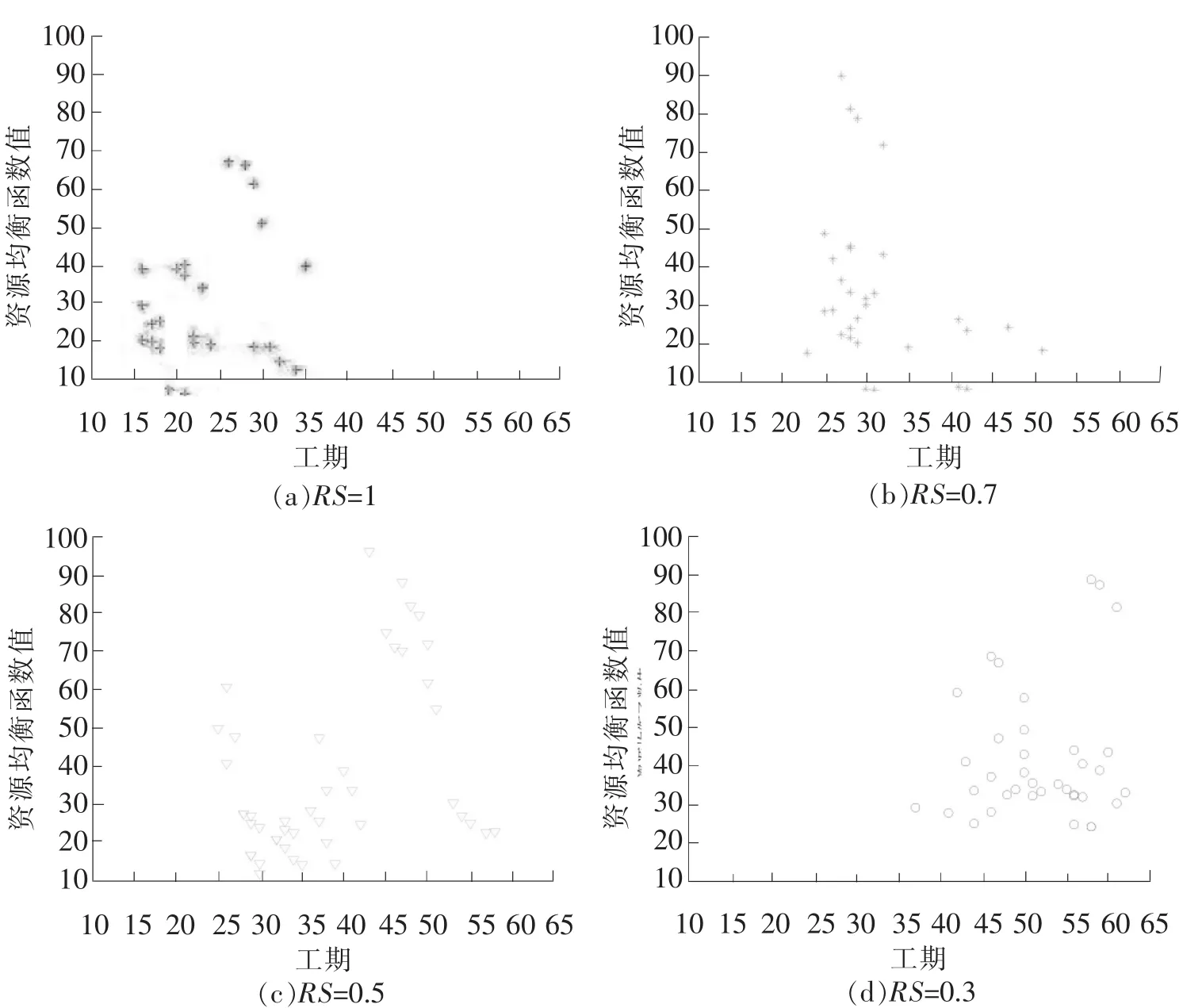
图7 NC=1.5、N=30时优化结果随RS变化散点图
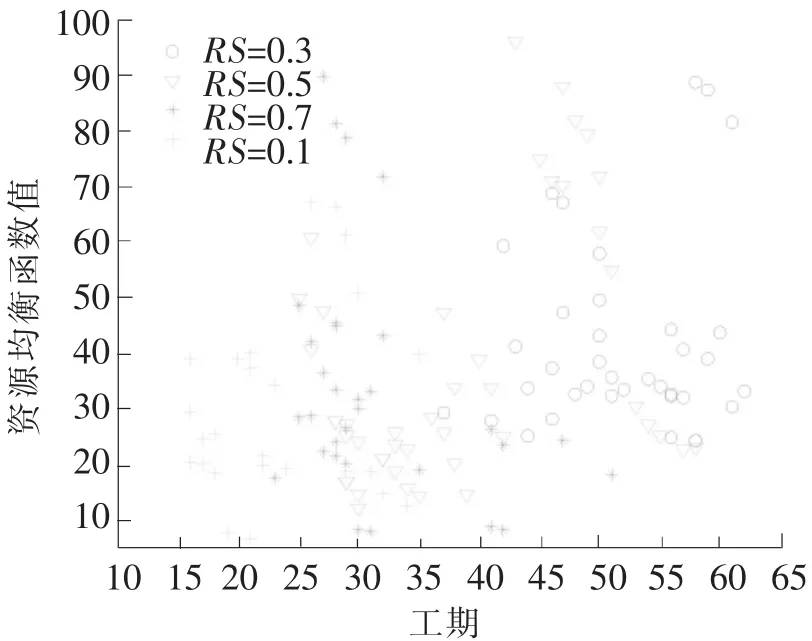
图8 NC=1.5、N=30时,优化结果随RS变化散点图
六、结论
综合考虑资源的多样性与活动的多执行模式,同时优化项目工期和资源均衡水平,建立了多模式项目调度问题的双目标优化模型。设计了一种基于非支配排序遗传算法的双目标混合遗传算法求解帕累托最优解,通过算例分析验证模型与算法的有效性,并测试分析了网络参数及资源强度对帕累托解集的影响。研究发现,活动数量多、网络复杂度较低的项目可以获得更多的帕累托解,即项目决策者有更大的选择空间;当资源供应充足时,可以同时获得工期短,资源均衡水平高的调度计划,有效实现优化调度的目的,而当资源供应紧张时,工期和资源均衡水平的优化结果会明显变差。
参考文献:
[1]李明.项目人力资源调度研究综述[J].石家庄铁道大学学报:社会科学版,2015,9(1):54-60.
[2]顼志芬,王春想.基于项目组合管理理论的研发项目管理流程研究[J].石家庄铁道大学学报:社会科学版,2013,7(1):1-4.
[3]Mori M,Tseng C C.A genetic algorithm for multimode resource constrained project scheduling problem [J].European Journal of Operational Research,1997,100(1):134-141.
[4]Sprecher A,Hartmann S,Drexl A.An exact algorithm for project scheduling with multiple modes[J].OR Spektrum,1997,19(3):195-203.
[5]K.A H,E.B J.Integrated project task and manpower scheduling[J].IIE Transactions.1997,29(9):711-717.
[6]Coughlan E T,Lübbecke M E,Schulz J.A branchand-price algorithm for multi-mode resource leveling [M].Experimental Algorithms.Springer Berlin Heidelberg,2010:226-238.
[7]Neumann K,Zimmermann J.Procedures for resource leveling and net present value problems in project scheduling with general temporal and resource constraints[J].European Journal of Operational Research,2000,127(2):425-443.
[8]Gather T,Zimmermann J,Bartels J H.Exact methods for the resource leveling problem[J].Journal of Scheduling,2011,14(6):557-569.
[9]Neumann K,Zimmermann J.Resource levelling for projects with schedule-dependent time windows[J].European Journal of Operational Research,1999,117 (3):591-605.
[10]Ballestín F.When it is worthwhile to work with the stochastic RCPSP[J].Journal of Scheduling,2007,10(3):153-166.
[11]Hossein Hashemi Doulabi S,Seifi A,Shariat S Y.Efficient hybrid genetic algorithm for resource leveling via activity splitting[J].Journal of Construction Engineering and Management,2010,137(2):137-146.
[12]Neumann K,Zimmermann J.Procedures for resource leveling and net present value problems in project scheduling with general temporal and resource constraints[J].European Journal of Operational Research,2000,127(2):425-443.
[13]Peng W L,Wang C G.A multi-mode resource-constrained discrete time-cost tradeoff problem and its genetic algorithm based solution[J].International Journal of Project Management,2009,27(6):600-609.
[14]Ghoddousi P,Eshtehardian E,Jooybanpour S,et al.Multi-mode resource-constrained discrete time-costresource optimization in project scheduling using nondominated sorting genetic algorithm[J].Automation in construction,2013,30:216-227.
[15]Zahraie B,Tavakolan M.Stochastic time-cost-resource utilization optimization using non-dominated sorting genetic algorithm and discrete fuzzy sets[J].Journal of Construction Engineering and Manage-ment,2009,135(11):1162-1171.
[16]Ashuri B,Tavakolan M.Fuzzy enabled hybrid genetic algorithm–particle swarm optimization approach to solve TCRO problems in construction project planning[J].Journal of Construction Engineering and Management,2011,138(9):1065-1074.
[17]Drezet L E,Billaut J C.A project scheduling problem with labor constraints and time-dependent activities requirements[J].International Journal of Production Economics.2008,112(1):217-225.
Bi-objective Optimization for the Multi-mode Resource-constrained Project Scheduling Problem
GU Kun,XU Zhe
(School of Economics and Management,Beihang University,Beijing,100191,China)
Abstract:In addition to the pursuit of the shortest project duration,reducing the fluctuation of resources demand is the problem mostly needed to be considered by project managers as well.During the actual implement of the project,the arrangement of a relatively balanced resources demand will probably lead to the delay of projects,thus the duration of project and the equilibrium level of resources need to be balanced.Concerning the diversity of resources and the verified execution mode of activities,aiming at the optimization of project duration and resource leveling,an optimized model of multimode project scheduling problem should be established.A double objective hybrid genetic algorithm is proposed based on the non-dominated sorting genetic algorithm to get the Pareto optimal solution of the problem.In the algorithm,the methods of punishment for violating the constraints and the filtering of feasible solution will be designed.The validity of the mode and algorithm will be testified by case operators,and case test will be carried out to analyze the influence of network parameters and resource intensity on Pareto solution sets,thus the necessity of solving the Pareto solution sets will be explained,which will provide the decision making basis for the project managers to determine the scheduling program for project.
Key words:resource-constrained project scheduling,multi-mode,bi-objective optimization,resources leveling,genetic algorithms
基金项目:国家自然科学基金(71271019,71571005);河北省社会科学基金(HB14GL023);河北省高等学校科学技术研究项目(QN2014035)。
作者简介:顾 坤(1990-),男,硕士研究生,研究方向:项目管理与调度。
收稿日期:2015-11-09
文章编号:2095-0365(2016)01-0006-09
中图分类号:N945
文献标识码:A
DOI:10.13319/j.cnki.sjztddxxbskb.2016.01.02

