三目标自适应变异微粒群算法的无功优化

马立新,王继银,栾　健,黄阳龙

(上海理工大学 光电信息与计算机工程学院,上海　200093)



三目标自适应变异微粒群算法的无功优化

马立新1,王继银2,栾健3,黄阳龙4

(上海理工大学 光电信息与计算机工程学院,上海200093)

摘要电力系统无功优化是提高电能质量保证电网运行的重要环节,文中建立了综合考虑有功网损和电压偏移最小及电压稳定裕度最大的三目标无功优化模型,引入了自适应变异微粒群算法用于解决三目标电力系统无功优化问题。该算法利用群体的适应度方差来动态监控微粒群聚集的状况,采用增加随机扰动的方法对聚集的微粒进行变异,并对惯性权重进行自适应调整,使该算法既能跳出局部最优,防止早熟,又能提高收敛速度和精度。将该算法与其他算法应用于IEEE-14节点系统中进行无功优化,通过数据的计算和比较,结果验证了该模型和算法用于解决多目标电力系统无功优化问题的优越性和实用性。

关键词微粒群算法;变异;三目标;无功优化;方差

无功优化(Reactive Power Optimization,RPO)是在各种约束条件下,通过调整发电机端电压、可调变压器变比、电容器补偿容量等控制变量来使电力系统的无功分布达到最优,从而保证电力系统的高效稳定运行。本文在传统的无功优化模型基础上,引入静态电压稳定裕度,建立了以节点电压偏移最小,有功网损最少以及电压稳定裕度最大为目标的优化模型。

微粒群算法(Particle Swarm Optimization,PSO)是一种群智能优化算法[1]。该算法参数简单,收敛速度快,作为寻优的一种工具,为众多学者所熟悉。但标准PSO算法存在着容易陷入局部极值,出现早熟等不足[2]。

基于标准PSO的上述不足,本文引入了一种自适应变异微粒群算法(Adaptive Mutation Particle Swarm Optimization,AMPSO)[3],并将其首次应用于三目标电力系统无功优化问题。该算法根据动态监控微粒群的聚集状况,增加随机扰动,对聚集的微粒进行变异,并自适应调整惯性权重,使该算法既能逃离局部极值防止早熟,又能提高收敛速度和精度。通过对IEEE-14节点系统的仿真计算,并与标准PSO及差分进化算法(Differential Evolution,DE)进行比较,验证了本算法解决RPO问题的可行性及优越性。

1三目标无功优化模型

1.1目标函数

本文以电压偏移和有功网损最小及电压稳定裕度最大为目标,建立优化模型。其中

(1)有功网损Ploss(经济性)

(1)

式中,N为系统网络总支路数;δi,δj是节点i和j的电压相角;Gk(i,j)为支路k的电导;Vi,Vj是节点i、j的电压。

(2)电压偏移dv(安全性)

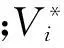
(3)静态电压稳定裕度(稳定性)

maxf3=VSM=λmin

(3)

式中,λmin是雅克比矩阵的最小特征值。

1.2约束条件

(1)功率约束。保持功率平衡

(4)

式中,Pi为有功功率;Qi为无功功率。

(2)变量约束。控制变量

(5)

式中,VG为发电机的端电压;T为可调变压器的变比;QC为补偿电容发出功率。

状态变量

(6)

式中,VL为负荷节点电压;QG为发电机无功出力。

1.3归一化处理

考虑到各目标函数量纲不同,不能进行统一加权,故作如下归一化处理

(7)式中,Ploss0,dv0分别为有功网损和电压偏移的初始值;Plossmin,dvmin分别为进行单目标优化时得到的最优值;VSM本身无量纲,为使所求各目函数有统一的最小值形式,故取倒数。归一化得到的总的目标函数为

minF=w1×Ploss′+w2×dv′+w3×VSM′

(8)

式中,w1,w2,w3分别为各目标函数的权值,且w1+w2+w3=1。

2微粒群算法

2.1标准微粒群算法

微粒群优化算法(PSO)是一种根据鸟群觅食行为,Kennedy和Eberhart提出的一种智能优化算法[4],参数较少,易于实现。PSO算法中每个微粒的速度和位置根据个体的历史最好位置和群体最好位置进行更新。式如下

vij(k+1)=wvij(k)+c1r1(pbestij(k)-xij(k))+c2r2(gbestj(k)-xij(k))

(9)

xij(k+1)=xij(k)+vij(k+1)

(10)

式中,vij(k)和xij(k)分别为为微粒i在第k次迭代中速度和位置的第j维分量;ω为惯性权重;c1、c2为学习因子;pbestij(k)为微粒i个体极值点位置的第j维分量;gbestj(k)为微粒群体全局极值点位置的第j维分量;r1、r2为[0,1]之间的随机数。

2.2自适应变异微粒群算法

由式(9)可看出,当群体全局极值点位置gbest长时间不变,微粒在搜索过程中会逐渐接近gbest,此时微粒速度的更新主要由个体极值点的位置pbest决定,其速度会逐渐减小,则整体微粒群会呈现一种趋同性,这种趋同性会导致微粒出现“聚集”现象,若此处为一局部最优,则该算法就会出现早熟现象。若在算法早熟时,通过改变微粒的全局极值,则微粒的速度就会发生变化,向其他方向进行搜索,从而跳出局部最优,进而找到全局最优值。鉴于此,本文通过分析微粒的聚集程度,来对微粒进行变异操作。

设fi为微粒i的适应度值,则由式(11)可得出n个微粒的平均适应度值。根据式(12)确定微粒群的归一化定标因子f,按照式(13)得出整个微粒群体的适应度方差σ2。

(11)

(12)

(13)

式(12)表明,微粒群群体适应度方差反映了微粒群的收敛程度,σ2越小,则群体越接近于收敛,相反,微粒群体处于随机搜索状态。

为使算法在出现早熟时,微粒向其他空间搜索,根据群体的适应度方差来确定群体全局极值变异的概率Pk,按下式[3]计算

(14)

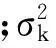
对于全局极值,采用增加随机扰动的方法[5]对其变异

gbestj(k)=gbestj(k)(1+η)

(15)

η是服从Gauss(0,1)分布的随机变量。

2.3调整学习因子和惯性权重

使学习因子能够异步时变[6],如式(16)所示

(16)

式中,c1f,c1i,c2f,c2i均为常数,本文取c1f=0.5,c1i=2.5,c2f=2.5,c2i=0.5;t为当前迭代次数;tmax为最大迭代次数。

采用式(17)进行惯性权重ω的调节

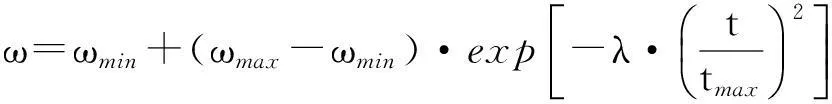
(17)

式中,λ为控制因子,ωmax和ωmin分别为惯性权重的最大值和最小值。

2.4无功优化步骤

步骤1导入算法的基本参数包括种群规模,最大迭代次数,微粒变异概率的最大值,最小值等,以及对应电力系统中的潮流数据。

步骤2对每一个微粒进行初始化,包括每一个微粒的初始位置,速度,初始个体极值和全局极值。

步骤3按式(16)～式(17)对学习因子,惯性权重自适应更新;按式(9)～式(10)对微粒速度,位置进行更新。

步骤4计算各微粒的适应度值并更新微粒个体、全局极值。

步骤5根据式(11)～式(13)分别计算微粒的平均适应度值、定标因子、适应度方差。

步骤6根据式(14)计算变异的概率Pk,随机产生数r∈[0,1],若r

步骤7更新微粒群体全局极值。

步骤8判断是否满足算法终止的条件,若符合则停止运行,输出最终的全局最优值,否则跳转步骤3继续执行。

3算例及结果分析

3.1测试数据

以IEEE-14节点系统为例进行测试分析,具体变量设置如下:节点1设置为平衡节点,节点2,3,6,8设置为PV节点,节点9为电容补偿节点,其余的节点均为PQ节点。支路5-6,4-7,4-9为变压器支路[7]。发电机的端电压在[0.95,1.10]之间变化(标幺值,该系统的基准容量为100MVA,下同);变压器变比调节区间为[0.90,1.10],调节步长为0.012 5;电容器可调节区间为[0.00,0.50],调节步长为0.05,Pmax=0.5,Pmin=0。该系统在优化前各优化目标的值分别为0.133 8、2.945 0、0.518 0[8-9]。

3.2优化结果分析

表1为本算法与其他算法得出的数据比较。表1中有功网损、电压偏移数值由图1和图2中最终收敛值反代入式(7)所得。由表1可知,三目标优化后效果均比优化前有明显提高,AMPSO算法在有功网损上比DE、PSO算法分别减少了0.71%和0.58%,比优化前减少8.3%;电压偏移,电压稳定裕度的优化效果也明显优于另外两种算法。

表1　IEEE-14节点系统各算法比较

由图1可知,AMPSO算法在优化有功网损过程中,在迭代次数接近20代时,就逐渐趋于稳定,接近80代则完全稳定,而其他两种算法均是80代后才稳定,可见AMPSO算法优化过程中收敛速度较快,且有功网损数值明显小于另外两种算法,而有功损耗越小,则表明经济性越好。

图1　IEEE-14节点系统有功损耗

由图2可知,AMPSO算法在优化电压偏移过程中,最终优化值虽然与另外两种算法较接近,但一开始收敛速度就较快,明显快于另外两种算法,且最终优化值也小于DE和PSO算法。可见该算法的优势还是可观的,而电压偏移越小,则表明电网的安全性越高。

图2　IEEE-14节点系统电压偏差

由图3可知,AMPSO算法在优化电压稳定裕度过程中,相比另外两种算法,在收敛速度上明显较快,且该算法电压稳定裕度较大,而裕度越大,则更有利于电网的稳定性。

图3　IEEE-14节点系统电压稳定裕度

各算法优化后的负荷节点电压的分布图如图4所示。

图4　优化后各节点电压分布

由图4可看出,AMPSO算法优化后各节点电压幅值均无越限,相比DE和PSO算法,各节点电压值更接近额定值,波动较小,优化后对电压有较大的改善。

综合以上可知,AMPSO算法在同时对3个目标进行无功优化过程中,三目标均有了较大改善,且相比其他算法,无论在速度上还是最终优化值上都较优,可见该算法不仅提高了解的质量和精度,也加快了收敛的速度,故可更好地解决无功优化问题。

4结束语

本文建立了三目标优化模型,采用自适应变异的方式对微粒进行改善,克服了标准微粒群算法易陷入局部最优,出现早熟的不足,对惯性权重和学习因子进行自适应调整,提高了算法的收敛速度和精度。将该算法应用于IEEE-14节点系统中,通过比较,结果表明了该模型和算法在解决多目标无功优化问题的优越性和实用性,为求解多目标无功优化问题,提供了一个新方法。

参考文献

[1]盛四清,李婧,田文树.群智能算法在电力系统无功优化中的应用[J].电力科学与工程,2008,24(1):1-4.

[2]马立新,单冠华,屈娜娜.基于改进粒子群算法的电力系统无功优化[J].控制工程,2012,19(6):1077-1080,1084.

[3]叶德意,何正友,臧天磊.基于自适应变异粒子群算法的分布式电源选址与容量确定[J].电网技术,2011,35(6):155-160.

[4]史丽萍,王攀攀,胡泳军,等.基于骨干微粒群算法和支持向量机的电机转子断条故障诊断[J].电工技术学报,2014,29(1):147-155.

[5]吕振肃,侯志荣.自适应变异的粒子群优化算法[J].电子学报,2004,32(3):416-420.

[6]马立新,王宏宇.基于非支配解的多目标粒子群无功优化[J].控制工程,2014,21(5):748-752.

[7]张伯明,陈寿孙,严正.高等电力网络分析[M].2版.北京:清华大学出版社,2007.

[8]冯士刚,艾芊.带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J].电工技术学报,2007,22(12):146-151.

[9]马立新,栾健,王继银.三目标柯西粒子群算法的电力系统无功优化[J].电子科技,2015,28(9):42-45.

Three-objective Adaptive Mutation Particle Swarm Optimizationfor Reactive Power Optimization

MA Lixin1,WANG Jiyin2,LUAN Jian3,HUANG Yanglong4

(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractPower system reactive power optimization is an important link in improving the power quality and ensuring the power grid to operate.This paper establishes a reactive power optimization model of considering minimization of loss and voltage deviation and maximum of voltage stability margin.The adaptive mutation particle swarm optimization is introduced for the three-objective reactive power optimization.This algorithm monitors particle group status of gathering dynamically by group fitness variance and adopts the method of adding random disturbance to vary gathered particles,using weight of inertia adaptive adjustment to jump out of local optimal and prevent premature,thus higher convergence speed and accuracy.The algorithm is implemented on the IEEE-14 bus system.Comparison with other algorithms shows the superiority and practicability of this model and algorithm in solving multi-objective power system reactive power optimization problems.

Keywordsparticle swarm optimization;mutation;three-objective;reactive power optimization;variance

中图分类号TP306.1

文献标识码A

文章编号1007-7820(2016)04-041-04

doi:10.16180/j.cnki.issn1007-7820.2016.04.011

作者简介:马立新(1960—),男,教授,博士,硕士生导师。研究方向:配电网规划与优化配置等。王继银(1987—),男,硕士研究生。研究方向:电力系统无功优化。

基金项目:沪江基金资助项目(C14002);上海市张江国家自主创新重点基金资助项目(201310-PI-B2-008)

收稿日期:2015- 09- 14