用分解运动巧解带电粒子在复合场中的运动

李鲁淼

摘 要：带电粒子在电磁场中的运动一般比较复杂，高中阶段能够定量处理的一般仅限于匀速直线运动与匀速圆周运动。其中，以与磁场垂直的速度进入匀强磁场做匀速圆周运动最为常见，圆周运动的半径R=。而处理曲线运动，基本方法是分解运动。以下就要借此方法，合理地分解运动，巧妙处理带电粒子在电磁场中复杂的曲线运动。

关键词：分解运动；轨迹；曲率半径

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2016）4-0045-4

1 带电粒子在磁场中运动

若初速度方向与磁场方向斜交，如图1所示，可以把v分解为与B垂直分量v⊥及与B平行分量v//。

v⊥=vsinθ，v//=vcosθ。

v⊥使带电粒子受洛伦兹力的作用，在垂直于B的平面上做匀速圆周运动，半径R和周期T分别为R=，T=。

v//使粒子平行于B的方向上做匀速直线运动，两个运动合成为等距螺旋线，螺距h= v//T。若以出发点为坐标原点O，B方向为z轴，圆周运动平面为xOy平面，圆周运动的角速度ω=Bq/m，其轨迹方程为：

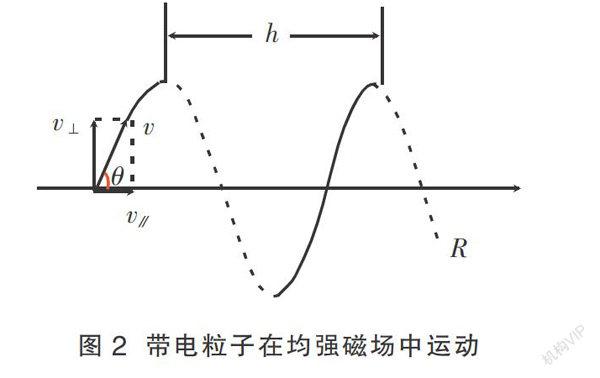
应用此结论可以求解一般等距螺旋运动的曲率半径。设轨道圆周运动半径为R，圆周运动周期为T，螺距为h，如图2所示。

如图3所示，若磁场方向沿y轴正方向，速度方向与xOz平面夹角为θ，仍可将速度分解，仍然以v//沿y轴匀速运动，以v⊥做匀速圆周运动，轨迹仍为等距螺旋线。

2 带电粒子在复合场中的运动

关于带电粒子在速度选择器中的运动规律，可总结为：

如图4，若电场强度为E，磁场强度为B，带电粒子的质量为m，电荷量为q，进入磁场时的速度为v，方向水平向右。

当速度v=时，向上的洛伦兹力与向下的电场力平衡，带电粒子做匀速直线运动，轨迹为Ⅰ。

当速度v<时，向上的洛伦兹力小于向下的电场力，带电粒子向下偏转，轨迹为Ⅱ。

当速度v>时，向上的洛伦兹力大于向下的电场力，带电粒子向上偏转，轨迹为Ⅲ。

下面来讨论轨迹Ⅱ、Ⅲ。借助轨迹Ⅰ的特点，可以把初速度v分解为v1与v2，其中，v1=，v2=v-v1，v1方向与v方向相同，其产生的洛伦兹力与电场力平衡，粒子以v1做匀速直线运动。同时，以v2为线速度在同一平面内做匀速圆周运动，粒子实际运动是由两个分运动合成，其轨迹是一个旋轮线。粒子运动具有周期性，竖直方向一个周期后回到原来的位置，粒子离开初速度方向垂直距离最大值d=2R=2。

①若初速度v<，则速度可以分解如图5所示， v1=方向水平向右；v2=v1-v，方向水平向左。粒子的轨迹为图5中的实曲线部分，最低点的速度方向水平向右，大小v1+v2。

当v1

2008年江苏卷第14题。在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O点静止释放，小球的运动曲线如图9所示。已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g。求：（1）小球运动到任意位置P（x，y）处的速率v；（2）小球在运动过程中第一次下降的最大距离ym。（3）当在上述磁场中加一竖直向上场强为E（E>）的匀强电场时，小球从O静止释放后获得的最大速率 vm。

其中，小球受到的重力充当原来的电场力，小球的出发点即为上述v1=v2情况的最高点。所以，可以假设小球出发时，存在两个大小相等、方向相反的速度，速度大小均为。其中，曲线在最低点的曲率半径为该点到x轴距离的2倍，即为此种情况的结论，其运动规律就与v1=v2情况相同了。

若初速度的方向与水平方向成θ，如图10所示。可以将速度v分解为v1与v2，其中由v1产生的安培力仍与电场力平衡，以v2为线速度做匀速圆周运动。若初速度的方向与纸面不共面，同样可以将速度分解为v1与v2，其中v1产生的洛伦兹力仍与电场力平衡，在此方向做匀速直线运动，而v2使粒子做等距的螺旋运动，粒子同时参与了这两个运动。

通过上述问题的探讨，告诉我们应该要善于利用已有知识来处理新的问题，既巩固和强化已有知识的体系，又加深对新知识的理解与应用，真正做到学以致用。

（栏目编辑 陈 洁）