预应力锚索抗滑桩锚固位置优化研究

邵 磊

预应力锚索抗滑桩锚固位置优化研究

邵 磊

(连云港职业技术学院建筑工程学院，江苏 连云港 222006)

以预应力锚索抗滑桩为研究对象，通过建立相应的数值模型研究预应力锚索在抗滑桩桩体上锚固位置的不同对边坡变形及支护结构的受力影响。结果表明：将锚固点从桩顶适当下移时，边坡位移没有明显变化，并可以提高边坡的稳定性，且当锚固点从桩顶下移至1.0～1.5 m时最为合适；将锚固点从桩顶适当下移与锚固于桩顶相比，支护结构内力有一定增加但未超过设计值且在可控范围内，但是锚固点适当下移时可有效避免抗滑桩桩身出现异号弯矩，对桩身的配筋设计较为有利。

预应力锚索；抗滑桩；锚固位置优化；边坡稳定性；数值模拟

预应力锚索抗滑桩在滑坡治理中已经得到了广泛的应用，抗滑桩为被动受力，预应力锚索为主动受力，两者结合之后能够有效地控制滑坡变形，因此在很多滑坡的处理中均采用此种桩锚支护结构[1-6]。

目前一些学者对桩锚支护结构在边坡治理中的应用进行了大量研究。如刘志勇等[7-9]通过工程实例分析了桩锚支护结构的有效性，认为与纯抗滑桩支护相比桩锚支护结构不仅能减少边坡位移，还能减少桩身内力；曹兴松等[10]研究了桩锚支护结构的设计计算方法，并与传统方法对比后，认为在桩锚支护结构设计时应该分阶段进行，即分为锚索张拉前和张拉后两个阶段，然后再进行内力及位移的叠加，从而得出了改进的桩锚支护结构设计计算方法与实测结果更为一致的结论；方理刚等[11]研究了桩锚支护结构加固边坡的作用机理，认为锚索改变了桩的受力机制，使之更为合理，同时更为有效地控制了滑坡的进一步发展；李世贵等[12]研究了预应力锚索抗滑桩的设计方法，对传统的方法进行了优化，改进后的设计方法能够节省钢筋用量，并可以提高设计的精度及工作效率。

综上分析可见，前人的研究主要集中在桩锚支护结构工程实例分析及设计方法上的探讨，而针对预应力锚索与抗滑桩的锚固位置研究甚少，传统的方法是将预应力锚索锚固于抗滑桩桩顶，但是笔者通过计算与分析发现，锚固位置位于桩顶并非最合理，针对这一问题，本文采用数值模拟的手段计算与分析了锚固位置不同的条件下边坡变形及支护结构的受力情况。

1 数值模型建立

本文研究对象为覆盖层滑坡，上部为覆盖层，中部为强风化层，下部为中风化层，岩土体物理力学参数见表1，滑坡体主要由上部覆盖层组成，桩锚支护结构位于坡体中下部，见图1。

表1 岩土体物理力学参数

图1 滑坡构成及支护结构位置Fig.1 Composition of the landslide and location of the supporting structure

根据覆盖层滑坡工程地质条件，采用FLAC3D模拟软件建立数值模型，见图2。为了消除边界效应，模型尺寸取100 m×45 m，模型边界均超出滑体15 m以上。为了计算的精确性，在网格划分时覆盖层及强风化层较中风化层要小，因为主要变形部位将集中于覆盖层和强风化层。

计算时岩土体本构模型为摩尔-库伦模型，模型底部采用全约束，即约束其水平及垂直方向的变形，模型两侧约束其水平向变形，模型顶部无约束。抗滑桩采用FLAC3D软件自带的结构单元Pile，抗滑桩深入底部中风化层1 m，长度为12 m，直径为1 m，桩身设计弯矩值为550 kN·m。预应力锚索采用Cable单元，锚索锚固角度为30°，锚固段长度为6 m，锚索采用5束7丝钢绞线，锚固段均位于边坡底部的中风化层中，施加的预应力值为300 kN。

图2 数值模型(单位：m)Fig.2 Numerical model(unit:m)

计算时分为5种工况，即锚索锚固点位置分别位于桩顶以下0 m、0.5 m、1.0 m、1.5 m、2.0 m，分别对应于工况1～5，本文主要分析不同工况下边坡的位移及支护结构的内力分布情况。

2 数值模拟计算结果与分析

2.1 支护前后边坡位移分布情况

支护前边坡位移分布情况见图3。由图3可见，边坡最大水平位移X为145.81 mm，位于坡体中部，最大垂直位移Y为83.25 mm，位于坡顶。边坡稳定性系数计算结果为1.003，表明边坡处于临界状态。

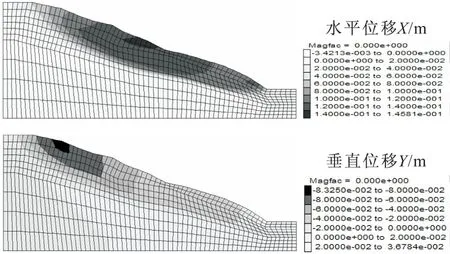
图3 支护前边坡位移分布情况Fig.3 Distribution of slope displacements before supporting

支护后的边坡位移分布情况见图4，为工况1即锚索锚固于桩顶的数值模拟与计算结果。由图4可见，边坡最大水平位移为28.34 mm，位于坡体中上部，支护结构有效地控制了滑坡的移动；边坡最大垂直位移Y为18.834 mm，位于坡顶。边坡稳定性系数计算结果为1.214，说明预应力锚索抗滑桩支护效果良好。其余工况所得规律与工况类似，因此不再赘述。

图4 支护后边坡位移分布情况Fig.4 Distribution of slope displacements after supporting

2.2 各工况边坡稳定性对比

各工况边坡最大位移对比情况见图5。由图5可见，当锚索锚固点从桩顶改变至桩顶以下0.5 m、1.0 m及1.5 m时，边坡的位移改变较小；而当锚索锚固点位置移至桩顶下2 m时，边坡位移突然变大，边坡最大水平位移增大至68.516 mm，边坡最大垂直位移增大至35.026 mm，说明锚索锚固点离桩顶较远时，边坡的位移无法有效地得到控制，这是由于在锚固点上方，桩体没有得到约束，相当于纯抗滑桩支护结构。

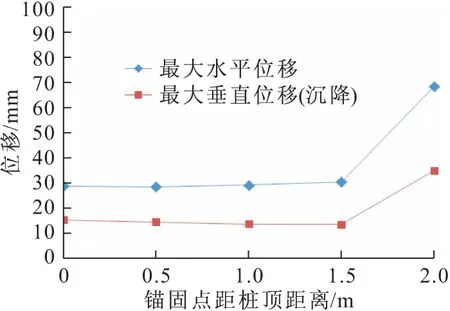
图5 各工况边坡最大位移对比Fig.5 Contrast of maximum slope displacements under each condition

各工况边坡稳定性计算结果对比见图6。由图6可见，当锚索锚固点位置下移在1.5 m范围内时，边坡的稳定性系数没有下降，反而得到不同程度的提升，仅当锚索锚固点位置下移至2 m时边坡稳定性系数明显下降，这一点从图6中的剪应变增量变化趋势也可以看出，当锚索锚固点位置下移在1.5 m范围内时，边坡的最大剪应变增量逐渐降低，当其下移至2 m时，边坡的最大剪应变增量突然增大，这说明将锚索的锚固点位移适当下移能够更为有效地阻挡边坡的滑动。

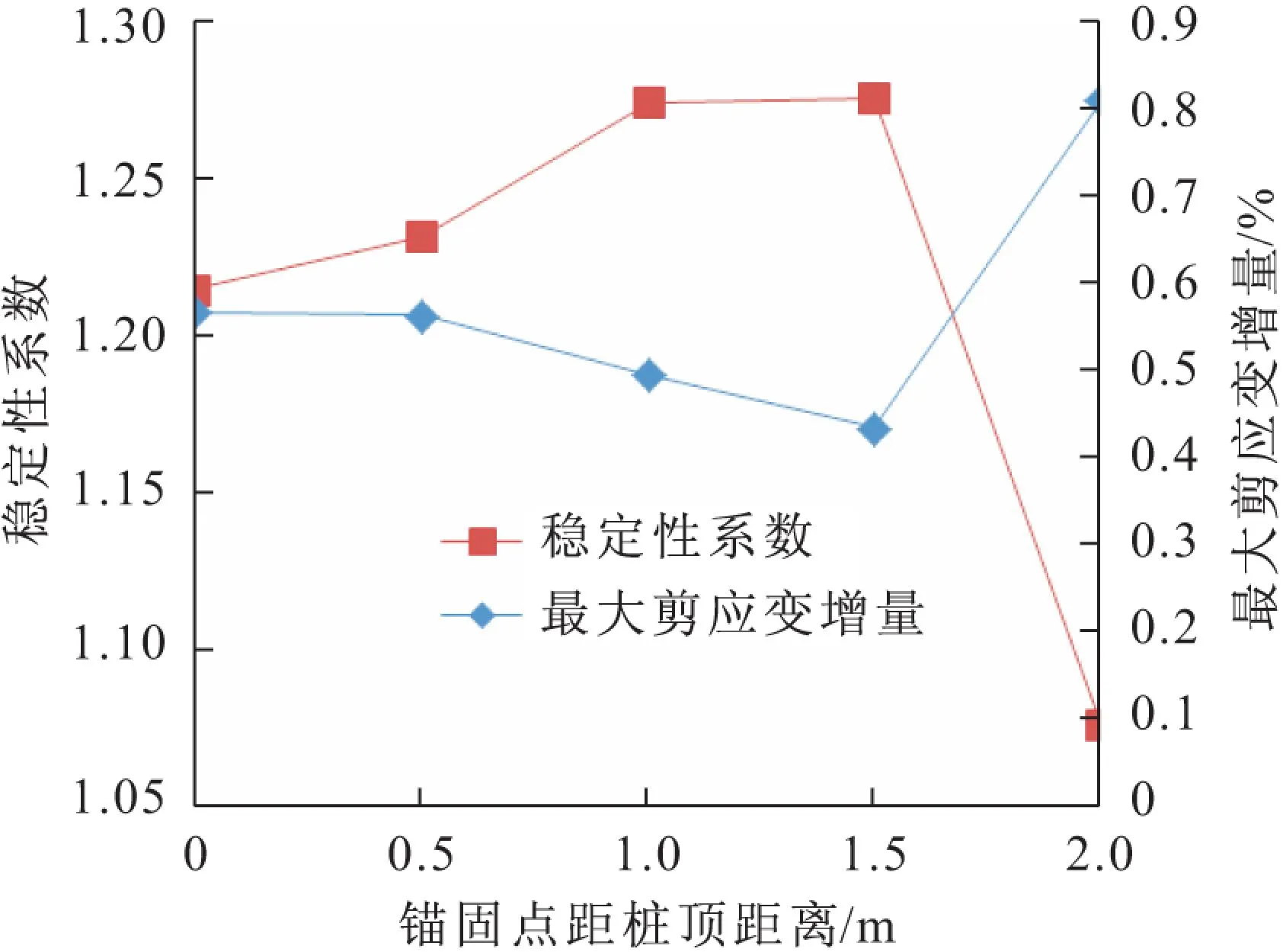
图6 各工况边坡稳定性对比Fig.6 Comparison of slope stability under each condition

2.3 支护结构内力对比

各工况下抗滑桩桩身弯矩分布情况见图7。由图7可见，桩身分布有正弯矩亦有负弯矩，最大正弯矩位于桩底，最大负弯矩位于桩身中上部，桩顶弯矩为0。这与纯抗滑桩支护时有区别，一般情况下，纯抗滑桩支护时，抗滑桩相当于一悬臂结构，桩身不存在异号弯矩；但是在预应力抗滑桩支护结构中，由于桩顶受到了锚索的拉力，即桩身受到了两个方向的作用力，因此存在异号弯矩。

图7 各工况抗滑桩桩身弯矩分布情况Fig.7 Distribution of bending moments of the stabilizing piles under each condition

各工况预应力锚索的轴力对比见图8。由图8可见，各工况预应力锚索的轴力分布规律一致，锚索自由段轴力均为直线分布即大小相同，进入锚固段之后轴力逐渐减小至0，且其分布规律与实际情况是吻合的，说明锚索相关参数设置是合理的，而锚固段末段轴力为0，说明锚索处于正常工作状态。

图8 各工况预应力锚索轴力分布情况Fig.8 Distribution of axial forces of the prestressed anchor under each condition

为了更清晰地对比各工况支护结构的内力分布情况，本文将抗滑桩桩身正弯矩及负弯矩、桩身弯矩反弯点位置、锚索轴力单独提出来进行对比，图9为各工况抗滑桩桩身最大正弯矩与锚索最大轴力对比图，图10为各工况抗滑桩桩身最大负弯矩与桩身弯矩反弯点位置的对比图。

图9 各工况桩身弯矩与锚索轴力对比图Fig.9 Contrast of bending moments of the pile and axial forces of the anchor under each condition

由图9可见，抗滑桩桩身弯矩与锚索轴力变化规律较一致，锚固点位置从桩顶变化至桩顶以下1.5 m时，桩身弯矩及锚索轴力逐渐增大，锚固点位置移至桩顶下2.0 m时，桩身弯矩及锚索轴力突然下降。其中，在锚固点位于桩顶下1.0 m及1.5 m时桩身弯矩达较大值，分别为299.4 kN·m、320.5 kN·m，但离桩身弯矩设计值仍有较大空间，说明抗滑桩桩身强度仍有较大的安全储备。从锚索轴力来看，其变化规律与上述相同，在锚固点分别位于桩顶下1.0 m及1.5 m时锚索轴力达较大值，分别为387.4 kN、378.1 kN。

结合上述边坡稳定性计算结果可以看出，锚固点适当下移时边坡稳定性得到了增加，而支护结构内力计算结果显示，边坡稳定性增加的同时，支护结构的内力也同样增加，但是离内力设计值仍有较大余地，说明支护结构受力不存在隐患。因此，可以认为预应力锚索的锚固点适当下移可以更为充分地发挥支护结构的作用，提高边坡的稳定性。这一点可以从锚固点位于桩顶以下2.0 m时的计算结果中得到验证，该工况支护结构内力最小，锚索轴力甚至小于预应力值，而其稳定性在各工况中也是最小的。

图10 各工况桩身负弯矩与桩身弯矩反弯点位置对比图Fig.10 Contrast of negative bending moments and inflection point location of the pile under each condition

由图10可见，桩身最大负弯矩与桩身弯矩反弯点位置变化规律较一致，锚固点位于桩顶时桩身有一定的负弯矩，最大值为29.4 kN·m，当锚固点位于桩顶以下0.5 m、1.0 m及1.5 m时，桩身负弯矩几乎为0，说明锚固点位置适当下移能够有效避免桩身产生异号弯矩，更有利于桩身的配筋设计。

3 结 论

通过数值模拟方法研究了预应力锚索在抗滑桩桩体上锚固位置的不同对边坡稳定性的影响，得到如下结论：

(1) 当锚固点从桩顶适当下移时，边坡的水平向及垂直向位移变化并不明显，仅当锚固点下移至桩顶以下2.0m时边坡位移有较大的增加。

(2) 从边坡稳定性计算结果来看，锚固点适当下移时边坡稳定性得到了提高，但是锚固点下移过大时则效果相反。通过本文假定的工况计算结果来看，锚固点从桩顶下移1.0～1.5 m最为合适。

(3) 抗滑桩在锚索及基岩的作用下桩身存在异号弯矩，但是当锚固点适当下移时，桩身异号弯矩几乎为0，这一规律在桩锚支护结构设计中值得参考。

[1] 张歆瑜.锚索框架梁结合锚索抗滑桩在港区陆域山体边坡加固中的应用[J].水运工程,2013(10):40-46.

[2] 张涛,门玉明,石胜伟等.悬臂式单锚抗滑桩加固黄土滑坡的模型试验[J].安全与环境工程,2015(3):.151-157.

[3] 秦凤艳,戈海玉.某滑坡支护方案的比选及优化[J].水利水电科技进展,2014(3):70-74.

[4] 万飞,邓清禄,张申,等.基于BOTDA的光纤传感技术在抗滑桩变形监测中的应用[J].安全与环境工程,2014(3):36-40，45.

[5] 叶银英.路堑高边坡稳定性实例分析及治理[J].铁道建筑,2014(8):69-72.

[6] 刘志勇,黄伟伟,吴仁铣.煤系地层路基边坡锚索抗滑桩加固作用机理分析研究[J].公路工程,2012(4):92-95.

[7] 田小波.预应力锚索抗滑桩优化设计及应用[J].铁道科学与工程学报,2012(4):89-93.

[8] 柳治国,谭捍华,张家新.锚索与抗滑桩在顺层岩质边坡治理中的应用[J].公路工程,2008(3):14-17，42.

[9] 刘庆涛,李长冬,谷飞宏,等.抗滑桩细观受力特征的数值模拟研究[J].安全与环境工程,2012(4):22-26.

[10]曹兴松,周德培.软岩高边坡预应力锚索抗滑桩的设计计算[J].山地学报,2005(4):4447-4452.

[11]方理刚,孙正兵,王强.桩锚加固边坡的作用机理和稳定性分析研究[J].公路工程,2007(4):152-155，166.

[12]李世贵,任仁,朱大权,等.预应力锚索抗滑桩设计方法优化研究[J].公路工程,2013(2):51-54.

Optimization of Anchoring Position of the Prestressed Anchor Stabilizing Pile

SHAO Lei

(DepartmentofArchitecturalEngineering,LianyungangTechnicalCollege,Lianyungang222006,China)

Taking the prestressed anchor stabilizing pile as the research object,this paper explores the effects of different anchoring positions of the prestressed anchor stabilizing pile on deformation of the slope and stress of the supporting structure by establishing the corresponding numerical models.The results show that:when the anchoring point moves down from the top of the pile appropriately,the displacement of slope does not change significantly,and it can improve the stability of slope with the optimal anchoring position being 1.0～1.5 m that is moved from below the top of the pile.Compared with the anchoring position being on top of the pile,the internal force of supporting structure increases in some extent but not exceeding the design value if the anchor point moves down from the top of the pile,and it is within the controllable range.However,moving down the anchor point appropriately can effectively avoid the opposite-sign moments of the pile,which is more favorable to reinforcement design of the pile.

prestressed anchor;stabilizing pile;optimization of anchoring position;slope stability;numerical simulation

鲁长波(1975—)，男，博士，高级工程师，主要从事军用燃料方面的研究工作。 E-mail:18600209811@vip.163.com

1671-1556(2016)02-0143-04

2015-07-08

2015-12-08

邵 磊(1965—)，男，硕士，讲师，主要从事工程管理方面的教学与科研工作。E-mail：lygshaolei2015@163.com

X93；P642.22

A

10.13578/j.cnki.issn.1671-1556.2016.02.026