古墓垂直防渗帷幕安全深度的优化设计

王日冉，马清文,2

古墓垂直防渗帷幕安全深度的优化设计

王日冉1，马清文1,2

(1.郑州大学水利与环境学院，河南 郑州 450001；2.水利与交通基础设施安全防护

河南省协同创新中心，河南 郑州 450001)

古墓作为特殊的文物保护群体，在实施保护时尤其要注意原状维护和病害防治。地下水渗漏问题已经发展成为古墓最主要的病害之一，目前的治理方法主要是在古墓周边布置垂直防渗帷幕，形成不透水地下连续墙。对防渗帷幕的安全深度进行优化设计成为解决影响防渗效果和工程造价问题的关键。结合地下水渗流理论，分析防渗帷幕深度的主要影响因素，以墓室底部土体不发生渗透破坏为控制条件计算垂直防渗帷幕插入深度，并通过工程实例利用ANSYS软件模拟地下水渗流场，对理论计算结果进行验证。结果表明：理论计算得出的古墓垂直防渗帷幕安全深度是可靠的，且满足刘崇墓古墓的防渗保护要求。

古墓；垂直防渗帷幕；安全深度；渗流场

大型墓葬遗址的真实性和不可再生性决定了保护工作的迫切性与科学性。经过走访、调研及查阅历史文献资料发现，在已经发掘的国家级及省级古墓葬中存在大量地表、地下水渗漏和结构破坏问题，如果任其发展，长此下去便会给文物带来极大的安全隐患。由于墓葬大都是地下洞室，古墓的渗水来源主要以墓地周边地表及地下水渗流为主，雨后渗水更多。该问题类似于工程上常见的基坑渗水问题，不同之处就是在治理时要遵循不改变文物原状和减少人为干预的原则。目前主要采用疏、堵、排的治理方法，在墓室周边建立封闭的垂直防渗帷幕，形成不透水地下连续墙，用来减少渗流量和降低渗流速度，以达到保护墓室的目的。

目前对于地下防渗墙及其覆盖层的渗透稳定问题已有一些研究成果。如毛昶熙等[1]在实验室水槽中进行了悬挂式防渗墙的砂质堤基的渗流模型管涌试验，确定了悬挂式防渗墙及其前后水平段的渗流临界坡降，并进行了相关的理论分析;沈振中等[2]提出了悬挂式混凝土防渗墙深度优化设计方案;张家发等[3]通过砂槽模型模拟了渗透变形发生和扩展的过程，指出悬挂式防渗墙对渗透变形的发生条件影响很小;谢兴华等[4]对深厚覆盖层坝基防渗墙最优深度进行了研究,并指出最优深度的取值取决于覆盖层的深度;杨波等[5]考虑防渗帷幕强度和弹性模量值对超深防渗帷幕的影响而进行优化设计，同时以基坑降水深度和允许渗透坡降来确定防渗帷幕厚度;宋永占等[6]采用了Fluent数值模拟程序对防渗帷幕在不同贯入深度的工况下进行分析,从而得到了防渗帷幕深度合理值；李建华等[7]根据边界元的特点和计算理论，分析了防渗墙位置和深度对渗流量的影响；杨秀竹等[8]结合工程实例说明悬挂式防渗帷幕在建造前后防渗效果显著，并指出悬挂式防渗帷幕底部小范围内需要提高抗冲刷能力；徐书平等[9]实现了渗流分析边界条件处理的新算法；孙庆春等[10]提出的修复地下水重金属污染的渗透反应墙技术对土遗址地下水环境保护具有借鉴意义；陈义等[11]应用ANSYS对裂隙全充填的岩体进行了数值模拟计算，该研究对于古墓地下防渗墙体的数值模拟具有参考价值。总之，防渗问题一直以来是土木工程和水利工程领域内的重大问题，且防渗技术与许多工程实践密切相关。由于渗流而产生的工程问题主要有两大类：渗透变形问题和渗流量与渗流速率的问题，本文结合这两方面问题和上述在防渗工程中对防渗帷幕设计方面的研究，主要考虑墓区土层参数和地下水位特征等因素，对古墓防渗帷幕安全深度进行了优化设计。

1 地下水渗流理论及防渗帷幕安全深度影响因素

1.1 二维稳定渗流的基本方程

在研究各向同性土体的二维稳定渗流基本方程的建立方法时，假定从稳定渗流场中任取一微小的土单元体，在渗流作用下单元体的体积保持不变且水不可压缩，单位时间内流入单元体的总水量等于流出的总水量，根据达西定律和连续性方程有：

(1)

式中:k为土体渗透系数(m/s)；h为总水头或测压管水头(m)。

式(1)化简后为

(2)

式(2)即为各向同性土体二维稳定渗流的基本方程式，也就是著名的拉普拉斯(Laplace)方程。渗流速度的分量为

1.2 有限元方程

二维稳定渗流属于带直边界条件的问题，可以采用线性形函数近似独立变量的方法来解决地下水渗流水头的空间变化问题。现对二维稳定渗流问题采用加重余差的迦辽金(Galerkin)有限元方法分析[12]，表征的基本方程为

(∫V[B]T[D][B]dA){H}=q∫A[N]TdL

(3)

式中：[B]为单元坡降矩阵；[D]为单元渗透系数矩阵；[N]为单元形函数矩阵；{H}为水头列阵；q为单元边界单宽流量；dL和dA分别为长度积分变量和面积积分变量；V为渗流区域体积；A为渗流过流面积。

将式(3)进一步化简，得

[K]{H}={Q}

(4)

式中:[K]表示单元渗透矩阵,[K]=∫V[B]T[D][B]dA;{Q}表示单元边界流量列阵,{Q}=q∫A[N]TdL。

分析地下水渗流理论，探究影响防渗帷幕安全深度的主要因素，是古墓防渗帷幕优化设计的关键。

1.3 影响防渗帷幕安全深度的主要因素

1.3.1 土层信息

多数古墓地下埋深较大，墓冢及墓室边墙周边填土土质松软，且杂草、灌木恣意生长，根系纵横交错，造成土层渗透性的增加，另外土质墓室的墓道通常以夯土为地基，夯土因自然力作用分化，加剧墓室渗水。因此，土层信息对于古墓地下水防渗至关重要。古墓防渗帷幕的防渗效果与帷幕的深度、厚度、位置因素有关，而关键因素是防渗帷幕的安全深度。帷幕的防渗作用对土层的渗透系数和帷幕本身的渗透性很敏感，当古墓防渗帷幕采用不透水材料时，帷幕本身的渗透性可以忽略，所以土层信息成为影响防渗帷幕安全深度的关键因素之一，原因是土层信息直接影响渗透系数的大小，如土的粒度成分、密实度、饱和度、结构和构造等信息。实际工程中的天然沉积土往往由渗透性不同的土层组成，对于与土层平行和垂直的渗流情况，当各个土层的渗透性和厚度为已知时，据此可以衡量整个土层的渗透性。

1.3.2 地下水位特征

多数古墓在发掘之前长期处在水量丰富的地下环境中，墓墙已严重老化，多处存在酥碱、剥蚀破坏，墓底地砖酥软破碎，已基本丧失防水功能。因此，地下水位特征是影响防渗帷幕安全深度的另一个重要因素，原因是地下水位直接决定水头的大小，而水头差是渗流发生的必要条件。

1.3.3 不透水层埋深

根据古墓地基不透水层埋深情况，并根据实际需要，垂直防渗帷幕可完全切断地基的透水层，深入到不透水层中，彻底解决地基土的渗透变形问题，也可不完全切断透水层，做成悬挂式防渗帷幕，起到延长渗流途径、降低下游的逸出坡降的作用；当相对不透水层埋深大且无规律时，应根据渗透分析及防渗要求并结合工程经验决定防渗帷幕的安全深度。

2 工程实例分析

2.1 工程概况

河南省周口市淮阳县刘崇墓遗址是一座东汉中期的大型砖石墓葬，古墓东西长28.3 m，南北宽18.2 m，墓室底深5.26 m，总面积为515 m2，2013年5月公布为第七批全国重点文物保护单位。由于地下水位上升，古墓墓室内产生严重渗水病害，长期的渗水导致墓顶、墓壁遭到严重的溶蚀，墓道积水导致墓砖严重破坏等问题。为截断渗流途径，降低渗流速度，减少渗流量，在古墓东侧1.5 m、西侧6 m、南侧6 m、北侧6 m处设置一道地下连续防渗墙，墙厚20 cm，采用超薄型高聚物防渗材料，整体形成“口”字形防渗墙。经勘察，近5年最高水位相对高程为-3.00 m左右，而该古墓的基础埋深为5.26 m，地下水类型基本为孔隙型潜水。依据地勘资料，土层自上而下分为：①素填土、②粉土、③黏土、④粉质黏土、⑤黏土。土层参数信息见表1。

表1 土层参数信息表

2.2 防渗帷幕插入深度分析

垂直防渗帷幕插人基坑开挖高程以下深度是影响防渗效果和工程造价的一个重要因素。经调研发现，刘崇墓墓室内地面有局部隆起现象，地面砖块被顶起，说明流土现象存在,因此在满足墓室结构稳定的前提下，古墓周围防渗帷幕安全插入深度的确定是以使得墓室底部土体不发生流土为控制条件来进行分析的。此外，防渗帷幕的最终安全深度要经过试算确定，鉴于粉质黏土层等弱透水层厚度较大，可以设置悬挂式竖向防渗帷幕来阻隔地下水。如图1所示，当墓室外的水绕过防渗帷幕向墓室底部渗透时，只有当渗透坡降i≤[i]([i]为墓室底部土体的允许渗透坡降)时，墓室底部土体才不会发生渗透破坏。

图1 防渗帷幕插入深度分析剖面图Fig.1 Cross-section of the insert depth analysis of anti-seepage curtain

计算土体渗透坡降时，应选择紧贴帷幕的最短渗径计算，此处的渗透坡降将最大，只要紧贴防渗帷幕内侧的土体不发生流土，便可认为墓室底部土体不会遭到渗透破坏。其计算公式如下：

(5)

式中:i为水力坡降(m)；d为墓室底部以下防渗帷幕深度(m)；d+5.26为防渗帷幕的总插人深度(m)；b为防渗帷幕的宽度(m),b=0.2 m；h为地下水位至墓室地面的距离(m)，h=5.26-3=2.26 m;[i]为允许渗透坡降(m)，结合《工程地质手册》和工程实践经验[i]取0.3。

因此，防渗帷幕的插入深度为

(6)

将各数据代入(6)式计算得d≫2.53 m,考虑古墓保护工程的重要性和特殊性，计算防渗帷幕的总插入深度时取安全系数为1.5，即防渗帷幕的总插入深度为(2.53+5.08)×1.5=11.42 m，综合考虑取为12 m，即深入到粉质黏土弱透水层，形成悬挂式防渗帷幕。

2.3 ANSYS渗流分析

ANSYS软件具有强大的分析功能，能够模拟分析自然界中的应力场、电磁场、温度场和流场，并且支持多场耦合分析。ANSYS软件提供了大量的单元用于流体力学问题的模型分析，这些单元包括FLUID15、FLUID66、FLUID79，由于各控制方程的相似性，除了上述几种单元外，还可以用热实体单元中6节点的三角形单元PLAIN35、4节点的四边形单元PLAIN55和8节点的四边形单元PLAIN77，本文采用8节点Solid单元PLAIN77来模拟分析地下渗流问题[13]。渗流分析时有以下三点主要假设：将渗流问题简化为平面问题；防渗墙采用不透水的防渗材料；地下水位作为渗透的唯一因素。

对于典型的稳定渗流问题，将已知的固定水位边界作为水头边界，另外还有出渗边界和防渗墙边界，在求解时没有给出边界条件的区域边界默认是不透水的，对应于渗流控制方程中的自然边界条件。液面水头通常是已知的，分析时将已知水头作为确定的边界条件。假定渗流是发生在各向同性土体内的二维稳定流,将地下水位边界和墓室底部渗流渗出处作为第一类边界条件；将墓室底部相对不透水的黏土层和防渗帷幕及四周不透水的周围介质作为第二类边界条件。在仿真分析时，选取靠近墓室边墙一侧的防渗帷幕进行模拟，具体边界尺寸如图2所示。

图2 地下水渗流场边界条件Fig.2 Boundary conditions of the groundwater seepage field

本文利用ANSYS软件，在防渗帷幕深度拟定的情况下，对地下水渗流场进行分析。考虑到渗流场被简化成了规则图形，在网格划分时采用自由划分，设置单元长度为0.4 m，在应力可能集中的部位进行了细化，设置单元长度为0.2 m，共划分1 550个单元，网格剖分结果见图3。土壤中渗流速度矢量分布见图4，沿路径A-B上渗流速度的变化见图5。

图3 网格剖分图Fig.3 Grid subdivision graph

图4 土壤中渗流速度的矢量分布Fig.4 Distribution of the vectors of seepage velocity in the soil

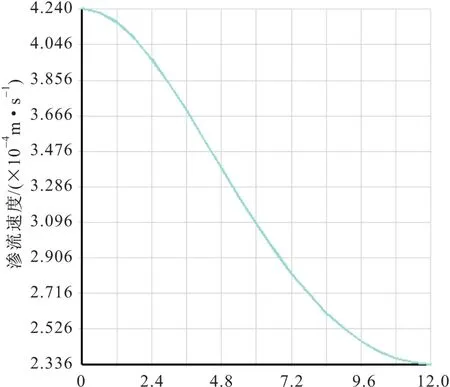
图5 沿路径A-B上渗流速度的变化Fig.5 Change of the seepage velocity along the path of A-B

由图4可见，最大渗流流速分布在防渗帷幕底部，其值为0.002 788 m/s，最小渗流流速为0.999×10-5m/s，其值非常小，即使在最不利情况下，一定时间内的渗透量也是非常有限的。另外，由图5可见，渗流流速在A点最大，其值为4.24×10-4m/s，并沿路径A-B下降，在B点渗流流速降为零，最后达到自由流体状态。依据渗流理论，A点附近的渗流流速要比B点渗流流速大，原因是A点对水流有较低的阻力，在A点附近有更多的水流经过。因此，此次有限元分析结果验证了理论解的可靠性，从而说明了设置12 m安全深度的防渗帷幕可满足古墓防渗的要求。

3 结 论

古墓保护工作的特殊性决定了防渗工作的特殊性，因此防渗设计必须科学严谨，工程处理更要做到周全到位，只有这样才能真正达到保护古墓的目的。本文在介绍各向同性土体二维稳定地下水渗流基本规律的基础上，采用加重余差的迦辽金法的有限元方程进一步分析了影响防渗帷幕安全深度的主要因素，并以墓室底部土体的允许渗透坡降为控制因素计算出防渗帷幕的插入深度，最后通过工程实例利用ANSYS软件模拟的渗流场对理论计算结果进行了验证。结果表明：理论计算出的防渗帷幕安全深度是可靠的，且满足刘崇墓的防渗保护要求。因此，本文提出的方法对形成专门针对古墓等特殊土遗址群完整而科学的防渗治理措施具有一定的参考价值。

[1] 毛昶熙，段祥宝，蔡金傍，等.悬挂式防渗墙控制管涌发展的试验研究[J].水利学报,2005,36(1):42-50.

[2] 沈振中,张鑫,陆希,等.西藏老虎嘴水电站左岸渗流控制优化[J].水利学报，2006，37(10)：1230-1234.

[3] 张家发，吴昌瑜，朱国胜.堤基渗透变形扩展过程及悬挂式防渗墙控制作用的试验模拟[J].水利学报，2002(9)：108-111，116.

[4] 谢兴华，王国庆.深厚覆盖层坝基防渗墙深度研究[J].岩土力学，2009,30(9)：2708-2712.

[5] 杨波，刘国彬，杨光煦.超深防渗帷幕性质研究及设计优化[J].岩土工程技术,2004,18(5):267-270.

[6] 宋永占，赵廷红，丁睿，等.混凝土重力坝坝基防渗帷幕作用的单因素分析[J].兰州理工大学学报，2011,37(6)：120-125.

[7] 李建华，侍克斌，王建祥.土石坝防渗墙位置和深度对渗流量的影响[J].河北工程大学学报，2009，26(2)：36-38.

[8] 杨秀竹，陈福全，雷金山，等.悬挂式帷幕防渗作用的有限元模拟[J].岩土力学，2005,26(1)：105-107.

[9] 徐书平，喻国安，杨剑飞.渗流分析边界条件处理的算法实现[J].土工基础，2002,16(2):51-53.

[10]孙庆春，崔康平，许为义,等.重金属污染地下水修复的渗透反应墙技术[J].安全与环境工程，2013,20(5):53-56.

[11]陈义，王传琪，陈金刚.基于ANSYS的裂隙岩体全充填介质膨胀效应的数值模拟[J].安全与环境工程，2012,19(4)：115-118，128.

[12]潘荣升.高压喷射注浆防渗帷幕防渗机理及其应用研究[D].长沙：中南大学，2012.

[13]Saeed Moaveni.有限元分析—ANSYS理论与应用[M].王崧等译.2版.北京：电子工业出版社，2005.

Optimal Design about the Safety Depth of Vertical Anti-seepage Curtain in Ancient Tombs

WANG Riran1，MA Qingwen1,2

(1.SchoolofWaterConservancyandEnvironment,ZhengzhouUniversity，Zhengzhou450001，China；2.CollaborativeInnovationCenterofWaterConservancyandTransportationInfrastructureSafetyProtectionofHenanProvince，Zhengzhou450001，China)

Ancient tombs are a special group of cultural relics,of which the original state maintenance and disease control should be paid more attention to.Groundwater seepage problem has become one of the main diseases,and the treatment at present is mainly arrangement of vertical anti-seepage curtain aimed at forming impermeable underground continuous wall.To obtain the optimal design of the safety depth of the anti-seepage curtain becomes the key to solving the problem of seepage control effect and engineering cost.Combined with the groundwater seepage theory,this paper analyzes the main influencing factors of anti-seepage curtain depth,and calculates the safety depth of the vertical anti-seepage curtain by taking the nonoccurrence of the seepage failure as a control condition,and also testifies the theoretical calculation results by adopting the ANSYS software to simulate the groundwater seepage field through a project case study.The results indicate that the theoretical calculation of the safety depth of vertical anti-seepage curtain is reliable,which satisfies the requirements of the anti-seepage prevention of ancient Liuchong tombs.

ancient tomb;vertical anti-seepage curtain;safety depth;seepage field

1671-1556(2016)02-0125-05

2015-07-07

2015-11-20

河南省科技攻关项目(142102210071)

王日冉(1990—)，女，硕士研究生，主要研究方向为水利与交通基础设施安全防护等。E-mail：wangriran23409708@163.com

X93;TU761.1+1

A

10.13578/j.cnki.issn.1671-1556.2016.02.023